
A POMDP-based Camera Selection Method
Li Qian
1,2
, Sun Zheng-Xing
1
, and Chen Song-Le
1
1
State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing 210093, China
2
Institute of Meteorology, PLA University of Science and Technology, Nanjing 211101, China
Keywords: Camera Selection, POMDP, Video Analysis, Multi-camera System.
Abstract: This paper addresses the problem of camera selection in multi-camera systems and proposes a novel
selection method based on a partially observable Markov decision process model (POMDP). And an
innovative evaluation function identifies the most informative of several multi-view video streams by
extracting and scoring features related to global motion, attributes of moving objects, and special events
such as the appearance of new objects. The experiments show that these proposed visual evaluation criteria
successfully measure changes in scenes and our camera selection method effectively reduces camera
switching.
1 INTRODUCTION
Multiple cameras are widely used for security
surveillance, human–computer interaction,
navigation, and positioning. However, they
introduce issues related to deployment and control
the cameras, real-time fusion of video streams with
high resolution and high frame rates, and selection
and coordination of the cameras (Soro and
Heinzelman, 2009). Camera selection, which
involves selection of one or more cameras from a
group of cameras to extract essential information, is
a particularly challenging task in multi-camera
systems.
A number of previous studies have investigated
the issues related to camera selection. Li and Bhanu
(Li and Bhanu, 2009) proposed a game-theoretic
approach to hand-off the camera with the global
utility, camera utility, and person utility determined
by user-supplied criteria such as the size, position,
and view of the individual being tracked. Daniyal,
Taj, and Cavallaro (Daniyal et al., 2010) proposed a
Dynamic Bayesian Network approach that uses
object- and frame-level features. Bimbo and Pernici
(Bimbo and Pernici, 2006) selected optimal
parameters for the active camera on the basis of the
appearance of objects and predicted motions to solve
the traveling salesman problem. Tessens et. al
(Tessens et al., 2008) used face detection and the
calculated spatial position of the target to select a
primary view and a number of additional views. All
methods mentioned above use low-level image
features to evaluate visual information; high-level
information in video streams, such as local salient
movement details and specific events, is more
informative.
In this paper, we present a novel method for
camera selection based on a partially observable
Markov decision model (POMDP) and use the belief
states of the model to represent noisy visual
information. By considering current states and
anticipated transition trends with the cost generated
by camera switching, the visual jitters that arise from
frequent switching can be effectively reduced. Our
evaluation function are presented for visual
information, which is designed to reflect the richness
of information in each view by extracting global
motion, properties of moving objects in the scene,
and specific events.
2 DYNAMIC CAMERA
SELECTION BASED ON A
POMDP MODEL
The camera selection problem can be described as
follows. A multi-camera system has
N
cameras
12
( , ,... )
N
CC C
with partially or completely
overlapped FOVs, and one node is designated as the
central controller for scheduling according to a
selection policy that is computed offline. In our
746
Qian L., Zheng-Xing S. and Song-Le C..
A POMDP-based Camera Selection Method .
DOI: 10.5220/0004228907460751
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 746-751
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

method, the central controller selects only one
camera
*
C
online as the optimal camera at fixed
time intervals of duration
t
. At each time step
t
,
visual features indicating global motion, properties
of objects, and specific events in the view of each
camera are extracted and scored (see Section 3). The
scores are then sent to the central controller, which
makes dynamic selection decisions based on current
and previous camera view scores. Although the
camera selection problem can usually be modeled as
a finite-state Markov decision process (MDP), when
an observed state contains errors caused by factors
such as illumination, occlusion, and camera shock
and does not reflect the actual state, we must
implement sequential decision making based on
partially observable states. Owing to uncertainty, we
model this dynamic process as a POMDP, which is
an extended version of an MDP.
2.1 Definition of POMDPs
A POMDP can be formally defined as a 6-
tuple
,,,,,SA TOR
, where
S
is a finite set of
all possible underlying states,
A
is a finite set of
actions, i.e., available control choices at each time
instant,
is a finite set of all possible observations
that the process can provide,
T
is a state transition
function
:TSA S
that encodes the uncertainty
about the evolution of the states of the process,
O
is
an observation function
:OS A
that relates
the process outputs (camera observations) to the true
underlying state of the process, and
R
is an
immediate reward function
:RSAR
that
assigns real-valued rewards to the actions that may
be performed in each of the underlying process
states.
2.2 Selection Policy
On the basis of our description of the camera
selection problem, we formulate the POMDP as
follows.
1)
System state vector
The system state vector consists of the currently
selected results and visual information scores. At
time step
t
, the system state is represented as
12
[ , , ,..., ]
iN
tttt t
Scss s
, where
i
t
c
is the best camera
i
that is selected at time
t
, and
, {1, 2,..., }
k
t
s
kN
is
the actual visual information score for camera
k
.
And the score values
k
t
s
are uniformly discretized
with
m
quantization levels and normalized to [0,1]
to produce the range
{0,1, ..., 1}
k
t
sm
.
2)
Actions
An action is a vector represented as
1
[ ,..., ]
N
tt t
aa a
, where at time step
t
if the
i
th
camera is selected,
1
i
t
a
; else
0
i
t
a
.
3)
Observation state
The observation state is a collection of
observations from all cameras and is defined as the
vector
12
[', , ,..., ]
iN
ttttt
Ocoo o
.
'
i
t
c
is the camera
i
that is selected at time
t
. Because this component
has no error, it should be the same as the component
i
t
c
of the system state, which is similar to the
definition of system states. Each
observation
, {1, 2,..., }
k
t
ok N
is the visual score
computed by our method for camera
k
at time step
t
obtained by extracting visual features from the
video stream and scoring them. The number of
observations is equal to the number of system states.
4)
State transitions
The state transition probability
'|
s
as
p
describes
the differences in the scene between the views taken
in adjacent time steps. Because the selection action
does not affect the visual measures and state
transitions
'| '|
s
as s s
pp
, the state transition will be
based on the visual score component
k
t
s
. We assume
that the visual scores for the cameras are
independent, i.e.,
12 12
11 1
11 22
11 1
Pr( ' ( , ,..., ) | ( , ,..., ))
Pr( | ) Pr( | ) ... Pr( | )
NN
tt t tt t
NN
tt tt tt
Sss sSss s
ss ss ss
(1)
For each discrete state component
{0,1, ... 1}
k
t
sm
probability of transition to a neighboring state is
higher than that to more distant states. Thus, we set
the transition probabilities on the basis of distances
between states as follows:
2
1
2
1
0
1()
(1 ) , {0, 1, ..., 1}
1
()
Pr( =u | )
0 {0,1,..., 1} {0,1,..., 1}
m
ii
tt
r
uv
uv m
m
rv
ssv
umorvm
(2)
This equation defines the transition probabilities
between all states in the state space.
5)
Observation function
The observation function
'| 'oas
p
indicates the
likelihood of the observation state being
'o
if the
system state
'
s
performs action
a
. Because the
selection actions do not affect the camera
observations or the computed scores, we set
APOMDP-basedCameraSelectionMethod
747

'| ' '| '
oas os
pp
. Also, we assume that the states in the
observation state space for different cameras are
independent. The observation probability is defined
as follows:
2
1
2
0
1()
(1 ) , {0,1,..., 1}
1
()
P
r( =u | )
0 {0,1,..., 1} {0,1,..., 1}
m
ii
tt
r
uv
uv m
m
rv
osv
umorvm
(3)
6)
Immediate rewards
For each action, we define an immediate reward
or cost to measure the degree of optimization that
would result from that action. We use the visual
score from each camera as a positive reward and use
the camera switching cost
cos t
c
, which represents the
visual jitter caused by frequent switching as a
negative reward. Therefore, the immediate reward
after camera selection is defined as
cos 1
(,) (1 ) ( )
ii i
tt t t t
R
Sa s c a
,
(4)
where
[0,1]
is the weight coefficient between the
positive and negative rewards, and the
function
1
()
i
t
a
= 1 if the camera selected at time step
t
was
also selected at time step
1
t
; else
1
()
i
t
a
= 0.
Given the belief state
()bs
for the camera system
state
s
at time step
t
, the scheduling agent attempts
to maximize the total reward
*
(())
Vbs
by selecting
the best camera
k
t
a
on the basis of the optimal
policy
*
. This condition is represented as follows:
* *
1
'
( ( )) max{ ( ( ), ) ( , , ') ( ( '))},
k
t
kk
tttt
aA
sS
V bs Rbs a psa sV bs
(5)
where
[0,1]
is a discount factor that controls the
future impact of rewards so that the effect of a
reward decays exponentially with respect to elapsed
time. If
o
is the observation after action
a
has been
executed, the next belief state
(')
o
a
bs
is calculated
on the basis of Bayesian theory as follows:
|'
|
(') ('|,)()
os a
o
a
sS
oab
p
bs pssabs
p
,
(6)
where
|oab
p
is a normalized constant defined as
||''|
'
()
oab os a s sa
sS sS
pppbs
.
Formula (5) can usually be computed iteratively
using dynamic programming; the computational
complexity increases exponentially with respect to
the scale of the problem. Therefore, a direct solution
to our POMDP is unfeasible because the problem is
intractable, and thus, we use the Perseus method
(Spaan and Vlassis, 2005), which is a point-based
approximation. We sample randomized a number of
belief state points
b
as a belief set and compute the
reward values for this belief set. We save the results
as a set of value vectors
12
{, ,...,}
n
in which
each vector
i
is associated with a selected action
i
a
so that the vector contains the same number of
components as the state space. When the central
controller selects the best camera online, it
transforms the observed states into belief states and
makes its decision on the basis of the following
relation:
arg max( ( ') )
i
i
aA
abs
,
(7)
The value vector
i
that has its inner product with
the current belief state at maximum is selected, and
the corresponding action
i
a
is selected as the best
camera.
3 VISUAL INFORMATION
MEASURE
In this section, we propose a measure that evaluates
the quality of the image captured by a camera by
extracting features indicating motion, properties of
objects, and special events and expressing features
as a motion score
i
m
S
, an object score
i
obs
S
, and an
event score
i
e
S
, respectively. The final visual score
as then calculated as follows:
12 3
ii i i
m obs e
SwSwS wS ,
(8)
where
1
w
,
2
w
, and
3
w
are weight coefficients such
that
3
1
1
i
i
w
. To simplify the exposition that follows,
we denote the motion scores, object scores, and
event scores without a superscript for the camera as
m
S
,
obs
S
, and
e
S
, respectively.
3.1 Global Motion
The degree of motion in a video stream reflects the
ability of the camera to capture real world changes.
We adopt the method presented in (Zhang et al.,
2011) for detecting moving objects and mitigating
the effects of illumination and shadows. Then we
determine the degree of global motion in a video
frame by calculating the ratio of the foreground area
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
748

to the area of the entire image. We assume that the
ratio will increase significantly when a new object
enters the scene or objects are close to the camera.
However, the ratio exceeding a certain threshold
implies that noise has been introduced by factors
such as illumination. Thus, we score the global
motion contained in a binary motion image as
follows:
1
1
,
1
m
rr
S
r
r
,
(9)
where
r
is the ratio of the area of the moving object
to the area of the entire image, and
is the best
ratio required by applications.
3.2 Object Properties
Individuals and special objects are the most
attractive elements in video surveillance
applications. To properly measure the properties of
objects in video streams, we focus on motion
saliency for individual objects and the degree to
which the objects in a scene occlude one another. To
detect the objects in a scene and appropriately
separate objects that are partially overlapped, we use
the method proposed by Hu (Hu et al., 2006) for
extracting bounding boxes for objects even when
they overlap. We then use the bounding boxes to
assign scores on the basis of local motion saliency
and occlusion between two overlapped objects.
Finally, we calculate an overall score for the
properties of the object in this scene as a weighted
sum of the two scores:
1
(1 ) ,
k
obs l oc
kOBS
SSS
OBS
,
(10)
where
k
l
S
is the local motion saliency score for
object
k
,
OBS
is the number of objects in the scene,
oc
S
is the occlusion score, and
is a weight factor.
1)
Local motion
We use the Harris 3D spacetime interest point
method (Laptev, 2005) to detect salient motion
details in the bounding boxes of objects and set the
saliency measure
k
l
S
of the
k
th object to be the
normalized number of 3D interest points detected in
the bounding box. Although the interest point
method is computationally expensive, we can
control the computation process by limiting the
search to a small region. Our experiments show that
this method can be effectively applied in real-time
video surveillance applications.
2)
Object occlusion
One of the most serious issues in video
surveillance, tracking, and other applications is
occlusion between objects in a scene. In multi-
camera systems, selecting a camera with the least
occlusion is an effective solution. For this purpose,
we measure the degree of occlusion between the
objects in a scene on the basis of intersection of the
bounding boxes for different targets and use this
measure to assign a score that reflects the occlusion.
The larger the areas with intersections, the lower the
score. Therefore, we define the occlusion score as
follows:
11
11
#( )
11
min(# ,# )
OBS OBS
oc
ij
iji
ij
OBS
S
Rc Rc
OBS
Rc Rc
,
(11)
where
i
Rc
denotes the bounding box of the
i
th
object and
#
denotes the area of the box.
3.3 Event Detection
It is necessary to detect events of interest in videos.
In this paper, we focus on the entrance of new
objects in a video Frame. We determine an entrance
region in the image called the “inner region” either
by predefining it or through training and monitoring
the ratio
1
r
of the area of motion in the inner region
to the entire area of the inner region. When
1
r
exceeding the threshold
1
Th
,
it indicates that an
object possibly enters the scene. To avoid false
detection with the ratio
1
r
due to the movement of
individuals present in the scene, we introduce an
external region around the entrance called the “outer
region” and determine the ratio
2
r
of the area of
motion in the outer region to the area of the entire
outer region. When
2
r
exceeds a threshold
2
Th
,
motion in the entrance is assumed to be the motion
of an object that is already in the scene. Also, an
entrance event is related to time. Therefore, we set
2
11 2 2
0,
T
e
e r Th and r Th
S
otherwise
,
(12)
where
T
is the time that has elapsed since the
condition for a new object entering the scene is
satisfied, so that the event score is gradually lowered
as time elapses.
APOMDP-basedCameraSelectionMethod
749

4 EXPERIMENTS AND RESULTS
4.1 Experimental Setup
We conducted experiments on a personal computer
to simulate the process of camera selection. We
generated optimal policies offline using the Perseus’
point-based method implemented using C++ and
quantified the camera scores on an eight-point scale
(
=8m
) and saved the optimal policies as value
vectors. We used publicly available datasets
composed of sequences from POM (Fleuret et al.,
2008) and HUMANEVA (Leonid et al., 2010) to
evaluate the performance of our method. The POM
dataset use four cameras, while the HUMANEVA
dataset uses seven cameras.
4.2 Visual Information Measurement
Analysis
In this section, we evaluate visual information scores
obtained from our method for the POM Terrace1
sequence. We denote the images from the four
cameras as C0, C1, C2, and C3. In the scene
captured by frames 1 through 700 of the Terrace1
sequence, no individual is present in the scene,
thereafter, one person enters the scene, followed by
two people with no occlusion, two people occluding
each other, and eventually three people are present
in the scene. After several experiments and analysis,
we set the parameters
,
,
12
,ww
, and
3
w
respectively. Therefore the global motion score
curve with
0.6
shown in Figure 1(a) reflects the
ability of the camera to capture the motion in the
observed scene, as well as the number of objects and
their distance from the camera. The numbers of
salient points for different views are shown in Figure
1(b). The object property scores with
0.6
in
Figure 1(c) indicate that cameras can detect the same
significant object properties, when global motion
plays a dominant role in the videos. Also, when
cameras provide similar global information, the local
motion saliencies are different owing to different
camera orientations and relative directions of motion
of the objects from these perspectives, for example,
the scores for frames 160 to 200 in Figure 1(c) and
the occlusion between objects is appropriately
detected. The curves in Figure 1(d) show the scores
for measuring entrance events that appropriately
indicate that two people have entered the scene
during this period. Finally, Figure 1(e) displays the
overall visual information score curves with the
weights
1
w
,
2
w
, and
3
w
set to 0.5, 0.2, and 0.3,
respectively. Thus, the evaluation of visual
information by our method in the analyzed video
streams can appropriately reflect changes in the
scene and details and special events of interest to
observers.
(a) Global motion scores
(b) Numbers of local salient points
(c) Object property scores,
0.6
(d) Entrance event scores for C2
(e) Visual information scores
Figure 1: Visual information measurement results.
4.3 Selection Results and Analysis
We compared our method of camera selection
(POMDP) to the state-of-the-art camera selection
methods based on greedy criteria for maximum
visual scores (Max), game theory 0 (LYM), and
Dynamic Bayesian Networks 0 (DBN). Our
experiments used the visual information scores
presented in Section 3 as the measures for Max and
POMDP, and the weight coefficient for the
immediate reward was
=0.8
. Figures 5(a) and 5(b)
show the camera selection results for the video
sequences POM Terrace1 and HUMANEVA Walk1;
the best camera was selected for each frame of the
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
750
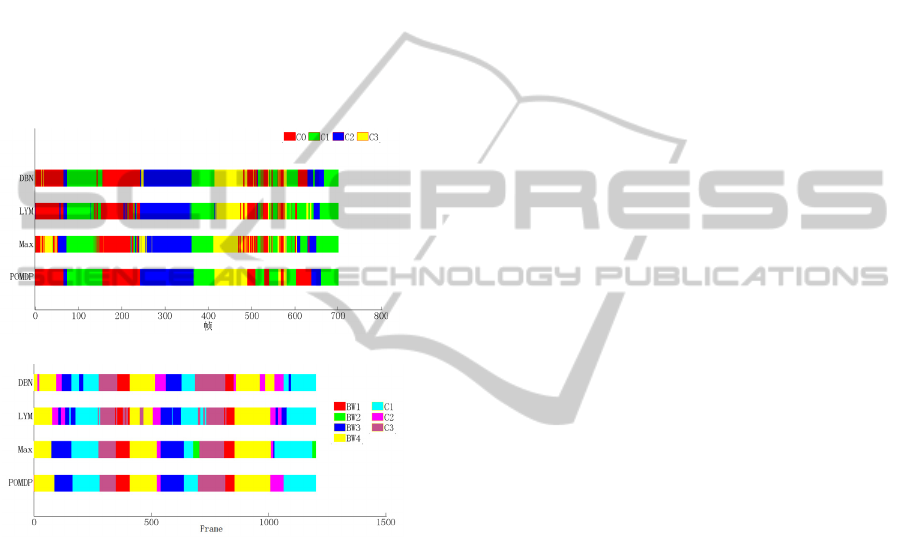
POM Terrace1 sequence on the basis of the camera
quality measures described in Section 4.2, and the
best camera was selected for the other sequences at
intervals of 5 frames. The camera selection results
indicate that there are some frequent camera
switches using LYM and DBN owing to false
selection because errors were introduced in the
motion detection process when there are two people
in the scene. Moreover, the LYM method was
especially prone to frequent switching when the
person utility is approximated to zero. In contrast,
our method effectively predicted future trends of the
visual information scores on the basis of history, and
this reduced the number of false selections, resulting
in smoother visual effects.
(a) POM Terrace1 selection results
(b) HUMANEVA Walk1 selection results
Figure 2: Selection results for the different methods.
5 CONCLUSIONS
Real-time selection of the most informative video
stream from a number of video streams has become
one of the key issues in visual analysis and
processing. The experimental results show that our
proposed POMDP-based method has a higher degree
of accuracy and is more stable than other methods.
In addition, we have proposed a visual information
score function for extracting and scoring visual
features associated with global motion, object
properties, and special events, and this function can
accurately reflect and describe the visual
information in a scene.
ACKNOWLEDGEMENTS
This work is supported by The National Natural Scie
nce Foundation of China (61272219, 61100110 and
61021062), The National High Technology Researc
h and Development Program of China (2007AA01Z
334), The Program for New Century Excellent Talen
ts in University of China (NCET-04-04605) and Th
e Science and technology program of Jiangsu Provin
ce (BE2010072, BE2011058 and BY2012190).
REFERENCES
Soro S, Heinzelman W. 2009. A survey of visual sensor
networks. Advances in Multimedia.
Li Y, Bhanu B. 2009. Utility-Based Camera Assignment
in a Video Network: A Game Theoretic Framework.
IEEE Sensors Journal 11(3).
Daniyal F., Taj M., Cavallaro 2010. A Content and task-
based view selection from multiple video streams.
Multimedia Tools and Applications ,46.
Bimbo A. D., Pernici F. 2006. Towards on-line saccade
planning for high-resolution image sensing. Pattern
Recognition Letters, 27(15).
Tessens L., Morbee M., Huang Lee, Philips W., Aghajan
H. 2008. Principal view determination for camera
selection in distributed smart camera networks. In
Second ACM/IEEE International Conference on
Distributed Smart Cameras.
Littman M. 2009. A tutorial on partially observable
markov decision processes. Journal of Mathematical
Psychology, 53(3).
Spaan M, Vlassis N. 2005. Perseus: Randomized point-
based value iteration for POMDPs. Journal of
Artificial Intelligence Research, vol 24.
Zhang S., Ding H., and Zhang W. 2011. Background
Modeling and Object Detection Based on Two-Model.
Journal of Computer Research and
Development,48(11).
Hu W. M., Hu M., Zhou X., et al. 2006. Principal axis-
base correspondence between multiple cameras for
people tracking. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 28(4).
Laptev I. 2005. On space-time interest points.
International Journal of Computer Vision. Vol 64.
Fleuret F., Berclaz J., Lengane R., Fua P. 2008. Multi-
camera people tracking with a probabilistic occupancy
map. IEEE Transaction on Pattern Analysis and
Machine Intelligence, vol 30(2).
Leonid S., Alexandru O., Michael J. 2010. HUMANEVA:
Synchronized Video and Motion Capture Dataset and
Baseline Algorithm for Evaluation of Articulated
Human Motion. Journal of Computer Vision.
APOMDP-basedCameraSelectionMethod
751
