Hierarchical Roadmap Approach to Rough Terrain Motion Planning

Michael Brunner, Bernd Br

uggemann and Dirk Schulz

Fraunhofer Institute for Communication, Information Processing and Ergonomics FKIE,

Wachtberg, Germany

Keywords:

Mobile Robot, Autonomy, Motion Planning, Rough Terrain, Active Actuators, Reconﬁgurable Chassis.

Abstract:

A reconﬁgurable chassis provides a mobile robot with a high degree of mobility and enables it to overcome

rough terrain in unstructured outdoor environments, like boulders or rubble, and challenging structures in

urban environments, like stairs or steps. Yet, many planning algorithms rarely exploit those enhanced capa-

bilities to the full extent, limiting these systems to mainly ﬂat environments also traversable by less capable

ﬁxed-chassis robots.

In this paper we introduce a two-stage roadmap approach to motion planning for reconﬁgurable robots which

utilizes the system’s actuators to traverse rough terrain and obstacles. First, by considering the platform’s op-

erating limits rather than the complete state, we quickly generate an initial path. Second, we reﬁne the initial

path in rough areas within a constrained search space. So we are able to plan appropriate actuator conﬁgu-

rations to traverse rough areas and ensure the system’s safety. Our algorithm does not categorize the terrain

and does not use any predeﬁned motion sequences. Hence, our planner can be applied to urban structures,

like stairs, as well as rough unstructured environments. We present simulation experiments to provide more

insight into our method and real-world experiments to prove the feasibility of our motion planning approach

on a real robot.

1 INTRODUCTION

Fixed-chassis robot platforms are commonly used to-

day. These platforms are limited to fairly ﬂat areas as

their design prevents them from traversing structures

with high edges or steep inclinations. The challenges

they can overcome are directly related to the diame-

ter of their wheels or their track heights and to some

extend to their centers of mass.

In addition to commonly used ﬁxed-chassis plat-

forms, there are systems with reconﬁgurable chassis.

Such a system is able to alter its state using actua-

tors to increase its traction, move its center of mass

to achieve a more stable state, or to lift itself over an

edge. This in turn enhances the mobility of the robot

and enables it to traverse a wide variety of environ-

ments which would be untraversable otherwise.

There exists a number of obstacles which are reg-

ularly encountered in robotic tasks. In urban en-

vironments single steps or stairs generally pose un-

traversable barriers for ﬁxed-chassis robots, but can

be overcome by systems with reconﬁgurable drives.

In unstructured outdoor environments the shape of

obstacles is almost endless including, for instance,

coarse debris, rubble, rocks, or simply steep inclina-

Figure 1: The Telemax robot is a tracked platform with four

actuators. It is able to traverse rougher terrain and to over-

come more obstacles than many ﬁxed-chassis robots.

tions in hilly environments. In most cases usual robots

have to circumvent the structures as traversal is im-

possible or too risky.

To drive a mobile robot across the above men-

tioned structures is a challenging task even for a

trained operator. There are many aspects which have

to be considered when driving over obstacles. Most

of them can be neglected when navigating on ﬂat ter-

rain. The stability of the robot is essential as the dan-

ger of falling over is greater on unstructured terrain.

Inertia and momentum will be increasingly important

if a robot is operated close to its limits. Moreover,

Brunner M., Brüggemann B. and Schulz D..

Hierarchical Roadmap Approach to Rough Terrain Motion Planning.

DOI: 10.5220/0004229000350046

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 35-46

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

varying contact points of the mobile system change

its behavior to actuator and driving commands.

We developed a hierarchical roadmap approach

to motion planning for reconﬁgurable robots. First,

we generate an approximate solution and reﬁne it

in a subsequent phase. The reﬁnement concentrates

on path segments in rough regions and accounts for

the actuators and the robot’s stability and traction.

Since the algorithm does not need a previous ter-

rain/structure classiﬁcation and does not use any pre-

deﬁned motion sequences, it can be applied to rough

outdoor environments as well as obstacles in urban

surroundings.

The remainder of this paper is organized as fol-

lows: section 2 names related work in this area of

research. Section 3 gives a short overview of our

method and names differences to related works. In

section 4 we introduce the roughness quantiﬁcation

used. Sections 5 and 6 describe the preliminary plan-

ning and the detailed motion planning phases, respec-

tively. In section 7 we discuss the parameters and

guidelines on how to set them. Experiments are pro-

vided in section 8, and we conclude in 9.

2 RELATED WORK

This section focuses on common approaches to rough

terrain path planning and on previous work using

methods similar to ours, i.e. hierarchical methods,

methods employing a graph-search and algorithms for

tracked robots.

Many algorithms for traversing rough terrain or

climbing structures, like stairs, involve a preceding

classiﬁcation step (e.g. using line detection to identify

stairs). This information is used to steer the system

during climbing, ﬁxing its heading to the gradient of

the staircase (Mourikis et al., 2007; ?). In (Dornhege

and Kleiner, 2007) a two dimensional A*-search on

behaviour maps is used to ﬁnd paths in rough environ-

ments for a tracked robot, similar to our model. The

path represents a sequence of predeﬁned skills en-

coded in the behavior maps. Fuzzy rules and Markov

random ﬁelds are used to classify the environment and

facilitate skill selection. A comprehensive approach

to traverse rough outdoor terrain as well as stairs is

presented in (Rusu et al., 2009). The framework in-

cludes a mapping component, a terrain classiﬁcation

and a two-phase planning algorithm. A high-level

planner samples a transition graph across different ter-

rain types and provides an initial path. In the second

phase specialized terrain sub-planners reﬁne the path

and return gait primitives for a RHex robot (e.g. stair-

climbing gait primitives). The approaches above are

limited to the set of terrain types or structures which

are imposed by their classiﬁcation scheme or the set

of motion sequences. On the contrary, our algorithm

does not rely on such a terrain/structure classiﬁcation

or on a set of motion sequences. Hence, it can be ap-

plied to a range of different environments.

We utilize a two-phase planning method which

produces an initial approximate solution followed

by a reﬁnement of the initial result. As in (Rusu

et al., 2009), other works also use a similar approach.

Kalakrishnan and colleagues introduced a controller

for fast quadruped locomotion over rough terrain

(Kalakrishnan et al., 2010). The controller decom-

poses the controlling task into several sub-tasks; ﬁrst,

they generate a terrain reward map using a learned

foothold ranking function and then produce an ap-

proximate path. In subsequent steps this ﬁrst so-

lution is improved to ensure kinematic reachability

and a smooth and collision-free trajectory. Like our

method, this is a multi-phase algorithm which re-

quires a map and implements a terrain analysis. How-

ever, our terrain analysis relies on a roughness quan-

tiﬁcation similar to (Molino et al., 2007) instead of

a ranking function of the actuator contacts. On the

contrary, the authors of (Kalakrishnan et al., 2010)

propose a reactive controller to traverse rough terrain

rather than a planning algorithm. Also the terrain in-

teraction of tracked robots is quite distinct compared

to the interaction of their legged robot.

Further, path reﬁnement can also be achieved by

path optimizing methods. CHOMP (Ratliff et al.,

2009) is an optimization method for continuous tra-

jectories using covariant gradient descent. It can op-

timize a path over a variety of criteria. Since it is ap-

plicable to unfeasible paths, it can be used as a stan-

dalone motion planner. STOMP (Kalakrishnan et al.,

2011) is a stochastic path optimizer using a path in-

tegral approach which does not require any gradient

information like CHOMP. Therefore, it can overcome

local minima and more general costs are applicable.

The major drawback of both methods is the limita-

tion to trajectories of a predeﬁned ﬁxed length. This

makes them inapplicable to our problem.

In this work we present a roadmap algorithm for

rough terrain path planning. Roadmap methods are

commonly applied to this problem in the literature.

An Anytime A*-search is used to ﬁnd paths in a multi-

resolution 4D state lattice for indoor environments

(Ruﬂi et al., 2009). The resolution of the lattice is

adjusted with respect to terrain or task characteristics

(e.g. narrow passages and goal proximity). The on-

line navigation utilizes a precomputation step which

determines paths for constrained areas. In (Miro et al.,

2010) the Fast Marching Method (FMM), a breadth-

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

ﬁrst search algorithm, is used on a 3D lattice to plan

stable paths for actively reconﬁgurable robots. The

system’s stability guides the search on a triangular

mesh of the environment. The actuators of the Pack-

bot robot used in this research are actively controlled

like the actuators of our Telemax platform.

The authors of (Hait et al., 2002) present an

approach to motion planning on rough terrain for

a wheeled robot with passive suspension using an

A*-search on a discretized conﬁguration space with

heuristics to limit the search space. The algorithm

considers the robot’s stability, mechanical limits, col-

lisions with the ground, and uncertainties on the ter-

rain model and the robot position. While they also

use a graph-search and measure the robot’s stability,

their algorithm does not have to account for actuators

due to the robot’s passive suspension. In contrast, we

must include the actively controlled actuators during

planning.

Magid et al. developed a rough terrain plan-

ning algorithm for a tracked robot with four actively

controlled crawlers (Magid et al., 2011). They use

a graph-search to ﬁnd motion sequences in a dis-

cretizied state space which also allows for motions

of controlled balance losing (e.g. insigniﬁcant falls

from small edges). However, rather than autonomous

navigation their application is to reduce the burden on

operators of search and rescue missions by propos-

ing paths through rough terrain. Unlike us, they

categorize the states to distinguish between different

transition types and consider controlled balance los-

ing states. However, they also plan on a discrete

state space and use a robot with actively controlled

crawlers, similar to our model.

3 OVERVIEW AND

DISCRIMINATORS

We start with a short overview of our algorithm. We

employ a hierarchical roadmap algorithm for motion

planning of actively reconﬁgurable robots in rough

environments. Although we developed our algorithm

for a tracked robot model, it is likely to be usable

for other articulated robot models with similar loco-

motion (e.g. wheeled platforms). Given a map we

compute the roughness of the environment (section

4). In the preliminary planning phase we build a mo-

tion graph according to the robot’s operating limits

and perform a graph-search to ﬁnd an initial path (sec-

tion 5). During the detailed motion planning step we

reﬁne the initial path in rough areas only. To this end,

we ﬁrst identify the path segments leading through

rough terrain. In ﬂat areas we do not perform a de-

Figure 2: Algorithm overview: First, a preprocessing step

analyzes the environment, followed by a preliminary plan-

ning step to ﬁnd an initial path and a detailed motion plan-

ning step which reﬁnes the preliminary solution in rough

areas using the actuators. In ﬂat areas, a default conﬁgura-

tion is applied.

tailed planning and apply default conﬁgurations in-

stead. We construct a state graph considering the ac-

tuators for a tube-like area around each rough path

segment. Using a graph-search we ﬁnd sequences of

robot states including the actuators (section 6). Con-

sult ﬁgure 2 for a scheme of our algorithm.

Our algorithm applies to tracked reconﬁgurable

robots like ours (see ﬁgure 1), but not to systems

with legged locomotion since the robot-terrain inter-

actions are very distinct. However, parts may be used

across different locomotion models, e.g. the rough-

ness quantiﬁcation and some of the metrics. Further,

looking at a complete robot system, we consider our

method to be the global planning component which

provides a plan followed by a feedback controller

which takes care of the plan execution using sensor

data for localization and obstacle avoidance in poten-

tially dynamic environments. Such a controller is be-

yond the scope of this paper.

In the following we state how our approach differs

from other approaches. First, we distinguish between

ﬂat and rough regions but do not rely on a previous

terrain classiﬁcation or on motion sequences a priori

designed to overcome speciﬁc challenges. Therefore,

we are not limited to a previously deﬁned set of terrain

classes or a set of motion sequences. However, our

contact points algorithm depends on a least-squares

plane approximation of the terrain (similar to (Magid

et al., 2008)), which works reasonably well on gen-

erally continuous surfaces, but not on discontinuous

environments. Nevertheless, our algorithm can be ap-

plied to traverse rough outdoor environments as well

as to overcome challenging structures in urban sur-

roundings.

Second, rather than taking the entire preliminary

path to guide the second detailed motion planning,

we solely consider path segments which lead through

rough areas. Since a detailed motion planning is not

necessary for path segments on ﬂat regions, planning

HierarchicalRoadmapApproachtoRoughTerrainMotionPlanning

can be signiﬁcantly simpliﬁed. Thus, we are able to

speed up planning.

Further, we use simpler robot and terrain mod-

els compared to planetary rover path planning ap-

proaches. They often utilize detailed dynamic and

mechanic models to capture the robot-terrain interac-

tion in depth (Howard and Kelly, 2007). Such models

are not always obtained easily and, thus, not necessar-

ily available for a speciﬁc robot model.

4 MAP AND TERRAIN

ROUGHNESS

Whether a given structure is traversable or not cannot

be determined easily. In 2D navigation this is usu-

ally addressed with a simple threshold on the height

differences; everything above this threshold is un-

traversable. For rough terrain and structures this ques-

tion becomes very hard to answer. While for 2D nav-

igation a 2D laser range ﬁnder is sufﬁcient to gather

the necessary information about the surroundings, a

3D sensor is often not enough to navigate through

rough environments due to the still limited sensor

coverage.

There are several reasons why it seems to be ex-

tremely difﬁcult to reliably decide on the traversabil-

ity of a structure and rough terrain based on local sen-

sor information solely. First, the dimensions of rough

terrain areas or challenging structures usually exceed

the sensor range; second, some sections of the envi-

ronment are often occluded; third, the limiting nar-

row view of sensors mounted on a mobile robot makes

it difﬁcult to get a sufﬁcient overview; ﬁnally, while

traversing rough terrain the robot’s state often orients

the sensors such that they are unable to cover the en-

vironment. For example, consider a ﬂight of stairs;

the very narrow view makes it hard to recognize the

stairs especially all the way to the top. While on the

stairs and close to the top the sensors cover very little

of the ground.

Additionally, the robotic system is exposed to un-

necessary risk if it starts to traverse an area which

turns out to be ultimately untraversable. A map allows

to decide whether an area is likely to be traversable

(without considering traction) and to assess the risk of

a path and whether driving through a hazardous area

is worth the risk or circumventing the region with rea-

sonable additional costs is more appropriate.

On the other side, the validity of the planning is

closely related to the level of detail of the map. Large

detailed maps are rarely available. This may be solved

by a coarse map with detailed patches for rough re-

gions. For our research, we use a map of the environ-

ment to avoid the complex perceptual task of 3D nav-

igation in rough terrain. This simpliﬁes the percep-

tual component and allows us to focus on the motion

planning aspect of this problem (Kalakrishnan et al.,

2010).

4.1 Risk Distribution

In our approach we use a heightmap to represent the

environment because it is simple to use and sufﬁcient

for our application. In order to assess the difﬁculty

of a position within the map, we use techniques from

image processing to compute a roughness quantiﬁca-

tion. First, we apply a maximum ﬁlter with a window

x,y

of size x × y to the height differences. A dis-

tortion of the range of values can be prevented by a

threshold h

max

which conveniently can be set to the

robot’s maximal traversable height. The threshold is

also used to scale the values to [0, 1]. Subsequently,

we apply a two dimensional Gaussian blur to smooth

the transitions. The maximum ﬁlter prevents isolated

peaks to be smoothed by the Gaussian ﬁlter. Figure 3

shows an example of the roughness quantiﬁcation.

Using an appropriate kernel size allows us to vir-

tually inﬂate hazardous areas. This is commonly done

in 2D navigation to keep the robot away from obsta-

cles. In contrast, our high risk areas are avoided by the

robot, but if required, will not prohibit traversal. An-

other beneﬁt is the simple and highly parallelizable

computation.

We use this roughness quantiﬁcation in both the

preliminary planning as well as the detailed motion

planning to adjust the planning according to the difﬁ-

culty of the environment.

5 PRELIMINARY PLANNING

Driving with actively reconﬁgurable robots on rough

terrain introduces a large planning space. Addition-

ally, aspects of the robot state, like the stability, are

not naturally satisﬁed and must be tested. The robot’s

actuators must be incorporated into the planning pro-

cess and the quality of the path must be judged not

only by its length, but also by the robot’s stability

and traction as well as the time required for transla-

tion, rotation and for actuator movements. First, we

employ a preliminary path search to quickly ﬁnd an

environment-driven path to the goal location. Subse-

quently, the path is used to constrain the search space

for the detailed planning. The detailed planning phase

determines the ﬁnal path consisting of the robot con-

ﬁgurations including the actuators.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

Figure 3: Two maps (left) and the corresponding roughness

quantiﬁcations (right); The risk value associated with a re-

gion is based on the height differences in this area. The

colors indicate the degree of roughness, ranging from green

for ﬂat regions over yellow to red, high risk areas.

Figure 4: The motion graph encodes the traversability of

the terrain. Areas with low height differences are white and

those with higher differences are red.

The preliminary planning utilizes the previously

discussed roughness quantiﬁcation to force the robot

to avoid hazardous areas and to prefer less risky

routes. In ﬂat regions the consideration of the com-

plete state is not necessary, whereas it is essential in

rough regions to increase the robot’s safety and en-

sure successful traversal. At the beginning we do not

know through which parts of the environment the path

will lead and if considering the complete state is re-

ally necessary. Therefore, we use the utmost operat-

ing limit of the mobile base setting the actuators aside.

The maximal traversable height of the robot consti-

tutes the operating limit. This way we obtain the least

restrictive limit. We build a motion graph which rep-

resents the ability of the mobile robot to traverse the

environment. The motion graph is based on the op-

erating limits of the robot. The transition costs are

given by the time t required to traverse a graph edge

e. Hereby, we reduce the permissible velocity accord-

ing to the terrain roughness:

t =

max



min

, (1 −w

· r) · v

max



where d is the length of edge e and r the maximal

Figure 5: The motion graph and the initial path split into

segments. Path segments through ﬂat regions are green;

segments through rough regions are purple.

risk of the vertices of e from the roughnes quantiﬁ-

cation. v

min

and v

max

are the minimal velocity the

robot should drive in high risk areas and the robot’s

maximal velocity, respectively. A safety weight w

allows the adjustment of the importance of safety.

Low safety weights diminish the inﬂuence of the risk,

hence lead to possibly shorter, but riskier paths. On

the contrary, high values increasingly force the robot

to take low risk paths. With those edge weights we

ﬁnd a path performing a usual graph-search, e.g. A*-

search or Dijkstra-search. Please refer to (Brunner

et al., 2012) for a more detailed description of the

metrics used by our algorithm.

While constructing the motion graph, we distin-

guish between areas of convenient risk levels (cor-

responding to moderate height differences) and re-

gions with higher risks (corresponding to challenging

height differences). See ﬁgure 4 for an example. We

use this distinction in the second planning phase to

split up the initial path into easy and hard segments

and to determine whether a detailed planning of the

robot motions is necessary.

6 DETAILED PLANNING

Rough terrain is more challenging and exposes the

mobile robot to a greater risk than ﬂat environments.

Therefore, we have to reﬁne the preliminary path in

rough areas using the complete robot states. The state

of a reconﬁgurable robot may look like

(x, y, z, θ, ψ, φ, v, ω, ˙v,

ω, a

, . . . , a

where the ﬁrst part describes the 6D pose of the robot.

The translational and rotational velocities are v and

ω, and the corresponding accelerations are depicted

by ˙v and

ω. a

are the control values of n actuators.

Reducing the state to the controllable part leads to

(x, y, θ, v, ω, ˙v,

ω, a

, . . . , a

HierarchicalRoadmapApproachtoRoughTerrainMotionPlanning

Figure 6: A tube around a rough segment (purple). The tube

is used to restrict the search space of the second planning

step.

The controllable parts still lead to a large in-

tractable search space. Therefore, we use the pre-

liminary path to constrain the robot’s state space for

the second planning phase. First, we split the path

into segments leading through ﬂat areas with low

risks and segments through rough regions with high

risk levels (see ﬁgure 5). For ﬂat segments the sta-

bility of the robot system can be safely assumed as

done in 2D navigation. Further, any robot conﬁgura-

tion may be applied with no or little risk. This way,

we avoid unnecessary planning in a high dimensional

space for easily accessible parts of the environment

and speed up planning. However, rough regions re-

quire an additional planning of the robot’s actuators to

ensure safety and task completion. We constrain the

state space further through focusing the reﬁnement on

tube-like areas around rough path segments (see ﬁg-

ure 6). This concentrates the search on the promising

region and makes the search feasible.

The detailed motion planning accounts for the en-

vironmental risk, the system’s stability and its trac-

tion, and for the time consumed by translation, rota-

tion and actuator movements. Since the robot’s speed

is very low when traversing hazardous areas, we put

forces and dynamic stability aside. To quantify the

stability and the traction we approximate the robot’s

footprint by the best ﬁtting plane (Magid et al., 2008).

This limits the current approach to mainly continuous

environments (e.g. hills, stairs, ramps, etc.).

The state graph models a discrete conﬁguration

space including the actuators. The edge weights are

deﬁned by a more accurate cost function which con-

siders more aspects of the robot state compared to the

preliminary planning. The cost c of an edge in the

graph breaks down into a safety part c

safety

and a time

part c

time

c = w · c

safety

+ (1 − w) · c

time

To quantify the safety, we examine the stability of

the robot S using a stability margin and the center of

mass, the traction T by considering the actuator an-

gles to the surface and the environmental risk r from

the roughness quantiﬁcation. We take the maximal

corresponding values of the involved vertices.

safety

r +

(S + T )

The time term includes the time required for transla-

tion t

and rotation t

as well as for actuator move-

ments t

. We use a triangle inequality to favor simul-

taneous execution.

time

+(1−w·c

safety

)

·t

+(1−w·c

safety

)·t

Moving the actuators needs time, but does not result

in spatial gain. Therefore, the time is a more appro-

priate measure than a distance measure. If the robot

is in an unsafe state (small values of c

safety

), we will

reduce the costs of actuator movements to enable the

robot to improve its state with small costs. A safety

weight w allows to adjust the robots behavior, result-

ing in faster paths with less actuator movements or

safer conﬁgurations through better suited actuator po-

sitions. However, adjusting the actuators to the cur-

rent situation requires more time, which increases the

execution time of the path. A detailed description of

the cost function and the different measures involved

can be found in (Brunner et al., 2012).

Using a graph-based model with the above men-

tioned costs allows us to perform a usual graph-

search, e.g. A*-search or Dijkstra-search, on the state

graph to ﬁnd the most stable and most efﬁcient path

to the goal. In contrast to the ﬁrst planning phase,

this path consists of complete robot states. If several

rough path segments exist, the path planning can be

parallelized.

The detailed motion planning can fail to ﬁnd a

valid path because the simpliﬁcation of the prelim-

inary planning discards several aspects of the robot

state, like the orientation and the actuators. In this

case, the preliminary planning must be triggered to

produce another path using a different safety weight

(see sections 7 and 8.1 for more information).

7 PARAMETER SETTINGS

The purpose of this section is to name the parameters

of our method and to give guidelines for appropriate

values. First of all, many of the quantities used in

our method are determined by the robot model or our

setup, e.g. the maximal traversable height or the max-

imal velocity.

The kernel size of the ﬁlters employed in the

preprocessing step to calculate the roughness values

should be the diagonal of the robot dimensions. So a

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

(a) A ramp. (b) A steep ﬂight of stairs.

Figure 7: The images show simulation environments posing different challenges and the robot during execution.

cell’s risk value considers the area of the robot’s foot-

print if it is placed at the same cell. As the robot di-

mensions change with the actuator conﬁgurations we

used the average of the smallest and largest conﬁgu-

ration, i.e. 100 cm for a squared window.

We consistently set the resolution of our maps to

5cm. The resolution of the motion graph should be set

such that the diagonal edges are shorter than the robot

length. Using half the robot size, we do not need any

validity tests between robot positions (i.e. vertices)

as the tests at the robot positions cover the transition

edges between them. To distinguish between ﬂat ar-

eas and rough areas we specify the maximal height

which can be traversed using a 2D navigation scheme

which does not use the actuators. We set the value

to 9 cm considering the robot’s capabilities using the

default actuator conﬁguration.

The size of the tube around rough segments deter-

mines the state space expansion for the detailed mo-

tion planning. We required all positions to be less

than 75 cm away from the path. Hence, we include

all positions (vertices) which need at most two edges

to reach the path provided a graph resolution of 30 cm

(half the Telemax length). We found including two

positions to either side of the path in the tube as a rea-

sonable trade-off between the state space expansion

and planning time.

The minimal velocity v

min

used in the cost terms

for the translation time speciﬁes the velocity the robot

should drive in the riskiest areas. We set the value to

0.12

, i.e. 10% of the robot’s maximal velocity of

1.2

The two safety weights w

for the preliminary

planning and w for the detailed motion planning allow

to adjust the importance of the safety for the planning

queries. The former will inﬂuence the major direction

of the path as it determines the initial path. The later

inﬂuences the robot conﬁgurations and the actuators.

Appropriate values depend on the application and the

robot model. However, we used values of w

= 0.75

and w = 0.5 in our experiments. Section 8.1 discusses

the effect of different values for w

and w.

(a) (b) (c)

Figure 8: Telemax actuator conﬁgurations: (a) completely

folded (all actuators at −90

◦

), (b) completely expanded (all

actuators at 80

◦

) and (c) maximal ground contact (all actu-

ators at 15

◦

8 EXPERIMENTAL RESULTS

We use a Telerob Telemax robot model in our re-

search, see ﬁgure 1. The robot is 60cm long, 40 cm

wide and weighs about 70 kg. It has four tracks which

can be rotated 170

◦

from entirely folded (−90

◦

) all

the way down (80

◦

) lifting the robot about 45 cm up

(see ﬁgure 8). Completely stretched the robot has a

length of 120 cm. The robot is equipped with a skid-

drive, and its maximal translational speed is 1.2

We present simulation experiments to illustrate

the effects of different safety weights on both plan-

ning phases. We also analyze the beneﬁt of the state

space restriction using the initial path. Further, we

describe two experiments with our Telemax robot in

real-world scenarios. They show that the plans of our

motion planner are feasible and can be executed by

our robot. We implemented a simple controller which

will adjust the actuators if they differ from the current

target angle, then rotates to the current target orienta-

tion, and ﬁnally drives. Its localization is solely based

on differential GPS.

8.1 Safety Weights

The safety weight of the preliminary planning phase

determines the major direction of the path as subse-

quent route corrections are limited to the tubes around

the rough segments. We performed several planning

queries with different safety weights keeping start and

goal location the same (ﬁgure 9). We increased the

safety weight w

from 0.0 to 1.0 with increments of

HierarchicalRoadmapApproachtoRoughTerrainMotionPlanning

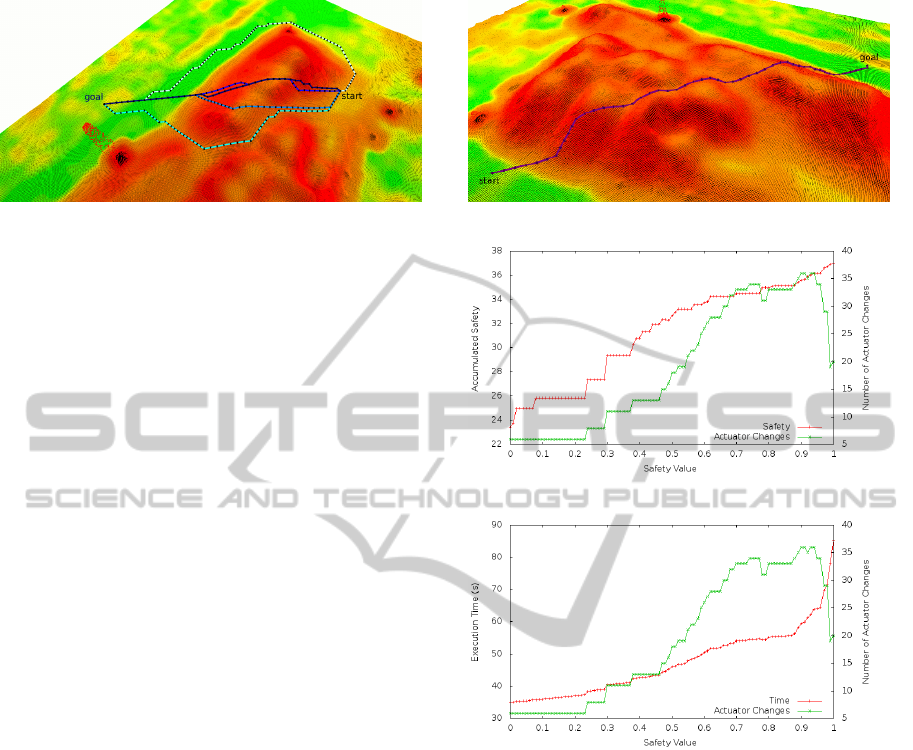
Figure 9: Inﬂuence of the safety weight on the preliminary

path planning. The image shows ﬁve paths with different

safety weights w

∈ {0.0, 0.25, 0.5, 0.75, 1.0}. The higher

the safety weight, the lighter is the coloring of the path. The

map is colored according to the risk values.

0.25. Disregarding safety completely (w

= 0.0) leads

to a straight path within the motion graph. Increasing

the value to 0.25 changes the path slightly, crossing

some of the high risk areas directly with the inclina-

tion. This reduces the time spend in those regions and

increases the safety by reducing the system’s roll an-

gle. At w

= 0.5 the path avoids the ﬁrst high risk

region and crosses the second straight. Further incre-

mentation (w

= 0.75) forces the path to follow the

dig in the middle of the hill and to circumvent the high

risk areas. Finally, with a value of w

= 1.0 the path

leads through the low risk regions around the hill.

Summarizing, as desirable for different missions,

the safety weight w

signiﬁcantly inﬂuences the direc-

tion of the path. A value around w

= 0.75 provides a

reasonable trade-off between safety and path length.

The safety weight of the second planning phase

mainly inﬂuences the choice of actuator conﬁgura-

tions; higher values will result in safer states at each

path position. To achieve a common basis for the

comparison, we selected an initial path, held it con-

stant for all second phase planning queries and shrunk

the tube to solely include the initial path (ﬁgure 10

top). Hence, we prevented impacts of different initial

paths and of route corrections within the tube during

the second planning phase. This also ﬁxes the number

of translations and rotations leaving only the actuator

conﬁgurations to be determined.

The middel image of ﬁgure 10 shows the accumu-

lated safety (inverted safety cost c

safety

) of the state

space paths plotted against the safety weight. Also on

the second y-axis we plotted the number of actuator

changes since they are the reason for the increasing

safety. Raising the safety weight leads to more actu-

ator adjustments in order to reach better suited robot

states in every position. Ultimately, this increases the

total safety of the ﬁnal path. Even though the actu-

ator changes decrease for higher safety weights, the

path safety still rises. This is explained by longer

sequences of stable conﬁgurations rendering changes

(a)

(b)

(c)

Figure 10: Inﬂuence of the safety weight on the detailed

motion planning: The path used for evaluation is shown on

top. We ﬁxed the initial path and reduced the tube to the

initial path, leaving only the actuator conﬁgurations muta-

ble. The curves show the total safety (inverted safety cost

safety

) and the execution time (seconds) of the ﬁnal state

space paths for different weights. As only the actuator con-

ﬁgurations are mutable, we include the number of conﬁgu-

ration changes on the second y-axis to illustrate their corre-

lation. The decrease in actuator changes for higher values

of w is due to long sequences of the same actuator conﬁgu-

ration. The increasing execution time for those values of w

are caused by higher rotation times in stable and high trac-

tion conﬁgurations.

unnecessary.

Similar, the bottom image of ﬁgure 10 displays

the execution time of the state space paths using dif-

ferent safety weights. The higher number of state

corrections through actuator adjustments results in a

higher execution time comprising the time required

for the adjustments. The execution time more than

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

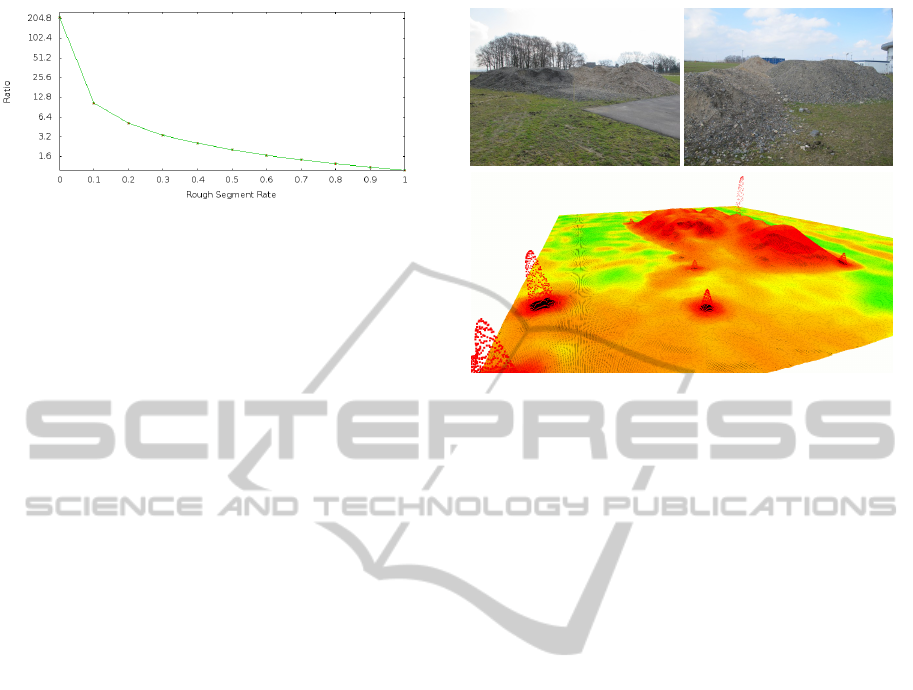
Figure 11: The effect the path segmentation into ﬂat and

rough segments has on the planning time. The y-axis is in

log-scale. The plot shows the mean ratios between the plan-

ning times without path segmentation and with path seg-

mentation for paths with different portions of roughness.

We performed 100 for each portion; 50 without path seg-

mentation and 50 with path segmentation.

doubles from about 35 s at w = 0.0 to roughly 85 s at

w = 1.0. The still growing execution time for falling

actuator changes towards higher values of w is caused

by lower rotational velocities of more stable conﬁg-

urations with higher traction. The rotational velocity

of reconﬁgurable robots depends on its actuator con-

ﬁguration. For example, consider the Telemax robot.

If the ﬂippers are completely stretched, the robot will

be 120 cm long with maximal ground contact. In this

conﬁguration rotation takes considerable longer than

with all ﬂippers folded.

Ultimately, the planning of the actuator positions

is essential to increase the safety of the robotic system

during rough terrain traversal. This leads to a signif-

icant increase of the path’s execution time due to the

time needed for the actuator adjustments and the in-

creased duration of rotational maneuvers.

8.2 Restriction of the State Space

This section discusses the restriction of the state space

of the detailed motion planning. We constrain the

state space using the preliminary path. As a detailed

assessment of the robot state is unnecessary in ﬂat ar-

eas, we consider only segments of the path which lead

through rough regions. This allows us to handle larger

planning queries as we focus on a subset of the state

space. Also, this signiﬁcantly reduces the planning

time.

The size of the state graph in the second plan-

ning phase depends on the chosen discretization, the

tube size and the length of the rough segments. If we

plan without a preliminary path constraining the state

space, the graph size depends on the size of the map

(if Dijkstra-search is used) or the roughness and the

distance to the goal (if a A*-search is used). Depend-

ing on these factors, our roadmap method will run out

of memory before returning a valid path.

Figure 12: The ﬁrst real-world scenario: Two pictures of

the hill of rubble and the the map of size 36.4 × 30.45 m

captured with a laser range ﬁnder.

Additionally to using just the initial path, we con-

centrate the path reﬁnement during the second plan-

ning phase on the path segments which pass through

rough areas. We generated several paths with differ-

ent portions of ﬂat and rough areas, ranging from 0%

to 100% in steps of 10%. We then performed 100

queries for each portion; 50 queries without splitting

the path into ﬂat and rough segments, i.e. consider-

ing the entire path to be rough, and 50 queries us-

ing the segments to plan only the rough portion in de-

tail. Figure 11 shows the mean values of the ratio be-

tween planning times without path segmentation and

with segmentation. The curve indicates that planning

the ﬂat path segments in detail increases the planning

time considerable. If more than one rough segment

exist, the second phase planning can be parallelized.

The planning queries of the real-world experiments

(see ﬁgures 13 and 16) have rough segment rates of

0.65 and 0.5, i.e. about 1.5 times faster and twice as

fast, respectively.

8.3 Real-world Experiments

We also performed tests with a real robot, the Telerob

Telemax model. The environments are shown in ﬁg-

ures 12 and 15. Both maps were recorded using a

laser range ﬁnder and were subsequently ﬁlled and

smoothed to facilitate planning. Their sizes are 36.4×

30.45m and 43.95 × 32.95 m, respectively. These are

quite large environments compared to related works

which usually focus on smaller patches of purely

rough terrain. For the tests we used the following

values: The resolution of the maps was 0.05m and

0.3m (half the robot length) for the motion graphs.

HierarchicalRoadmapApproachtoRoughTerrainMotionPlanning

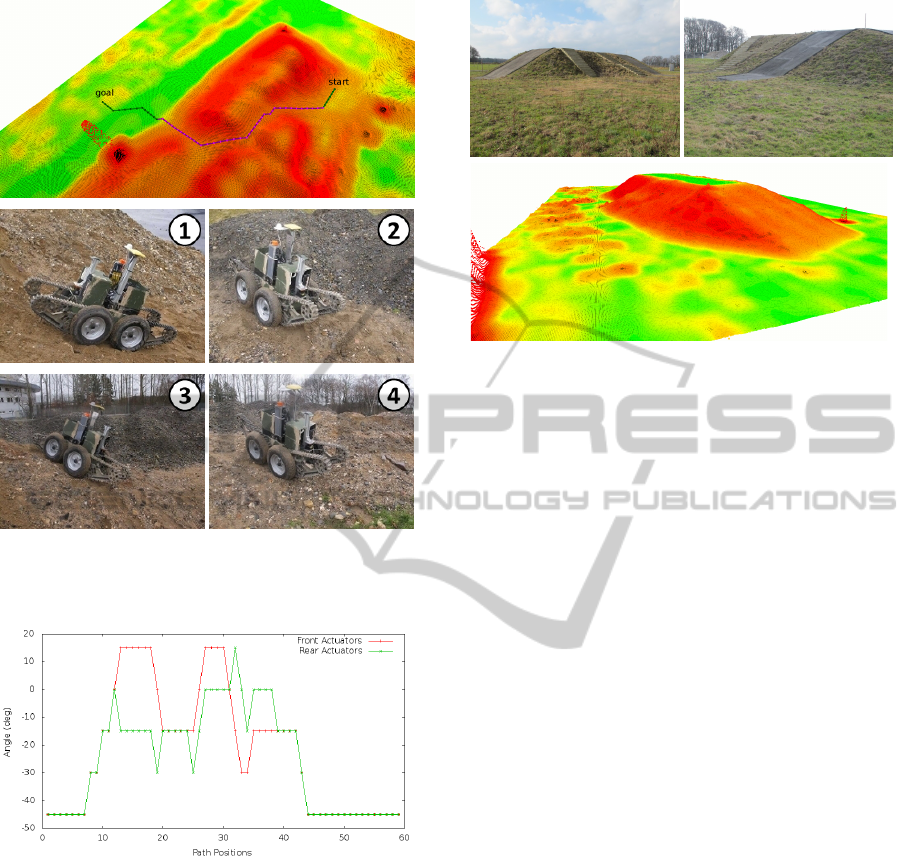
Figure 13: Results of the ﬁrst real-world experiment: The

top image shows the path followed by images of the robot

during the execution.

Figure 14: The actuator joint values of the path in the ﬁrst

real-world scenario on the hill of rubble. Values below zero

indicate folded conﬁgurations and values greater zero cor-

respond to expanded conﬁgurations.

We considered eight orientations in each position (45

◦

steps). The actuator values were bound to [−45

◦

, 45

◦

]

in steps of 15

◦

since more folded (smaller −45

◦

) or

more expanded (greater 45

◦

) conﬁgurations provide

little more beneﬁt. Further, both front, respectively

both rear actuators were required to be the same. The

safety weights were set to w

= 0.75 and w = 0.5. We

chose a folded conﬁguration with all actuator values

equal to −45

◦

as default conﬁguration. The default

conﬁguration was applied in ﬂat areas. The maxi-

mal ground contact is reached with all actuators at 15

◦

(see ﬁgure 8).

Figure 15: The second real-world scenario: Two pictures

of our testing hill and the the map of size 43.95 × 32.95 m

captured with a laser range ﬁnder.

We performed several planning queries of which

we present two, one for each map. Figures 13 and

16 show the planning queries and pictures of the ex-

ecution by our robot. In the ﬁrst scenario (ﬁgure 13)

the robot had to cross the hill of rubble through the

low risk areas, avoiding high elevations. The robot

was able to follow the proposed path while falling

over was prevented by the changing actuator conﬁgu-

rations (ﬁgure 14). The robot slipped casually due to

the small-grained material of the rubble.

Equally, the hill of the second scenario was tra-

versed by our robot given the plan shown in ﬁgure

16. The robot climbed the steep ramp with the most

stable conﬁguration, returned to the default setting on

the ﬂat top of the hill and adjusted the actuators anew

for the descent (see ﬁgure 17 for the actuator values).

The localization which was solely based on differen-

tial GPS, and the map’s noise caused some difﬁculties

for the controller when determining which part of the

plan should be executed.

However, in general, the robot was able to exe-

cute all plans of our motion planning algorithm and

successfully traversed the rough terrain. Further, the

proposed conﬁgurations proved to be suited to ensure

the safety of the robot. Problems during the execution

were related to terrain parameters (the small-grained

rubble) or to inaccuracy of the sensor data (the map

and the localization with differential GPS).

9 CONCLUSIONS AND FUTURE

WORK

In this paper we presented a motion planning algo-

rithm for robots with actively reconﬁgurable chassis

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

Figure 16: Results of the second real-world experiment:

The top image shows the planned path followed by images

of the robot during the execution.

Figure 17: The actuator joint values of the path in the sec-

ond real-world scenario on the testing hill. Values below

zero indicate folded conﬁgurations and values greater zero

correspond to expanded conﬁgurations.

to ﬁnd safe paths through rough terrain. We intro-

duced a hierarchical roadmap planner which quickly

determines a preliminary path considering the robot’s

operating limits rather than the complete states. The

initial path is used to constrain the high dimensional

state space of the second detailed motion planning

phase. We plan the robot’s motions in detail only in

rough areas where it is really necessary. Our algo-

rithm does not rely on predeﬁned motion sequences

or on a terrain classiﬁcation. Hence, it can be applied

to urban structures, like stairs, as well as to rough un-

structured environments.

Future work will focus on overcoming more chal-

lenging obstacles, like boxes or high steps. This will

require a more accurate modeling of the robots foot-

print and the contact points with the environment.

Also, we will investigate using optimal sampling-

based methods for continuous motion planning in the

second phase. The current controller is solely based

on differential GPS; we are planning to improve our

path execution through a better localization.

REFERENCES

Brunner, M., Brueggemann, B., and Schulz, D. (2012). Au-

tonomously Traversing Obstacles: Metrics for Path

Planning of Reconﬁgurable Robots on Rough Terrain.

In Int. Conf. on Informatics in Control, Automation

and Robotics. Best Paper Award.

Dornhege, C. and Kleiner, A. (2007). Behavior maps for

online planning of obstacle negotiation and climbing

on rough terrain. In IEEE/RSJ Int. Conf. Intell. Robots

Syst.

Hait, A., Simeon, T., and Taix, M. (2002). Algorithms

for Rough Terrain Trajectory Planning. Advanced

Robotics, 16:673–699.

Howard, T. M. and Kelly, A. (2007). Optimal Rough Terrain

Trajectory Generation for Wheeled Mobile Robots.

Int. J. Robot. Res., 26(2):141–166.

Kalakrishnan, M., Buchli, J., Pastor, P., Mistry, M., and

Schaal, S. (2010). Learning, Planning, and Control

for Quadruped Locomotion over Challenging Terrain.

Int. J. Robot. Res., 30:236–258.

Kalakrishnan, M., Chitta, S., Theodorou, E., Pastor, P., and

Schaal, S. (2011). STOMP: Stochastic Trajectory Op-

timization for Motion Planning. In Int. Conf. Robot.

Autom.

Magid, E., Ozawa, K., Tsubouchi, T., Koyanagi, E., and

Yoshida, T. (2008). Rescue Robot Navigation: Static

Stability Estimation in Random Step Environment.

LNCS - Simulation, Modeling, and Programming for

Autonomous Robots, 5325:305–316.

Magid, E., Tusubouchi, T., Koyanagi, E., Yoshida, T.,

and Tadokoro, S. (2011). Controlled Balance Los-

ing in Random Step Environment for Path Planning

of a Teleoperated Crawler-Type Vehicle. J. of Field

Robot., 28:932–949.

Miro, J., Dumonteil, G., Beck, C., and Dissanayake, G.

(2010). A kyno-dynamic metric to plan stable paths

over uneven terrain. In IEEE/RSJ Int. Conf. Intell.

Robots Syst.

Molino, V., Madhavan, R., Messina, E., Downs, A., Bal-

akirsky, S., and Jacoff, A. (2007). Traversability met-

rics for rough terrain applied to repeatable test meth-

ods. In IEEE/RSJ Int. Conf. Intell. Robots Syst.

Mourikis, A. I., Trawny, N., Roumeliotis, S. I., Helmick,

D. M., and Matthies, L. (2007). Autonomous Stair

Climbing for Tracked Vehicles. Int. J. Robot. Res,

26(7):737–758.

Ratliff, N., Zucker, M., Bagnell, J. A., and Srinivasa, S.

(2009). CHOMP: Gradient Optimization Techniques

HierarchicalRoadmapApproachtoRoughTerrainMotionPlanning

for Efﬁcient Motion Planning. In IEEE Int. Conf.

Robot. Autom.

Ruﬂi, M., Ferguson, D., and Siegwart, R. (2009). Smooth

Path Planning in Constrained Environments. In IEEE

Int. Conf. Robot. Autom.

Rusu, R. B., Sundaresan, A., Morisset, B., Hauser,

K., Agrawal, M., Latombe, J.-C., and Beetz, M.

(2009). Leaving Flatland: Efﬁcient Real-Time Three-

Dimensional Perception and Motion Planning. J. of

Field Robotics, 26:841–862.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence