Experimental Evaluation of the Effects of Manipulation by Merging in

Weighted Voting Games

Ramoni O. Lasisi and Vicki H. Allan

Department of Computer Science, Utah State University, Logan, U.S.A.

Keywords:

Agents, Weighted Voting Games, Power Indices, Manipulation, Merging.

Abstract:

Weighted voting games are subject to a method of manipulation, called merging. This manipulation involves

a coordinated action among some agents who come together to form a bloc by merging their weights in

order to have more power over the outcomes of games. We conduct careful experimental investigations to

evaluate the opportunities for beneﬁcial merging available for strategic agents using two prominent power

indices: Shapley-Shubik and Banzhaf indices. Previous work has shown that ﬁnding a beneﬁcial merge is NP-

hard for both the Shapley-Shubik and Banzhaf power indices, and leaves the impression that this is indeed

so in practice. However, results from our experiments suggest that ﬁnding a beneﬁcial merge is relatively

easy in practice. Furthermore, while it appears impossible to stop manipulation by merging for a given game,

controlling the quota ratio is desirable. Thus, we deduce that a high quota ratio reduces the percentage of

beneﬁcial merges. Finally, we conclude that the Banzhaf index may be more desirable to avoid manipulation

by merging, especially for high quota ratios.

1 INTRODUCTION

Weighted Voting Games (WVGs) are classic coop-

erative games which provide compact representation

for coalition formation models in human societies

and multiagent systems. Each agent in a WVG has

an associated weight. A subset of agents whose to-

tal weight is at least the value of a speciﬁed quota

is called a winning coalition. The weights of agents

in a game correspond to resources or skills avail-

able to agents, while the quota is the amount of re-

sources or skills required for a task to be accom-

plished. For example, in academia, professors put

their resources (i.e., weights) together to publish ar-

ticles (i.e., quota). The relative power of each agent

in WVGs reﬂects its signiﬁcance in the elicitation

of a winning coalition. To evaluate players’ power

in such games, prominent power indices such as

the Shapley-Shubik (Shapley and Shubik, 1954) and

Banzhaf (Banzhaf, 1965) indices are commonly used.

Recently, there is much interest in manipula-

tion (i.e., dishonest behaviors) by strategic players

in WVGs. These manipulations involve an agent or

agents misrepresenting their identities in anticipation

of gaining more power at the expense of other agents

in a game. See (Bachrach and Elkind, 2008; Aziz

and Paterson, 2009; Lasisi and Allan, 2010; Aziz

et al., 2011; Lasisi and Allan, 2011). In manipula-

tion by merging, which is also known as alliance or

collusion, two or more agents voluntarily merge their

voting weights to form a single bloc (Felsenthal and

Machover, 1998; Felsenthal and Machover, 2002). In

a beneﬁcial merge, merged agents are compensated

commensurate with their share of the power gained

by the bloc. The agents whose weights are merged

into a bloc are referred to as assimilated agents.

(Yokoo et al., 2005) consider collusion in open

anonymous environments, such as the internet. They

show that collusion in such environments can be dif-

ﬁcult to detect. Thus, the increased use of online sys-

tems such as trading systems and peer-to-peer net-

works, where WVGs are also applicable, means that

manipulation by merging remains an important chal-

lenge.

To provide insights into understanding the prob-

lem of manipulation by merging in WVGs, ﬁrst, we

recall that the problem of computing the Shapley-

Shubik and Banzhaf indices is NP-hard (Matsui and

Matsui, 2001). (Aziz et al., 2011) have also shown

that determining if there exists a beneﬁcial merge

for the manipulators is NP-hard using either of the

two indices to compute agents’ power. Although this

worst case complexity for manipulation by merging

is daunting, it is possible that real instances of WVGs

196

O. Lasisi R. and H. Allan V..

Experimental Evaluation of the Effects of Manipulation by Merging in Weighted Voting Games.

DOI: 10.5220/0004229401960203

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 196-203

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

are easy to manipulate. We note that real WVGs are

small enough that exponential amount of work may

not deter manipulators from participating in manipu-

lation by merging. Thus, according to (Keijzer et al.,

2010), the number of players in most real life exam-

ples of WVGs is between 10 and 50. Hence, manipu-

lations may, in some cases, be achieved in practice.

A careful investigation of effective heuristics for

manipulating such games by merging are yet to be

researched (Aziz and Paterson, 2009). This, we ar-

gue, may be primarily due to the inherent difﬁculty

of the problem. This is because the ability to ﬁnd

beneﬁcial merges depends on the characteristics of

the game. Some games have little opportunity for

merging while others could have many beneﬁcial

merges. So, in contrast to the work of (Aziz et al.,

2011), in this paper, we study experimental evalua-

tion of the effects of manipulation by merging using

various parameters of the games to analyze opportuni-

ties for beneﬁcial merging for the manipulators. This

will provide insight into understanding the problem to

both provide insights for heuristics and guide the deci-

sions of game designers. Our evaluation is carried out

using two prominent power indices: Shapley-Shubik

and Banzhaf indices, to compute agents’ power.

The NP-hardness results of ﬁnding a beneﬁcial

merge of the previous work for both the Shapley-

Shubik and Bazhaf indices leave the impression that

this is indeed so in practice. While ﬁnding the best

merging may be difﬁcult, results from our experi-

ments suggest that ﬁnding a beneﬁcial merge is rel-

atively easy in practice. While we may be powerless

to stop manipulation by merging for a given game,

we suggest controlling quota ratio, which is the per-

centage of weight needed to form a winning coali-

tion. The game designer may be able to control the

quota ratio. Thus, we deduce that when the quota ratio

of a game is high, the percentage of beneﬁcial merges

goes down. Finally, we conclude that the Banzhaf

power index may be more desirable than the Shapley-

Shubik power index to avoid manipulation by merg-

ing, especially for high values of the quota ratios.

2 RELATED WORK

(Felsenthal and Machover, 2002) characterize situ-

ations when it is advantageous or disadvantageous

for agents to merge into a bloc, and show that us-

ing the Shapley-Shubik index, merging can be ad-

vantageous or disadvantageous. (Aziz and Paterson,

2009) focus on the complexity of ﬁnding advanta-

geous merging. They show that for unanimity WVGs,

it is disadvantageous for a coalition to merge using

the Shapley-Shubik index to compute payoff. Also,

determining if there exists a beneﬁcial merge is NP-

hard for the Shapley-Shubik index. (Lasisi and Al-

lan, 2011) considers empirical evaluation of the extent

of susceptibility of three indices, namely, Shapley-

Shubik, Banzhaf, and Deegan-Packel indices to ma-

nipulation when agents engage in merging. Their re-

sults show that the Shapley-Shubik index is the most

susceptible to manipulation via merging among the

three indices. Furthermore, a recent work of (Lasisi

and Allan, 2012) proposes a search-based approach

to manipulation by merging. They show that manipu-

lators need to do only a polynomial amount of work

to ﬁnd improved beneﬁts when the size of the ma-

nipulators’ bloc is restricted to a constant 2 ≤ k < n,

where n is the number of agents in the WVG. The au-

thors then present a pseudopolynomial-time enumer-

ation algorithm that manipulators may use to ﬁnd a

much improved power gain over a random approach

using both the Shapley-Shubik and Banzhaf indices

to compute agents’ power.

It is important to note that none of these papers

deal with the experimental evaluation and analysis of

the type of beneﬁcial merging that we study here.

3 PRELIMINARIES

3.1 Weighted Voting Games

Let I = { 1, ··· , n} be a set of n agents and the

corresponding positive weights of the agents be

, ··· , w

}. Let a coalition S ⊆ I be a non-empty

subset of agents. A WVG G, with quota q involv-

ing agents I, is represented as G = [w

, . . . , w

;q]. We

assume that w

≥ w

≥ . . . ≥ w

. Note that this as-

sumption does not affect the deﬁnition of the game

or the generality of our results. Denote by w(S), the

weight of a coalition, S, derived as the summation of

the weights of agents in S, i.e., w(S) =

∑

j∈S

. A

coalition, S, wins in game G if w(S) ≥ q, otherwise

it loses. WVGs belong to the class of simple voting

games. In simple voting games, each coalition, S, has

an associated function v : S → {0, 1}. The value 1 im-

plies a win for S and 0 implies a loss. So, v(S) = 1 if

w(S) ≥ q, and 0 otherwise.

3.2 Power Vectors

(de Nijs and Wilmer, 2012) propose the use of power

vectors to evaluate heuristics for the well-known in-

verse problem (Fatima et al., 2008; Keijzer et al.,

2010) using the Banzhaf power index. We use power

vectors in this paper to illustrate the effects of small

ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames

197

changes in the weights of agents on their correspond-

ing powers in WVGs.

Deﬁne a power vector for a WVG G of n agents

as follows. Consider the weights of agents in G in a

non-increasing order. The power vector of G is an n-

dimensional vector v ∈ R

of the power of each of the

agents listed in order.

3.3 Shapley-Shubik Power Index

The Shapley-Shubik index quantiﬁes the marginal

contribution of an agent to the grand coalition (i.e.,

a coalition of all the agents). Each permutation of the

agents is considered. We term an agent pivotal in a

permutation if the agents preceding it do not form a

winning coalition, but by including this agent, a win-

ning coalition is formed. Shapley-Shubik index as-

signs power to each agent based on the proportion

of times it is pivotal in all permutations. We specify

the computation of the index using notation of (Aziz

et al., 2011). Denote by π, a permutation of the agents,

so π : {1, . . . , n} → { 1, . . . , n}, and by Π the set of all

possible permutations. Denote by S

(i) the predeces-

sors of agent i in π, i.e., S

(i) = { j : π( j) < π(i)}. The

Shapley-Shubik index, ϕ

(G), for each agent i in a

WVG G is

(G) =

∑

π∈Π

[v(S

(i) ∪ {i}) − v(S

(i))]. (1)

3.4 Banzhaf Power Index

An agent i ∈ S ⊆ I is referred to as being critical in

a winning coalition, S, if w(S) ≥ q and w(S\{ i}) <

q. The Banzhaf power index computation for an agent

i is the proportion of times i is critical compared to

the total number of times any agent in the game is

critical. The Banzhaf index, β

(G), for each agent i in

a WVG G is given by

(G) =

(G)

∑

j∈I

(G)

(2)

where η

(G) is the number of coalitions for which

agent i is critical in G.

4 PROBLEM DEFINITION

4.1 Problem Formalization

Let k and n be integers such that 2 ≤ k ≤ n. Let

I = {1, ··· , n} be a set of n agents and the correspond-

ing weights of the agents be {w

, ··· , w

}, where

∈ Z. Let G = [w

, . . . , w

;q] be a WVG of n agents

with quota q ∈ Z. Consider a manipulators’ coalition

C of k agents which is a k-subset of the n-set I. We as-

sume that C contains distinct k elements chosen from

I. Suppose the manipulators in C merge into a single

bloc denoted by &C, i.e., agents i ∈ C have been as-

similated into the bloc &C, then, we have a new set

of agents in the game after merging. Thus, the initial

game G of n agents has been altered by the manipu-

lators to give a new WVG G

′

of n− k + 1 agents con-

sisting of the bloc and other agents not in the bloc i.e.,

I\C. Note that the weights of the non manipulators

and the quotas in the two games remain the same.

Let φ be any of Shapley-Shubik or Banzhaf power

index. Denote by (φ

(G), . . . , φ

(G)) ∈ [0, 1]

the

power of agents in WVG G. Thus, for the manipu-

lating agents i ∈ C with power φ

(G) in game G, the

sum of the power of the k manipulators is

∑

i∈C

(G),

while that of the bloc formed by the manipulators in

game G

′

is φ

′

). The ratio τ =

′

)

∑

i∈C

(G)

gives a

factor of the power gained or lost by the manipulators

when they alter game G to give G

′

. The power index,

φ, is said to be susceptible to manipulation in WVG

G if there exists a G

′

such that τ > 1; the merging is

termed advantageous or beneﬁcial. If τ < 1, then the

merging is disadvantageous or non-beneﬁcial, while

the merging is neutral when τ = 1.

4.2 Examples of Merging in WVGs

We have used the Shapley-Shubik power index for

illustration in these examples. The manipulators and

their powers are shown in bold.

Example 1. Beneﬁcial Merging

Let G = [8, 8, 8, 6, 5, 5, 4,2,2, 2;28] be a WVG

of ten agents. The power vector of this game is

[0.167, 0.167, 0.167, 0.119, 0.099, 0.099, 0.067, 0.039,

0.039, 0.039]. Thus, the manipulators’ coalition

C = {3, 6, 7, 8, 9, 10}. The cumulative power of these

manipulators is 0.4481. Suppose the manipulators

merge their weights to form a bloc &C and alter G to

give G

′

= [23, 8, 8, 6, 5;28]. The power of the bloc is

′

) = ϕ

′

) = 0.8000 > 0.4481. The factor of

power gained by the manipulators is τ =

0.8000

0.4481

= 1.8.

Note that we have implicitly assumed that agents

in the blocs formed are working cooperatively and

have transferable utility. Thus, proceeds from merg-

ing can easily be distributed among the manipula-

tors. For instance, in this example, each manipula-

tors may ﬁrst be assign a payoff equal to what it

would get in the original game G, then, the gain (i.e.,

0.8000 − 0.4481 = 0.3519) derived from the altered

game G

′

can then be distributed among the members

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

198

of C using different solution concepts for revenue dis-

tribution from coalitional game theory.

Not all manipulation by merging are beneﬁ-

cial. Example 2 illustrates an example of a non-

beneﬁcial merge for the manipulators.

Example 2. Non-beneﬁcial Merging

Let G = [10, 9, 9, 9, 8, 7, 6, 6, 2,1;56] be a WVG

of ten agents. The power vector of this game

is [0.135, 0.121, 0.121, 0.121, 0.118, 0.118, 0.118,

0.118, 0.022, 0.008]. Thus, the manipulators’

coalition C = {4, 6, 8, 9, 10}. The cumulative

power of these manipulators is 0.3869. Sup-

pose these manipulators merge their weights

to form a single bloc &C and alter G to give

′

= [25, 10, 9, 9, 8, 6;56]. The power of the bloc is

′

) = ϕ

′

) = 0.3333 < 0.3869. The factor of

power lost by the manipulators is τ =

0.3333

0.3869

= 0.86.

5 MERGING PREDICTION

5.1 Using Power Vectors

Using power vectors, we provide further examples

to illustrate manipulation by merging. We have used

power vectors to illustrate the effects of small changes

in the weights of agents on their corresponding pow-

ers in WVGs. The Shapley-Shubik index is used in

this example. The small changes in the weight of

agents are related to weights changes when two or

more agents merge their weights to form a bloc,

thus providing some insights into merging. A cru-

cial observation is that we can have many games hav-

ing the same power vector. For example, the follow-

ing WVGs: [11, 9, 4;12], [11, 8, 5;12], [11, 7, 6;12],

[10, 9, 5;12], [10, 8, 6;12], and [10, 7, 7;12] all have

the same power vector [0.33, 0.33, 0.33], even though

the weights’ distribution of agents in the games differ.

In Figure 1, we consider all WVGs of 3 agents

such that the total weights of the agents in each

game is 24. Figures 1(a), 1(b), and 1(c) are for the

cases when the quotas q of the games are 12, 16,

and 18, respectively. The y-axis indicates the possi-

ble weights of the ﬁrst agent while the x-axis indi-

cates the possible weights of the second agents in the

games. Note that since agents weights are given in

non-increasing order, the possible weights for the sec-

ond agent are dependent on the weights of the ﬁrst

agent. The possible weights of the third agents are

not shown since they can implicitly be derived hav-

ing known the weights of the ﬁrst two agents.

Similar to only the 4 power vectors that are attain-

able in WVGs of 3 players using the Banzhaf index

(de Nijs and Wilmer, 2012), there are also 4 different

power vectors for these games when the number of

agents is 3 and using the Shapley-Shubikindex. These

power vectors are coded as 1, 2, 3, and 4 below:

1 : [0.33, 0.33, 0.33]

2 : [0.50, 0.50, 0.00]

3 : [0.67, 0.17, 0.17]

4 : [1.00, 0.00, 0.00]

with the games of each power vector representing ap-

propriate regions shaded in Figure 1. It is easy to

observe the following facts which have impacts on

weight changes as it relates to merging:

• The number of different power vectors is a func-

tion of the number of agents, n, in the games.

• The size of the region (associated with a particular

power vector) changes with the quota.

• Some weight vectors are volatile to changes

with respect to small changes in weight (such

as [11, 7, 6;18]) while others are not (such as

[12, 11, 1;18]).

5.2 Difﬁculty of Merge Prediction

A visual description clariﬁes manipulation by merg-

ing in WVGs. We use the Shapley-Shubik power in-

dex for illustration. Consider a WVG of three agents

denoted by the following patterns: Agent 1 ( ),

Agent 2 ( ), and Agent 3 ( ). The weight of each

agent in the game is indicated by the associated length

of the pattern. A box in the pattern corresponds to a

unit weight. Each row represents a permutation. Sup-

pose all permutations of the three agents are given as

shown in Figure 2. We can use the same ﬁgure to con-

sider a range of quotas from 1 to 6 for the game. The

Shapley-Shubik indices of the three agents are com-

puted from the ﬁgure and shown in the associated ta-

ble of the ﬁgure. These power indices for the agents

in the game correspond to using various values of the

quota for the same weights of the agents.

Consider a manipulation where Agent 1 and

Agent 3 merge their weights to form a new agent,

say, Agent X. In this case, Agent 1 and Agent 3

cease to exist since they have been assimilated by

Agent X. Thus, we have only two agents (Agent X

and Agent 2) in the altered WVG. Figure 3 shows the

results of the merging between Agent 1 and Agent

3. Notice that the number of rows has been reduced

to two, as there are now only two possible order-

ings. Consider the cases when the quota of the game is

1 or 6, the power of the assimilated agents for Agent

X from Figure 2 shows that Agent 1 and Agent 3 each

has a power of

for a total power of

. The power of

ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames

199

Figure 1: Using power vectors to illustrate the effects of small changes in the weights of agents on their corresponding

Shapley-Shubik powers in WVGs.

Figure 2: Six permutations of 3 agents and the power in-

dices of the agents for values of quota from q = 1 to q = 6.

Agent X which assimilates these two agents in the two

cases is each

. Also, the power of the manipu-

lators stays the same for the cases where the quota is

either 2 or 5. Speciﬁcally, the sum of the powers of

Figure 3: Manipulation by merging between Agent 1 and

Agent 3 (from Figure 2) to form a new Agent X. The indices

of Agent X and Agent 2 computed by Shapley-Shubik index

after merging for various values of quota are also shown.

Agent 1 and Agent 3 is

for these cases. This is also

true of Agent X for these cases. Finally, for the cases

where the quota of the game is 3 or 4, the power of

Agent X is 1 which is greater than

, the sum of the

powers of Agent 1 and Agent 3 in the original game.

Note the difﬁculty of predicting what will happen

when manipulators engage in merging. This illustra-

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

200

tion also shows that the choice of the quota of a game

is crucial in determining the distribution of power of

agents in a WVG. An apparent question that concerns

the manipulators from the illustration above is the fol-

lowing : Can effective merging heuristics be found

even though predicting beneﬁcial merging is difﬁcult?

6 EXPERIMENTS

6.1 Simulation Environments

We perform experiments to provide understanding

and analysis of the opportunities for beneﬁcial merg-

ing by manipulators in WVGs. We randomly gener-

ate WVGs. The weights of agents in each game are

chosen such that all weights are integers and drawn

from a Normal distribution, N(µ, σ

), where µ and σ

are the mean and variance. We have used µ = 50 and

several values of standard deviation σ from the set

{5, 10, . . . , 40}. The number of agents, n, in each of

the original WVGs is 10. For clarity of presentation,

we have restricted the number of assimilated agents,

k, in each game to 2. This is consistent with the as-

sumptions of previous work on merging (Aziz et al.,

2011; Lasisi and Allan, 2012) and coalition formation

(Shehory and Kraus, 1998), as manipulators’ blocs of

small sizes are easier to form, and more importantly

to the manipulators, they are less likely to be detected

by other agents in the games. Apart from this, we also

believethat an indepth understanding of this case (i.e.,

k = 2), will provide necessary background in under-

standing of the general case of when k > 2.

We have used a total of 200 distinct WVGs for

our experiments. For each game, we vary the quota

of the game from

w(I) + 1 to w(I) in steps of 10,

where w(I) is the sum of the weights of all agents in

the game. We then compute the factor of increment

for each assimilated bloc of size 2 in a game using

the two power indices. The evaluation is carried out

for the proportion of beneﬁcial merges in a game and

the quota ratio,

w(I)

quota

total weight

. The quota ratios for

the experiments range from 0.5 to 1.0, and indicate

the fraction of the total weight needed for the quo-

tas. A quota ratio of 1.0 suggests the existence of a

type of WVGs referred to as unanimity WVGs, where

all agents in a game are needed to form a winning

coalition. Thus, a winning coalition always exists in

the games. In other words, the quota ratio is a measure

of the percentage of weight needed to form a winning

coalition.

We consider all possible manipulators’ blocs of

size 2. The percentage of beneﬁcial merge for a quota

ratio is the fraction of cases whose factors of incre-

ment is greater than a speciﬁed value of τ. We tweak

τ using different values to see how the percentage

of beneﬁcial merges varies and provide discussions

of the effects noticed in the next subsection. The

pseudocode to compute the percentage of beneﬁcial

merges for each quota ratio is given in Figure 4.

percentBeneficialMerge(Agents I, WVG G,

) {

for quota q of G from

w(I)+1 to w(I) step 10

successCount = 0;

totalCount = 0;

for each manipulators’ bloc b of size 2

compute factor of increment f for b

if f

> τ

then

successCount++;

totalCount++;

end for

quotaRatio = q / w(I);

percentBenefit = successCount / totalCount;

end for

}

Figure 4: Pseudocode to compute the percentage of beneﬁ-

cial merges for each quota ratio.

6.2 Discussion of Simulation Results

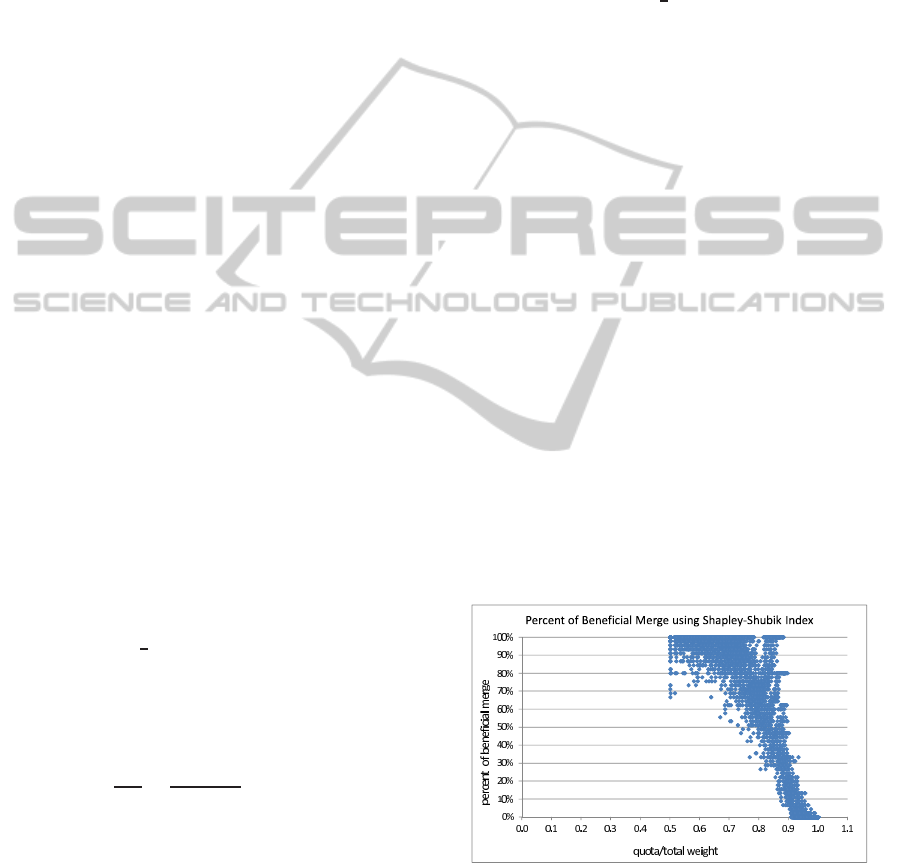
We present the results of our experiments. Figures 5

and 6 are indications of the opportunities for bene-

ﬁcial merging available for the manipulators. The x-

axis is the quota ratio and the y-axis is the percentage

of beneﬁcial merging available to the manipulators

when a beneﬁcial merge is deﬁned strictly as τ = 1,

i.e., a factor of power gain greater than 1.

Figure 5: Percentage of beneﬁcial merging for various val-

ues of quota ratio when a beneﬁcial merge is deﬁned to have

a factor of power gain greater than 1.0 (Shapley-Shubik).

The theoretical results of (Aziz et al., 2011) on

merging show that ﬁnding a beneﬁcial merge is NP-

hard for both the Shapley-Shubik and Bazhaf indices,

and leave us with the impression that this is indeed so

ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames

201

Figure 6: Percentage of beneﬁcial merging for various val-

ues of quota ratio when a beneﬁcial merge is deﬁned to have

a factor of power gain greater than 1.0 (Banzhaf index).

in practice. Figures 5 and 6 show that ﬁnding a beneﬁ-

cial merge is relatively easy in practice, at least for the

WVGs we considered, and restricting each manipula-

tors’ blocs to size 2. In reality, ﬁnding the best merg-

ing may not even be desirable, as it assumes every

agent will be willing to merge. Manipulators cannot

petition every agent to see if they are willing to merge,

as the manipulators would have announced their in-

tent to cheat. However, a dishonest agent may ﬁrst

discover opportunities for beneﬁcial merging before

suggesting such merge to other would-be manipula-

tors.

While it appears from the ﬁgures that we may

be powerless to stop merging for a given game, the

game designer may be able to control the quota. Thus,

a high quota ratio reduces the opportunities for dis-

honesty as the percentage of beneﬁcial merges goes

down. Using the two indices to compute agents’

power, we can deduce from Figures 5 and 6 that the

Banzhaf index is more desirable to avoid cheating es-

pecially for high ratios. This is because the percent-

ages of beneﬁcial mergings for high values of the

quota ratio using the Banzhaf index are smaller com-

pare to those of the Shapley-Shubik index. Table 1

shows the means and standard deviations of the fac-

tor of power gained by manipulators from Figures 5

and 6. This shows that, on average, manipulation by

merging is easier using the Shapley-Shubikindex than

using the Banzhaf index. This also indicates that the

Banzhaf index may be more desirable to avoid manip-

ulation in this situation.

For the second set of experiments, we consider

a more realistic scenario for the manipulators. Even

though we have deﬁned a beneﬁcial merge as a merge

in which manipulators have a power gain with τ >

1, manipulators may only be interested in beneﬁcial

merge with appreciable gains as the risks of being de-

tected by the mechanism may exceed the anticipated

beneﬁts. We have restricted the minimal beneﬁcial

Table 1: The means and standard deviations of the factor of

power gained for Figures 5 and 6 using the two indices.

Indices Shapley-Shubik Banzhaf

Mean 1.142 1.062

Standard deviation 0.182 0.057

rate to τ = 1.05 or 1.10, and do not notice appreciable

change in the percentage of beneﬁcial merging com-

pared with those of Figures 5 and 6. Thus, we do not

report them here.

However, for value of τ = 1.15, which represents

at least a 15% anticipated increment from the original

power of the manipulators, we noticed a sharp con-

trast from earlier results. This is an interesting and a

positive result for the designer of a game as it shows

that the percentageof beneﬁcial merges drops for both

power indices. See Figures 7 and 8.

Figure 7: Percentage of beneﬁcial merging for various val-

ues of quota ratio when a beneﬁcial merge is deﬁned to have

a factor of power gain greater than 1.15 (Shapley-Shubik).

Figure 8: Percentage of beneﬁcial merging for various val-

ues of quota ratio when a beneﬁcial merge is deﬁned to have

a factor of power gain greater than 1.15 (Banzhaf index).

Consider Figure 7. The opportunities for beneﬁ-

cial merge for the manipulators using the Shapley-

Shubik index may still be high, even when the factor

of power gained has been increased to τ = 1.15. How-

ever, for the case of the Banzhaf index (see Figure 8),

the maximum percentage of beneﬁcial merge avail-

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

202

able for the manipulators is considerably less. We ar-

gue that it is not unlikely that low percentage of bene-

ﬁcial merge may discourage manipulators in engaging

in manipulation by merging if these conditions that

we describe prevail and also using the Banzhaf power

index to compute agents’ power.

7 CONCLUSIONS

This paper considers experimental evaluation of the

effects of manipulation by merging in weighted vot-

ing games. We conduct careful experimental investi-

gations and analyses of the opportunities for beneﬁ-

cial merging available for strategic agents to engage

in such manipulation using two well-known power

indices, the Shapley-Shubik and Banzhaf power in-

dices to compute agents’ power. The following gives

account of our main contributions.

First, we examine effects of small changes in the

weights of agents on their corresponding powers in

weighted voting games. This is illustrated by show-

ing that power vectors are often unchanged. Second,

we argue and provide empirical evidence to show

that despite ﬁnding the optimal beneﬁcial merge is

an NP-hard problem for both the Shapley-Shubik and

Banzhaf power indices, ﬁnding beneﬁcial merge is

relatively easy in practice. Hence, there may be little

deterrent to manipulation by merging in practice us-

ing the NP-hardness results. Third, while it appears

that we may be powerless to stop manipulation by

merging for a given game, we suggest a measure,

termed quota ratio, that the game designer may be

able to control. Thus, we deduce that a high quota

ratio decreases the number of beneﬁcial merges. Fi-

nally, using the two power indices to compute agents’

power, we conclude that the Banzhaf index may be

more desirable to avoid manipulation by merging, es-

pecially for high values of quota ratios.

There are several areas of ongoing research on

this problem. First, we seek to expand our experimen-

tal evaluations to consider and understand the gen-

eral case of manipulators’ blocs of size greater than

2. Second, we seek to understand the effects of other

parameters of our experiments on the opportunities

for beneﬁcial merging for the manipulators. Finally,

we also seek to provide careful investigations of ef-

fective heuristics for manipulation by merging.

ACKNOWLEDGEMENTS

This work is supported by NSF research grant

#0812039 entitled “Coalition Formation with Agent

Leadership”.

REFERENCES

Aziz, H., Bachrach, Y., Elkind, E., and Paterson, M. (2011).

False-name manipulations in weighted voting games.

Journal of Artiﬁcial Intelligence Research, 40:57–93.

Aziz, H. and Paterson, M. (2009). False-name manipula-

tions in weighted votinggames: splitting, merging and

annexation. In 8th Intl. Conf. of AAMAS, pages 409–

416, Budapest, Hungary.

Bachrach, Y. and Elkind, E. (2008). Divide and con-

quer: false-name manipulations in weighted voting

games. In 7th Intl. Conf. of AAMAS, pages 975–982,

Estoril, Portugal.

Banzhaf, J. (1965). Weighted voting doesn’t work: a math-

ematical analysis. Rutgers Law Review, 19:317–343.

de Nijs, F. and Wilmer, D. (2012). Evaluation and improve-

ment of Laruelle-Widgr´en inverse Banzhaf approxi-

mation. CoRR, abs/1206.1145.

Fatima, S., Wooldridge, M., and Jennings, N. R. (2008). An

anytime approximation method for the inverse Shap-

ley value problem. In 7th Intl. Conf. of AAMAS, pages

935–942, Portugal.

Felsenthal, D. S. and Machover, M. (1998). The Measure-

ment of Voting Power: Theory and Practice, Problems

and Paradoxes. Edward Elgar, Cheltenham.

Felsenthal, D. S. and Machover, M. (2002). Annexation

and alliances: when are blocs advantageous a priori.

Social Choice and Welfare, 19(2):295–312.

Keijzer, B., Klos, T., and Zhang, Y. (2010). Enumeration

and exact design of weighted voting games. In 9th Intl.

Conf. of AAMAS, pages 391–398, Toronto, Canada.

Lasisi, R. O. and Allan, V. H. (2010). False name manip-

ulations in weighted voting games: Susceptibility of

power indices. In 13th Workshop on Trust in Agent So-

cieties of AAMAS, pages 139–150, Toronto, Canada.

Lasisi, R. O. and Allan, V. H. (2011). Annexations and

merging in weighted voting games - the extent of sus-

ceptibility of power indices. In 3rd Intl. Conf. of

ICAART, pages 124–133, Rome, Italy.

Lasisi, R. O. and Allan, V. H. (2012). A search-based ap-

proach to annexation and merging in weighted voting

games. In 4th Intl. Conf. of ICAART, pages 44–53,

Vilamoura, Algarve, Portugal.

Matsui, Y. and Matsui, T. (2001). NP-completeness for cal-

culating power indices of weighted majority games.

Theoretical Computer Science, 263((1-2)):305–310.

Shapley, L. S. and Shubik, M. (1954). A method for evalu-

ating the distribution of power in a committee system.

American Political Science Review, 48:787–792.

Shehory, O. and Kraus, S. (1998). Methods for task allo-

cation via agent coalition formation. Artiﬁcial Intelli-

gence, 101(1-2):165–200.

Yokoo, M., Conitzer, V., Sandholm, T., Ohta, N., and

Iwasaki, A. (2005). Coalitional games in open anony-

mous environments. In American Association for Ar-

tiﬁcial Intelligence, pages 509–514.

ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames

203