Reconstructing Archeological Vessels from Fragments using Anchor

Points Residing on Shard Fragment Borders

Zexi Liu

, Fernand Cohen

and Ezgi Taslidere

Department of Electrical and Computer Engineering, Drexel University, Philadelphia, U.S.A.

Keywords: Intrinsic Geometric Features, Curvature, Inflection, Mending, Archeological Shards, Global Constraint.

Abstract: This paper presents a method to assist in the tedious process of reconstructing ceramic vessels from

excavated fragments. The method models the fragment borders as 3D curves and uses intrinsic differential

anchor points on the curves. Corresponding anchors on different fragments are identified using absolute

invariants and a longest string search technique. A rigid transformation is computed from the corresponding

anchors, allowing the fragments to be virtually mended. A global constraint induced by the surface of

revolution (basis shape) to decide on how all pairs of mended fragments are coming together as one global

mended vessel is used. The accuracy of mending is measured using a distance error map metric. The method

is tested on a set of 3D scanned fragments (313 pieces) coming from 19 broken vessels. 80% of the pieces

were properly mended and resulted into alignment error at the scanner-resolution-level. The method took 59

seconds for mending pieces plus 60 minutes for 3D scans as compared to 12 hours for stitching manually.

1 INTRODUCTION

The mending of unearthed archeological ceramic

shards to reconstruct vessels that the fragments once

formed is currently a tedious and time-consuming

process. Nevertheless, it is a vital step in interpreting

the archeological record and an important

component in understanding and preserving cultural

heritage.

There are a variety of existing techniques for

characterizing and reconstructing fragments. They

can be classified into four categories, which are

point-to-point, curve, surface, and shape descriptor

matching. The unifying idea rests on finding

corresponding parts, matching, aligning, and gluing

all matching parts together.

Ucoluk and Toroslu (Ucoluk and Toroslu, 1999)

proposed a 3D curve matching approach for the

mending of thin-shell fragments, based on string

matching of the curvature and torsion values on the

discrete 3D curve points. The string matching

algorithm is further elaborated in (Rodriguez, Last et

al., 2004).

For thick-shell fragments, i.e. broken pieces with

large contact surfaces, Papaioannou et al.

(Papaioannou and Karabassi, 2003) presented a

method based on polygonal surfaces. They introduce

a matching error between complementary surfaces

that exploits the z-buffer algorithm. This method is

then extended to incorporate curve matching ideas.

In this paper, we select a feature-based approach

that identifies corresponding anchor points on

different shards to help in the mending process. The

main advantages of our method are: (i) the

extraction of novel anchor points residing on the

fragments’ borders. These are differential intrinsic

points sometimes not easily seen by the naked eyes,

hence the method looks at features that can go

beyond human visual mending; (ii) introducing a

simple and easy method for the extraction of the

fragment border through the use of a Delaunay

triangulation on the 3D data, followed by the

detection of those triangles edges that are not shared

by two abutting triangles. It results into a set of self-

induced ordering of points of the border edges by

simply following the end points of the abutting

border edges in a clockwise or an anticlockwise

direction. These ordered endpoints are the fragment

border curve points; (iii) establishing

correspondences between anchor points on

fragments through the use of absolute invariants and

a novel string matching method; (iv) introducing a

global constraint induced by the surface of

revolution on how all pairs of mended fragments are

coming together as one global mended vessel; and

finally (v) we run a comparative analysis between

our automatic mending method with that of an

Liu Z., Cohen F. and Taslidere E..

Reconstructing Archeological Vessels from Fragments using Anchor Points Residing on Shard Fragment Borders.

DOI: 10.5220/0004231800800083

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 80-83

ISBN: 978-989-8565-48-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

expert manually mending the pieces both in terms of

time and performance. We found that compared to

expert mending, the automatic mending process on

the 313 fragments took about 59 seconds for the

mending plus approximately 60 minutes for the

fragments to be 3D scanned as compared to 12 hours

for stitching by the experts.

2 ALIGNMENT WITH ANCHOR

POINTS

There are several geometrical landmarks, for

instance, inflection points, corner points, and zero-

torsion points, that are intrinsic and preserved under

a rigid transformation. These are the anchor points

that we use in this paper for mending the fragments.

These anchor points are theoretically pinned in the

differential geometry of curves via the Frenet

Frames (Kühnel, 2006).

2.1 Constructing Absolute Invariants

Since length is preserved under 3D rigid maps and

are absolute invariants, we can construct a sequence

of absolute invariants by considering the sequence of

length of lines between the two consecutive anchor

points (e.g., lines between points #1-2, points #2-3,

etc. as shown in Figure 1). Note that there is an

anchor point missing between points #4 and #5 on

curve



. This will not affect the matching given that

there is enough number of anchor points. For a curve

with n anchor points, the sequence of length is

denoted by  



,



,…,



. For the curve 



Figure 1, there are 7 anchor points on the curve.

Figure 1: Absolute invariants with anchor points with

some possibly missing. The algorithm in section 2.3 will

always find the longest matching string.

Thus there are 6 lines. When curve 



undergoes a

rigid transformation (















), the transformed

lines sequence has also the same number of elements











,





,…,





 as the original curve 



. And

we need to find the sequences of elements in that

invariant vectors in  and 



that correspond.

Towards that end we introduce a “longest string

search” technique, which is similar to the “list-

matching algorithm” (Bratko, 1990) for establishing

the correspondence and declaring the match. In

order to recover the rigid transformation and mend

the fragments, at least three pairs of matched points

is required, i.e., the minimum edge string length

should be 2.

Figure 2: Fragment mending based on anchor points (red

dots).

2.2 Longest String Match

As the anchor points and the joining edges between

them are ordered, we can find the longest string of

consecutive edges that lie on two fragments whose

respective length absolute invariants match. This is

necessary as invariant values on two different

fragments coming from different vessels may be

equal to within our allowable error (2-5%) if

considered individually and not as a string. A set of

two or more consecutive anchor points and their

corresponding invariants are considered to be a

“string” (e.g., the set ,1,2,… on one

fragment and the set ,1,2,… on another

fragment). We allow for a small error % (2-5%) in

the values of the invariants, to declare matching

edges in that string search. The sets ,1,

2, …  and ,1,2,… of anchor points are

declared as matching if |

















|0.05∙







for every pair in the two sets. In case that there are

ReconstructingArcheologicalVesselsfromFragmentsusingAnchorPointsResidingonShardFragmentBorders

missing points, for example, in Figure 1, 









then the distance 





will be discarded and the

distance between points 4



and 6



will be calculated,

then 













. Generally speaking, if we encounter

an “unmatched” segment, we will always jump over

one point and check its next anchor point. As this

process is recursive we can deal with more than one

missing point.

The rigid transformation 







,



can be

recovered from three pairs of matched points, or

estimated from more matched anchor points using a

least square error (LSE) estimation method

(Umeyama, 1991).

Once the transformation parameters are found,

the fragments are mapped into the same coordinates

system by undoing the rigid transformation and the

fragments are aligned through their common curve

segment.

Figure 3: With/without global optimization.

2.3 Global Optimization

The mending described in the previous section and

shown in Figure 2 is a pair wise mending process. It

is conceivable that alignment errors will accumulate,

rendering the reconstruction result less than

satisfactory (See right hand side of Figure 3). For

vessels that are axially symmetric, this problem can

be solved by adopting the surface of revolution as a

global constraint. The surface of revolution is

obtained by going through the following steps:

1. Extract the “profile curve” (Willis, Orriols et al.

2003).

2. Obtain the symmetry axis (revolution axis).

3. Rotate the profile curve about the axis.

4. Generate a rotation surface.

5. Use the surface as a global optimization “basis”.

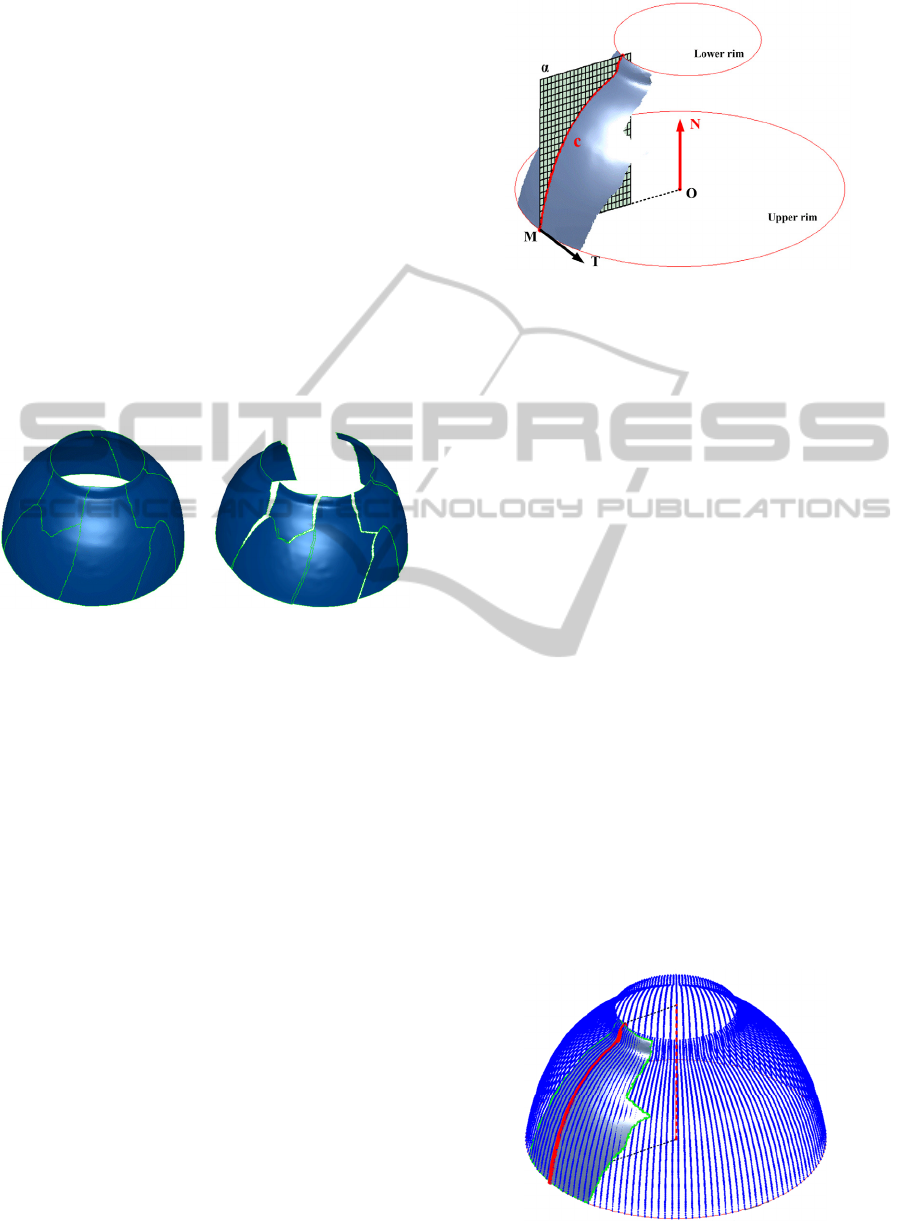
Steps 1 and 2 are shown in Figure 4. The lower rim

and upper rim are obtained by fitting a circle to the

fragment border segments. Of all the fragment

border segments, the one with the smallest fitting

error is the rim. M is a point on the rim. T is the

tangent vector of the upper rim at M. We can find a

plane α that is orthogonal to T and containing M.

Figure 4: Obtain profile curve and symmetric axis.

The cross-section curve c is the profile curve.

Steps 3 and 4 are shown in Figure 5. Here we

rotate the profile curve about the revolution axis to

generate a set of curves which constitute the rotation

surface. This rotation surface is used in our mending

process as a basis shape, where the fragments are not

only aligned to each other, but are also aligned to

this surface. With this global optimization

constraint, the result is improved as shown on the

left hand side of Figure 3.

Note that before a basis shape is found,

fragments with no upper and lower rims are set

aside, and only fragments that do possess both rims

are found and possibly mended using the pair wise

invariants approach. After we obtain a mended

fragment with both upper and lower rims, we extract

the profile curve and the rotation surface (steps 1-5).

We then improve on the mending for all fragments

using the basis shape as a global constraint.

3 EXPRIMENTS

Excavated shards are scanned using a Konica

Minolta Vivid 910 3D scanner. The scanned raw

data (discrete 3D points) is represented as triangle

mesh.

Figure 5: Generate a rotation surface.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

We define the residual error for each fragment as the

mean point-to-point distance map between the

mended fragments and the original unbroken jar.

The mean distance is normalized against the

resolution of the scanner. In all our experiments, the

19 vessels were scanned prior to breaking them into

fragments, with the latter being also scanned

individually.

The described method is tested on 313 fragment

pieces coming from 19 different ceramic objects.

Each fragment is scanned separately.

The mending process for one object is shown in

Figure 2 with all the anchor points showing for two

mended pieces on the vessel. A total of 245 out of

313 fragments were mended properly to their correct

vessels as shown in Figure 6. There were 68 pieces

that could not be mended (See “The Remaining

Pieces” subplot on the upper left of Figure 6) due to

insufficient anchor points.

The entire mending process took 59 seconds on

an Intel i7 processor PC with 18 GB memory for the

mending process, and approximately 60 minutes for

the scanning. This is to be compared to 12 hours for

the stitching done by the experts.

80% fragments were properly mended with

distance map errors at or below the scanner

resolution, i.e. the residual errors normalized by the

scanner resolution were all below or close to 1.

4 CONCLUSIONS

We present a methodology to mend fragments into

vessels based on anchor points on fragment borders.

This work is part of a collaborative project for which

the main objective is to develop and utilize novel

computer vision technology to assist in the

reconstruction of ceramic artifacts recovered from

an excavation site. The work has focused on the use

of one aspect (fragments borders) amongst many

embedded in the fragments. This, in conjunction

with many other aspects such as markings, texture,

or surface information, could be collectively used as

enabling technology helping in the mending process.

This is particularly important if the extracted anchor

points in the paper are absent due to complete

erosion of the fragments borders on abutting

fragments, which would limit the success of such a

method. The whole project as an application of

computer vision in archaeology is unique as an

enabling technology for timely analysis,

interpretation, and presentation of history evidence.

It is also considered as a great need by the U.S.

Department of the Interior National Park Service.

Figure 6: Mended objects.

ACKNOWLEDGEMENTS

This work is supported by the National Science

Foundation IRIS Division under grant #0803670.

REFERENCES

Bratko, I. 1990. Prolog Programming for Arificial

Intelligence. London, UK, Addison Wesley.

Kühnel, W. 2006. Differential geometry : curves - surfaces

- manifolds. Providence, R.I., American Mathematical

Society.

Papaioannou, G. and E. A. Karabassi 2003. "On the

automatic assemblage of arbitrary broken solid

artefacts." Image and Vision Computing 21(5): 401-

412.

Rodriguez, W., M. Last, et al. 2004. "3-Dimensional curve

similarity using string matching." Robotics and

Autonomous Systems 49(3-4): 165-172.

Ucoluk, G. and I. H. Toroslu 1999. "Automatic

reconstruction of broken 3-D surface objects."

Computers & Graphics 23(4): 573-582.

Umeyama, S. 1991. "Least-Square Estimation of

Transformation Parameters Between Two Point

Patterns." IEEE Transactions on Pattern Analysis And

Machine Intelligence 13(4): 376-380.

Willis, A., X. Orriols, et al. 2003. Accurately Estimating

Sherd 3D Surface Geometry with Application to Pot

Reconstruction. CVPR Workshop: ACVA. Madison,

WI, USA, IEEE Computer Society.

ReconstructingArcheologicalVesselsfromFragmentsusingAnchorPointsResidingonShardFragmentBorders