Dominant Frequency, Regularity and Organization Indexes Response

to Preprocessing Filter Variations on Simulated Electrograms

During Atrial Fibrillation

Andr´es Orozco-Duque

, Juan P. Ugarte

, Catalina Tob´on

2,3

, Carlos A. Morillo

, Javier Saiz

and John Bustamante

Centro de Bioingenier´ıa, Universidad Pontiﬁcia Bolivariana, Medell´ın, Colombia

Grupo de Bioelectr´onica, i3BH, Universidad Polit´ecnica de Valencia, Valencia, Spain

Instituto Tecnol´ogico Metropolitano, Medell´ın, Colombia

Arrhythmia & Pacing Service, Department of Medicine, McMaster University-HHSC-PHRI, Hamilton, Canada

Keywords:

Atrial Fibrillation, Dominant Frequency, Electrograms, Organization Index, Regularity Index, Digital Filters.

Abstract:

Atrial ﬁbrillation (AF) is the most common tachyarrhythmia. An accurate AF diagnosis is based on electro-

grams (EGM) interpretation. In this work, we evaluated different preprocessing ﬁlters to calculate dominant

frequency (DF), organization index (OI) and regularity index (RI) for EGM during AF, this comparative analy-

sis has not been reported previously. EGM were obtained from AF simulated by a three-dimensional model of

human atria. The preprocessing stage with a low-pass ﬁlter, rectiﬁcation and high pass ﬁlter was implemented.

Additionally, a test over 60 simulated signals using different ﬁlters with different orders was developed. It was

found that some ﬁlters affect the DF calculation and cause a bimodal distribution in the DF histogram. Cal-

culation of DF, OI and RI by Fast Fourier Transform analysis of preprocessing signals has high sensibility to

ﬁlters settings. OI and RI analysis works properly in EGM with single potentials, however, DF is not necessary

related with cycle length in fragmented EGM and OI calculation becomes inaccurate with high DF.

1 INTRODUCTION

Atrial ﬁbrillation (AF) affects about 2% of the pop-

ulation and its incidence is increasing. The AF is

characterized by rapid and chaotic electrical activity

over the atria without the ability to generate effec-

tive atrial contraction. The accurate AF diagnosis is

based on the interpretation of electrograms (EGM)

recroded from different atrial zones. Cardiovertion,

antiarrhythmic drugs and radiofrequency ablation are

used like therapeutic methods in AF. Ablation could

be improved with techniques of cardiac mapping ob-

tained from intracardiac EGM recorder on atrial tissue

in order to ﬁnd areas with arrhythmogenic substrate.

Thus, it is necessary to found a relationship between

electrical propagation and EGM; however this is not

entirely resolved.

Recent studies focus on the location of complex

fractionated atrial electrograms (CFAE) as AF sub-

strates looking for the ablation of these areas, spe-

cially for chronic AF, however nowadays this is an

open problem. In order to ﬁnd the relation between

EGM and electrical propagation, some indexes

have been developed, attempting to measure spatio-

temporal organizationof AF, which is related to repet-

itive morphology and high periodicity of the signals.

To measure the extent of spatial organization of

atrial activation during AF, ()Botteron1995 proposed

a preprocessing method for EGM. This is described

as follows: First, Band-passed ﬁltering with digital,

zero phase, third-orderButterworth ﬁlter with cut-offs

of 40-250Hz. Second, Absolute value (rectiﬁcation).

Third, Low-pass ﬁlter with Butterworth ﬁlter with

cut-off of 20 Hz. This method has been used since

1995 to calculate different indexes: the dominant fre-

quency (DF), organization index (OI) and regularity

index (RI) (()Everett2001). (Everett et al., 2001) de-

termined that to improve the Fast Fourier Transform)

FFT performance in the preprocessing stage is neces-

sary to use 4s or greater windowed signals.

DF, OI and RI are currently being used in clin-

ical practice. However different authors have dis-

cussed the practical use of these indexes, because they

are sensitive to the method of recording, signal-to-

306

Orozco-Duque A., P. Ugarte J., Tobón C., A. Morillo C., Saiz J. and Bustamante J..

Dominant Frequency, Regularity and Organization Indexes Response to Preprocessing Filter Variations on Simulated Electrograms During Atrial

Fibrillation.

DOI: 10.5220/0004231903060309

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 306-309

ISBN: 978-989-8565-36-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

noise ratio (SNR), far ﬁeld ventricular depolarization

or complexity of the signal ((Elvan et al., 2009)). In

this work, the sensitivity of these indexes was studied

when the ﬁlters are setting in different ways in pre-

processing stage and DF, OI and RI calculation was

analyzed during CFAE.

2 METHODS

2.1 Atrial Fibrillation and Electrograms

A chronic AF episode was simulated in an anatomi-

cally realistic 3D model of human atria that includes

ﬁbers orientation, electrophysiological heterogeneity

and anisotropy. Unipolar atrial EGM at 60 points of

the left atrial surface (0.2 mm from the surface) were

simulated each millisecond during 8 seconds (Tob´on

et al., 2010).

2.2 Dominant Frequency, Organization

and Regularity Indexes

The DF was calculated using the deﬁnition given by

(Everett et al., 2001), DF is the maximum peak in

the power spectrum after apply a FFT with hamming

window to the output of preprocessing stage deﬁne by

(Botteron and Smith, 1995).

OI (Everett et al. 2001) is the ratio between the

area under DF ±0.75Hz including the areas under

harmonic frequencies to DF between 3 to 20Hz and

the total area as shown in the following equation:

OI =

A(DF ± 0.75) +

∑

i=2

A[(DF ∗ i) ± 0.75]

A(3 Hz to 20 Hz)

(1)

where A is a function that calculates the area and

the harmonics are include only if the peak is less than

20Hz.

We use the RI index deﬁned by (Sanders et al.,

2005) like the ratio of spectral power in a 0.75Hz band

centered at the DF and the total power between 3Hz

and 20Hz.

3 RESULTS

The preprocessing method was tested with four differ-

ent types of ﬁlters, with different orders, implemented

in MatLab

. Butterworth, Chebyshev 1, Chebyshev

2 and elliptic ﬁlters were used. Low-pass ﬁlters be-

tween 2nd-order to 20th-order and band-pass ﬁlters

between 4th-order to 40th-order were used. In each

combination the band-pass order was twice the order

of low-pass ﬁlter.

Figure 1 shows the histogram of DF calculation

when were applied 76 combinations ﬁlters to the 60

simulated signals. The histogram shows that DF are

mainly concentrated between 5.5 Hz and 6.5 Hz, how-

ever there are results between 11 and 13 Hz wich cor-

respond to DF of ﬁve signals with high degree of frag-

mentation and with some speciﬁc ﬁlters.

4 6 8 10 12 14

Frequency (Hz)

Repetitions

Figure 1: General histogram of DF calculation with76 com-

bination ﬁlter applied to 60 EGM signals.

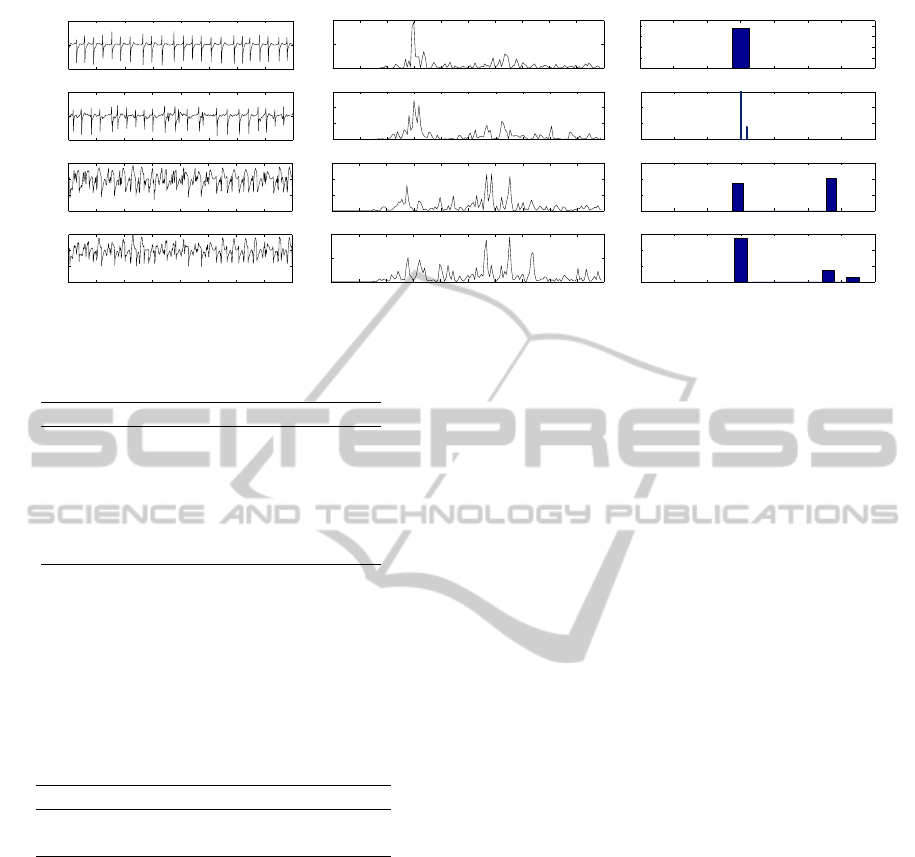
Figure 2 shows four AF signals with their respec-

tive spectrum and DF histogram. The signal in Fig-

ure 2(a) is a regular EGM with single potential, DF

calculation had the same result for each combination

of ﬁlters, as seen in its histogram. Figure 2(b) shows

two DF results depending on the used ﬁlters, however,

the difference between them is barely 0.33 Hz. Fig-

ure 2(c) and 2(d) are CFAE signals corresponding to

particulars combination of ﬁlter resulted in high DF,

greater than 10Hz. Their power spectrums correspond

to the set with high DF. These results show that re-

sponse of DF analysis on CFAE signals is sensible to

ﬁlters conﬁguration.

2nd-order ﬁlters or higher than 6th-order ﬁlters in

the low pass stage results in low DF in CFAE sig-

nals, consequently there is no relation between DF

and CFAE signals. Also the relation between DF and

cycle length is not clear. 3rd-Order and 4th-order But-

terworth, Chebyshev 1 and Chebyshev 2 ﬁlters pro-

duced high DF in CFAE signals, which is appropri-

ated if it is looking for a relation between DF and

CFAE.

Table 1 shows the DF, OI and RI means for all

ﬁlter combinations applied to signals showed in ﬁg-

ure 2. EGM 2(c) and EGM 2(d) were separated in

two sets, according to DFs value showed in their his-

tograms. The variation of DF values yields a varia-

tion of OI and RI. In signals where DF > 10 Hz are

not possible to calculate OI because the harmonicsare

greater than 20Hz.

Figure 3(b) shows the power spectrum of the pre-

processing EGM for an AF signal with CFAE using

DominantFrequency,RegularityandOrganizationIndexesResponsetoPreprocessingFilterVariationsonSimulated

ElectrogramsDuringAtrialFibrillation

307

0 0.5 1 1.5 2 2.5 3 3.5 4

−5

(a)

T ime (s ec)

Amp . ( mV)

0 2 4 6 8 10 12 14 16 18 20

0.05

0.1

Fr e que nc y (Hz )

Powe r

0 2 4 6 8 10 12 14

Fr e que nc y (Hz )

Re p et i ti ons

0 0.5 1 1.5 2 2.5 3 3.5 4

−5

(b)

T ime (s ec)

Amp . ( mV )

0 2 4 6 8 10 12 14 16 18 20

0.02

0.04

0.06

Fr e que nc y (Hz )

Powe r

0 2 4 6 8 10 12 14

Fr e que nc y (Hz )

Re p et i ti ons

0 0.5 1 1.5 2 2.5 3 3.5 4

−10

−5

(c)

T ime (s ec)

Amp . ( mV )

0 2 4 6 8 10 12 14 16 18 20

0.02

0.04

0.06

Fr e que nc y (Hz )

Powe r

0 2 4 6 8 10 12 14

Fr eq u en c y ( H z )

Re p et i ti ons

0 0.5 1 1.5 2 2.5 3 3.5 4

−10

−5

(d)

T ime (s ec)

Amp . ( mV )

0 2 4 6 8 10 12 14 16 18 20

0.02

0.04

Fr e que nc y (Hz )

Powe r

0 2 4 6 8 10 12 14

Fr e que nc y (Hz )

Re p et i ti ons

Figure 2: Four different EGM, their respective power spectrum and histogram.

Table 1: DF, OI and RI for signals showed in ﬁgure 2.

DF (Hz) OI RI

EGM 3a 5.98 0.45 0.35

EGM 3b 6.06 0.43 0.35

EGM 3c-set1 11.72 – 0.17

EGM 3c-set2 5.48 0.36 0.18

EGM 3d-set1 5.66 0.34 0.15

EGM 3d-set2 11.84 – 0.14

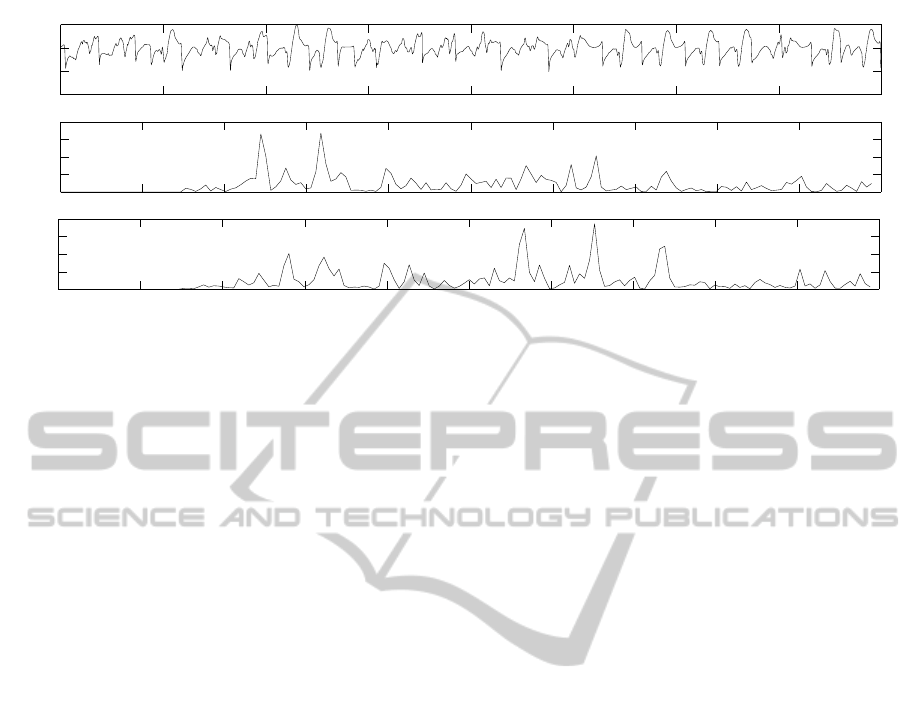
a 2th-order Butterworth ﬁlter and Figure 3(c), a 4th-

order Butterworth ﬁlter. Figure 3 indicate the sensi-

tivity of the power spectrum when it was changed the

order of the ﬁlter. This causes variations in the max-

imum peak affecting DF, OI and RI values presented

in Table 2.

Table 2: DF, OI and RI for signal showed in ﬁgure 3.

Butterworth DF (Hz) OI RI

2nd-order ﬁlter 6.35 0.26 0.14

4th-order ﬁlter 13.06 – 0.12

4 DISCUSSION

Several authors have used different ﬁlters in the pre-

processing stage, (Everett et al., 2001) used a 2nd-

order butterworth ﬁlters. (Barbaro et al., 2000) used

40th-order FIR ﬁlters, (Nguyen et al., 2009), other

authors used the pre-processing method deﬁned by

(Botteron and Smith, 1995) but they did not deﬁne

the order and type of ﬁlters. The present work has

evidenced for the ﬁrst time the importance of estab-

lishing the type and the order of the band-pass and

low-pass ﬁlters in the pre-processing stage.

DF deﬁnition is based in the results of (Skanes

et al., 1998) who concluded that DF is determined by

the cycle length of AF spatio-temporal periodic activ-

ity. DF greater than 10 Hz resulted from CFAE has

no physiological meaning related with cycle length,

since high frequencies could be related with the com-

plexity of the signal. This is supported by other au-

thors who showed that there is a poor correlation be-

tween the EGM cycle length and DF in patients with

persistent AF ((Elvan et al., 2009)). (Ng et al., 2007)

demonstrated that although DF analysis can be reli-

ably, used to measure local activation rate in ideal sit-

uations, several factors can contribute to the unpre-

dictability of DF analysis related to recording tech-

niques and signal properties. They suggested the use

of well deﬁned signal processing techniques and care-

ful evaluation of the time domain signals.

In CFAE, independently of the ﬁlter used in the

preprocessing stage, DF is not necessary related with

cycle length. Depending on ﬁlters settings, DF could

be related or not with complexity of the EGM, in any

case the DF has no correlation with morphology of

signals. DF by itself could not make any difference

between a CFAE and a high frequencyEGM with sin-

gle potentials. RI deﬁned by (Sanders et al., 2005) as

an auxiliary index to ensure reliability in DF detec-

tion, such that DF calculation is accepted only if RI

> 0.2 in order to reject signals with poor SNR. How-

ever, despite of using simulated free-noise EGM in

present work, results gave RI < 0.2 in some cases,

which correspond to signals with CFAEs. The OI was

deﬁned by (Everett et al., 2001) who showed that this

index has a correlation with the periodicity and mor-

phology of AF signal. However, in CFAE where DF

> 10 Hz, It is not possible to calculate OI because the

harmonics are greater than 20Hz.

As a future work we are testing DF, OI and RI on

different simulated and real tachyarrhythmia signals.

Additionally we are developing other indexes corre-

lated with the morphology of the signals to character-

ize CFAE.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

308

0 0.5 1 1.5 2 2.5 3 3.5 4

−10

−5

(a)

Ti me (sec)

Am p. (m V)

0 2 4 6 8 10 12 14 16 18 20

0.01

0.02

0.03

0.04

(b)

Frequency ( Hz )

Powe r

← FD=6.34

0 2 4 6 8 10 12 14 16 18 20

0.01

0.02

0.03

0.04

(c)

Frequency ( Hz )

Powe r

← FD=13.06

Figure 3: (a). EGM. (b). EGM power spectrum using 2-order Butterworth ﬁlters. (c). signal power spectrum using 4-order

Butterworth ﬁlters.

5 CONCLUSIONS

Calculation of DF, OI and RI by FFT analysis of

preprocessing signal using the (Botteron and Smith,

1995) method has high sensitivity to ﬁlters settings.

Our results suggest that it is necessary to specify the

ﬁlter conﬁguration used in the pre-processing stage in

order to avoid ambiguous results. OI and RI analysis

works properly in EGM with single potentials, how-

ever, DF is not necessary related with cycle length in

CFAE while OI calculation has problems with high

DFs. In order to study CFAE we recommend keep

researching and developing of other analysis tools.

REFERENCES

Barbaro, V., Bartolini, P., Calcagnini, G., Censi, F.,

Michelucci, a., and Morelli, S. (2000). A high-

temporal resolution algorithm to quantify synchro-

nization during atrial ﬁbrillation. Proceedings of

the 22nd Annual International Conference of the

IEEE Engineering in Medicine and Biology Society.,

4:2959–2962.

Botteron, G. W. and Smith, J. M. (1995). A technique for

measurement of the extent of spatial organization of

atrial activation during atrial ﬁbrillation in the intact

human heart. IEEE transactions on bio-medical engi-

neering, 42(6):579–86.

Elvan, A., Linnenbank, A. C., van Bemmel, M. W., Misier,

A. R. R., Delnoy, P. P. H. M., Beukema, W. P., and

de Bakker, J. M. T. (2009). Dominant frequency of

atrial ﬁbrillation correlates poorly with atrial ﬁbrilla-

tion cycle length. Circulation. Arrhythmia and elec-

trophysiology, 2(6):634–44.

Everett, T. H., Kok, L. C., Vaughn, R. H., Moorman, J. R.,

and Haines, D. E. (2001). Frequency domain algo-

rithm for quantifying atrial ﬁbrillation organization to

increase deﬁbrillation efﬁcacy. IEEE transactions on

bio-medical engineering, 48(9):969–78.

Ng, J., Kadish, A. H., and Goldberger, J. J. (2007). Tech-

nical considerations for dominant frequency analy-

sis. Journal of Cardiovascular Electrophysiology,

18(7):757–764.

Nguyen, M., Schilling, C., and D¨ossel, O. (2009). A

new approach for frequency analysis of complex frac-

tionated atrial electrograms. Conference proceed-

ings : 2009 Annual International Conference of the

IEEE Engineering in Medicine and Biology Society.,

2009:368–71.

Sanders, P., Berenfeld, O., Hocini, M., Ja¨ıs, P.,

Vaidyanathan, R., Hsu, L.-F., Garrigue, S., Takahashi,

Y., Rotter, M., Sacher, F., Scav´ee, C., Ploutz-Snyder,

R., Jalife, J., and Ha¨ıssaguerre, M. (2005). Spec-

tral analysis identiﬁes sites of high-frequency activity

maintaining atrial ﬁbrillation in humans. Circulation,

112(6):789–97.

Skanes, a. C., Mandapati, R., Berenfeld, O., Davidenko,

J. M., and Jalife, J. (1998). Spatiotemporal periodic-

ity during atrial ﬁbrillation in the isolated sheep heart.

Circulation, 98(12):1236–1248.

Stiles, M. K., Brooks, A. G., Kuklik, P., John, B., Dim-

itri, H., Lau, D. H., Wilson, L., Dhar, S., Roberts-

Thomson, R. L., Mackenzie, L., Young, G. D., and

Sanders, P. (2008). The relationship between electro-

gram cycle length and dominant frequency in patients

with persistent atrial ﬁbrillation. Journal of cardio-

vascular electrophysiology, 20(12):1336–1342.

Tob´on, C., Ruiz, C., Rodr´ıguez, J., Hornero, F., Ferrero, J.

M. J., and S´aiz, J. (2010). Anatomical realistic 3D

model of human atria. Application to the study of vul-

nerability to atrial arrhythmias. Supplement to Heart

Rhythm, (75S):S289–S290.

DominantFrequency,RegularityandOrganizationIndexesResponsetoPreprocessingFilterVariationsonSimulated

ElectrogramsDuringAtrialFibrillation

309