
Evolution of Cooperation in Packet Forwarding with the Random
Waypoint Model
Jeffrey Hudack
1,2
, Nathaniel Gemelli
1,2
and Jae Oh
1
1
Syracuse University, Syracuse, NY, U.S.A.
2
Air Force Research Laboratory, Rome, NY, U.S.A.
Keywords:
Game Theory, Evolutionary Games, Ad Hoc Networks, Mobility Models.
Abstract:
In multi-agent systems with self-interested individuals interacting locally, it can be difficult to determine if
cooperative behavior will emerge. Evolutionary Game Theory provides some valuable tools to this end, but
is not suited to systems with dynamic models of interaction. Mobile ad hoc networks provide a compelling
application for evolutionary game theory, but there are still significant gaps between the theoretical results and
the practical challenges. We discuss and provide some of the assumptions necessary to apply previous work
in evolutionary game theory to the ad hoc network packet routing domain. We then analyze the similarities
and differences between Brownian mobility and Random Waypoint mobility and show that convergence to
cooperation requires a significant reduction in velocity for the Random Waypoint model. Our contribution is
to provide evidence that more realistic mobility models can make convergence to cooperation more difficult
than previously shown using random methods.
1 INTRODUCTION
Evolutionary game theory has emerged as a useful
framework for understanding the emergence of coop-
eration in populations of inherently selfish individu-
als. These abstract models and metaphors have been
combined with a consistent methodology to analyze
problems that are common across a wide range of ap-
plications including biology, sociology, physics, and
computer science. In general, evolutionary games
provide a means to model complex adaptive systems
with evolving individual and collective behavior.
One of the most well-known and studied games is
the Prisoners’ Dilemma, (PD) (Axelrod, 1992) a sym-
metric, two-player game in which individuals must
choose between cooperation (C) and defection (D).
In this game, cooperation is at a disadvantage and a
rational player will always defect in one-shot play. In
fact, defection has been shown to be the Nash equilib-
rium pure strategy (Axelrod, 1992). This game struc-
ture is a metaphor for many types of interactions, in-
cluding ad hoc network packet forwarding. (Nisan,
2007)
Mobile ad hoc networks (MANETs) are multi-
hop, wireless networks where each node is both a
client and a router, and direct communication is lim-
ited by geographic distance. MANETs are character-
ized by a population of agents with a series of pair-
wise interactions, making it an ideal application for
evolutionary game theory. The performance of these
networks is dependent on both the level of activity
and the components’ ability to adapt to changes in the
network. Simple and lightweight approaches to local
decision making can reduce the effects of mobility on
the routing overhead (Viennot et al., 2004). We show
the properties of the Random Waypoint Model with
respect to Brownian motion and then explore effects
of mobility on the evolution of cooperation.
For a population of individuals playing a PD
game, cooperative behavior has been shown to evolve
based on the graph structure, interaction models, and
strategy evolution mechanisms. Certain properties
of the graph promote cooperation, such as scale-
free networks (Boccaletti et al., 2006) and a high
clustering coefficient (Assenza, 2008). Additionally,
other works such as (Poncela et al., 2008) and (Szol-
noki et al., 2008) have explored preferential attach-
ment models and (Helbing and Yu, 2009) uses graph
rewiring mechanisms to promote cooperation. Re-
cent work has shifted to more realistic models of
rewiring based on dynamic spatial models (Meloni
et al., 2009). In these models individuals interact
based on their locality and move through the environ-
ment and, as a result, the partners that an agent in-
58
Hudack J., Gemelli N. and Oh J..
Evolution of Cooperation in Packet Forwarding with the Random Waypoint Model.
DOI: 10.5220/0004234800580066
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 58-66
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

teracts with is often repeated for some length of time
before changing.
Prior work showing the effects of interaction mod-
els used random selection (Oliphant, 1994), random
initial selection with fixed neighbors (Cohen et al.,
1999), or grid-based environments where agents are
limited to interaction in a finite set of locations in the
space, as found in (Poncela et al., 2008), (Szolnoki
et al., 2008) and (Helbing and Yu, 2009). While these
discrete representations are convenient for reducing
the complexity of the simulation they do not often
model practical scenarios. More recent work has ex-
plored simple mobility models for changing interac-
tions, such as Brownian motion, that do not emulate
the motion that would be expected from individuals
moving in the real world (Johnson and Maltz, 1996).
The main contribution of this work is the appli-
cation of random waypoint (RWP) mobility to evo-
lutionary game theory with a graph-based interaction
model. This extends prior work with a more realistic
representation of agent movement that better reflects
the expected behavior of a mobile ad hoc network.
We show that the RWP model has significant effects
on the evolution of cooperation among a population
of mobile, self-interested agents.
In Section 2 we will discuss how the Prisoners’
Dilemma can be used as a packet forwarding interac-
tion model between pairs of agents. In Section 3.1 we
will discuss the process for choosing pairs of agents
to interact as a function of communication distance.
In Section 3.2 the method and justification for evo-
lution of individual agent strategies will be provided.
Section 4 discusses the mobility model that motivates
the primary contribution of this work. Finally, we will
provide our simulation parameters and results in Sec-
tion 5 and discuss the implications of our findings in
Section 6.
2 PACKET FORWARDING GAME
A wireless ad hoc network is a decentralized network
without a fixed infrastructure to facilitate routing of
packets. Every node is both a client and a router
and the functionality of the network relies on each
node to cooperate. In scenarios where the nodes are
self-interested, each node in the network participates
(or chooses not to participate) in forwarding pack-
ets across the network to allow for communication
between end points. In this environment, network
nodes must choose between forwarding (C) and not
forwarding (D) packets that are being routed through
them.
Due to a lack of a routing infrastructure, flood-
Figure 1: Normal form reduced Prisoners’ Dilemma game
with single parameter b as the benefit of defection.
ing in mobile ad hoc networks (MANETs) has been
shown to be an effective method of communication
(Ho et al., 1999). Flooding is defined as a mech-
anism where each node rebroadcasts a message m
once when it is received, then ignores m if it received
again. As a result, messages are diffused across the
network and result in many pairwaise interactions be-
tween neighboring nodes. We model this interaction
using a game theoretic framework.
The Prisoners’ Dilemma is a nonzero-sum, non-
cooperative, two-player game. In this game R is the
payoff for mutual cooperation, T is the temptation to
defect, S is the ”suckers” payoff, and P is the pay-
off for mutual defection. We use the reduced form
as defined in (Nowak, 1992) with the payoff values
R = 1,T = b(b > 1), S = P = 0, shown in Figure 1.
This simple model allows us to analyze the effects of
the mobility model with respect to a single parameter
b representing the benefit of defection. More complex
models of interaction for packet forwarding in ad hoc
networks exist (Kamhoua et al., 2010), but the addi-
tional parameters required would make it difficult to
focus solely on the effects of mobility.
When both neighbors cooperate all packets are
forwarded. Defection can be attractive when neigh-
bors cooperate for a number of reasons. A self-
ish agent can conserve battery life, CPU cycles, or
available network bandwidth while relying on its own
packets to be forwarded. This type of selfish behav-
ior by a small percentage of nodes in the network
has been shown to have significant negative impact on
network communication (Tanachaiwiwat et al., 2004).
More importantly, when an agent is interacting with
many defectors there should be a mechanism to cease
cooperation so not to be taken advantage of.
Each node would benefit to have its own packets
forwarded and relies on its neighbors to do so. How-
ever, there are complications that arise when the pack-
ets are not originating from the neighboring agent but
rather being forwarded from another agent. Assuming
agents are able to monitor the behavior of their neigh-
bors, an agent considering defection runs the risk of
having a neighbor witness this non-cooperation and
EvolutionofCooperationinPacketForwardingwiththeRandomWaypointModel
59

retaliate in the future. However, if a packet originates
from a non-neighbor source then the forwarding agent
has no motivation to retaliate against a neighboring
defector. In order to bound our analysis to pairwise
interactions between nodes we must address this dis-
parity.
One method for handling a mixture of direct and
indirect packets is a stochastic game in which the cost
of defection is different for each packet type. For-
tunately, we can use the probability distribution of
direct and indirect packets, along with their respec-
tive costs for defection, to form a single normal form
game that will yield the same behavior over a large
number of interactions. A simpler model for dealing
with indirect packets is to assume that there is a com-
munity enforcement mechanism that requires nodes
place as much value on forwarding others’ packets as
it does its own (Kamhoua et al., 2010). Using this
mechanism, a defecting agent can expect to be pun-
ished equally for failing to forward any packet, re-
gardless of where it originated. Both methods yield a
normal form game that is sufficient for capturing the
nature of the packet forwarding interactions.
3 EVOLUTIONARY GAMES
Evolutionary game theory (EGT) is the application of
game theory to populations of individuals. These in-
dividuals can be biological life forms in an ecosys-
tem, particles interacting to form compounds, or au-
tomated systems that exhibit an emergent behavior.
While game theory focuses on the interactions be-
tween a specific pair of individuals, EGT provides
a set of mechanisms for repeated interactions among
members of a population. As a result, complex pat-
terns and behaviors can emerge from relatively simple
individual strategies.
Evolutionary games can be characterized by three
components: a game, an interaction model, and strat-
egy evolution mechanisms. We have already dis-
cussed the packet forwarding game in the previous
section, which will be our focus in this work. The in-
teraction model determines how agents are paired to
play an instance of the game at each time step, and is
discussed in the next section. Then, we will describe
the strategy evolution mechanism, which is used by
individuals to change their strategy based on the out-
comes of the interactions in a time step.
3.1 Interaction Model
We model interactions between agents as a graph with
vertices representing individuals and edges indicating
pairwise interaction at each time step. Unlike Erd
¨
os-
Renyi graphs, where agents are paired randomly with
some probability, the agents are given a random loca-
tion in the space and an edge is formed based on their
locality.
Consider a graph where nodes are placed in a d-
dimensional space R
d
, with edges existing only be-
tween nodes that are close to each other. A geometric
graph G(V,r) is an undirected graph with V ⊂ R
d
as
the set of vertices.For this work we consider point in
2 dimensional space with V ⊂ R
2
. The set of edges is
defined as E = {(u,v)|(u,v ∈ V )∧(0 <k u −v k≤ r)},
where k · k is the distance norm on two points (x
1
,y
1
)
and (x
2
,y
2
). We use the `
2
-norm, or Euclidean dis-
tance, defined as
p
(x
1
− x
2
)
2
+ (y
1
− y
2
)
2
.
To simplify analysis, we will assume that all ver-
tices are normalized to have the same radius r = 1 and
are in a toroidal space. A toroidal model is chosen to
remove the border effects on the degree of vertices.
The initial configuration corresponds to a random ge-
ometric graph (Penrose, 2003) with the topology de-
pending on the number of agents N and the length of
the space L. The density of the agents ρ = N/L
2
has a
direct effect on the connectivity of the graph and the
component size. We represent the degree of node i at
time t as k
i
(t).
There is a very large body of work in evolutionary
Prisoners Dilemma that makes use of round-robin in-
teraction in a population (Kendall et al., 2007). While
the round-robin approach is ideal for generating ran-
domized, well-mixed interactions, it does not con-
sider the types of spatial interactions that are observed
in ad hoc networks. The spatial model has a signifi-
cant effect on game play because of the dependence
of edges. For example, assume a population of 1000
nodes where a pair of nodes A and B are neighbors
and C is also a neighbor to B. Because A and B, and
B and C, are related based on distance there is a higher
likelhood that C will be a neighbor of A as opposed to
another arbitrary node being a neighbor of A. This de-
pendency on interactions can contribute to the forma-
tion of clusters of cooperation, as discussed in Section
4.
At each simulation time step agents interact with
all of their neighbors and keep track of the payoffs
received. In the context of mobile ad hoc networks,
this behavior is analogous to multicast communica-
tion. While there exist routing protocols for ad hoc
networks that allow direct addressing of packets, it
has been shown that there is a threshold of mobility
at which maintaining the routing paths is difficult and
multicast flooding is the most reliable method of de-
livery (Ho et al., 1999). Knowledge of the forwarding
behavior of a neighbor is made possible by watchdog
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
60

mechanisms (Marti et al., 2000) and observation of
transmissions made by neighboring nodes.
3.2 Evolution of Strategies
As agents interact with their neighbors they may de-
termine that it is in their best interest to change their
behavior to increase their individual payoff in future
interactions. One methodology for adjusting behav-
ior is to adopt a method of replication by imitation
(Weibull, 1997). Using this method agents observe
the payouts received by other agents and decide if
they wish to adopt that strategy as their own in the
future. For mobile ad hoc networks it makes sense
to limit any observations to neighboring agents, al-
though in some environments it could be argued that
no information is available regarding the payouts re-
ceived by other agents.
In the interest of being consistent with prior work
in the evolution of cooperation on mobile networks
we adopt the payoff monotone replication function
described in (Poncela et al., 2009). At each time step
an agent i, with degree k
i
(t) at time t, chooses an
agent j, with degree k
j
(t) at time t, at random from
its neighbors. Let the total payoffs received by these
agents in the current time step t be f
i
(t) and f
j
(t), re-
spectively. If f
i
(t) ≥ f
j
(t) then agent i keeps its cur-
rent strategy. If f
i
(t) < f
j
(t) then agent i adopts agent
j’s strategy with probability
P
i
=
f
j
(t) − f
i
(t)
b · max{k
i
(t),k
j
(t)}
(1)
This update is done synchronously for all agents
at the end of each time step, after they have com-
pleted their interactions with their neighbors and re-
ceived the associated payoffs. After all of the agents
have completed their strategy update the total payoffs
are reset to zero.
4 MOBILITY MODEL
Much of the previous work analyzing the effects of
mobility models on the evolution of cooperation uses
lattice or grid-based models, such as (Perc and Szol-
noki, 2008) and (Helbing and Yu, 2009). While this
approach provides a useful simplification of the space
of interaction, it constrains interaction to adjacent grid
locations and limits the opportunities for movement.
Some recent work explores a continuous 2D space
with a Brownian motion model (Meloni et al., 2009),
which is well-suited to modeling the random motion
of particles in physics. However, because we seek
to model mobile devices held by persons with inten-
tional movement our analysis requires a more appro-
priate mobility model.
Random Waypoint (RWP) (Johnson and Maltz,
1996) mobility is a widely used model for simulat-
ing mobility in ad hoc networks. It was designed to
emulate the movement patterns of mobile users and
devices and includes parameters for location, direc-
tion, velocity. At the initial time step each node is
assigned a random location in the space and a ran-
dom waypoint representing the destination. Given a
velocity v, at each time step the mobile nodes move a
distance v directly towards their destination waypoint.
Upon reaching the destination the node will pause for
p time steps, randomly generate a new waypoint, and
then continue movement towards the new destination.
In this work we set p = 0.
Unlike the Brownian motion model, the group-
ings of nodes are much more ‘volatile’, meaning that
nodes that are near each other are highly likely to
seperate as time passes. The implications of this
model on the evolution of cooperation are signifi-
cant. Because individual cooperation relies on neigh-
bors also cooperating, the population will often form
regions of cooperation that can withstand defection
(Nowak, 1992), as shown in Figure 2. With a Brow-
nian motion model these pockets are relatively sta-
ble and nodes will remain within relatively close dis-
tance of each other. When using RWP nodes are often
moving along a vector and will move in and out of
cooperation regions, adapting to their current neigh-
bors as they pass. As a result, regions of coopera-
tion are often unstable because the cooperating neigh-
bors are unlikely to be nearby for very long. This
requires regions of cooperation that are large enough
to withstand the constant churn of individuals passing
through them.
Even though the RWP mobility paints a grim pic-
ture of the potential for cooperation there are still
conditions under which cooperation can flourish and
the population will converge. In the next section we
present the details of our simulation and provide the
parameters that will encourage cooperation in a large
population of mobile devices.
5 SIMULATION AND RESULTS
Simulations were created using the MASON multi-
agent simulation developed at George Mason Uni-
versity (Luke et al., 2005) and using the included li-
braries for 2D continuous toroidal space. MASON
was chosen because it is a lightweight environment
that allowed for rapid development of simulations
EvolutionofCooperationinPacketForwardingwiththeRandomWaypointModel
61

Figure 2: A snapshot of a simulation run exhibiting clus-
ters of cooperation. Cooperators (green) rely on cooperat-
ing neighbors to receive sufficient payouts that discourage
changing their strategy to defection (red).
with 10
3
agents over many runs.
We make some assumptions for simulation that
may or may not be an accurate depiction of real world
conditions. We model the mobile agents as point
objects in a 2 dimensional toroidal space and have
them interact whenever they are within radius r = 1
of each other. The toroidal space removes edge con-
ditions and is meant to represent a sampling of a larger
space. While the interactions wrap around the edge,
we feel the number of agents is sufficient to avoid
agents experiencing feedback effects from their own
actions. Finally, the strategy evolution relies on an
agent having information about the payoffs received
by its neighbors. While it’s feasible that an agent may
have this information, it is not necessarily true in all
situations.
We first compare the dynamic properties of RWP
and Brownian mobility using two standard metrics:
link change rate (LCR) and link density (LD) (Cho
and Hayes, 2005). LCR (Equation 2) is the average
rate of change of edges on the graph and is computed
as the sum of edges added and removed per time step.
LD (Equation 3) is measured as the average number
of time steps a link is maintained and measures the av-
erage time agents spend linked with the same neigh-
bors. For the set of agents A, velocity v, and time
of simulation t < T , let E
A
(t) and E
R
(t) be the edges
added and removed at time t, respectively, with E
i
A
(t)
and E
i
R
(t) returning only those edges for agent i. E
T
is the set of all edges in the simulation and D(e) is
the duration of one instance of a specific edge. We set
a density value of ρ = 1.3 to remain consistent with
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.0035 0.004 0.0045 0.005
LCR
v
Brownian
Waypoint
Figure 3: Link change rate (LCR) for the Brownian and
RWP mobility models with respect to velocity for N = 10
3
,
ρ = 1.3. In general, the RWP mobility has a slightly larger
rate of change, but both models remain similar regardless of
velocity.
0
5000
10000
15000
20000
25000
30000
35000
40000
45000
0 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.0035 0.004 0.0045 0.005
LD
v
Brownian
Waypoint
Figure 4: Link duration (LD) for the Brownian and RWP
mobility models with respect to velocity for N = 10
3
, ρ =
1.3. At low velocities the Brownian model has a signifi-
cantly larger duration, but both mobility models converge
as velocity increases.
previous work (Meloni et al., 2009), which requires
L = 27.735 for 10
3
nodes.
LCR =
∑
i∈A
∑
T
t
E
i
A
(t) + E
i
R
(t)
|A| × T
(2)
LD =
∑
i∈A
∑
T
t
∑
e∈E
i
R
(t)
D(e)
E
T
(3)
In Figure 3 we compare the LCR for the Brownian
and RWP mobility models with respect to velocity.
RWP exhibits a slightly higher LCR than the Brow-
nian mobility in all cases, but they do not show any
indication of divergence up to v = 0.02. This indi-
cates that the RWP mobility model is not introducing
additional volatility with respect to the addition and
removal of edges.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
62
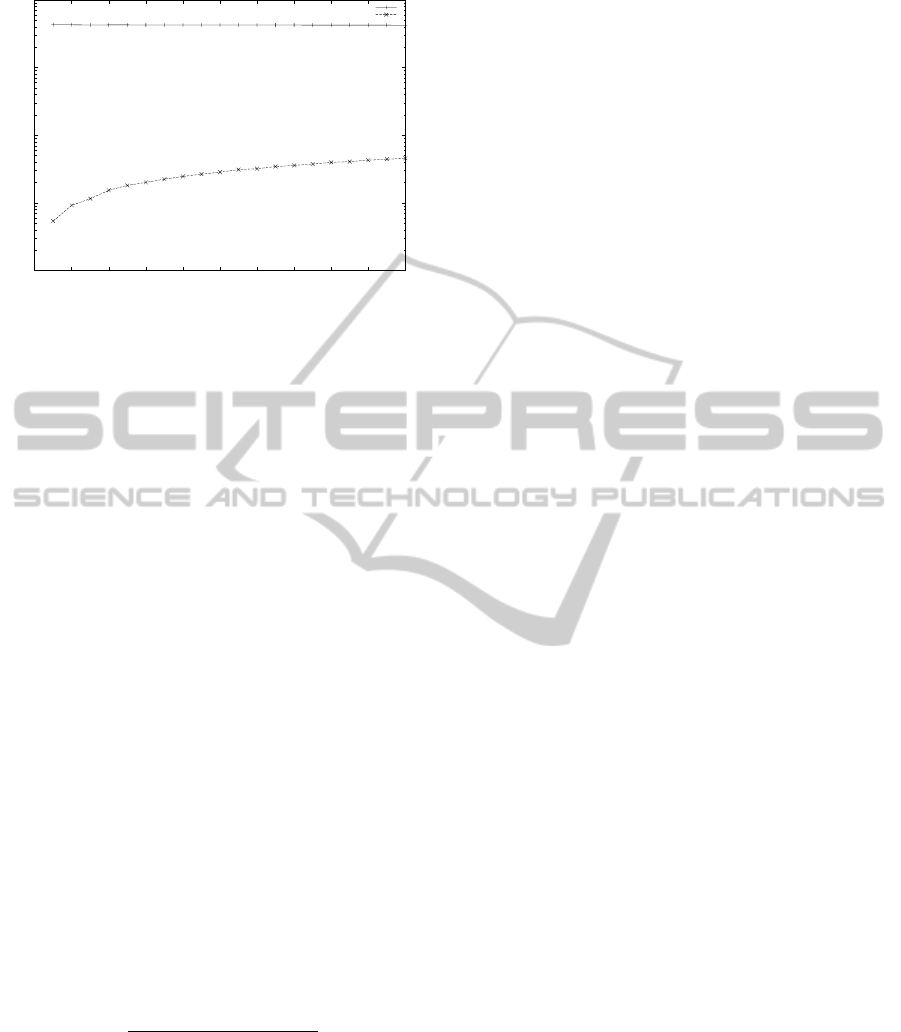
0.0001
0.001
0.01
0.1
1
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
LR
v
Brownian
Waypoint
Figure 5: Link repetition (LR) for the Brownian and RWP
mobility models with respect to velocity for N = 10
3
, ρ =
1.3. The Brownian model has relatively fixed LR regardless
of velocity while RWP has a vastly different LR value that
changes with respect to velocity.
In Figure 4 we show the LD for Brownian and
RWP mobility with respect to velocity. At very low
velocities these models exhibit significantly differ-
ent link durations, with Brownian motion maintain-
ing links orders of magnitude longer than RWP at
v = 0.005. However, as the velocity increases both
mobility models converge to similar link durations.
Because the Brownian mobility randomly chooses a
new direction at each time step there is an increased
likelihood of remaining in range of a neighbor until
the random walk leads the agent away. On the other
hand, because RWP uses time-dependent movement,
an agent within range that moves away in a given time
step is likely to continue on that path.
Intuitively, these mobility models should differ
significantly with respect to the diversity of the edges
that are formed. Two arbitrary nodes in the Brown-
ian mobility model are more likely reform the same
edge within a short period of time than the same pair
of nodes in the RWP mobility model. To capture this
behavior we define the link repetition (LR) of a dy-
namic graph in Equation 4, with L(e) being the last
time step that edge e existed and E
A
being the set of
all edges added over all time steps.
LR =
∑
T
t
∑
e∈E
A
(t)
(t − L(e))
−1
|A| × |E
A
|
(4)
This metric measures the likelihood of newly
formed edges being between vertices that were re-
cently connected. By accumulating the inverse of the
time between link disconnect and reconnection we
can identify conditions under which neighbors are in-
teracting with the same neighbors, regardless of link
change rate. A high LR value indicates that agents
are reforming edges with neighbors within a relatively
short period of time after the edge is removed. A low
value indicates that agents are interacting with a wide
range of other agents and not often reforming edges
with the same neighbors.
In Figure 5 we show the LR value for both mo-
bility models. Brownian motion maintains a fixed
link repetition (LR ≈ .43) value regardless of veloc-
ity, while the RWP mobility has an LR value that is
consistently much smaller and increases with respect
to velocity. These values reflect the stepwise random
behavior of Brownian motion that leads to edge re-
connection at a fixed rate, while the time-dependent
behavior of RWP mobility leads to a low reconnection
rate. As velocity increases, the RWP mobility moves
agents at a faster rate, leading to more opportunities
for reconnection as they cover more of the space in
less time.
While link retention is not the singular measure
to differentiate between Brownian and RWP mo-
bility, it does provide some insight into why these
models should behave differently with respect to the
emergence of cooperation. Clusters of cooperators
thrive on repeated interaction with other cooperators
(Oliphant, 1994), so repeated interaction (even with
a small number of time steps disconnected) can be a
powerful influencer of the convergence to cooperation
in the whole population . When repeated interaction is
limited, the pockets of cooperation are no longer char-
acterized primarily by the agents that are members of
the clusters, but rather the inherent structure of these
clusters. In the RWP mobility model the clusters of
cooperation must be stabilized by reduced movement
to allow cooperation to stabilize and convert the con-
stant stream of new agents to cooperation.
5.1 Node Density
In Figure 6 we show the effect of density on how
often the population converges to full cooperation.
These results are very similar to those found in (Mel-
oni et al., 2009), shown in Figure 7 but are at a ve-
locity of v = 0.001 rather than v = 0.01, an order of
magnitude reduction. Simulations run at v = 0.01 us-
ing RWP movement always converged to defection,
regardless of density. This significant difference fur-
ther reinforces that RWP mobility has a strong effect
on the stability of cooperative ’communities’ that can
be remedied by decreasing the relative velocity of the
agents.
As show in Figure 6, at low values of density
(ρ . 1) the agents are sparsely distributed and co-
operators are unable to form regions of cooperation.
Conversely, at high densities (ρ & 7) agents are well-
mixed and interact with a large number of other
EvolutionofCooperationinPacketForwardingwiththeRandomWaypointModel
63
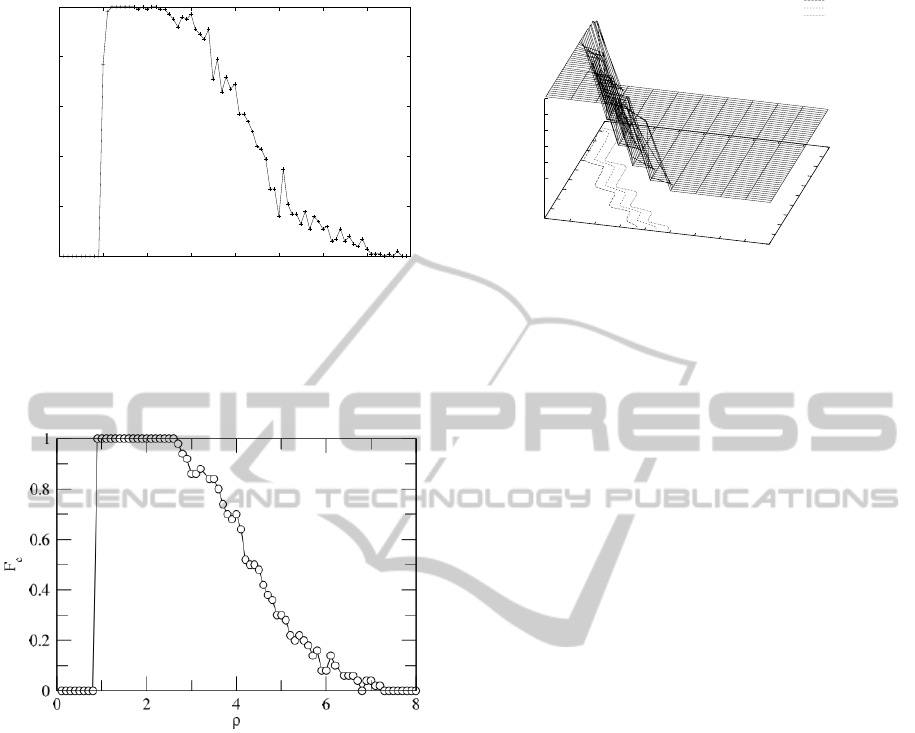
0
0.2
0.4
0.6
0.8
1
0 1 2 3 4 5 6 7 8
F
C
l
Figure 6: Fraction of simulations F
C
using Random Way-
point mobility that converge to full cooperation as a func-
tion of density ρ with fixed value of N = 10
3
, b = 1.1, and
v = 0.001. Results are given as a fraction of 100 simulation
runs.
Figure 7: Fraction of simulations F
C
using Brownian mo-
bility that converge to full cooperation using Brownian mo-
bility as a function of density ρ with fixed value of N = 10
3
,
b = 1.1, and v = 0.01, as reported in (Meloni et al., 2009).
Results are given as a fraction of 100 simulation runs.
agents. In this case there are many opportunities for
defectors to get a high payout and encourage coop-
erators to defect. Finally, there is a region of den-
sity (1.2 . ρ . 2.4) where the population will al-
most always converge to cooperation and we observe
a steady decrease in convergence to cooperation as ρ
approaches 7.
5.2 Velocity vs. Benefit of Defection
We now seek to determine the parameter values that
encourage cooperation in mobile ad hoc network
packet forwarding. Due to the complexity and over-
lap of the models of interaction and mobility, a purely
analytical solution to this problem is difficult to de-
rive. Therefore, we seek an empirical solution based
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0
0.2
0.4
0.6
0.8
1
F
C
0.9
0.5
0.1
b
v
F
C
Figure 8: Fraction of simulations F
C
out of 100 that con-
verge to cooperation with respect to velocity (v) and the
temptation to defect (b) with fixed values of N = 10
3
and
ρ = 1.3.
on modeling and simulation of a set of random in-
stances. Of particular interest are the effects of node
density on cooperation and the relationship between
velocity and the benefit of defection. Because r is
fixed at r = 1, to adjust the density we must change
the size of the L × L space. This will alter the set
of possible agents chosen as neighbors while keeping
the velocity relative to the fixed communication ra-
dius. Agents play a pure strategy and are initialized
with a random strategy with 50% probability of being
a cooperator or defector.
In order to show a wide range of behavior we
have run simulations for different values of velocity
and temptation to defect. In Figure 8 the effects of
these parameters on the convergence to cooperation
is shown. For very small values of b cooperation is
more likely, even as the velocity is increased. This
can be attributed to the relatively low payoffs that
selfish agents will receive, reducing the likelihood of
neighbor nodes choosing to adopt the same strategy.
Likewise, an increase in velocity also diminishes the
chances of the simulation converging to cooperation.
As clusters of cooperators form, the agents rely on
their neighborhood to boost their own payoffs as well
as help to influence other agents to also engage in
cooperation. Additionally, it’s important that agents
moving through the region of cooperation have am-
ple opportunity to observe the benefits and adopt the
strategy before they move out of the cluster. As ve-
locity increase there is a corresponding increase in
the frequency and number of intruding defectors that
can exploit cooperators for higher payoffs and pro-
vide neighboring agents with incentive to also defect.
Additionally, an increased velocity reduces the time
that and agent passing through the cluster will have to
interact with cooperators and adopt their strategy for
itself. These challenges, while not unique to the RWP
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
64

mobility model, are significantly more pronounced in
their effects.
6 DISCUSSION
We show that more realistic mobility models, as op-
posed to fully random models, can make it more diffi-
cult for cooperation to evolve in a population of indi-
viduals. We also provide a set of assumptions that be-
gin to bridge the gap between theoretical agent inter-
action models and distributed packet forwarding us-
ing local decision processes. The main contribution
of this work is to show that the random waypoint mo-
bility model, a more realistic representation of agent
movement for mobile ad hoc networks, has a signifi-
cant effect on the emergence of cooperation.
Full convergence to cooperation was realized in
the RWP model, but only by significantly reducing
the velocity of the agents to counteract the resulting
volatility due to a lack a stability in cooperation clus-
ters. Unlike random walk models, where agents are
likely to remain near each other for many time steps,
the RWP model define vectors of movement that will
often result in agents following divergent paths. In the
Brownian mobility model, regions of cooperation are
composed of a community of agents that are likely
to remain together. The RWP model, on the other
hand, yields cooperation regions in which the mem-
ber agents are fleeting and the stability is influenced
by the interaction structure and its ability to convert
defectors to cooperators as they enter the region.
These results can be used to design internal mech-
anisms for individual networked devices as well as
provide insight into the effect of mobility on collec-
tions of ad hoc networked devices. Significant work
is still needed to show the applications of these results
to real networks, but they provide a foundation to sup-
port the applicability of evolutionary game theory to
the design and analysis of mobile ad hoc networks.
6.1 Future Work
There is a wealth of movement models, surveyed in
(Bai and Helmy, 2004), that are intended to model
specific real-world phenomenon. Temporal depen-
dency models generate motion that is dependent on
prior time steps and model gradual turning and ac-
celeration. Spatial dependency models provide mech-
anisms for squad-based movement that would more
accurately model devices being carried by groups of
people. Geographic restriction models consider envi-
ronments where movement and communication is re-
stricted by the existence of impassable objects, such
as buildings. Each of these models and their unions
have unique properties that will no doubt have an ef-
fect on the evolution of cooperation.
We plan to explore other types of games that cap-
ture ad hoc network behavior, such as those discussed
in (Kamhoua et al., 2010). The pure strategies used
in our simulations assumes that an agent does not
discern between the identities of neighboring nodes.
While this provides an efficient, memoryless oper-
ating methodology, there is the potential to include
identification of neighbors and recall of historical in-
teractions. This additional bookkeeping would allow
for iterated play and, as a result, more sophisticated
strategies such as Tit for Tat or Grim Trigger (Axel-
rod, 2000).
The replicator dynamics used for adopting the
strategy of a neighbor relies on the communication of
reward or the ability to observe the action and payoff
that neighboring agents receive. While this is a com-
mon mechanism for evolutionary games it not a real-
istic assumption in physical environments with selfish
agents that see no benefit in making this information
available. In these cases a new method for updating
an agent’s strategy will be necessary.
ACKNOWLEDGEMENTS
We would like thank Charles Kamhoua for offering
his expertise, invaluable guidance and thorough re-
view of our work.
REFERENCES
Assenza, S. (2008). Enhancement of cooperation in highly
clustered scale-free networks. In Physical Review E.
Axelrod, R. (1992). The evolution of cooperation. Science.
Axelrod, R. (2000). On six advances in cooperation theory.
Analyse & Kritik, 22(1):130–151.
Bai, F. and Helmy, A. (2004). A survey of mobility mod-
els. Wireless Adhoc Networks. University of Southern
California, USA, 206:1–30.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and
Hwang, D. (2006). Complex networks: Structure and
dynamics. Physics Reports, 424(4-5):175–308.
Cho, S. and Hayes, J. (2005). Impact of mobility on connec-
tion in ad hoc networks. In Wireless Communications
and Networking Conference, 2005 IEEE, volume 3,
pages 1650–1656. IEEE.
Cohen, M., Riolo, R., and Axelrod, R. (1999). The
emergence of social organization in the prisoner’s
dilemma: How context-preservation and other factors
promote cooperation. Working Papers.
Helbing, D. and Yu, W. (2009). The outbreak of cooper-
ation among success-driven individuals under noisy
EvolutionofCooperationinPacketForwardingwiththeRandomWaypointModel
65

conditions. In Proceedings of the National Academy
of Sciences, volume 106, page 3680. National Acad
Sciences.
Ho, C., Obraczka, K., Tsudik, G., and Viswanath, K.
(1999). Flooding for reliable multicast in multi-hop
ad hoc networks. In Proceedings of the 3rd interna-
tional workshop on Discrete algorithms and methods
for mobile computing and communications, pages 64–
71. ACM.
Johnson, D. and Maltz, D. (1996). Dynamic source routing
in ad hoc wireless networks. pages 153–181. Springer.
Kamhoua, C., Pissinou, N., Miller, J., and Makki, S. (2010).
Mitigating routing misbehavior in multi-hop networks
using evolutionary game theory. In IEEE Globecom
workshop on advances in communications and net-
works.
Kendall, G., Yao, X., and Chong, S. (2007). The iterated
prisoners’ dilemma: 20 years on, volume 4. World
Scientific Pub Co Inc.
Luke, S., Cioffi-Revilla, C., Panait, L., Sullivan, K., and
Balan, G. (2005). Mason: A multi-agent simulation
environment. In Simulation: Transactions of the so-
ciety for Modeling and Simulation International, vol-
ume 82(7), pages 517–527.
Marti, S., Giuli, T., Lai, K., and Baker, M. (2000). Mitigat-
ing routing misbehavior in mobile ad hoc networks.
In Proceedings of the 6th annual international confer-
ence on Mobil computing and networking, pages 255–
265.
Meloni, S., Buscarino, A., Fortuna, L., and Frasca, M.
(2009). Effects of mobility in a population of pris-
oner’s dilemma players. Physical Review E, pages 1–
4.
Nisan, N. (2007). Algorithmic Game Theory. Cambridge
University Press, Cambridge.
Nowak, M. (1992). Evolutionary games and spatial chaos.
Nature.
Oliphant, M. (1994). Evolving cooperation in the non-
iterated prisoner’s dilemma: The importance of spatial
organization. In Proceedings of the fourth artificial
life workshop, Cambridge, MA, pages 349—-352.
Penrose, M. (2003). Random geometric graphs, volume 5.
Oxford University Press, Oxford.
Perc, M. and Szolnoki, A. (2008). Social diversity and
promotion of cooperation in the spatial prisoners
dilemma game. Physical Review E, 77(1):011904.
Poncela, J., G
´
omez-Garde
˜
nes, J., Flor
´
ıa, L., S
´
anchez, A.,
and Moreno, Y. (2008). Complex cooperative net-
works from evolutionary preferential attachment. vol-
ume 3, page e2449. Public Library of Science.
Poncela, J., G
´
omez-Garde
˜
nes, J., Traulsen, A., and Moreno,
Y. (2009). Evolutionary game dynamics in a growing
structured population. New Journal of Physics, 11.
Szolnoki, A., Perc, M., and Danku, Z. (2008). Making
new connections towards cooperation in the prisoner’s
dilemma game. EPL (Europhysics Letters), 84:50007.
Tanachaiwiwat, S., Dave, P., Bhindwale, R., and Helmy,
A. (2004). Location-centric isolation of misbehav-
ior and trust routing in energy-constrained sensor net-
works. In 2004 IEEE international conference on per-
formance, computing, and communications.
Viennot, L., Jacquet, P., and Clausen, T. (2004). Analyzing
control traffic overhead versus mobility and data traf-
fic activity in mobile ad-hoc network protocols. Wire-
less Networks, 10(4):447–455.
Weibull, J. (1997). Evolutionary game theory. The MIT
press.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
66
