Using Path Planning Techniques to Improve Airway Tree Segmentation
from CT Images
Paolo Cabras and Jan Rosell
Institute of Industrial and Control Engineering, Universitat Polit
`
ecnica de Catalunya, Barcelona, Spain
Keywords:
Airway Segmentation, Path Planning, Bronchi Connection.
Abstract:
Virtual Bronchoscopy (VB) permits the preplanning of operations concerning the airways and provides the
necessary guidance to reach the pulmonary lesions. Fundamental for a good VB is the reconstruction of a 3D
model of the airways from the CT images. Airway segmentation algorithms usually return the biggest detected
volume connected to the trachea (the root tree), but many of them also reconstruct during the segmentation
process, small parts not connected to the root tree. To overcome this problem this paper proposes a method,
based on path planning techniques, that is able to connect the small isolated pieces of bronchi to the terminal
points of the root airway tree, taking into account the growing direction of the branches and the gray values of
the CT images. As a result, a more complete 3D model of the airways is obtained.
1 INTRODUCTION
Bronchoscopy is an interventional medical procedure
used to analyze the tracheobronchial tree, mainly to
obtain samples from a specific lung site identified
by chest X-ray computed tomography (CT). Virtual
Bronchoscopy (VB) is a computer-generated 3D
reconstruction that allows physicians to interactively
explore the tracheobronchial tree model. VB can
make lymph nodes visible by showing the virtual
bronchial tubes semitransparent, or can automatically
plan a path from the trachea to peripheral lung
lesion (Ferguson and McLennan, 2005; Rosell
et al., 2012). Recent clinical studies have proved
that VB navigation system can effectively shorten
the examination and operation time (Shinagawa
et al., 2007). Real bronchoscopy aids have also
been proposed to guide the execution of the real
bronchoscopy using augmented reality techniques,
i.e. by superimposing the computed path over
the image fed back by the camera, which results
in an increase in the success rate to reach the
lesion (Eberhardt et al., 2010).
1.1 Motivation
A vital task for the VB is the segmentation of the
airway tree from CT slices. This is a difficult task,
specially for the the thinnest bronchi, due to image
reconstruction artifacts, patient movements or disease
and the partial volume effect. Different segmentation
methods have been proposed, that can be divided into
three categories (Fetita et al., 2004):
a) 2D/3D Techniques: The aim of these
techniques is to detect the potential airway regions on
2D axial images and then select the right candidates
to reconstruct the 3D model. For instance, (Fetita
and Preteux, 1999) use mathematical morphology
operations (binary and gray-scale reconstruction)
to find the candidates in 2D slices and then the
reconstruction of the airway is performed using a
3D propagation driven by 3D topological structure.
Usually, the 2D segmentation techniques used may
present some difficulties with the smallest bronchi
and the obtention of an entirely connected structure
may not be possible (if the algorithm fails to detect a
candidate bronchus in a single slice then this bronchus
is interrupted, preventing the reconstruction from
being complete).
b) 3D Region Growing Techniques: Starting with
a seed located at the trachea, region growing methods
determine the airway region using thresholds (Pinho
et al., 2009). The reconstruction accuracy in the
region-growing based method depends directly on
the threshold settings. Given the great difference
in the gray values between biggest and smallest
bronchi, a global threshold does not allow to detect
and reconstruct a big volume. Better results can be
achieved with a dynamic threshold, but also in this
case if severe stenosis or local occlusions (due to
189
Cabras P. and Rosell J..
Using Path Planning Techniques to Improve Airway Tree Segmentation from CT Images.
DOI: 10.5220/0004237101890195
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 189-195
ISBN: 978-989-8565-36-5
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

noise or pathologies) occur, the growth is blocked
and the algorithm fails to detect the distal bronchi
due to these interruptions. Consequently, although an
algorithm would detect pieces of distal small bronchi,
it could happen that these pieces are not considered
in the final result since they are not connected to the
main tracheobronchial tree.
c) Hybrid Methods: Hybrid methods combine
the previous approaches. For instance, (Sonka
et al., 1996) propose a rule-based method consisting
in a combination of 3D seeded region growing to
identify large airways, rule-based 2D segmentation
of individual CT slices to identify probable locations
of smaller diameter airways, and the merging of
airway regions across the 3D set of slices. The
output is often a non-connected region, i.e. the
main tracheobronchial region plus isolated regions
segmented as airways but disconnected from it.
To overcome the problem of the isolated
segmented regions that appear in any of the above
techniques, some algorithms include a final 3D
connection step. For instance, in (Bauer et al.,
2009b) tubular structures are detected in the data
volume and then the different structures are connected
together according to branching angle, branch radius
and distance. Similarly, (Graham et al., 2010)
connects the disjoint branches interpolating their
cross sectional surfaces, trying to minimize a
connection cost based on the directions of the
branches and the gray values of the voxels
Similar disconnection problems appear in digital
reconstruction of 3D neuron structures, due to the low
single-to-noise ratio of the 3D microscopic images.
To solve this problem (Peng et al., 2010) proposed a
shortest path graph algorithm that uses both metrics
of Euclidean length and of image voxel intensity. In
this line, the motivation of the present paper is to
contribute to the airway tree segmentation problem
with the proposal of a simple yet powerful method
based on path planning techniques.
1.2 Path Planning
Path planning is a mature discipline in robotics.
The basic path planning problem is focused in the
computation of collision free paths for a robot from
an initial to a final configuration. This planning
is usually done in the robot configuration space
(which is a space with dimensionality equal to
the degrees of freedom of the robot), where the
problem is reduced to the planning of a path of a
point (representing the robot) among (accordingly
enlarged) obstacles. One of the most used techniques
for low dimensional problems is based on the
(a) (b)
Figure 1: Paths on a 2D space from an initial cell at the
bottom-right corner to the goal cell at the top-left one,
computed with the NF1 function (a) and with the NF1
function modulated by the clearance (b).
(a) (b)
Figure 2: (a) The root tree reconstructed using a region
growing method with adaptive threshold; (b) the root tree
and the other isolated parts segmented as airways (in
purple).
computation of a potential field on a grid representing
the discretized configuration space, with a global
minima at the goal configuration. The planning is
then reduced to the following of the negated gradient
of the potential field.
Potential fields can be computed using navigation
functions, that are local minima-free potential
functions computed over a grid. The navigation
function NF1 (Latombe, 1991) is obtained by
computing the L1 distances from a cell of the grid
(the goal) by a wavefront propagation (Fig. 1a).
The problem of the paths obtained with the NF1
navigation function is that they may graze the
obstacles, but the potential field provided by a
navigation function can be modulated by varying
the values being propagated, e.g. by decreasing the
potential being propagated by a value proportional to
the clearance (Rosell et al., 2012) (Fig. 1b).
1.3 Proposal Overview
A stack of CT images of a chest is a 3D grid of
voxels with different gray-level values (the darker
corresponding to the airways), and the airway
segmentation algorithms label these voxels as interior
or exterior. All those voxels labeled as interior
and connected to the trachea conform the root tree
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
190

(Fig. 2a). Other isolated sets of voxels labeled
as interior but not connected to the root tree
may represent parts of interrupted bronchi or badly
segmented regions (purple regions in Fig. 2b).
The proposal of the present paper is the use of
path planning techniques based on modulations of the
navigation function NF1, to connect the set of voxels
of an isolated region segmented as airway to the root
tree. The proposal is structured in two steps:
1. Determination of the Interrupted Branches: the
point where the root tree is interrupted and the
direction of the interrupted bronchus are to be
determined.
2. Connection Process: the interrupted branch has to
be connected to a candidate isolated region among
all the isolated regions around a neighborhood of
the interrupted branch point.
Different modulations of the navigation function NF1
will be used in each step.
2 PROPOSED METHOD
This section describes the two steps of the proposal.
Although the procedure is done in the 3D grid, for
a better comprehension of the whole process, the
different steps of the algorithm are illustrated in 2D
using the single slice shown in Fig. 3, corresponding
to a transversal plane of a stack of CT images. In
this figure, a bronchus that evolves horizontally on the
slice is shown interrupted: the regions shown in green
correspond to regions segmented as airways that are
connected to the root tree, the regions shown in red
correspond to regions also segmented as airways but
disconnected from the root tree (the one on the right
is a badly segmented region whereas the other ones
correspond to pieces of bronchi).
2.1 Interruption Point and Direction
The root tree has been computed using a region
growing procedure with an adaptive threshold. Then,
the points where the root tree is interrupted, i.e. the
interruption points, are determined computing the
basic NF1 function on the root tree, i.e. propagating
a wavefront from the beginning of the trachea and
looking for the local maxima of the navigation
function. In the 2D example, there is one interruption
point, called g, shown in orange in Fig 3b.
The direction of the bronchus at the interruption
point is computed using a modulation of the
navigation function NF1, called regressive NF1. The
procedure works as follows:
(a)
g
(b)
Figure 3: (a) CT slice with a bronchus to be segmented; (b)
the result of segmentation: green regions are connected to
the root tree, red regions are disconnected. The orange point
represent the interruption point g.
• A high value is assigned to the interruption point
g = (x
g
,y
g
,z
g
) (orange pixel in Fig. 4).
• The potential of each voxel is propagated to its
airway neighbors. The value propagated depends
on the distance to the walls. Let d
j
be the potential
of a given voxel j, d
i
that of the neighbor voxel i
being expanded, c
j
be the clearance of node j
(i.e. the L1 distance to the non-airway voxels),
and C
max
the maximum clearance. Then:
d
j
=
{
d
i
− 1 +
C
max
−c
j
C
max
if
C
max
−c
j
C
max
< 0.9
d
i
− 0.1 otherwise
(1)
• Starting at the interruption point, a gradient
descent is followed for a given number of
steps (currently fixed to five). The reached
voxel is labeled as point o = (x
o
,y
o
,z
o
), and
the interruption direction is v
o
= (x
g
,y
g
,z
g
) −
(x
o
,y
o
,z
o
) (red arrow in Fig. 4).
Fig. 4 is a representation of the regression NF1
function computed on the example of Fig. 3. This
method permits to easily calculate the direction of a
branch without knowing the skeleton of the root tree.
2.2 Connection Process
The connection process is done by defining a
modulation of the navigation function NF1,
called connection NF1, on a neighborhood of
the interruption point g (this neighborhood is a
box centered at g and with 21 voxels per axis).
Considering point g as the potential minima, the
potential landscape will be modulated to consider:
• The distance to g (the potential of a voxel p
j
will
be proportional to the L1 distance from g to p
j
).
UsingPathPlanningTechniquestoImproveAirwayTreeSegmentationfromCTImages
191

Figure 4: The regression NF1 function computed on the
particular of Fig. 3(b). Warm colors represent highest
potential values, cool colors the lowest. Following the
negated gradient the origin of the direction vector v
o
is
determined.
o
g
v
o
v
j
θ
p
j
Figure 5: Angle θ between the direction v
o
of the
interrupted branch, and the direction v
j
defined by the
interruption point g and the current analyzed voxel p
j
.
• The directionality (the potential will increase
slower in the directions around that defined by the
interruption vector v
o
).
• The gray level of the voxels (the potential will
increase slower along darker voxels, i.e. those
with a higher probability of pertaining to the
interior of the airways).
The procedure to compute the connection NF1 starts
assigning a zero value to the interruption point g.
Then, the potential is iteratively propagated (within
the neighborhood box) as follows:
d
j
= d
i
+ (1 − k
G
− k
θ
) (2)
where:
• k
G
depends on the gray level of the considered
voxel and on wether the segmentation algorithm
has labeled it as airway or not. If S is the set of all
the voxels segmented as airways, then:
k
G
=
{
0.98 if p
j
∈ S
min{0.98,t
HU
e
−
1
2
(
t
HU
−1
σ
HU
)
2
} if p
j
/∈ S
(3)
where t
HU
is the ratio between the gray level of
the voxel and the minimum gray value of the data
set
1
.
• k
θ
is related to the angle θ between the
interruption direction (v
o
) and the vector from
point g to the considered voxel p
j
, i.e. v
j
=
(x
j
,y
j
,z
j
) − (x
g
,y
g
,z
g
) (Fig. 5):
k
θ
=
{
−1 if cos(θ) < 0
cos(θ)e
−
1
2
(
θ
σ
θ
)
2
otherwise
(4)
As it can be appreciated, both the gray and
orientation terms are modulated by a Gaussian curve
which is centered at the minimum gray level of the
data set (which correspond to t
HU
= 1) for k
G
, and
at 0 rad for k
θ
. The value of the respective sigmas
regulate the width of the “bell curve”. Concerning
the direction, (Graham et al., 2010) and (Bauer et al.,
2009a) consider that the maximum branching angle
for the airway tree is π/3 rad, and connect only
those branches that subtend angles smaller than this
value. The proposed modulation of the NF1 function
includes such a discrimination, by setting σ
θ
= π/6,
i.e. to have a heat attenuation of k
θ
in those voxels
whose direction is greater than π/3 rad. On the other
hand, all the regions that have a gray value greater
than −700 HU are probably not airway lumen voxels,
that is why (considering the minimum value equal to
−1000 HU) σ =
−700
−1000
= 0.7 is set for the Gaussian
function of k
G
.
Starting at g, the navigation function just defined
is computed in all the considered box. With the
scenario of Fig. 3 the resulting potential is shown in
Fig. 6.
Once the connection NF1 values are computed,
the connection between the root tree and the isolated
branches is done with the following steps:
• For each isolated region within the neighbor box,
select the point with lowest potential (points e
1
, e
2
and e
3
in Fig. 7a).
• Among the selected points choose the one with
lowest potential value (points e
1
in Fig. 7a).
1
HU stands for Hounsfield Units, that is the scale that
measures the radiodensity. The darker voxels correspond to
the air, that has a value of -1000HU.
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
192

Figure 6: 3D representation of the connection NF1
computed on the 2D scenario of Fig. 3(a).
e
1
e
2
e
3
(a) (b)
Figure 7: In (a) the interruption point g is shown in orange,
the isolated region closest points are shown in cyan. In
(b) the connection result is shown (the isolated regions that
where bronchi have been correctly connected and the one
on the right that was a false positive is not).
• From that point follow the negated gradient of
the potential function until the point g with zero
potential is reached.
• Label all the voxels of the previous step as airway.
Repeating the whole procedure again, the second
isolated region is also connected. It can be
appreciated that, thanks to the directionality
discriminant, the chosen navigation function avoids
the connection with the false positive region on the
right labeled as airway lumen by the segmentation
algorithm. Fig. 7b shows the final reconstructed
bronchus.
3 RESULTS
This section shows some results using the complete
3D stack of CT images that validate the proposed
approach. The regressive NF1 has been able to
correctly capture the centerline of the interrupted
Figure 8: 3D example of the interruption points and the
associated neighborhood boxes where the isolated branches
to be connected may lie. The root tree is shown in blue, the
isolated branches in gold.
bronchi without the need to know the entire skeleton
of the airway tree; the connection NF1 function has
been able to correctly connect the interrupted point
to the correct isolated region, avoiding those false
positive regions very near to the interruption point but
outside the branch orientation cone or separated from
the branch by a vessel or a clear region.
Fig 8 shows an example of the interruption points
and of the associated neighborhood boxes where the
connection NF1 is computed to find the connection
with the isolated branches that lie within.
Fig. 9 shows in rows two examples of the
connection results. The airway tree reconstructed
with region growing technique (in gold) and the
branches or pieces of branches detected by the
segmentation procedure (in purple) are shown on the
left; the connection between the root tree and the
separated branches is shown in the middle, and the
final result is shown on the right.
The current implementation is done using the
Amira software and its connection with Matlab. The
computational cost is high (it lasts an average of 50
minutes for a whole CT stack) but the qualitative
results are very significative since the resulting airway
tree can be extended with many already segmented
branches that would otherwise be lost.
4 CONCLUSIONS
In the field of airway tree segmentation from CT
images, there are many algorithms that return just
the root tree even though in previous steps they are
able to detect other airway lumen regions which are
not present in the final result just because they are
not connected to the root tree. With this in mind,
this paper has presented a novel approach based on
path planning techniques to connect the root tree to
UsingPathPlanningTechniquestoImproveAirwayTreeSegmentationfromCTImages
193

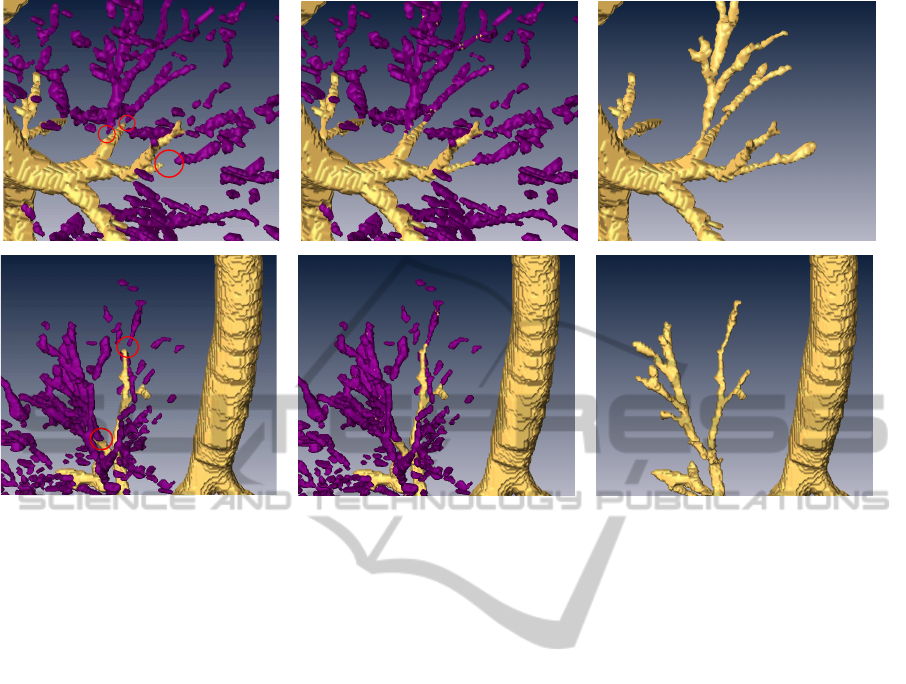
Figure 9: Two examples (in rows) of the 3D connection process. The gold colored region on the left figures is the root tree
and the purple volumes are the isolated branches, the parts to be connected are encircled in red. The middle figures show the
connection result and the right figures the final airway tree.
those isolated regions that possibly represents a piece
of a bronchus. Two local minima-free navigation
function have been created to this end, first, to
individuate the branch ending direction and, then, to
find a path to connect the disconnected branches. The
proposal takes as input the result of the segmentation
algorithms and return a better airway tree model in
terms of completeness, since it can connect the airway
root tree to the other isolated detected branches
according to the gray level of the regions in the
original CT scan and to morphological considerations
(orientation and proximity).
Current work includes the implementation of a
shape filter to eliminate those disconnected regions
that do not appear to be bronchial branches and that
are not aligned with the interrupted branch. This
will accelerate the computation time of the connection
process. Also, a more exhaustive computational
evaluation and comparison with other alternatives is
under development.
REFERENCES
Bauer, C., Bischof, H., and Beichel, R. (2009a).
Segmentation of airways based on gradient vector
flow. In Second International Workshop on
Pulmonary Image Analysis, pages 191–200. MICCAI.
Bauer, C., Pock, T., Bischof, H., and Beichel, R. (2009b).
Airway tree reconstruction based on tube detection. In
Second International Workshop on Pulmonary Image
Analysis, pages 203–213. MICCAI.
Eberhardt, R., Kahn, N., Gompelmann, D., Schumann, M.,
Heussel, C. P., and Herth, F. J. F. (2010). Lungpoint-a
new approach to peripheral lesions. Journal of
Thoracic Oncology, 5(10):1559–1563.
Ferguson, J. and McLennan, G. (2005). Virtual
bronchoscopy. Proceedings of American Thoracic
Society, 2:488–491.
Fetita, C. and Preteux, F. (1999). Three-dimensional
reconstruction of human bronchial tree in hrct. In
Proc. of SPIE, volume 3646, pages 281–294.
Fetita, C. I., Pr
ˆ
eteux, F., Beigelman-Aubry, C., and Grenier,
P. (2004). Pulmonary airways: 3-d reconstruction
from multislice ct and clinical investigation. IEEE
Transatcions on medical imaging, 23(11):145–152.
Graham, M. W., Gibbs, J. D., Cornish, D. C., and Higgins,
W. E. (2010). Robust 3-d airway tree segmentation
for image-guided peripheral bronchoscopy. In IEEE
transactions on Medical Imaging, volume 29, pages
982–97. IEEE.
Latombe, J.-C. (1991). Robot Motion Planning. Kluwer
Academic.
Peng, H., Ruan, Z., Atasoy, D., and Sternson, S.
(2010). Automatic reconstruction of 3d neuron
structures using a graph-augmented deformable
model. Bioinformatics, 26:i38–i46.
Pinho, R., Luyckx, R., and Sijbers, J. (2009). Robust region
growing based intrathoracic airway tree segmentation.
BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
194

Second International Workshop on Pulmonary Image
Analysis, pages 261–277.
Rosell, J., Perez, A., Cabras, P., and Rosell, A. (2012).
Motion planning for the virtual bronchoscopy. In
IEEE International Conference on Robotics and
Automation, pages 2932 – 2937. IEEE.
Shinagawa, N., Yamazaki, K., Onodera, Y., Asano, F.,
Ishida, T., Moriya, H., and Nishimura, M. (2007).
Virtual bronchoscopy navigation system shortens
the examination time: Feasibility study of vrtual
bronchoscopy navigation system. Lung Cancer,
56(2):201–206.
Sonka, M., Park, W., and Hoffman, E. A. (1996).
Rule-based detection of intrathoracic airway trees. In
IEEE transactions on Medical Imaging, volume 15,
pages 314–326. IEEE.
UsingPathPlanningTechniquestoImproveAirwayTreeSegmentationfromCTImages
195