Inverse of Lorentzian Mixture for Simultaneous Training of Prototypes

and Weights

Atsushi Sato and Masato Ishii

Information and Media Processing Laboratories, NEC Corporation 1753,

Shimonumabe, Nakahara-ku, Kawasaki, Japan

Keywords:

Lorentzian Mixture, Nearest Neighbor, Loss Minimization, Bayes Decision Theory, Machine Learning.

Abstract:

This paper presents a novel distance-based classiﬁer based on the multiplicative inverse of Lorentzian mix-

ture, which can be regarded as a natural extension of the conventional nearest neighbor rule. We show that

prototypes and weights can be trained simultaneously by General Loss Minimization, which is a generalized

version of supervised learning framework used in Generalized Learning Vector Quantization. Experimental

results for UCI machine learning repository reveal that the proposed method achieves almost the same as

or higher classiﬁcation accuracy than Support Vector Machine with a much fewer prototypes than support

vectors.

1 INTRODUCTION

Distance-based classiﬁers have been widely used in

real applications, because they achieve good perfor-

mance in spite of their simple structures with a few

prototypes. One popular learning algorithm of pro-

totypes is Learning Vector Quantization (LVQ) (Ko-

honen, 1995), and the margin-based theoretical anal-

ysis has proved that LVQ is a family of large mar-

gin classiﬁers (Crammer et al., 2003). In the early

stage of LVQ research, learning algorithms were im-

proved by heuristic approaches. However, improve-

ments have been conducted based on loss minimiza-

tion, since Generalized Learning Vector Quantization

(GLVQ) (Sato and Yamada, 1996; Sato, 1998) was

proposed. One of the major improvements concerns

the choice of an appropriate distance measure (Ham-

mer and Villmann, 2002; Schneider et al., 2009; Vill-

mann and Haase, 2011).

Meanwhile, kernel classiﬁers have been investi-

gated, and Support Vector Machine (SVM) (Cortes

and Vapnik, 1995) has become one of the powerful

classiﬁcation method. Many works have shown that

SVM outperforms conventional classiﬁers. Exten-

sions of GLVQ by means of kernel functions have

been also investigated (Qin and Suganthan, 2004;

Sato, 2010), and the experiments reveal that the ex-

tended models achieve almost the same classiﬁcation

accuracy as SVM. However, only weights for the ker-

nels are trained, and positions of prototypes are never

changed in these models, like in SVM. This may lead

to the limit of classiﬁcation capability, and to the in-

crease of the number of prototypes.

It seems to be natural to train prototypes and their

weights simultaneously to achieve good classiﬁca-

tion performance with a fewer prototypes. A learn-

ing method of prototypes as well as weights has been

proposed (Karayiannis, 1996), but it cannot be suit-

able for classiﬁcation problems, because it was for-

mulated through unsupervised learning. One possible

alternative is to repeat adding and removing proto-

types during learning to decrease errors (Grbovic and

Vucetic, 2009), but the optimality cannot be ensured,

because the weights for the prototypes are estimated

by a heuristic approach.

In order to train prototypes and their weights

through supervised learning framework, this paper

presents a novel distance-based classiﬁer by utiliz-

ing the multiplicative inverse of Lorentzian mixture.

Lorentzian has been evaluated as a response function

instead of sigmoid in multi-layered neural networks

(Giraud et al., 1995), but in this paper, we utilize it

for nearest neighbor classiﬁers. We show that the pro-

posed classiﬁer can be regarded as a natural extension

of the conventional nearest neighbor rule. We also

show that prototypes and their weights can be trained

simultaneously by General Loss Minimization (Sato,

2010), which is a generalized version of learning cri-

terion used in GLVQ. Experimental results for UCI

machine learning repository (Blake and Merz, 1998)

151

Sato A. and Ishii M. (2013).

Inverse of Lorentzian Mixture for Simultaneous Training of Prototypes and Weights.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 151-158

DOI: 10.5220/0004240201510158

 SciTePress

reveal that the proposed method achieves almost the

same as or higher classiﬁcation accuracy than SVM,

while the number of prototypes is much less than that

of support vectors.

2 PROPOSED METHOD

2.1 Inverse of Lorentzian Mixture

Lorentzian, which is also known as Cauchy-

distribution, has the probability density function

p(x) =



(x− y)

+ γ



, (1)

where y is the peak location and γ is the half-width

at half-maximum. Then, the discriminant function

for class ω

using the mixture of Lorentzian in d-

dimensional space can be written as

(x) =

∑

i=1



kx− y

+ γ



, (2)

where α

≥ 0 is a weight for the i-th distribution, and

’s (i = 1, ··· ,m

) are regarded as prototypes. As-

suming that α

= 1, we can obtain a more simple

form

(x) =

∑

i=1

kx− y

+ b

, (3)

where 1/α

is replaced by b

for ease of description.

As shown in Fig. 1, the height (or weight) of each dis-

tribution in Eq. (3) is deﬁned only by the bias b

, so

the above assumption is found to be useful for simpli-

fying the mixture of Lorentzian.

Let us consider the dissimilarity form by taking

the multiplicative inverse of Eq. (3) as follows:

(x) =

(x)

∑

i=1



kx− y

+ b



1/p

, (4)

where p = −1. Since this equation is formulated by

using L

norm, we can extend it by taking appropri-

ate value for p < 0. For example, when p → −∞, we

can obtain the nearest neighbor rule using biased Eu-

clidean distance as follow:

lim

p→−∞

(x) =

min

i=1



kx− y

+ b



. (5)

Therefore, Eq. (4) can be regarded as a natural exten-

sion of the conventional nearest neighbor rule. If we

use (d+1)-dimensionalvectors deﬁned by X← (x,0)

and Y

← (y

), Eq. (4) can be rewritten as

(X;θ) =

∑

i=1



kX− Y



1/p

, (6)

0.2

0.4

0.6

0.8

-10 -5 0 5 10

1/(x*x+1)

1/(x*x+2)

1/(x*x+4)

1/(x*x+8)

Figure 1: Examples of Lorentzian using different values

for the bias. As the bias becomes larger, the height of the

Lorentzian becomes lower.

where θ = {Y

|k = 1,··· , K;i = 1,· ·· ,m

} denotes

a set of classiﬁer parameters. Therefore, to train the

(d + 1)-dimensional vectors {Y

} is to train both the

prototypes and ther biases, simultaneously.

2.2 Learning based on GLM

To estimate the values of classiﬁer parameters, Gen-

eral Loss Minimization (GLM) is employed, because

it is a general framework for classiﬁer design (Sato,

2010). GLM can deal with prior probabilities and

various losses as well as zero-one loss for multi-class

classiﬁcation problems, but more simpliﬁed form is

used in this paper. Employing zero-one loss and as-

suming that the prior probabilities are proportional to

the number of samples in each class, the total loss can

be written as follows:

L(θ) =

∑

n=1

∑

k=1

∑

j6=k

f(ρ

;θ))1(t

= ω

). (7)

where θ is a set of classiﬁer parameters, N is the num-

ber of training samples, K is the number of classes, x

is the n-th training sample, t

is the genuine class of

, ω

is the k-th class, and 1(·) denotes an indica-

tor function such that 1(true) = 1 and 1( false) = 0.

f(ρ

(·)) is a sort of a risk associated with assigning

to class ω

, and ρ

(·) is the misclassiﬁcation mea-

sure of x

deﬁned by

;θ) =

;θ) − d

;θ)

;θ) + d

;θ)

, (8)

where d

(·) and d

(·) are dissimilarity-based discrim-

inant functions of class ω

and class ω

, respectively,

having positive values. The value of ρ

(·) ranges be-

tween −1 and 1, and leads to a correct (wrong) de-

cision when it is negative (positive.) In other words,

if ρ

(·) is positive, we can know that x

falls into

a wrong decision region. The function f(·) is a loss

function with respect to the misclassiﬁcation measure.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

152

In this paper, the following semi-sigmoid function

is used, because it resembles the hinge loss used in

SVM:

f(ρ) =











1+ exp(−ξρ)

for ρ < 0,

(ξρ+ 2)/4 for ρ ≥ 0.

(9)

Since the slant of the loss function ξ(> 0) deﬁnes the

margin between classes, we have to tune it with care

(Sato, 2010).

In GLM, the classiﬁer parameters are estimated

by minimizing L(θ) based on gradient search. If we

employ the steepest descent method, θ is updated it-

eratively (t ← t + 1) as

(t+1)

= θ

(t)

+ ∆θ

(t)

, ∆θ

(t)

= −ε(t)

∂L(θ)

∂θ



θ=θ

(t)

(10)

until θ

(t+1)

≃ θ

(t)

, where ε(t) > 0 and t denotes time.

The differential of L(θ) can be derived as

∂L(θ)

∂θ

∑

n=1

∑

k=1

∑

j6=k

′

(ρ

;θ))

∂ρ

;θ)

∂θ

1(t

= ω

), (11)

where f

′

(·) denotes the differential of f(·) as follows:

′

(ρ) =

(

ξf(ρ)(1− f(ρ)) for ρ < 0,

ξ/4 for ρ ≥ 0.

(12)

Here, let us use (d+ 1)-dimensional vectors as shown

in Eq. (6). The differentiation of ρ

(·) in Eq. (11)

depends on the class to which the prototype belongs.

For Y

which belongs to the correct class ω

∂ρ

;θ)

∂Y

−4d

;θ)

;θ) + d

;θ)]



;θ)

− Y



1−p

− Y

), (13)

and for Y

which belongs to the wrong class ω

∂ρ

;θ)

∂Y

;θ)

;θ) + d

;θ)]



;θ)

− Y



1−p

− Y

). (14)

Therefore, the update rules are obtained by substitut-

ing θ ← Y

or θ ← Y

in Eq. (10). In practice, the

conjugate gradient method is used for optimizing the

parameters. Note that we can obtain the prototypes

and the biases which minimize the total loss, simulta-

neously, because Y

consists of y

and b

. In the ex-

periments, the initial values of the prototypes were de-

termined by using K-means algorithm for each class.

For the biases, the same value was assigned to each

before learning, and they were normalized to satisfy

the following constraint during learning, so that the

biases range within a limit:

∑

k=1

∑

i=1

= C

. (15)

The outline of the learning algorithm is summarized

in Algorithm I.

Algorithm 1: Learning of the proposed method.

INPUT: p, ξ, C, m

(k = 1,··· , K)

INITIALIZE: y

← K-means, b

= C



∑

(i = 1,··· ,m

;k = 1,··· , K)

while not converged do

· θ

(t+1)

= θ

(t)

+ ∆θ

(t)

, where L(θ

(t+1)

) ≤ L(θ

(t)

)

· b

← b

×C

∑

(i = 1,··· ,m

;k = 1,··· , K)

end while

OUTPUT: y

, b

(i = 1,· ·· ,m

;k = 1,· ·· ,K)

3 EXPERIMENTS

To demonstrate the effectiveness of the proposed

method, hereinafter referred to as ILM, two kinds

of experiments were conducted: one was for two-

dimensional artiﬁcial data, and the other was for the

UCI machine learning repository.

3.1 Preliminary Experiments

Preliminary experiments for two-class two-

dimensional artiﬁcial data were conducted to

evaluate the effects of hyperparameters in ILM.

Figure 2 shows examples of decision boundaries

using different values for p in Eq. (6) and C in

Eq. (15). Prototypes are shown by white circles, and

the same value is assigned to every bias in each ﬁgure

according to the constraint of Eq. (15). As the value

of p becomes smaller, the decision boundaries tend to

approximate Voronoi diagrams, because the decision

rule becomes similar to the nearest neighbor rule.

While, as the value of C becomes larger, they tend

to form more simple shapes, because the Euclidean

distance between a sample and a prototype becomes

to have a larger bias.

Figure 3 shows the decision boundaries after

learning by ILM. Cross and plus marks denote train-

ing samples for each class, and white circles denote

prototypes. Each ﬁgure corresponds to that shown

in the bottom row in Fig. 2, which was used as the

InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights

153

p = −1 p = −2 p = −4 p = −8

C = 0.0

C = 1.0

Figure 2: Examples of decision boundaries for two classes using different values for p and C in the proposed method.

Prototypes are shown by white circles, and the same value is assigned to every bias in each ﬁgure according to the constraint

of Eq. (15).

p = −1 p = −2 p = −4 p = −8

C = 1.0

Figure 3: Decision boundaries after learning by the proposed method. Cross and plus marks denote training samples for each

class, and white circles denote prototypes. Each ﬁgure corresponds to that shown in the bottom row in Fig. 2, which is the

initial state before learning.

0.001

0.01

0.1

1 2 3 4 5 6 7

Bias

Prototypes

p=-1

1 2 3 4 5 6 7

Prototypes

p=-2

1 2 3 4 5 6 7

Prototypes

p=-4

1 2 3 4 5 6 7

Prototypes

p=-8

Figure 4: The values of biases after learning, sorted in as-

cending order. Each graph corresponds to the result shown

in Fig. 3.

initial state before learning. Note that all training

samples were used as initial values of prototypes in

these experiments. As shown in the ﬁgures, the pro-

totypes which belongs to the blue class become closer

each other as p becomes smaller, and the decision

boundary tends to maximize the margin between the

two classes after learning. Therefore, ILM trained by

GLM can be regarded as a maximal margin classi-

ﬁer as discussed in the literature (Sato, 2010). Fig-

ure 4 shows the values of biases after learning. Each

graph corresponds to the result shown in Fig. 3. Since

the bias is deﬁned as the reciprocal of the weight

for Lorentzian, the smaller biases are more important

than larger ones, and the prototypes having larger bi-

ases can be removed. For example, the top three can

be removed for p = −1, and the top two can be re-

moved for p < −1. The decision boundaries after re-

moval were almost the same as shown in Fig. 3. Since

no difference was found to the eye, the ﬁgures after

removal are not shown in this paper.

3.2 UCI Machine Learning Repository

3.2.1 Experimental Setup

Experiments for the UCI machine learning repository

were conducted to evaluate the performance of ILM.

Some data preprocessing was employed beforehand

as used in the literatures (Meyer et al., 2003): 1) all

records containing any missing values were removed

from the dataset, 2) a binary coding scheme was used

for handling categorical variables, and 3) all metric

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

154

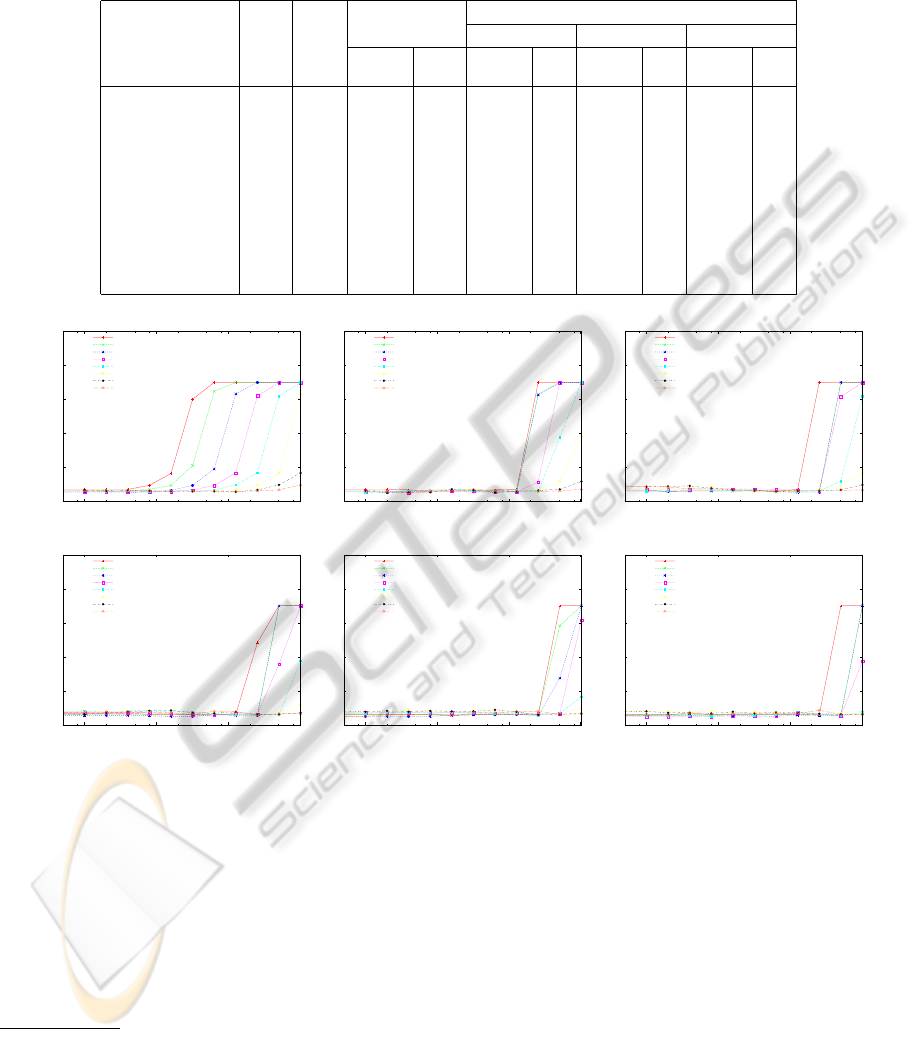
Table 1: Experimental results for UCI machine learning repository. “Ins.” denotes the number of instances after removing

missing data, “Att.” denotes the number of attributes excluding class attribute, and “#” denotes the number of support vectors

or prototypes. The proposed method, referred to as ILM, was evaluated with different parameter sets: some parameters were

ﬁxed as (a) C = 0, p = −2

, (b) C = 0, (c) p = −1, and the other parameters were varied.

SVM ILM

Dataset Ins. Att. (a) (b) (c)

Error # Error # Error # Error #

(%) (%) (%) (%)

BreastCancer 683 9 2.8 61 2.3 4 2.2 4 2.3 64

Cards 653 15 12.9 218 12.6 4 12.4 4 12.3 8

Heart1 297 13 14.1 139 13.5 8 13.5 8 13.1 2

HouseVotes84 435 16 3.7 102 3.7 2 3.4 8 3.2 4

Ionosphere 351 34 4.3 149 6.8 32 3.4 16 3.1 16

Liver 345 6 27.0 211 28.1 4 26.4 4 24.9 8

P.I. Diabetes 768 8 22.3 423 21.9 2 21.6 4 21.6 4

Sonar 208 60 11.5 154 8.7 32 7.7 32 11.1 8

Tictactoe 958 9 1.5 813 0.2 16 0.2 16 1.5 16

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

m=1 m=2 m=4

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

m=8 m=16 m=32

Figure 5: Error rates for BreastCancer in UCI machine learning repository by the proposed method with parameter set (c).

variables were scaled to zero mean and unit variance.

Nine datasets

as shown in Table 1 were evaluated

based on 10-fold cross validation. That is to say, the

data were divided into 10 partitions, and 9 partitions

were used for training and the rest was used for test-

ing. This process was then repeated 10 times, and

the obtained results were averaged to produce a single

estimation. All of the datasets are two-class classiﬁ-

The actual names in UCI machine learning reposi-

tory are Breast Cancer Wisconsin (Original), Credit Ap-

proval, Heart Disease, Congressional Voting Records, Iono-

sphere, Liver Disorders, Pima Indians Diabetes, Connec-

tionist Bench (Sonar, Mines vs. Rocks), Tic-Tac-Toe

Endgame, respectively.

cation problems, so that we can compare the perfor-

mance of ILM with SVM.

The proposed method has several hyperparame-

ters: p and m

in Eq. (6), C in Eq. (15), and ξ in

Eq. (9). In the experiments, the same number given

by m was used for m

(k = 1, ··· , K), so the per-

formance was evaluated using different values for p,

C, m and ξ. Speciﬁcally, p = {−2

|i = 0,· ·· ,8},

C = {0,2

|i = 0,· ·· ,10}, m = {2

|i = 0,· ·· ,5}, and

ξ = {2

|i = 1,· ·· ,8} were used.

InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights

155

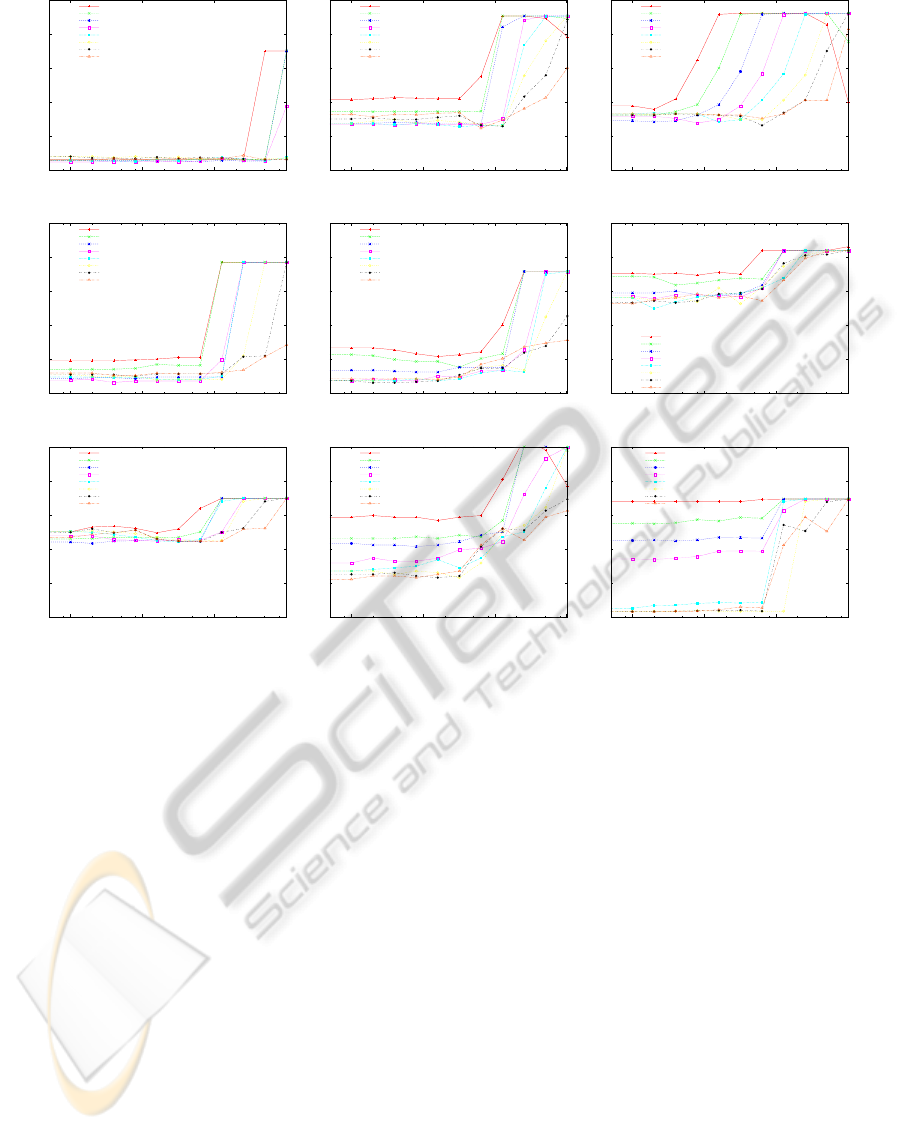
1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

BreastCancer (m=32) Cards (m=4) Heart1 (m=1)

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

HouseVotes84 (m=2) Ionosphere (m=8) Liver (m=4)

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

ξ=2

ξ=4

ξ=8

ξ=16

ξ=32

ξ=64

ξ=128

ξ=256

1 10 100 1000

Error (%)

Normalization Value for Bias

xi=2

xi=4

xi=8

xi=16

xi=32

xi=64

xi=128

xi=256

P.I.Diabetes (m=2) Sonar (m=4) Tictactoe (m=8)

Figure 6: Error rates for UCI machine learning repository by the proposed method with parameter set (c).

3.2.2 Experiment I

Results by ILM are shown in Table 1. The lowest er-

ror rates are listed for different parameter set: some

parameters were ﬁxed as (a) C = 0, p = −2

, (b)

C = 0, (c) p = −1, and the other parameters were var-

ied. Set (a) corresponds to GLVQ (p → −∞), set (b)

corresponds to an extension of GLVQ using L

norm-

based mixture, and set (c) corresponds to the multi-

plicative inverse of the linear mixture of Lorentzian.

Overall, the classiﬁcation accuracy for set (c) is bet-

ter than set (a) and set (b), except Sonar and Tictac-

toe. This means that the learning of biases is very ef-

fective to improve classiﬁcation accuracy, while the

norm-based mixture is also important for some

datasets. Figure 5 shows the error rates for Breast-

Cancer by ILM with set (c). The horizontal axis de-

notes the value of C, and the error rates using differ-

ent values for ξ are shown. It is noteworthy that the

lowest error in each ﬁgure is not so different. This

means that ILM does not seem to suffer from the over-

ﬁtting even though many prototypes are used. Fig-

ure 6 shows similar graphs to Fig. 5, but the best result

in various m was selected for each dataset. Note that

the number of prototypes by ILM as shown in Table 1

is just twice as many as the selected m.

Similar experiments by SVM were conducted for

comparison. Actually, SVM

light

was used for evalua-

tion. The hyperparametersin SVM are the trade-offC

and RBF parameter γ in K(x, y) = exp(−γkx− yk

The performance was evaluated using different values

for C and γ. Speciﬁcally, C = {2

|i = −5, ···12} and

γ = {2

|i = −10,··· ,5} were used. The lowest error

rates and the number of the obtained support vectors

are listed in Table 1. Clearly, the error rates by ILM

are lower than those by SVM, while the number of

prototypes is much less than that of support vectors.

For BreastCancer, the number of prototypes by ILM

tors, but the error rates stayed lower even though a

fewer prototypes were used. For example, it was 2.6

(%) for two prototypes (i.e. m = 1). Figure 7 shows

the results by SVM. These graphs are similar to Fig. 6,

but the horizontal axis denotes log

C, and the error

rates using different values for RBF parameter γ are

shown.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

156

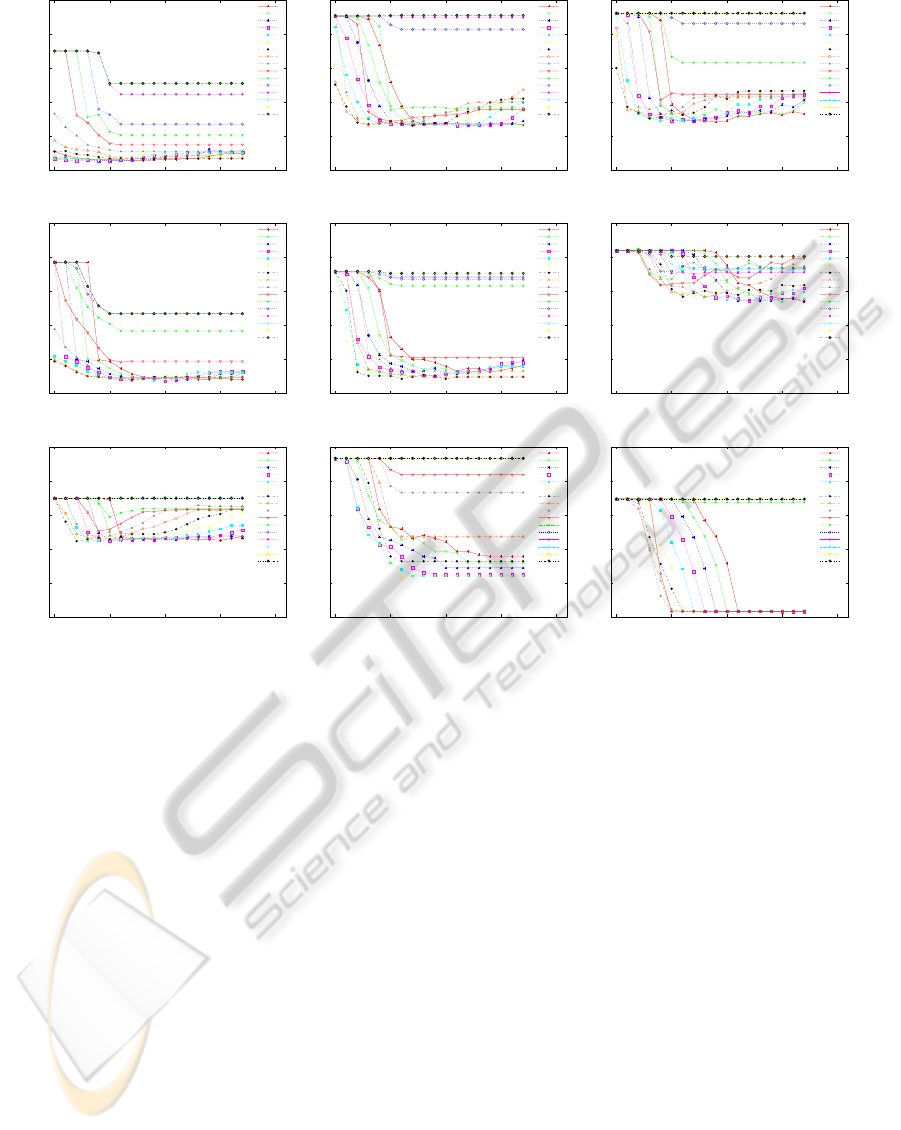
-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

BreastCancer Cards Heart1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

HouseVotes84 Ionosphere Liver

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

-5 0 5 10 15

Error (%)

log2(C)

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

P.I.Diabetes Sonar Tictactoe

Figure 7: Error rates for UCI machine learning repository by SVM with RBF kernel.

3.2.3 Experiment II

The results in Table 1 show that the proposed method

has capability to improve classiﬁcation accuracy for

any datasets used in the experiments. However, in

practice, the hyperparameters should be estimated

without testing data. Table 2 shows similar experi-

mental results for UCI machine learning repository,

but the hyperparameters in ILM and SVM were tuned

with only training data through two-fold cross valida-

tion. Of course, the error rates are slightly worse than

those in Table 1, but ILM retains almost the same as

or better performance than SVM on the whole.

4 DISCUSSION

Experimental results for UCI machine learning repos-

itory revealedthat ILM achievesalmost the same as or

higher classiﬁcation accuracy than SVM with a much

fewer prototypes than support vectors. The main ad-

vantage of ILM seems to train prototypes as well as

biases (or weights), while only weights are trained in

SVM. This may lead to reducing the number of pro-

totypes for achieving good performance. Since the

training of prototypes needs distance calculation at

every iteration in gradient search, it results in time

consumption as increasing the number of samples or

prototypes, or the dimensionality. In addition, the cost

function deﬁned by Eq. (7) does not seem to ensure

the convexity. However, as shown in the experiments,

ILM gives a good performance for real datasets, so

it can become one of the powerful methods for clas-

siﬁcation. It was also shown that prototypes having

larger biases can be removed without degrading per-

formance in the preliminary experiments, but this re-

dundancy removal should be investigated further.

5 CONCLUSIONS

A novel distance-based classiﬁer based on the multi-

plicative inverse of Lorentzian mixture was proposed,

which can be regarded as a natural extension of the

InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights

157

Table 2: Experimental results for UCI machine learning repository. Hyperparameters were tuned with only training data

through cross validation. “Ins.” denotes the number of instances after removing missing data. “Att.” denotes the number

of attributes excluding class attribute, and “#” denotes the number of support vectors or prototypes. The proposed method,

referred to as ILM, was evaluated with different parameter sets: some parameters were ﬁxed as (a)C = 0, p = −2

, (b)C = 0,

SVM ILM

Dataset Ins. Att. (a) (b) (c)

Error # Error # Error # Error #

(%) (%) (%) (%)

BreastCancer 683 9 2.8 66 2.5 32 2.6 64 2.6 64

Cards 653 15 13.6 189 13.2 8 13.9 8 14.6 4

Heart1 297 13 14.5 159 16.5 2 18.2 64 14.8 2

HouseVotes84 435 16 3.7 101 3.7 2 3.9 16 3.7 32

Ionosphere 351 34 4.8 148 8.3 8 3.7 32 4.3 64

Liver 345 6 28.1 203 28.1 4 27.5 4 26.3 4

P.I. Diabetes 768 8 22.3 418 22.5 2 22.3 32 21.9 64

Sonar 208 60 12.1 125 11.1 16 9.6 8 11.5 16

Tictactoe 958 9 1.7 349 1.7 2 0.9 16 1.7 2

conventional nearest neighbor rule. It was shown that

prototypes and biases can be trained simultaneously

by General Loss Minimization, which is a general

framework for classiﬁer design. The preliminary ex-

periments raised the possibility that prototypes having

larger biases can be removed without degrading per-

formance, but this redundancy removal should be in-

vestigated further. Experimental results for UCI ma-

chine learning repository revealed that the proposed

method achieves almost the same as or higher clas-

siﬁcation accuracy than SVM for all of nine datasets

with a much fewer prototypes than support vectors.

In future, the proposed method will be evaluated for

various classiﬁcation problems in real world.

REFERENCES

Blake, C. and Merz, C. (1998). UCI repository of machine

learning databases. University of California, Irvine,

Dept. of Information and Computer Sciences.

Cortes, C. and Vapnik, V. (1995). Support vector networks.

Machine Learning, 20:273–297.

Crammer, K., Gilad-Bachrach, R., Navot, A., and Tishby,

N. (2003). Margin analysis of the lvq algorithm. In

Advances in Neural Information Processing Systems,

volume 15, pages 462–469. MIT Press.

Giraud, B. G., Lapedes, A. S., Liu, L. C., and Lemm, J. C.

(1995). Lorentzian neural nets. Neural Networks,

8(5):757–767.

Grbovic, M. and Vucetic, S. (2009). Learning vector

quantization with adaptive prototype addition and re-

moval. In International Conference on Neural Net-

works, pages 994–1001.

Hammer, B. and Villmann, T. (2002). Generalized rele-

vance learning vector quantization. Neural Networks,

15(8–9):1059–1068.

Karayiannis, N. (1996). Weighted fuzzy learning vec-

tor quantization and weighted generalized fuzzy c-

means algorithm. In IEEE International Conference

on Fuzzy Systems, pages 773–779.

Kohonen, T. (1995). Self-Organizing Maps. Springer-

Verlag.

Meyer, D., Leisch, F., and Hornik, K. (2003). The support

vector machine under test. Neurocomputing, 55(1–

2):169–186.

Qin, A. K. and Suganthan, P. N. (2004). A novel ker-

nel prototype-based learning algorithm. In Inter-

national Conference on Pattern Recognition (ICPR),

pages 621–624.

Sato, A. (1998). A formulation of learning vector quantiza-

tion using a new misclassiﬁcation measure. In the 14th

International Conference on Pattern Recognition, vol-

ume 1, pages 322–325.

Sato, A. (2010). A new learning formulation for kernel clas-

siﬁer design. In International Conference on Pattern

Recognition (ICPR), pages 2897–2900.

Sato, A. and Yamada, K. (1996). Generalized learning vec-

tor quantization. In Advances in Neural Information

Processing Systems, volume 8, pages 423–429. MIT

Press.

Schneider, P., Biehl, M., and Hammer, B. (2009). Adap-

tive relevance matrices in learning vector quantiza-

tion. Neural Computation, 21(12):3532–3561.

Villmann, T. and Haase, S. (2011). Divergence-based vector

quantization. Neural Computation, 23(5):1343–1392.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

158