Analysis of Fault Injection in Implantable Capacitive Blood-pressure

Sensors

J. A. Miguel, Y. Lechuga and M. Martinez

Technology Electronics, Automatic and System Engineering Department, University of Cantabria,

Avda de los Castros s/n, Santander, Spain

Keywords: MEMS Testing, Fault Injection, Fault Modelling, Finite-element Analysis, Capacitive Pressure Sensor.

Abstract: This work explores the fault injection problem in the particular case of an implantable capacitive micro-

electromechanical pressure sensor for blood-flow measurement applied to the detection of in-stent

restenosis. In order to develop a MEMS testing method for this sensor and its related electronic circuitry, an

accurate and realistic fault model is essential. A behavioural description of the equivalent capacitance in the

fault-free case can be obtained from the analytical and numerical solutions of the deflection of a circular

diaphragm under a uniformly distributed pressure. However, the deflection problem for faulty conditions

due to, for example, contamination-based defects or partially released structures must be solved and

modelled using finite-element analysis.

1 INTRODUCTION

Vascular diseases are the leading mortality cause in

the European Union, being responsible of the 40%

of all deaths in the year 2008 (OECD, 2010). The

use of angioplasties and vascular stents has become

the most frequently used method for the treatment of

the most common vascular illness, such as blood

vessels stenosis, aortic aneurysms, arteriosclerosis

and renovascular hypertension.

However, in-stent restenosis (ISR), due to

neointimal tissue growth inside an implanted stent,

keeps on being the major drawback in stent

implantation, seriously compromising its long-term

results. The recent appearance of the so called

intelligent stents involves a potential economical

solution to this problem. An intelligent stent (e-

stent) incorporates a sensor capable of monitoring

and transmitting real-time measurements of

biological parameters related to blood-flow quality.

There are three typical approaches for designing the

aforementioned intelligent stents, regarding the

nature of the biological parameters and the way they

are measured: capacitive pressure measurements,

electromagnetic blood flow measurements and

ultrasonic blood flow measurements.

It is important to point out that an implantable

sensor for any of these techniques must match

certain characteristics, including reduced size, output

stability, low power consumption, low cost and

above all, reliability over extended time period. This

fact makes testing and thus, realistic fault injection

and fault modeling, a critical issue.

The objective of this work focuses on fault

model generation for an implantable capacitive

MEMS pressure sensor utilized to measure blood-

flow velocity. This model will allow the future

development of a comprehensive MEMS testing

methodology.

Continued success for MEMS will require cost-

effective methods of manufacturing. Advances in

this area must include a testing methodology that

allows products to be economically tested while

ensuring high quality and reliability. This is

especially important in applications where MEMS

are integral parts of safety-critical systems such as

implantable biomedical devices.

Traditionally, manufacturers focus on partially

checking the functionality of MEMS by performing

certain electrical, optical, mechanical or

environmental measurements (Wang et al., 2008).

However, there is a need to obtain correlations

between failure modes and the underlying physical

causes. These relationships will allow accurate

modeling of complex effects that can be used in fault

model generation, fault diagnosis and in the

development of efficient testing techniques.

153

Miguel J., Lechuga Y. and Martinez M..

Analysis of Fault Injection in Implantable Capacitive Blood-pressure Sensors.

DOI: 10.5220/0004241701530158

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2013), pages 153-158

ISBN: 978-989-8565-34-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Thus, success of any MEMS testing

methodology is highly dependent on the fault

models employed. Fault models that do not include

real defective behavior can reduce defect coverage,

degrade test quality and, therefore, the reliability of

the implantable sensor.

MEMS fault models must explicitly consider the

impact of defects on the micromechanical structures.

Our approach centers on the inductive generation of

the possible faulty behaviors from realistic finite-

element simulations. Particularly for those faults

whose behavior cannot be easily described by an

analytical model, as in the fault-free case.

Section 2 introduces the most common failure

mechanisms that can affect MEMS devices. In

Section 3 the capacitive pressure sensor chosen as

system under test is presented. Section 4 describes

the need of finite-element (FE) analysis for

modeling faults such as incomplete release of

suspended elements and contamination, in the case

of diaphragm or membrane-based MEMS pressure

sensors. Finally, in Section 5 conclusions are

presented.

2 FAILURE MECHANISMS AND

FAULT CLASSES

Among the failure mechanisms or defects which can

appear during fabrication, defects occurring during

the CMOS process can be distinguished from defects

occurring during micromachining (Castillejo et al.,

1998); (Mir et al., 2000); (Huang et al., 2012).

Microelectronic and micromechanical

components are created on the wafer during the

CMOS process by means of a set of semiconductor,

conductor and dielectric layers. These layers are

obtained through technological operations such us:

oxidation, deposition, photolithography, etching, ion

implantation or annealing. Each one of them is a

potential source of defects. Therefore, as a result of a

technological step, contaminants or residuals may

remain in the environment and be harmful in a

succeeding step.

For example, one of the most common problems

encountered for the fabrication of CMOS-

compatible MEMS is the presence of oxide residuals

in areas of naked silicon exposed for

micromachining. These oxide residuals can be

formed from thermal silica and from different layers

of oxides which have not been properly cleaned, and

can prevent the formation of an adequate cavity

during micromachining of the exposed silicon.

During micromachining, anisotropic etching

outside the foundry is used to suspend the structures.

For surface micromachining, a sacrificial layer of a

material such as silicon oxide, polysilicon, porous

silicon or aluminium is deposited. The

postprocessing operation removes this sacrificial

layer to suspend the microstructure. However, a

suspended microstructure may not be fully released,

or the cavity produced may be inadequate, due to

several mechanisms that include, not only the

presence of unwanted oxide residuals, but also

insufficient etching time, slow etching rate because

of an inadequate solution, re-depositions after

etching, or the formation of complex substances

from etching chemical reactions. These substances

may affect the quality of the solution, reducing

etching rate or appear stuck on the microstructure at

the end of the process.

Failure mechanisms can be classified according

to the physical properties or parameters of the

MEMS which are affected. In summary, each group

of faults (affecting the gauge that provides the actual

electrical interface or the microstructure that

suspends the gauge) is in turn classified in two

classes: catastrophic faults, which prevent any

system utilization, and parametric faults, for which

changes on geometrical or material parameters alter

microsystem performance.

Stiction to the bulk or the inadequate release due

to incomplete etching of a suspended structure can

mostly occur for both surface and bulk

micromachining. With such faults, a seismic mass

may remain stuck, for example, in the case of an

accelerometer, or the geometry and clamping

conditions of the membrane of a capacitive pressure

sensor may be significantly affected. Besides that,

particle contamination may also give rise to

catastrophic or parametric faults, depending on their

position, geometry, and size.

For example, highly anisotropic wet etching of

single crystal silicon is widely used to create

membranes. Impurities or small crystal lattice

defects in the bulk material encountered during this

process have been reported to cause pyramids on top

of the membrane that change its characteristics

(Landsberger et al., 1996). The maximum size of the

pyramids is dependent on the depth of the etch into

the bulk and at which depth the defect occurs. The

angles between the main crystal planes of single

crystal silicon determine the sidewall slope of a

pyramid. FE-based fault characterization is

particularly important for these defects whose real

effect over MEMS performance cannot be easily

derived from analytical expressions.

BIODEVICES2013-InternationalConferenceonBiomedicalElectronicsandDevices

154

3 CAPACITIVE PRESSURE

SENSOR

Blood flow measurement represents one of the most

common procedures performed in hospitals for the

monitorization of cardiovascular diseases. In this

sense, an intelligent stent that incorporates a sensor

capable of monitoring and transmitting real-time

measurements of biological related parameters for

its clinical consultation can help to detect in-stent

restenosis (ISR).

Among the three typical flow measurement

approaches compatible with intelligent stent design

(electromagnetic, ultrasonic and pressure-based) we

focus on the pressure-based measurement since it

provides not only a measurement of the blood-flow

velocity into an obstructed vessel, but also a

measurement of the absolute pressure in the vessel,

providing additional information to carry out ISR

monitorization.

The simplest implantable version of the pressure

sensor is made of a capacitive MEMS to measure

blood pressure, and an inductance to form the LC

tank that transmits the information by proximity

coupling (Takahata et al., 2006). This capacitive

MEMS approach allows the integration of the sensor

and the electronic circuits in the same silicon

substrate, decreasing the overall cost of the system.

The low energy requirements of its components help

to reduce the system size since it can be powered by

a wireless link.

The principle of operation of this kind of sensors

is based on the simple concept of a two parallel plate

capacitor, where the equivalent capacitance is

inversely proportional to the distance between the

plates. Actually, these sensors usually consist of a

fully clamped diaphragm membrane suspended over

a sealed cavity and a fixed backplate. Once some

pressure is applied to the flexible membrane, it

suffers a deformation that reduces the chamber size,

increasing the equivalent capacitance between the

two-plate structure.

Figure 1: Simplified cross-section of the capacitive sensor.

Fig. 1 shows a simplified cross-section of a

MEMS capacitive pressure sensor, based on a

deflecting diaphragm and a fixed backplate; where P

is the uniformly distributed pressure applied to the

diaphragm, w

is the deflection of the diaphragm

center, t

is the initial undeflected gap between the

plates and t

is the thickness of the diaphragm.

Once known the analytical expression of

deflection (in radial or geometric coordinates) of a

fully clamped circular or rectangular diaphragm, the

capacitance of the sensor can be analytically

calculated by:

y)w(x,-t

dxdyε

CC∆C 



(1)

Where C

is the capacitance of the undeformed

sensor, ε

is the dielectric permittivity of free space

and A is the area of the plates.

In this work we are going to focus on the case of

a circular diaphragm model in order to evaluate the

necessity of a finite-element analysis for accurate

fault injection and simulation.

3.1 Circular Diaphragm

The deflection of a circular diaphragm with fully

clamped edges can be analytically expressed as a

function of the radial distance from the center of the

plate (Timoshenko, 1940). To validate the analytical

model, the following assumptions must be

considered (Chang et al., 2002): (a) the material of

the diaphragm must have isotropic mechanical

properties; (b) the thickness of the metallic electrode

on the plate has to be smaller than the plate’s

thickness in order to be neglected; (c) the gap

between the flexible plate and the backplate needs to

be small compared with the lateral extents of the

plates, so that the electric field fringing effects can

be neglected; (d) the residual stresses in the flexible

plate are not taken into consideration. Once the

previous requirements have been fulfilled, the

relationship between the circular diaphragm’s

deflection and the radial distance can be stated as:

1ww(r)



























(2)

Where r is the distance from the center of the

diaphragm, a is the radius of the diaphragm and w

is the maximum center deflection.

The value of the maximum center deflection

presents different analytical approximations,

regarding the relationship between the deflection

AnalysisofFaultInjectioninImplantableCapacitiveBlood-pressureSensors

155

and the thickness of the diaphragm. Under small

deflection conditions (w

< 30% t

), the maximum

deflection of a circular thin plate with fully clamped

edges can be noted as:





16Et

ν13Pa





(3)

Where a is the radius of the diaphragm, P is the

applied pressure, and υ and E are the Poisson ratio

and the elasticity modulus of the diaphragm’s

material respectively.

Under large deflection conditions (w

> 30% t

the relationship between the maximum center

deflection of the plate and the uniformly applied

pressure can be denoted as a cubic equation:





0.488w

16Et

ν13Pa









(4)

It can be seen how equation (4) can be approximated

to (3) when w

<< t

. For this reason, equation (4)

can be used to simulate the behaviour of the sensor

in both small and large deflection circumstances.

4 FE FAULT INJECTION

Finite element analysis (FEA) techniques are

essential for the design of micromechanical

structures. FEA tools work at a low level, are

processor intensive and incompatible with electronic

circuit simulators. This means that the designer lacks

the modelling tools to design without extensive

experimentation. In this sense, other approaches are

required to enable closed-loop simulation of the

complete microsystem containing sensors or

actuators together with electronic feedback,

processing and biasing circuits. For this reason,

designers and test engineers are increasingly

concerned about the introduction of behavioural

languages developed for circuit modelling and

compatible with electric simulators.

The use of through and across variables enables

the simulation of forces and displacements (or other

physical quantities) in a similar way to currents and

voltages. Closed-loop, network type, simulations of

transducers and electrical circuitry within the same

simulation environment is therefore possible

(Teegarden et al., 1998); (Mukherjee et al., 1999).

For accurate fault simulation results, it is

essential for the faults model to be correct. We

propose the use of a finite-element CAD tool to

analyze the effect of defects that can occur during

the manufacturing process, or even during the useful

lifetime of a capacitive MEMS pressure sensor, to

establish which ones will give rise to a faulty

behaviour, and to accurately describe them, and the

whole system, by a electrical-compatible

behavioural model where future test methods can be

evaluated.

To enable fault simulation with a realistic

estimation of the fault coverage of a test method, a

complete library of fault models, based on actual

defects/failure mechanisms, has to be developed.

Because of its relatively small thickness and high

deflection, the diaphragm or membrane of the

capacitive pressure sensor is expected to be the most

vulnerable component regarding the appearance of

defects. It has therefore been chosen as the critical

element of the capacitive sensor. The sensor

simulated consists of a polysilicon diaphragm

(Young Modulus: E = 169 GPa; Poisson Coefficient:

υ= 0.22) with a thickness of 4µm, a radius of 350µm

and a sealed cavity of 2µm height.

A uniformly distributed pressure of 60 mmHg is

applied to the top of the membrane. This pulmonary

artery pressure value is related to a medical

condition of moderate stenosis.

Figure 2: Behavioural model vs finite element model.

A behavioural model for the membrane

deformation in the fault-free case has been

developed using the equations (2) and (4) under a

Matlab simulation environment. Fig. 2 shows the

deflection results regarding the distance from the

center of the membrane obtained with this

behavioural model compared to the ones from a FE

simulation. When building a FE model of the

membrane, we must consider it as a circular-shaped

thin plate, which is clamped on all edges in such a

way that no movement or rotation is allowed in all

directions (restricted in all degrees of freedom).

Fig. 2 shows that the error caused when using the

analytical approximation instead of the finite-

0 50 100 150 200 250 300 350

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Distance (um)

Deflection (um)

Deflection vs. Distance (@P=8kPa)

Matlab

Ansys

BIODEVICES2013-InternationalConferenceonBiomedicalElectronicsandDevices

156

element model becomes slightly higher as far as we

come closer to the center of the membrane. The

maximum deflection calculated through the Matlab

model has a value of 1.802 μm, whereas this result

reaches 1.785 μm for the FE model. However, the

accuracy of this approximation can be enhanced, if

needed, without mayor changes in its mathematical

formulation. Therefore, an analytical-based model

can be considered valid for modelling the fault-free

behaviour of the membrane.

Finite element simulation is also carried out on a

representation of the membrane with a defect

inserted. For different sizes and locations of defects

this is repeated and the deflection produced is

measured. Because of the symmetry of the

membrane, fault injection is only necessary all along

one radius of the membrane, simplifying fault

injection and reducing simulation time.

As said in Section 2 impurities or small crystal

lattice defects cause pyramids on top of the

membrane. The angles between the main crystal

planes of single crystal silicon determine the

sidewall slope of a pyramid (54.7º, the angle

between a {100} and a {111} plane in case of

anisotropic etching of a {100} oriented wafer). This

is therefore a fixed parameter. Altering the base

length of the pyramid, the size is also changed, since

the height of the pyramid is calculated from the

fixed sidewall slope (Landsberger et al., 1996);

(Rosing et al., 2002).

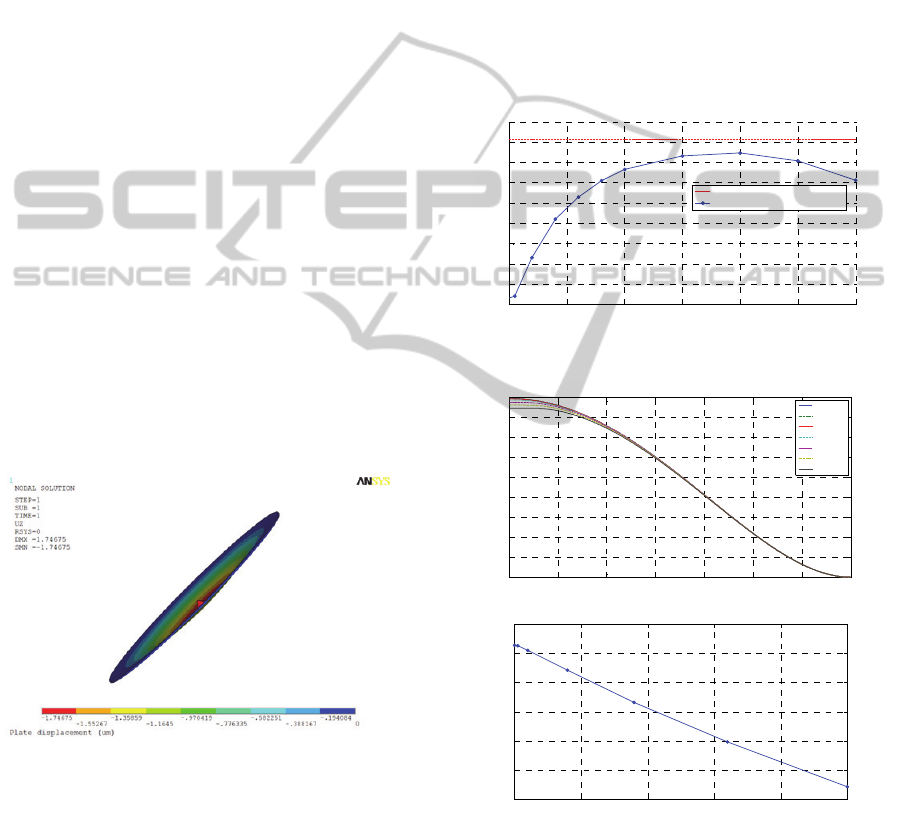
Figure 3: Screenshot of membrane with pyramid.

Pyramids on the membrane have been modelled

to have: a) the same size but locations all along a

radius of the membrane; and b) different sizes on the

same position in the centre of the membrane. An

example of a membrane with a pyramid, deflected

under the applied pressure, is given in Fig. 3. The

different colours are different regions of deflection

of the membrane.

Fig 4 shows the simulations of the displacement

of the center point of the membrane (maximum

deflection) in relation to different locations of a

pyramid (base side: 30 μm) over the radius line of

the membrane. We can highlight the significant drop

in displacement when the pyramid is located close to

the center of the membrane. Therefore the strongest

impact of a pyramid is produced at that location. If a

pyramid is located closer to the edge of the

membrane, the influence on the deflection gets

smaller. However second order effects related to the

proximity to the clamped edge and variations in the

effective geometry of the membrane (areas of

maximum stress) make the maximum deflection to

decrease, contrary to what could be expected, for

pyramids approaching the edge of the membrane.

Figure 4: Center deflection vs pyramid location.

Figure 5: Deflection for pyramids located at the center.

The next step is to place the pyramid in the

center of the membrane while only its size is varied.

The base length of the pyramids has been varied in

the range from 5 to 50 μm. The simulation results

are shown in Fig. 5. As can be seen in the lower

graph, the displacement of the centre point of the

0 50 100 150 200 250 300

1.745

1.75

1.755

1.76

1.765

1.77

1.775

1.78

1.785

1.79

Center Distance (um)

Max. Displacement (um)

Center Displacement vs. Pyramid Distance to the Center of the Plate (@P=8kPa)

DEFLECTION W/O. PYR

DEFLECTION W/. PYR (30x30)um

0 50 100 150 200 250 300 350

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Distance

(

)

Deflection (um)

Membrane Deflection vs. Pyramid Base Area (@P=8kPa)

PYR0U

PYR5U

PYR10U

PYR20U

PYR30U

PYR40U

PYR50U

0 500 1000 1500 2000 2500

1.68

1.7

1.72

1.74

1.76

1.78

1.8

Center Displacement vs. Pyramid Base Area (@P=8kPa)

Base Area (um

)

Max. Displacement (um)

AnalysisofFaultInjectioninImplantableCapacitiveBlood-pressureSensors

157

membrane approximates a linear function, as it

steadily decreases with increasing pyramid size. The

upper graph in Fig. 5 shows the membrane

deflection for different pyramid sizes. One important

aspect to point out is the constant maximum

deflection value for the membrane, not at a single

point, but under the complete pyramid base area.

This last effect cannot be modelled by using the

mathematical formulation presented in Section 3,

even if we modify it to increase its accuracy in order

to get closer to the results obtained by FE analysis.

Fig. 4 and Fig. 5 also show that the presence of a

pyramid on top of the membrane of our capacitive

MEMs pressure sensor produces a smaller deflection

than expected in the fault-free case. Thus, this faulty

condition implies a sensitivity loss of the sensor that

can compromise its reliability, which is a critical

issue for implantable devices.

Therefore, it is important to count on an accurate

behavioural model for its main component, the

membrane, valid for both fault-free and faulty

conditions. As said before, its deflection can have an

acceptable analytical solution in the fault-free case.

However, in this work we have proven that this

mathematical formulation is no longer valid for

modelling the membrane with certain kinds of faults

as, for example, the formation of pyramids on top of

the membrane. Therefore it is necessary to create

additional mathematical models that accurately

describe the behaviour of the membrane under faulty

conditions, considering the deflection results

obtained through FE simulations. Especially for

those faulty cases which significantly affect the

geometry and/or material properties of the

membrane.

5 CONCLUSIONS

In this work test-related problems for implantable

capacitive MEMS pressure sensors for the early

detection of in-stent restenosis have been presented.

The typical failure mechanisms and defects that can

give raise to the faulty behaviour of a

microelectromechanical system have also been

explained.

The deflection problem of circular membranes

has been proven to be analytically or numerically

solvable for a fault-free case, in order to build a

behavioural model of the sensor. Nevertheless, this

mathematical model is not valid to describe certain

faulty conditions where the geometry or the material

properties of the membrane are seriously affected.

So as to obtain a realistic fault model in these cases a

finite-element analysis must be performed.

REFERENCES

Castillejo A., Veychard D., Mir S., Karam J., Courtois B.,

Failure Mechanisms and Fault Classes for CMOS-

Compatible Microelectromechanical Systems, IEEE

International Test Conference, pp. 541–550, 1998.

Chang S.-P., Lee J.-B., Allen M.G., Robust capacitive

pressure sensor array, Sensors and Actuators A:

Physical, vol. 101, pp. 231–238, September 2002.

Huang Y., Vasan A. S. S., Doraiswami R., Osterman M.,

Pecht M., MEMS Reliability Review, IEEE

Transactions on Device and Materials Reliability, vol.

12, no. 2, pp. 482-493, June 2012.

Landsberger L. M., Nashed S., Kahrizi M., Paranjape M.,

On Hillocks Generated During Anisotropic Etching of

Si in TMAH, Journal of Microelectromechanical

Systems, vol. 5, no. 2, pp. 106-116, 1996.

Mir S., Charlot B., Courtois B., Extending Fault-Based

Testing to Microelectromechanical Systems, Journal

of Electronic Testing: Theory and Applications, vol.

16, pp. 279–288, 2000.

Mukherjee T., Fedder G. K., Blanton R. D., Hierarchical

design and test of integrated microsystems, IEEE

Design and Test of Computers, vol. 16 (4), pp.18–27,

1999.

OECD (2010), Health at a Glance: Europe 2010, OECD

Publishing. http://dx.doi.org/10.1787/health_glance-

2010-en

Rosing R., Reichenbach R., Richardson A., Generation of

component level fault models for MEMS,

Microelectronics Journal, vol. 33, pp. 861–868, 2002.

Takahata K., Gianchandani Y. B., Wise K. D.,

Micromachined antenna stents and cuffs for

monitoring intraluminal pressure and flow, Journal of

Microelectromechanical Systems, vol 15(5), pp. 1289–

1298, October 2006.

Teegarden D., Lorenz G., Neul R., How to model and

simulate microgyroscope systems, IEEE Spectrum 35

(7), pp. 66–75, 1998.

Timoshenko S., Theory of Plates and Shells, McGraw-

Hill, New York, 1940.

Wang L-T., Stroud C. E, Touba N. A., System-on Chip

Test Arquitectures. Nanometer Design for Testability,

1st. ed., Elsevier: Morgan Kaufmann Series, 2008.

BIODEVICES2013-InternationalConferenceonBiomedicalElectronicsandDevices

158