
Systematic Analysis of Structure of Multiple Tandem Repeat Arrays
in the Human Genome
Woo-Chan Kim and Dong-Ho Cho
Department of Electrical Engineering, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea
Keywords:
Repetitive Element, Tandem Repeat, Multiple Tandem Repeat Array, Systematic Analysis, Human Genome.
Abstract:
Repetitive elements constitute the vast majority of the human genome and form many complex but highly-
ordered patterns. Tandem repeats whose repeat units are placed next to each other particularly form very
highly structured patterns in the human genome when homologous multiple tandem repeats are close together.
In this paper, the structure of the multiple tandem repeat array (MTRA) is analyzed based on systematic
analysis. The proposed system for analyzing MTRA derives the original tandem repeat units by using the
characteristics of homology of MTRA and represents diagram model to show the structure of MTRA easily.
The analysis results of the four MTRAs in the human genome are shown and the proposed algorithm is proved
to be very efficient for analyzing MTRA by the comparison of three conventional algorithms.
1 INTRODUCTION
There are many repeated DNA sequences in the
genome of most organisms, which is called repeti-
tive element. The two major classes of repetitive el-
ements are interspersed repeats and tandem repeats.
Interspersed repeats are usually present as single
copies and distributed widely throughout the genome,
whereas tandem repeats are DNA sequences of which
repeat units are placed next to each other. Although
the functions of many repetitive elements have not yet
been known, their impact and importance on genomes
is evident. Mobile repeat elements have been a criti-
cal factor in gene evolution (Kazazian, 2004; Prak and
Kazazian, 2000). Also, some tandem repeats cause a
number of genetic diseases (Sinden, 1999) and they
have been used as genetic markers for human iden-
tity testing (Christian et al., 2001). Therefore, analyz-
ing repetitive elements is very important and we study
tandem repeats especially in this paper.
Tandem repeats are classified into three types,
which are satellite, minisatellite, and microsatellite.
Satellites form arrays of 1,000 to 10 million repeat
units particularly in the heterochromatin of chromo-
somes. Minisatellite form arrays of several hundred
repeat units of 7 to 100 bp in length. They are present
everywhere with an increasing concentration toward
the telomeres. Microsatellites are composed of units
of one to six nucleotides, repeated up to a length of
100 bp or more.
Although tandem repeats have been characterized
by some features, which are the position in the
genome, sequence, size, number of copies, and pres-
ence or absence of coding regions, there are much
more complex tandem repeats in the human genome.
In (Hauth and Joseph, 2002), the authors researched
complex pattern structures of variable length tan-
dem repeat (VLTR) and multi-periodic tandem repeat
(MPTR). Also, our previous studies to find and visual-
ize all repetitive elements in the genomes showed that
the structure of the unknown as well as known repet-
itive elements is very complex but highly organized
(Chung et al., 2011; Kim et al., 2012). We, here, fo-
cus on the structure of multiple tandem repeats, which
is called MTRA (Multiple Tandem Repeat Array).
MTRAs, which consist of multiple homologous
tandem repeats dispersed throughout specific se-
quence regions, are abundant in the genomes of hu-
man and mouse (Chung et al., 2011; Kim et al., 2012).
Despite of lack of research of MTRA, we expect that
MTRA plays an important role involving biological
functions from its abundance and unique structure.
Also, we can easily find a consensus tandem repeat
unit of an MTRA array since two or more tandem re-
peats are homologous. By getting a consensus tandem
repeat unit, we can find out how much the original
MTRA are broken, which can be used as an evidence
of the age of the genome.
We analyze four MTRAs from the human
genome, which are chromosome 7 (57,937,500
44
Kim W. and Cho D..
Systematic Analysis of Structure of Multiple Tandem Repeat Arrays in the Human Genome.
DOI: 10.5220/0004243300440052
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 44-52
ISBN: 978-989-8565-35-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

- 58,056,406 bp), chromosome 8 (46,832,500 -
47,458,334 bp), chromosome 22 (16,505,625 -
16,627,187 bp), and chromosome Y (25,000 -
117,031 bp). The method for getting a consensus tan-
dem repeat unit that are proposed in this paper is com-
pared with the three conventional programs or algo-
rithms, which are TRF (Tandem Repeat Finder) (Ben-
son, 1999), SRF (Spectral Repeat Finder) (Sharma
et al., 2004), and tandem repeat detection using PT
(Period Transform) (Buchner and Janjarasjitt, 2003;
Brodzik, 2007). TRF and SRF are the representa-
tive program for finding tandem repeat by using string
matching algorithm and signal processing algorithm,
respectively. A perfect MTRA is constructed by us-
ing the derived tandem repeat unit, and it is compared
with the original MTRA. Also, the structure of an
MTRA is shown in a diagram representation by us-
ing the consensus tandem repeat units.
2 SYSTEM MODELING AND
ALGORITHM
The modeling of MTRA consists of three stages,
which are TR Extractor, TR Analyzer, and MTR An-
alyzer. Fig. 1 shows the system structure for anal-
ysis of MTRA. TR Extrator gets each tandem repeat
from a given MTRA. The individual extracted tandem
repeat is analyzed by TR Analyzer. The analysis re-
sults of TR Analyzer are the original tandem repeats
as well as the properties of the individual tandem re-
peats such as repeat unit, number of repeat unit, and
homology. MTR Analyzer, then, analyzes the rela-
tionships among the individual tandem repeats by us-
ing the results of TR Analyzer.
TR Cutter
TR Multiple-
Aligner
TR Aligner
TR Analyzer MTR AnalyzerTR Extrator
Stage 1 Stage 2 Stage 3
Sub-stage 1 Sub-stage 2 Sub-stage 3
Figure 1: System structure for analysis of MTRA.
2.1 TR Extractor
There are one or more tandem repeats that are homol-
ogous each other in an MTRA. We assume that there
are N tandem repeats in an MTRA and each tandem
repeat has n tandem repeat units whose length is l.
Then, we can express i’th tandem repeat in an MTRA
as TR
i
(n,l). TR Extractor divides each tandem repeat
from an MTRA, which means that it gets all TR
i
(n,l)
for the MTRA. However, TR Extrator defines tandem
repeat when the number and the length of tandem re-
peat units is greater than δ
n
and δ
l
, respectively.
2.2 TR Analyzer
TR Analyzer derives a consensus tandem repeat from
each tandem repeat in an MTRA. TR Analyzer con-
sists of TR Aligner, TR Cutter, and TR Multiple-
Aligner. These three sub-stages are iteratively pro-
cessed for better performances.
2.2.1 TR Aligner
Two DNA sequence blocks which are a reference se-
quence and a target sequence are aligned, and the
identity of the two sequence blocks are recorded in
TR Aligner. If we assume that the length of the se-
quence block is B and a sequence block that begins
from i’th nucleotide base of a tandem repeat is S(i),
the reference sequence of the firstly performed TR
Aligner is generally S(1). Also, the target sequence
is moved from S(1) to S(x − B + 1) where x is the
length of the tandem repeat.
The alignment of the two DNA sequences is con-
ducted by dynamic algorithm or greedy algorithm
(Zhang et al., 2000). The identity of the two se-
quences as a result of the alignment is recorded to
I(i, j) where i is the index of the reference sequence
and j is the index of the target sequence. Since the
reference sequence is fixed in TR Aligner, I(i, j) is
a function for variable j. Then, I(i, j) of a perfect
tandem repeat becomes 1 when j = i + l × k and
1 ≤ i, j ≤ x where k is an integer since same sequence
blocks are arranged periodically in a perfect tandem
repeat. The identity may have its peak point even if
the tandem repeat is broken because it still has the at-
tribute of the repetition of the tandem repeat. By using
this characteristic of the identity of the tandem repeat,
we can get the index of each tandem repeat unit.
2.2.2 TR Cutter
The identity function of a broken tandem repeat is
generally fluctuated because its original perfect tan-
dem repeat is randomly broken by biological phe-
nomena such as insertion, deletion, and substitution.
Thus, TR Cutter performs two processes to derive the
index of each tandem repeat unit. First, TR Cutter
makes the identity function be smoothed by averag-
ing it locally. That is, a smoothed version of identity
function M(i, j) is defined as follows.
SystematicAnalysisofStructureofMultipleTandemRepeatArraysintheHumanGenome
45

Algorithm 1: Recursive process of three sub-stages of TR Analyzer: TR Aligner, TR Cutter, and TR Multiple-Aligner.
1: procedure TR ALINER(broken tandem repeat)
2: reference sequence index ← 0
3: consensus unit index ← −1
4: while reference sequence index ̸= consensus unit index do
5: Calculate identity function ◃ TR Aligner
6: Get all tandem repeat units ◃ TR Cutter
7: Get a consensus unit ◃ TR Multiple-Aligner
8: Substitute the index of the consensus unit to consensus unit index
9: end while
10: return consensus unit index
11: end procedure
M(i, j) =
∑
j+pW/2q−1
k= j−xW /2y
I(i, k)
W
(1)
where W is the smoothing window size.
The smoothing process removes the fluctuation of
the identity function so that only the start points of
real tandem repeat units have their local peak value of
identity. The smaller the window size of the smooth-
ing process is, the more peak points that are not the
start of tandem repeat unit exist. However, too large
window size of the smoothing process may remove
the local peak point of a real tandem repeat unit.
Therefore, the proper window size is required to leave
only the local peak points of the real tandem repeat
units in the smoothing process of the identity func-
tion.
Then, TR Cutter gets the start index of all the
tandem repeat units by differentiating the function
M(i, j). The differentiated function M
′
(i, j) of M(i, j)
is as follows.
M
′
(i, j) = M(i, j + 1) − M(i, j). (2)
After calculating M
′
(i, j), TR Cutter can find all
the tandem repeat units by recording the points when
M
′
(i, j) is 0.
2.2.3 TR Multiple-Aligner
The tandem repeat units that are gotten by TR Cut-
ter are aligned by TR Multiple-Aligner. By using
the multiple sequence alignment of the tandem repeat
units, TR Multiple-Aligner can get the consensus tan-
dem repeat unit. A direct method of the multiple se-
quence alignment is the dynamic programming tech-
nique to identify the globally optimal alignment so-
lution (Wang and Jiang, 1994; Just, 2001). However,
computational complexity of the direct method is ba-
sically too high, which takes O(l
n
) time where l and
n are the average length and the number of tandem
repeat units, respectively. Thus, we here use a sub-
optimal method that utilizes pairwise sequence align-
ment, which is similar to other suboptimal methods
(Humberto and David, 1998; Lipman et al., 1989).
In our method, all pairwise sequence alignments be-
tween each pair of tandem repeat units are performed,
and the tandem repeat unit that has the highest aver-
age alignment score with other tandem repeat units
is chosen as the consensus tandem repeat unit. The
proposed suboptimal method for finding the consen-
sus tandem repeat unit takes O((nl)
2
) time, which
reduces many computations compared with the dy-
namic programming technique particularly when l
and n are large.
After the consensus tandem repeat unit is chosen,
the three sub-stages of TR Analyzer, which are TR
Aligner, TR Cutter, and TR Multiple-Aligner, are re-
performed to get a more accurate consensus tandem
repeat unit. The recursive process of TR Analyzer is
conducted until the reference sequence is not changed
in TR Aligner. Algorithm 1 shows the pseudo code of
TR Analyzer.
2.3 MTR Analyzer
After TR Extractor divides all tandem repeats from
the target MTRA and TR Analyzer derives the con-
sensus tandem repeats of the individual tandem re-
peats, MTR Analyzer derives a consensus tandem re-
peat unit among all the tandem repeats. Sine the tan-
dem repeats in an MTRA are highly homologous and
are expected to be an identical tandem repeat origi-
nally, the consensus tandem repeat unit that is gotten
from the multiple tandem repeats increases the relia-
bility of the originality. Also, there are many reverse-
complement directional homologous tandem repeats
as well as forward directional homologous tandem re-
peats. Thus, we should not only consider the forward
direction but also the reverse-complement direction of
homology.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
46

The derivation of the consensus tandem repeat
unit is performed by multiple sequence alignment.
Thus, we also apply the sub-optimal method of mul-
tiple sequence alignment that is used in TR Multiple-
Aligner to the derivation of the consensus tandem re-
peat unit of MTRA for the purpose of reducing the
computational complexity.
We can describe an MTRA as a diagram by us-
ing the derived consensus tandem repeat units. Figure
2 shows an example of a diagram of an MTRA. The
MTRA shown in Figure 2 has two different tandem
repeat units and each tandem repeat appears twice.
The tandem repeats made by the first tandem repeat
unit are shown twice in forward and reverse direc-
tions, and then the tandem repeats made by the second
tandem repeat unit are shown twice in only forward
direction. Also, a region that is not a tandem repeat
exists between the two tandem repeats made by the
second tandem repeat unit. The four elements that are
written above tandem repeat unit in the diagram are
order, direction (F is forward direction and R is re-
verse direction), number of repetitions, and identity
in percentage. Also, the two elements below None
vertex is order and number of nucleotide bases.
TR1 TR2
None
1,F,50,95
2,R,40,90
3,F,20,78
5,F,30,75
4,350
Figure 2: Example of diagram representation of MTRA.
3 EXPERIMENTAL RESULTS
3.1 Analysis of MTRA of the Human
Genome
We analyzed four MTRAs of the human genome by
using the proposed system modeling. The analyzed
MTRAs are chromosome 7 (57,937,500 - 58,056,406
bp), chromosome 8 (46,832,500 - 47,458,334 bp),
chromosome 22 (16,505,625 - 16,627,187 bp), and
chromosome Y (25,000 - 117,031 bp). The human
genome were obtained from the NCBI (National Cen-
ter for Biotechnology Information) databases.
We first analyzed the repetitive elements and
repetitive element arrays of the DNA sequences by
using our analysis program, REMiner and REMiner
Viewer (Chung et al., 2011; Kim et al., 2012). The dot
plot patterns of repetitive elements and repetitive ele-
ment arrays of individual DNA sequences are shown
in Figure 3. According to the protocol of dot plot, a
square is the pattern of a tandem repeat and a rect-
angle shows the relationship between two tandem re-
peats (Chung et al., 2011; Kim et al., 2012; Edgar and
Myers, 2005).
(a) Human chr. Y
(25,000 ė 117,031 bp)
(b) Human chr. 22
(16,505,625 ė 16,627,187 bp)
(c) Human chr. 7
(57,937,500 ė 58,056,406 bp)
(d) Human chr. 8
(46,832,500 ė 47,458,334 bp)
Figure 3: Dot plot pattern of repetitive element arrays of the
human genome.
The MTRA of the human chromosome Y in Fig-
ure 3 (a) has two tandem repeats and they are homol-
ogous directly, whereas the two tandem repeats of the
MTRA of the human chromosome 22 are homolo-
gous inversely as shown in Figure 3 (b). Also, there
are many tandem repeats in the MTRA of the human
chromosome 7 but they are all homologous directly or
inversely as shown in Figure 3 (c). This means that the
tandem repeats all come from a same tandem repeat.
In Figure 3 (d), there are much more tandem repeats
and they come from two original tandem repeats.
The consensus tandem repeat units are derived as
results of our proposed analysis tool for MTRA. Ta-
ble 1 shows the consensus tandem repeat units of the
four target DNA sequences. The average identity is
SystematicAnalysisofStructureofMultipleTandemRepeatArraysintheHumanGenome
47
TR1 TR2
None
1,F,227,74
3,F,70,75
5,F,79,79
7,F,49,73
9,F,261,79
11,F,11,69
17,R,122,78
26,R,136,79
13,F,111,78
15,F,112,72
18,R,25,73
19,F,47,67
20,R,131,77
21,F,9,71
2,2550
4,6165
6,2790
8,34257
10,6883
12,2805
14,3588
16,1898
23,8066
TR1 None
1,F,305,94
3,F,185,95
2,60137
TR1
1,F,1300,86
2,R,1199,85
TR1 None
1,F,86,90
2,R,49,90
3,F,72,90
4,R,78,80
6,4299
8,4635
28,R,79,80
31,F,24,77
33,R,131,77
36,R,54,80
41,R,206,78
43,R,125,79
44,F,17,81
46,F,166,78
22,R,207,77
24,R,15,81
30,R,50,81
35,R,78,74
38,R,155,75
39,F,67,69
25,12553
27,1760
29,7418
32,3157
34,2265
37,1137
40,899
42,7986
45,1454
5,F,78,88
7,F,92,87
9,F,160,87
10,R,3,90
(a) Human chr. Y
(b) Human chr. 22
(c) Human chr. 7 (d) Human chr. 8
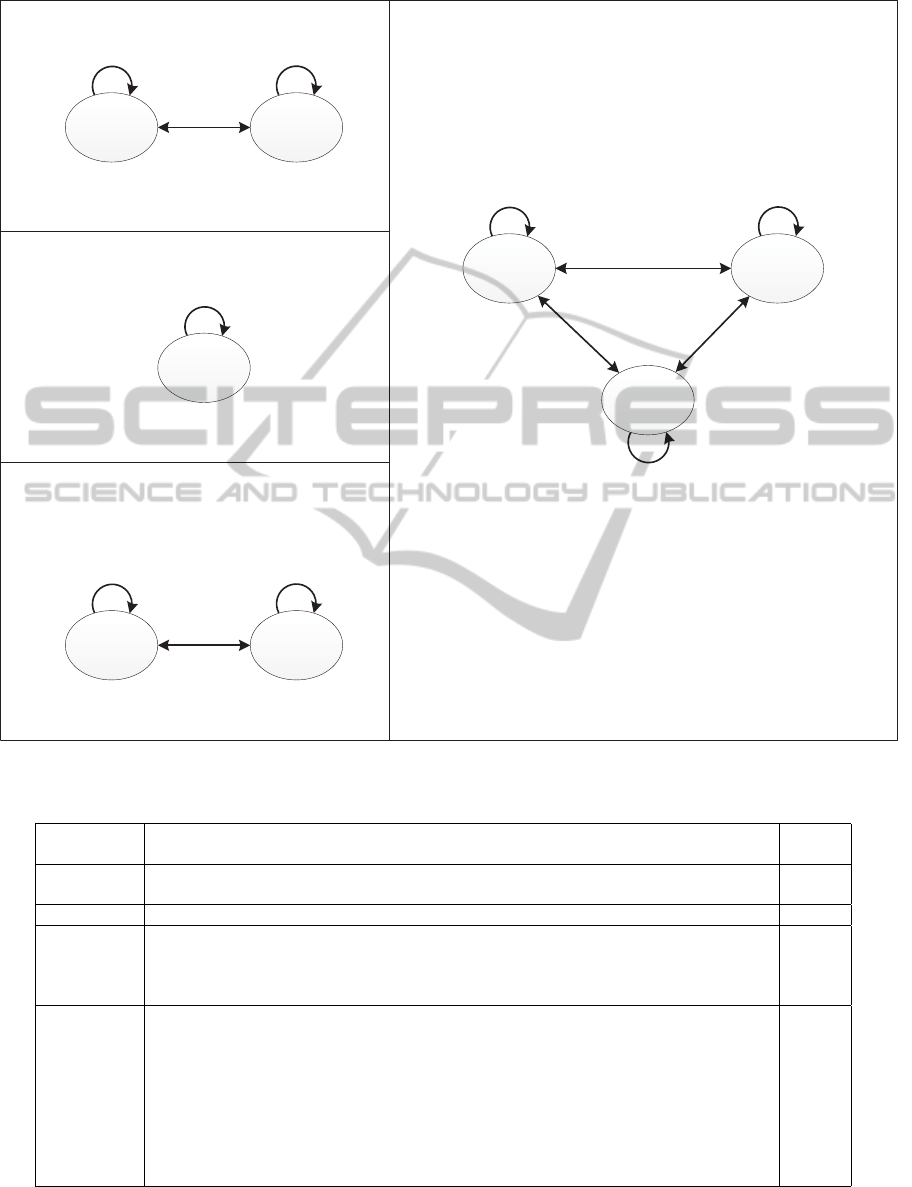
Figure 4: Diagram representation of MTRA of the human genome.
Table 1: Consensus tandem repeat units of each MTRA.
Human
Consensus tandem repeat unit
Average
Chromosome identity
Chr. Y
TR1: TAGGTCTCATTGAGGACAGATAGAGAGCAGA
0.95
CTGTGCAACCTTTAGAGTCTGCATTGGGCC
Chr. 22 TR1: GCAGCAGTGTTCTGGAATCCTATGTGAGGGACAAACACTCAGAACCCA 0.86
Chr. 7
TR1: TTCAACTCTGTGAGATGAATGCACACATCACAAAGAAGTTTCT
0.88
CAGAATGCTTCTGTCTAGTTTTTATGTGAAGATATTTCCTTTT
CCACCATAGGCCTCAAAGTGCTCCAAATGTCCACTTGCAGATT
CTACAAAAAGAGTGTTTCAAAACTGCTCAATCAAAAGAAAGG
Chr. 8
TR1: CCCACTGAGGCCTATAGTGAAAAACTGAATATCCCATGATAAA
0.76
AACTAGAAAGAAGCTATCTGTGAAACTGCTTTGTGATGTGTGC
ATTCAGCTCACAGAGTTAAACCTTTCTTTTGATTCAGCAGGTT
GGAAACACTCTTTTTGTAGAATCTGCAAGGGGATATTTGGAG
TR2: CCAAGGAGGCCTCTCCCATCCCAGAAGCCCCCAGGGCTGTCCCG
GGCGGGCTGTAAAGCCCCAGGCTTTGGAGCAGGGTGCCTGTGTC
TCTCGCAGAAGGCCCCCACAAGCGAAAACGGGGCCGCAGGGTG
GCGTGGGAGGGCCGCAGGGACTCAGGGGGACGTTGAGGCAGGC
AGAGGGGAGAAGCGGCGAGACTGCAGGGAATGCTGGGAGCCTC
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
48

Table 2: Comparison of consensus tandem repeat unit of proposed scheme and conventional schemes (Chromosome Y, 22,
and 7).
Human
Algorithm Consensus tandem repeat unit
Average Number
Chromosome identity of fails
Chr. Y
TR Analyzer
TAGGTCTCATTGAGGACAGATAGAGAGCAGA
0.95 0/2
CTGTGCAACCTTTAGAGTCTGCATTGGGCC
TRF
TAGGTCTCATTGAGGACAGATAGAGAGCAGA
0.95 0/2
CTGTGCAACCTTTAGAGTCTGCATTGGGCC
SRF
TAGGTCTCATTGAGGACAGATAGAGAGCAGA
0.95 0/2
CTGTGCAACCTTTAGAGTCTGCATTGGGCC
PTF
TAGGTCTCATTGAGGACAGATAGAGAGCAGA
0.95 0/2
CTGTGCAACCTTTAGAGTCTGCATTGGGCC
Chr. 22
TR Analyzer
GCAGCAGTGTTCTGGAATCCTATG
0.86 0/2
TGAGGGACAAACACTCAGAACCCA
TRF
GCAGCAGTGTTCTGGAATCCTATG
0.86 0/2
TGAGGGACAAACACTCAGAACCCA
SRF
GCAGCAGTGTTCTGGAATCCTATG
0.86 0/2
TGAGGGACAAACACTCAGAACCCA
PTF · · 2/2
Chr. 7
TR Analyzer
TTCAACTCTGTGAGATGAATGCACACATC
0.88 0/8
ACAAAGAAGTTTCTCAGAATGCTTCTGTC
TAGTTTTTATGTGAAGATATTTCCTTTTC
CACCATAGGCCTCAAAGTGCTCCAAATG
TCCACTTGCAGATTCTACAAAAAGAGTG
TTTCAAAACTGCTCAATCAAAAGAAAGG
TRF
TTCAACTCTGTGAGATGAATGCACACATC
0.88 0/8
ACAAAGAAGTTTGTCAGAATGCTTCTGT
CTAGTTTTTATGTGAAGATATATTCTTT
TCCACCATAGGCCTCAAAGTGCTCCAAA
TGTCCACTGCAGATTCTACAAAAAGAGT
GTTTGAAATTGCTCAATCAAAAGAAATG
SRF
TTCAACTCTGTGAGATGAATGCACACATC
0.79 2/8
ACAAAGAAGTTTCTCAGAATGCTTCTGTC
TAGTTTTTATGTGAAGATATTTCCTTTT
CCACCATAGGCCTCAAAGCGCTCCAAAT
GTCCACTTGCAGATTCTACAAAAAGAGT
GTTTAAAACTGCTCAATCAAAAGAAAGG
PTF
TTCAACTCTGTGAGGTGAATGCACATATC
0.80 6/8
ATAAAGAAGTTTGTCAGAATGCTTCTGTC
TAGTTTTTATGTGAAGATATATCCTTTT
CCACCATAGGCCCCAAAGTGCTCCAAAT
GTCCACTGCAGATTCTATAAAAATAGTG
TTTTAAAACTGCTCAATTAAAAGTAATG
the mean values of the identity between the perfect
tandem repeat that is made by the consensus tandem
repeat unit and individual broken tandem repeat. The
average identity shows the homology of each tandem
repeat in the MTRA and the brokenness level of the
MTRA, which can be graphically shown in Figure 3.
Based on the consensus tandem repeat units, we
describe each MTRA as a diagram in Figure 4. By
using the new representation of MTRA, we can eas-
ily see the overall structure of MTRA and the rela-
tionships among individual tandem repeats in MTRA.
Furthermore, the original perfect tandem repeat array
of the MTRA can be restored and the brokenness level
of the MTRA can be calculated by using the consen-
sus tandem repeat units.
3.2 Proposed Algorithm vs.
Conventional Algorithm
There are many conventional algorithms that find tan-
dem repeats although they did not consider multiple
homologous tandem repeats simultaneously. Most of
them can also derive the consensus tandem repeat unit
of a tandem repeat. Thus, the conventional algorithms
can be used to derive the consensus tandem repeat unit
of a tandem repeat that is the function of TR Analyzer
in our proposed system for the analysis of MTRA. In
this subsection, TR Analyzer is compared with the
SystematicAnalysisofStructureofMultipleTandemRepeatArraysintheHumanGenome
49

Table 3: Comparison of consensus tandem repeat unit of proposed scheme and conventional schemes (Chromosome 8).
Human
Algorithm Consensus tandem repeat unit
Average Number
Chromosome identity of fails
Chr. 8 (TR1)
TR Analyzer
CCCACTGAGGCCTATAGTGAAAAACTGAA
0.77 0/16
TATCCCATGATAAAAACTAGAAAGAAGCT
ATCTGTGAAACTGCTTTGTGATGTGTGCA
TTCAGCTCACAGAGTTAAACCTTTCTTT
TGATTCAGCAGGTTGGAAACACTCTTTT
TGTAGAATCTGCAAGGGGATATTTGGAG
TRF
CGCTTTGAGGCCTATGGTGGAAAAGGAAA
0.78 0/16
TATCTTCACATAAAAACTAGACAGAAGCA
TTCTCAGAAACTTCTTTGTGATGTGTGCA
TTCAACTCACAGAGTTGAACCTTCCTTT
TGATAGAGCAGTTTTGAAACACTCTTTT
TGTAGAATCTGCAAGTGGATATTTGGAG
SRF
CGCATTGAGGCCTATAGTGTAAAACTGAA
0.73 0/16
TATCCAGTGATAAAAACAAGAGAGAAGCT
ATCTGTGAACCTGCTTAGTGATATGTGGA
TTCAGCTCACATAGTTAAACCTTACTTTT
GATTCAGCTGTTTGTGGAAACACTCTTTT
TGTAAAATCTGCCAATAGACATTTCAAAG
PTF
CCCCCAAAGGCCAAAAGTCAAAATCTGAA
0.64 15/16
TATCCCGTGAAAAAAACTATAAAGAAAAT
ATCTGAGAAAATACTTTGTGGTGTAAAGA
GTCATCTCAGAGAGTTAAAACTTTCTTT
TGATAAAACAATTTGAAAAAACTTTTTT
GTAAAATCTCTGAAAGGTAATTTTAGAG
Chr. 8 (TR2)
TR Analyzer
CCAAGGAGGCCTCTCCCATCCCAGAAGCCCC
0.76 0/12
CAGGGCTGTCCCGGGCGGGCTGTAAAGCCCC
AGGCTTTGGAGCAGGGTGCCTGTGTCTCTCG
CAGAAGGCCCCCACAAGCGAAAACGGGGCCG
CAGGGTGGCGTGGGAGGGCCGCAGGGACTCA
GGGGGACGTTGAGGCAGGCAGAGGGGAGAAG
CGGCGAGACTGCAGGGAATGCTGGGAGCCTC
TRF
CCAAGGAGGCCTCTCCCATCCCAGAAGCCCC
0.71 3/12
AGGGCTGTCCCAGGCAGGCTGTAAAGCCCCA
GGCTTTGGAGCAGGGTGCCTGTGTCTCTCGC
GGAAGGCCCCACAAGCGAAAACGGGGTCGCA
GGGTGGCGTGGGCGGGTCACAGGGACTCAG
GGGACATTGAGGCAGGCAGAGGGGAGAAGC
AGCAAGACAGCAGGGAATGCTGGGAGCCTC
SRF
CCAGGAGGCCTCTCCCATCCCCGAAGCCCTC
0.69 2/12
AGGGCTGTCCCGGACTTGGTGTAAAGCCCCA
GGCTTTGGAGCAGGGTGACTGTGTCTCTGGC
GGAAGGCCCTGACAAGCGAAAACGGGGTAGC
AGGGTGGCGTGGGCGGGTCATGGGGACTCAG
CGGGACGTTGAGGAAGGCCGAGGGGAGAAGC
AGCAAGAAAGCAGGGAGTGCTGGGAGCCTC
PTF
TCAAGGAGGCCTCTCCCATTCCAGAAGCCCC
0.65 11/12
CAGGGCTGTTCCTGTTTGATTGTAACTCTTC
AGGCTTTGGATTAGGGTACCTGTGTCTCTGG
TGGAAGGGCCCCAAAAGCGAGACCCGGGGGC
AAGGTGGAAGGTGGCGGGGGCAGGGACCCAG
GGGAAAGCTGAGACAGGCGGAGGGGAGAAGT
GGGAAGACCTCAGGCAATGCTGGGAGCCTT
representative conventional schemes that derive the
consensus tandem repeat unit, which are TRF (Tan-
dem Repeat Finder) (Benson, 1999), SRF (Spectral
Repeat Finder) (Sharma et al., 2004), and tandem re-
peat detection using PT (Period Transform) (Buchner
and Janjarasjitt, 2003; Brodzik, 2007).
TRF is the representative program of string match-
ing algorithms for finding tandem repeat. It uses pat-
tern recognition criteria that is constructed statisti-
cally and it is the most widely used tool for identi-
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
50

fication of tandem repeat for its high accuracy. SRF is
the representative program of signal processing algo-
rithms to identify tandem repeat. It finds repetitions
by converting the target DNA sequence from time do-
main to frequency domain using Fourier transform.
The tandem repeat detection using PT, which is called
PTF in this paper, is one of the algorithms for detect-
ing tandem repeat based on signal processing. How-
ever, it does not use Fourier transforms but uses pe-
riod transform to find repetitions.
We performed experiments to derive the consen-
sus tandem repeat unit of each tandem repeat of the
human genome by using the conventional schemes.
Table 2 and Table 3 compare the results of our
proposed scheme with those of three conventional
schemes. Among the conventional schemes, TRF
finds the most exact consensus tandem repeat unit in
all the given tandem repeats, whereas PTF shows poor
performance to detect consensus tandem repeat units.
The number of fails in Table 2 and Table 3 means the
number of the cases that a consensus tandem repeat
is not detected because the given DNA sequence is
not determined to be a tandem repeat. Thus, PTF is
only usable to find the consensus tandem repeat units
of the tandem repeats of human chromosome Y. This
is because PTF does not consider the mutations of in-
sertion and deletion of nucleotide bases. Although the
performance of TRF is similar to TR Analyzer, TRF
is inadequate to find the consensus tandem repeat unit
of tandem repeats that are lengthy and highly broken
like TR2 of human chromosome 8 as shown in Table
2 and Table 3. Therefore, TR Analyzer is the most ap-
propriate tool to derive the consensus tandem repeat
unit to date, though there are many other tools that
can be substituted.
4 CONCLUSIONS AND FURTHER
WORKS
We proposed a system model for analyzing MTRA,
which derives the consensus tandem repeat units
based on the homology of the multiple tandem re-
peats and shows the structure of MTRA though a
simple diagram representation. The proposed sys-
tem model was performed on four MTRAs of the hu-
man genome, which are chromosome 7 (57,937,500
- 58,056,406 bp), chromosome 8 (46,832,500 -
47,458,334 bp), chromosome 22 (16,505,625 -
16,627,187 bp), and chromosome Y (25,000 -
117,031 bp). The algorithm for deriving a consensus
tandem repeat unit of a tandem repeat in the proposed
system model can be substituted by a conventional
scheme that finds tandem repeat. However, in view of
deriving an exact consensus tandem repeat unit, the
experimental results showed that the proposed algo-
rithm is the most appropriate for deriving a consensus
tandem repeat unit to date.
The analysis of MTRA was performed based on
the hypothesis that the homologous tandem repeats
of an MTRA are originated from a same tandem re-
peat and MTRAs are very important to biological
phenomenon. This hypothesis is sufficiently plausi-
ble considering the high identity of the homologous
tandem repeats of an MTRA and their highly struc-
tured unique patterns. However, since the hypothesis
should be verified biologically, we are going to per-
form the biological experiments of MTRA with the
systematic analysis.
REFERENCES
Benson, G. (1999). Tandem repeats finder: a program
to analyze dna sequences. Nucleic Acids Research,
27(2):573–580.
Brodzik, A. (2007). Quaternionic periodicity transform: an
algebraic solution to the tandem repeat detection prob-
lem. Bioinformatics, 23(6):694–700.
Buchner, M. and Janjarasjitt, S. (2003). Detection and vi-
sualization of tandem repeats in dna sequences. IEEE
Transactions on Signal Processing, 51(9):2280–2287.
Christian, M., Dennis, J., and John, M. (2001). Strbase:
a short tandem repeat dna database for the human
identity testing community. Nucleic Acids Research,
29(1):320–322.
Chung, B., Lee, K., Shin, K., Kim, W., Kwon, D., You, R.,
Lee, Y., Cho, K., and Cho, D. (2011). Reminer: a
tool for unbiased mining and analysis of repetitive el-
ements and their arrangement structures of large chro-
mosomes. Genomics, 98(5):381–389.
Edgar, R. and Myers, E. (2005). Piler: identification and
classification of genomic repeats. Bioinformatics,
21(Suppl. 1):i152–i158.
Hauth, A. and Joseph, D. (2002). Beyond tandem repeats:
complex pattern structures and distant regions of sim-
ilarity. Bioinformatics, 18(Suppl. 1):S31–S37.
Humberto, C. and David, L. (1998). The multiple sequence
alignment problem in biology. SIAM Journal on Ap-
plied Mathematics, 48(5):1073–1082.
Just, W. (2001). Computational complexity of multiple se-
quence alignment with sp-score. Journal of Computa-
tional Biology, 8(6):615–623.
Kazazian, H. (2004). Mobile elements: drivers of genome
evolution. Science, 303(5664):1626–1632.
Kim, W., Lee, K., Shin, K., You, R., Lee, Y., Cho, K., and
Cho, D. (2012). Reminer-ii: A tool for rapid iden-
tification and configuration of repetitive element ar-
rays from large mammalian chromosomes as a single
query. Genomics, 100(3):131–140.
Lipman, D., Altschul, S., and Kececioglu, J. (1989). A tool
for multiple sequence alignment. Proceedings of the
SystematicAnalysisofStructureofMultipleTandemRepeatArraysintheHumanGenome
51

National Academy of Sciences of the United States of
America, 86(12):4412–4415.
Prak, E. and Kazazian, H. (2000). Mobile elements and the
human genome. Nature Reviews Genetics, 1(2):134–
144.
Sharma, D., Issac, B., Raghava, G., and Ramaswamy, R.
(2004). Spectral repeat finder (srf): identification
of repetitive sequences using fourier transformation.
Bioinformatics, 20(9):1405–1412.
Sinden, R. (1999). Biological implications of the dna struc-
tures associated with disease-causing triplet repeats.
American Journal of Human Genetics, 64(2):346–
353.
Wang, L. and Jiang, T. (1994). On the complexity of mul-
tiple sequence alignment. Journal of Computational
Biology, 1(4):337–348.
Zhang, Z., Schwartz, S., Wagner, L., and Miller, W. (2000).
A greedy algorithm for aligning dna sequences. Jour-
nal of Computational Biology, 7(1-2):203–214.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
52
