
Classification of HEp-2 Staining Patterns in ImmunoFluorescence
Images
Comparison of Support Vector Machines and Subclass Discriminant Analysis
Strategies
Ihtesham Ul Islam, Santa Di Cataldo, Andrea Bottino, Elisa Ficarra and Enrico Macii
Dipartimento di Automatica e Informatica, Politecnico di Torino, Corso Duca degli Abruzzi 24, Torino, Italy
Keywords:
HEp-2 cells, Indirect ImmunoFluorescence, Staining Pattern Classification, Support Vector Machines,
Subclass Discriminant Analysis, Image Processing.
Abstract:
Anti-nuclear antibodies test is based on the visual evaluation of the intensity and staining pattern in HEp-2
cell slides by means of indirect immunofluorescence (IIF) imaging, revealing the presence of autoantibod-
ies responsible for important immune pathologies. In particular, the categorization of the staining pattern is
crucial for differential diagnosis, because it provides information about autoantibodies type. Their manual
classification is very time-consuming and not very reliable, since it depends on the subjectivity and on the
experience of the specialist. This motivates the growing demand for computer-aided solutions able to perform
staining pattern classification in a fully automated way. In this work we compare two classification techniques,
based respectively on Support Vector Machines and Subclass Discriminant Analysis. A set of textural features
characterizing the available samples are first extracted. Then, a feature selection scheme is applied in order
to produce different datasets, containing a limited number of image attributes that are best suited to the clas-
sification purpose. Experiments on IIF images showed that our computer-aided method is able to identify
staining patterns with an average accuracy of about 91% and demonstrate, in this specific problem, a better
performance of Subclass Discriminant Analysis with respect to Support Vector Machines.
1 INTRODUCTION
Indirect immunofluorescence (IIF) is an imaging
modality detecting abundance of those molecules that
induce an immune response in the sample tissue.
This technique uses the specificity of antibodies to
their antigen in order to bind fluorescent dyes to spe-
cific biomolecule targets within a cell. The screen-
ing for anti-nuclear antibodies by IIF is a standard
method in the current diagnostic approach to a num-
ber of important autoimmune pathologies such as sys-
temic rheumatic diseases as well as Multiple Scle-
rosis and Diabetes (Egerer, 2010). This screening,
which makes use of a fluorescence microscope, is typ-
ically done by visual inspection on cultured cells of
the HEp-2 cell line: the specialist observes the IIF
slide at the microscope (see Fig. 1 for an example),
and makes a diagnosis based on the perceived inten-
sity of the fluorescence signal and on the type of the
staining pattern. Fluorescence intensity evaluation is
needed for classifying between positive, intermediate
and negative samples. Then, specific staining patterns
on positive and intermediate samples reveal the pres-
ence of different antibodies and, thus, different types
of autoimmune diseases. Therefore, a correct descrip-
tion of staining patterns is fundamental for the differ-
ential diagnosis of the pathologies. Examples of the
six main staining patterns described by literature (ho-
mogeneous, fine speckled, coarse speckled, nucleo-
lar, cytoplasmic or centromere) are reported in Fig. 2.
They are distinguished as follows:
• Homogeneous: diffuse staining of the entire nu-
cleus, with or without apparent masking of the nu-
cleoli.
• Nucleolar: fluorescent staining of the nucleoli
within the nucleus, sharply separated from the un-
stained nucleoplasm.
• Coarse/Fine Speckled: fluorescent aggregates
throughout the nucleus which can be very fine
to very coarse depending on the type of antibody
present.
• Centromere: discrete uniform speckles through-
out the nucleus, the number corresponds to a mul-
tiple of the normal chromosome number.
• Cytoplasmic Fluorescence: granular or fibrous
fluorescence in the cytoplasm.
53
Ul Islam I., Di Cataldo S., Bottino A., Ficarra E. and Macii E..
Classification of HEp-2 Staining Patterns in ImmunoFluorescence Images - Comparison of Support Vector Machines and Subclass Discriminant
Analysis Strategies.
DOI: 10.5220/0004244100530061
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 53-61
ISBN: 978-989-8565-35-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

The manual classification of HEp-2 staining pat-
tern suffers from usual problems in medical imaging,
that is (i) the reliability of the results depends on the
specialist’s experience and expertise, and (ii) the anal-
ysis of large volume of images is a tedious and time-
consuming operation, translating into higher costs for
the health system. Studies report very high inter- and
intra-laboratory variability for this type of screening
(up-to 10%), that can be even higher in case of non-
specialized structures (Egerer, 2010). This variability
impacts on the reliability of the obtained results and,
most of all, on their reproducibility.
Thus, in the last few years reliable automatic sys-
tems for automating the whole IIF process have been
in great demand and several tools have been pro-
posed (Creemers,2011; Hsieh, 2009; Perner, 2002;
Sack, 2003; Soda, 2007). Nevertheless, the accurate
classification of the staining patterns still remains a
challenge.
Several classification schemes have been ap-
plied: among the others, learning vector quantiza-
tion (Hsieh, 2009), decision tree induction algo-
rithms (Perner, 2002; Sack, 2003), and multi-expert
systems (Soda, 2007). Unfortunately, direct compar-
ison of the results presented by different works is not
possible, since they are obtained on different datasets
and on different classes. However, it is worth noting
that textural features are generally acknowledged for
being the most appropriate for staining pattern classi-
fication.
In this work, we compare two techniques that clas-
sify the cells into one of the six staining patterns ad-
dressed by literature. The first is based on Support
Vector Machines (SVM). This approach was already
introduced in our previous work (Di Cataldo, 2012),
and it is described again here for the sake of com-
pleteness. The second technique is a novel procedure
based on Subclass Discriminant Analysis (SDA), a re-
cent dimensionality reduction method that has been
proven successful in different problems. SDA aims at
classifying a large number of different data distribu-
tions, whether they are composed by compact sets or
not, by describing the underlying distribution of each
class using a mixture of Gaussians. Since some of
the staining patterns are characterized by a not negli-
gible within-class variance, SDA can be a promising
method for their classification.
In our approach, an initial set of features, based
on statistical measurements of the grey-level distri-
butions and on frequency-domain transformations, is
used to characterize each cell. The dimension of this
feature vector is then reduced applying different pro-
cedures, aiming at selecting the feature variables that
are best suited to the classification with both SVM and
SDA.
After a description of the dataset employed for
training and testing our methods, Section 2, and a
description of the two classification techniques, Sec-
tion 3, this work presents in Section 4 a comparison
between the two methods in order to select the best
IIF classification technique. Discussion about results
and conclusions are presented in Sections 4.3 and 5,
respectively.
2 MATERIALS
Our dataset contains IIF images that are publicly
available at (MIVIALab, 2012). It consists of 14
annotated IIF images acquired using slides of HEp-
2 substrate at the fixed dilution of 1:80, as recom-
mended by the guidelines in (Tozzoli, 2002). The
images were acquired with a resolution of 1388x1038
pixels and a color depth of 24 bits. The acquisition
unit consisted of a fluorescence microscope (40-fold
magnification) coupled with a 50W mercury vapour
lamp and with a digital camera (SLIM system by Das
srl) having a CCD with square pixel of 6.45 µm side.
An example of the available images can be seen in
Fig. 1.
From these images, a set of samples of HeP-2 cells
have been extracted. Specialists manually segmented
each cell at a workstation monitor, labelling it with
the corresponding fluorescence intensity level (either
intermediate or positive) and staining pattern. The lat-
ter can be distinguished in the six classes described in
the introduction.
Figure 1: HEp-2 IIF image.
The dataset contains a total of 721 cells, 325 of
which with intermediate and 396 with positive fluo-
rescence intensity (see Table 1 for a full characteri-
zation).
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
54
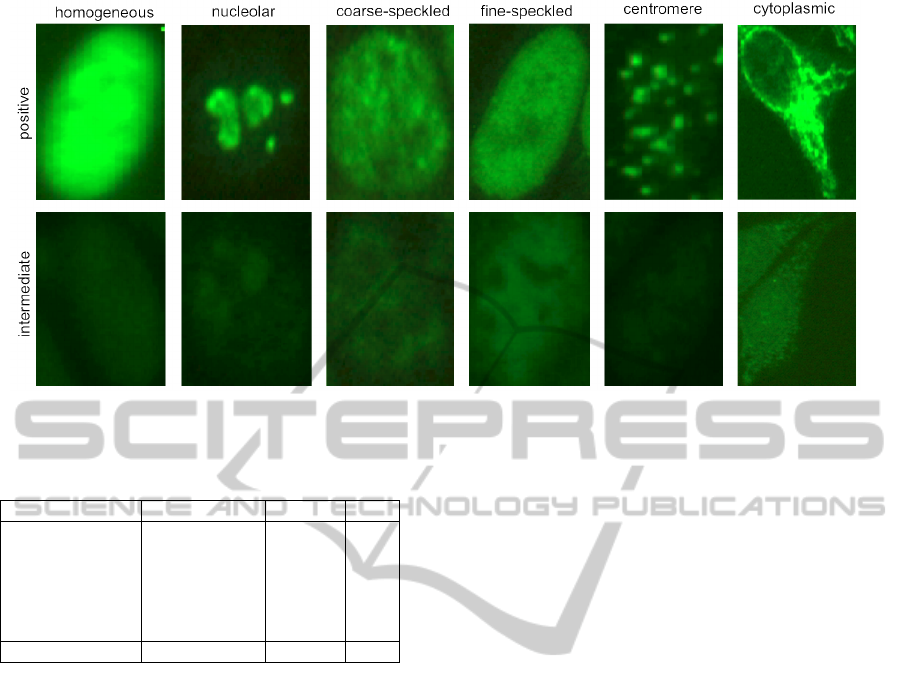
Figure 2: Examples of staining patterns that are considered relevant to diagnostic purposes, either with intermediate and
positive fluorescence intensity.
Table 1: HEp-2 cell dataset characterization.
Pattern n. of samples interm. pos.
Homogeneous 150 47 103
Nucleolar 102 46 56
Coarse speckled 109 41 68
Fine speckled 94 48 46
Centromere 208 119 89
Cytoplasmic 58 24 34
tot. 721 325 396
The staining pattern information provided by the
specialists was used as ground truth to assess the re-
sults of the proposed classifier.
3 METHODS
Our approach combines texture analysis and feature
selection techniques in order to obtain a limited set
of image features that is optimal for the classifica-
tion task. As already mentioned, for classification
we implemented and compared two different meth-
ods, based on SVM and on SDA.
In the following subsections we provide details
about all the steps of the proposed techniques.
3.1 Size and Contrast Normalization
In order to obtain image features independent from
variations of cell size and staining intensity, we ap-
plied size and contrast normalization to all the sam-
ples in our dataset. This avoided, as well, the neces-
sity of training two different classifiers, one for inter-
mediate and one for positive samples.
Size normalization was obtained by re-sampling
all the cell images to 64x64 pixels dimension. Con-
trast normalization consisted in linearly remapping
the intensity values so that 1% of data is saturated at
low and high intensities.
3.2 Feature Extraction
Textural analysis techniques have already been
proven successful in HEp-2 cell staining characteri-
zation (Di Cataldo, 2012). In fact, they are able to
describe the most relevant image variations occurring
in the cell allowing to differentiate between the stain-
ing patterns.
The two major approaches for textural analysis are
either based on statistical methods describing the dis-
tribution of grey-levels in the image or on frequency-
domain measurements of image variations. In our
work we propose a combination of both of them in
order to extract a comprehensive set of features able
to fully characterize the staining pattern of the cell.
A first set of features was computed based on
Gray-Level Co-occurrence Matrices (GLCM), a well
established technique that extracts textural informa-
tion from the spatial relationship between intensity
values at specified offsets in the image. More specif-
ically, textural features are computed from a set of
grey-tone spacial dependence matrices reporting the
distribution of co-occurring values between neigh-
bouring pixels according to different angles and dis-
tances (Haralick, 1973). In practice, the GLCM ele-
ment GLCM(i, j)
d,θ
contains the probability for a pair
of pixels located at a neighbourhood distance d and
direction θ to have gray levels i and j, respectively.
ClassificationofHEp-2StainingPatternsinImmunoFluorescenceImages-ComparisonofSupportVectorMachinesand
SubclassDiscriminantAnalysisStrategies
55

In our work, we extracted 44 GLCM textural fea-
tures, based on 16x16 GLCMs computed for a fixed
unitarian neighbourhood distance and a varying angle
θ = 0
o
, 45
o
, 90
o
, 135
o
(see (Di Cataldo, 2012) for de-
tails). The features are based on well-established sta-
tistical measurements whose characterization can be
found in (Haralick, 1973; Soh, 1999; Clausi, 2002).
The use of 4 different directions is aimed at making
the method less sensitive to rotations in the images.
Besides statistical methods, a largely used ap-
proach to extract relevant textural information for
image compression and classification is based on
frequency-domain transformations (Sorwar, 2001).
The underlying concept is the transformation to a dif-
ferent space whose coordinate system has an interpre-
tation that is closely related to the description of im-
age texture.
In our work, we computed the two-dimensional
Discrete Cosine Transform (DCT) (Ahmed, 1974)
of the normalized images and then extracted 328
DCT coefficients, which are described in details in
(Di Cataldo, 2012), representing different patterns of
image variation and directional information of the
texture. The same approach was already successfully
applied for texture classification and pattern recogni-
tion (Sorwar, 2001).
Combining GLCM and DCT sets, we obtained a
total number of 44 + 328 = 372 features to character-
ize each sample image.
3.3 Classification based on Support
Vector Machines
The first classification method we implemented was
already introduced in our previous work (Di Cataldo,
2012). It is based on Support Vector Machines
(SVM), a well-established machine learning tech-
nique that has been proven successful for classi-
fication and regression purposes in many applica-
tions (Chang, 2011).
The classification is based on the implicit map-
ping of data to a high-dimensional space via a kernel
function, and on the identification of the maximum-
margin hyperplane that separates the given training
instances in this space.
In our work we used SVM with radial basis kernel,
optimizing the kernel parameters by means of ten-fold
cross-validation technique and a grid search, as sug-
gested in (Chang, 2011).
3.3.1 Feature Selection
Feature selection (FS) strategies were applied in or-
der to select a limited set of optimal features able to
improve the accuracy of the staining pattern classifier.
SVM are widely acknowledged for their built-in
feature selection capability, as they implicitly map
data in a transformed domain where the features that
are crucial to the classification purpose are empha-
sized (Temko, 2006). Nevertheless, the combination
of SVM with feature selection strategies, besides im-
proving training efficiency, can further enhance the
accuracy of classification. In fact, although the pres-
ence of irrelevant features does not change the hyper-
plane margin of SVM, it may increase the radius of
the training data points, impacting on SVM’s gener-
alization capability and also increasing the probability
of over-fitting (Weston, 2000).
In our work we applied feature selection in two
sequential steps. The first is based on minimum-
Redundancy-Maximum-Relevance (mRMR) algo-
rithm, whose better performance over the conven-
tional top-ranking methods has been widely demon-
strated in the literature (Peng, 2005). The mRMR al-
gorithm sorts the features that are most relevant for
characterizing the classification variable, pointing at
the contemporaneous minimization of their mutual
similarity and maximization of their correlation with
the classification variable. The number of the candi-
date features selected by mRMR was arbitrarily set to
50.
As for mRMR to work at its best the classification
variables have to be categorical and not continuous,
we preventively performed features discretization on
the input data. For this purpose, we applied CAIM
(class-attribute interdependence maximization) algo-
rithm (Kurgan, 2004), which is best suited to work
with supervised data, as it generates a minimal num-
ber of discrete intervals by maximizing the class-
attribute interdependence.
The output of mRMR is a generic candidate fea-
ture set, which is independent from the classification
algorithm (Peng, 2005) and not necessarily optimal
for SVM. Therefore, we applied as second FS step a
Sequential Forward Selection (SFS) scheme in order
to iteratively construct the subset of optimal features
that is best suited for SVM classification.
Classical SFS works towards the minimization
of the misclassification error: starting from an ini-
tial empty set, at each iteration the feature pro-
viding the greatest classification accuracy improve-
ment is added, until no more improvement is ob-
tained (Ververidis, 2008). As this implementation
tends to be trapped in local minima, in our approach
we proceeded with the iterations until all the available
features were added, and then we selected the feature
set with the best classification accuracy. The final di-
mension of this optimal set was found to be 12 (see
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
56

Fig. 3).
Figure 3: Sequential Feature Selection strategy: misclassi-
fication error vs. number of selected features at each itera-
tion. The optimal feature set size is 12.
3.4 Classification based on Subclass
Discriminant Analysis
Discriminant analysis (DA) algorithms have been
used for dimensionality reduction and feature extrac-
tion in many applications of computer vision (Fuku-
naga, 1990; Swets, 1996; Etemad, 1997; Belhumeur,
1997). These algorithms project and map a set of sam-
ples X = (x
1
,x
2
,... ,x
n
), in a high-dimensional feature
space ∈ ℜ
D
and each with an associated class label
∈ [1,C], to a low-dimensional subspace ∈ ℜ
d
, with
dD, where the data can be more easily separated ac-
cording to their class-labels. Therefore, DA problem
can be generally stated as finding the transformation
matrix V = (v
1
,v
2
,. .. ,v
d
), with v
i
∈ ℜ
D
, for mapping
a sample x into the final d-dimensional subspace.
In most DA algorithms, the transformation matrix
V is found by maximizing the so-called Fisher-Rao’s
criterion:
J(V ) =
V
T
AV
|
V
T
BV
|
(1)
where A and B are symmetric and positive-defined
matrices, so that they define a metric. The solution
to this problem is given by the generalized eigenvalue
decomposition:
AV = BV Λ (2)
Where V is (as above) the desired transformation ma-
trix, and Λ is a diagonal matrix of its corresponding
eigenvalues.
Linear Discriminant Analysis (LDA) is probably
the most well-known DA technique. This method as-
sumes that the C classes the data belong to are ho-
moscedastic, that is their underlying distributions are
Gaussian with common variance and different means.
In (1), LDA uses A = S
B
, the between-class matrix,
and B = S
W
, the within-class scatter matrix, defined
as:
S
B
=
C
∑
i=1
(µ
i
− µ)(µ
i
− µ)
T
(3)
S
W
=
1
n
C
∑
i=1
n
i
∑
j=1
(x
i j
− µ
i
)(x
i j
− µ
i
)
T
(4)
where C is the number of classes, µ
i
is the sample
mean for class i, µ is the global mean, x
i j
is the j
th
sample of class i and n
i
the number of samples in class
i.
LDA provides the (C-1)-dimensional subspace
that maximizes the between-class variance and min-
imizes the within-class variance in any particular data
set. In other words, it guarantees maximal class sepa-
rability and, possibly, optimizes the accuracy in later
classification.
However, the assumption of having C ho-
moscedastic classes is the very limitation of this
method. LDA works well for linear problems and
fails to provide optimal subspaces for inherently non-
linear structures in data. Several extensions of LDA
have been introduced in literature to effectively clas-
sify data with non-linearities (Boulgouris, 2009).
To this end, one of the most effective approaches
is the Subclass Discriminant Analysis (SDA), pro-
posed in (Zhu, 2006). The main idea of SDA it is to
find a way to describe a large number of different data
distributions, whether they are composed by compact
sets or not, by describing the underlying distribution
of each class using a mixture of Gaussians. This
is achieved by dividing the classes into subclasses.
Therefore, the problem to be solved is to find the opti-
mal number of subclasses maximizing the classifica-
tion accuracy in the reduced space. In SDA, the trans-
formation matrix V is found by defining the between-
subclass scatter matrix S
B
in equation (1) as:
S
B
=
C−1
∑
i=1
H
i
∑
j=1
C
∑
k=i+1
H
k
∑
l=1
p
i j
p
kl
(µ
i j
− µ
kl
)(µ
i j
− µ
kl
)
T
(5)
where H
i
is the number of subclasses of class i,
µ
i j
and p
i j
are the mean and prior probability of the
j
th
subclass of class i, respectively. The priors are
estimated as p
i j
= n
i j
/n, where n
i j
is the number of
samples in the j
th
subclass of class i. In the simplest
case of SDA with no class subdivisions, this equation
reduces to that of LDA.
In order to select the optimal number of sub-
classes, in (Zhu, 2006), the authors propose two dif-
ferent methods. The first is based on a stability cri-
terion described in (Martinez, 2005). However, as
ClassificationofHEp-2StainingPatternsinImmunoFluorescenceImages-ComparisonofSupportVectorMachinesand
SubclassDiscriminantAnalysisStrategies
57

pointed out in (Gkalelis, 2011), when data have a
Gaussian homoscedastic subclass structure, the min-
imization of the metric used in this criterion is not
guaranteed. Authors in (Gkalelis, 2011) hypothesize
that this is likely to happen also for heteroscedastic
classes.
The second selection criterion is based on a
Leave-one-object test. In practice, for each subdi-
vision, a leave-one-out cross validation (LOOCV) is
applied, and the optimal subdivision is the one giving
the maximal recognition rate. The problem with this
strategy is that it has very high computational costs,
especially when the dataset to classify is large and the
number of classes is high. This is exactly what is hap-
pening in our case, where the initial classes are 6 and
the samples are 721.
Therefore, to overcome these problems, we used a
different formulation of the optimality criterion, sim-
ilar to the leave-one-object test, but based on a strat-
ified 5-fold cross validation, which optimizes the ac-
curacies obtained with a k-Nearest Neighbour (kNN)
classifier. A value of 8 for k has been heuristically
found to provide good classification results.
Our implementation differs from the original SDA
formulation for two other details. The first concerns
the clustering methods used to divide classes into sub-
classes. In (Zhu, 2006) data are assigned to subclasses
by first sorting the class samples with a Nearest-
Neighbour based algorithm and then dividing the ob-
tained list into a set of clusters of the same size. How-
ever, this method does not allow to model efficiently
the non-linearity present in the data, as in the case of
staining patterns under analysis. Therefore, we used
the K-means algorithm, which partitions the samples
into k clusters by minimizing iteratively the sum, over
all clusters, of the within-cluster sums of sample-to-
cluster-centroid distances. Since, in this method, the
centroids are initially set at random, different initial-
ization results in different divisions. Hence, we re-
peated the clustering 20 times and kept the solution
providing the minimal sum of all within-cluster dis-
tances.
The second difference is that, instead of increasing
the number of subclasses for each class of the same
amount at each iteration, all the possible permutation
of class subdivisions are created by iteratively incre-
menting by one the number of subclasses of a single
class in a set of nested loops. For a specific class r,
the subdivision process is stopped when the minimal
number of samples in the H
r
clusters obtained with K-
means drops below a predefined threshold. In order to
reduce the computational times, the clusters created
in inner loops are computed only once and cached for
further use.
The classification accuracy of our method is com-
puted as the average accuracy of the different CV
rounds. It should be underlined that, given the dif-
ferences between training and test sets, different op-
timal subclasses subdivision are likely to be obtained
at each CV iteration.
3.4.1 Feature Selection
As well as for the SVM classifier, we applied FS
strategies to SDA too. In this case, we used only the
reduced feature set obtained with mRMR. This has
been done for two reasons.
First, while mRMR is independent from the clas-
sification method, SFS relies on the classifier output,
which makes it unfeasible with the computational cost
of SDA.
Second, it can be easily shown that the rank of
matrix S
B
, and therefore of the dimensionality d of
the reduced subspace obtained from equation (2), is
given by min(H − 1, rank(S
X
)), where H is the to-
tal number of subclasses and rank(S
X
) is equal (or
minor) to the number of features characterizing each
sample. While the number of features selected with
mRMR (50) is a reasonable upper bound for d, reduc-
ing it further might hamper the possibility to obtain a
good classification accuracy in problems, like the one
tackled in this paper, in which the data present high
non-linearities.
4 RESULTS
The two classification methods presented in Section 3
were tested on the same annotated IIF images, using
the staining pattern information provided by the spe-
cialists as ground truth for cross-validation.
4.1 SVM Classification
We recall here the experimental results on SVM
classification, already reported in our previous pa-
per (Di Cataldo, 2012), for comparison with SDA ap-
proach.
As for SVM classification, experiments were run
on the following datasets:
dataset I, the initial 372 elements feature set;
dataset II, the 50 elements candidate set selected by
mRMR feature selection;
dataset III, the final 12 elements feature vector ob-
tained with combination of mRMR + SFS.
10-fold cross-validation accuracy results are re-
ported in Table 2, grouped by staining pattern. The
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
58

last row of the table reports the overall accuracy ob-
tained by SVM in each dataset.
Table 2: SVM Classification results: accuracy rate (%).
Pattern dataset I dataset II dataset III
Homogeneous 78.66 84.00 86.00
Nucleolar 89.22 93.14 93.14
Coarse speckled 92.66 95.41 98.17
Fine speckled 45.75 61.70 71.28
Centromere 84.13 88.46 87.02
Cytoplasmic 58.62 86.21 82.76
overall 77.95 85.58 86.96
These are the main considerations that arise from
analysing the results reported in Table 2:
• SVM classifier obtained an average accuracy of
86.96% in the six staining patterns. The max-
imum and minimum per-class accuracy were
98.17% (coarse speckled pattern) and 71.28%
(fine speckled pattern).
• the improvement of SVM classification accuracy
due to FS strategies was significant (+9.01% on
the overall average accuracy). This confirms the
considerations drawn in Section 3.3.1 about the
weakness of the implicit feature selection abil-
ity claimed by SVM. In particular, mRMR im-
proved the per-class accuracy of all the staining
patterns (see results on dataset II compared to
those on dataset I). The combination mRMR+SFS
(dataset III) further improved the average accu-
racy of SVM. While per-class accuracies of cen-
tromere and cytoplasmic patterns were slightly
decreased, the fine speckle pattern, that had low-
est per-class accuracy, is the class that obtained
the best improvement (+9.58% w.r.t. dataset II
and +25.53% w.r.t. dataset I). This non-uniform
behaviour is not surprising, since SFS optimized
the average classification accuracy in the over-
all dataset and not the accuracies of the single
classes.
4.2 SDA Classification
Table 3, which is, again, organized by staining class,
summarizes the classification results obtained with
SDA. As already explained in Section 3.4, SFS strat-
egy was not applied in combination with SDA clas-
sifier. Therefore, the table contains only results on
dataset I (the initial 372 feature set) and dataset II (50
feature set obtained after mRMR).
LDA results (which are those obtained with SDA
with no class subdivisions) are also provided for com-
parison, in order to demonstrate the effective capabil-
ities of SDA to better classify datasets with high non-
Table 3: SDA Classification results: accuracy rate (%).
dataset I dataset II
Pattern LDA SDA LDA SDA
Homogeneous 63.33 80.67 80.00 85.33
Nucleolar 90.29 94.29 91.19 96.14
Coarse speckled 87.19 88.05 92.55 91.69
Fine speckled 62.87 79.71 65.91 89.42
Centromere 75.96 73.53 80.78 82.17
Cytoplasmic 92.88 100.00 91.52 100.00
overall 78.75 86.04 83.66 90.79
linearities. Finally, in the last row we show the overall
accuracies obtained in the four cases.
Analysing the results, some considerations can be
drawn:
• as expected, the overall accuracy of SDA out-
performs that of LDA (+7.29% on dataset I and
+7.13% on dataset II). Concerning the per-class
results, better results are obtained in most of the
cases (except for centromere class for dataset I,
and coarse speckled class for dataset II), with, as
best improvements, a +17.34% in dataset I for ho-
mogeneous class and + 23.51% in dataset II for
fine speckled class;
• as in the SVM experiments, FS effectively im-
proves the SDA accuracies of all classes (the best
improvement being the +9.71% of fine speckled).
The overall improvement is +4.75%
• the best average accuracy obtained is 90.79%,
with dataset II, which outperforms the best accu-
racy obtained by SVM with mRMR+SFS feature
selection (86.96%, dataset III). The best per-class
improvements have been obtained for fine speck-
led (+18.14%) and cytoplasmic class (+17.24%),
while coarse speckled and centromere class ob-
tained slightly lower accuracies (respectively, -
6.48% and -4.85%).
4.3 Discussion
The results presented in Table 2 and 3 suggest that
the proposed algorithm, irrespective of the classifi-
cation technique actually applied, is a good solution
for the automated classification of immunofluores-
cence cell patterns. As a matter of facts, the accuracy
rate is comparable to the one obtained by the special-
ists, whose inter-laboratory variability is generally as-
sessed around 10% or even higher (Egerer, 2010). Be-
sides that, differently from human operators, our tech-
nique provides fully-repeatable results that are based
on objective and quantitative features of the images.
As for the classification techniques, the same re-
sults show that SDA technique, in combination with
ClassificationofHEp-2StainingPatternsinImmunoFluorescenceImages-ComparisonofSupportVectorMachinesand
SubclassDiscriminantAnalysisStrategies
59

a proper selection of the most relevant features, out-
performs the best accuracy achievable with SVM on
the same dataset (II) and even with those obtained by
SVM on dataset III, specifically optimized for that
technique with a two-step FS process. Therefore,
our experiments shows the capabilities of SDA to de-
scribe in a more precise way the underlying distribu-
tions of each of the staining pattern class, improving
their classification accuracies.
5 CONCLUSIONS
In this paper we proposed the comparison of two ap-
proaches, based on SVM and SDA, for the automatic
classification of staining patterns in HEp-2 cell IIF
images. Texture descriptors based on GLCM and
DCT coefficients are first exploited to extract a 372-
size characteristic vector for each cell. Then, a fea-
ture selection algorithm is applied to obtain a reduced
candidate feature set that improves the classification
accuracies of the two methods.
Feature selection is based on the mRMR algo-
rithm, which sorts the features that are most rele-
vant for characterizing the classification variable. The
50 top-ranked features were selected. In the case
of SVM-based method, a two-steps feature selection
procedure, coupling mRMR with SFS algorithm, is
implemented in order to further improve classification
accuracies.
The two approaches provide average classifica-
tion accuracies of about 87% and 91%, respectively.
These results are comparable with those of human
specialists. Conversely, they are completely repeat-
able since our automated technique does not depend
on the subjectivity of the operator. Moreover, our ex-
periments show the effectiveness of SDA into describ-
ing more precisely, compared to SVM, the underlying
distributions of each of the staining pattern class.
As future steps, we plan to work on:
1) a better characterization of cell patterns, which
can be insensitive to changes in size, rotation and in-
tensity;
2) an improvement of the SDA classifier in terms
of computational efficiency. For this purpose, meth-
ods selecting a priori the classes that effectively needs
to be partitioned, like the one described in (Sang-
Woon Kim, 2010), will be investigated;
Moreover, we plan to develop a pipeline for auto-
matic cells segmentation in IIF images and to com-
bine it with our pattern classification algorithm in or-
der to obtain a complete automated approach for the
computer-aided diagnosis (CAD) of autoimmune dis-
eases.
REFERENCES
Ahmed, N. and Natarajan, T. and Rao, K. R. Discrete
Cosine Transform. IEEE Trans. Computers, 90–93,
1974.
Belhumeur, P. N. and Hespanha, J. P. and Kriegman, D. J.
Eigenfaces vs. Fisherfaces: Recognition Using Class
Specific Linear Projection. IEEE Trans. Pattern Anal-
ysis and Machine Intelligence, vol. 19, no. 7, pp. 711-
720, July 1997.
Boulgouris, N. V. and Plataniotis, K. N. and Micheli-
Tzanakou, E. Discriminant Analysis for Dimensional-
ity Reduction: An Overview of Recent Developments.
In Biometrics: Theory, Methods, and Applications,
Wiley, 2009
Chang , C.-C. and Lin, C.-J. Libsvm: A library for support
vector machines. ACM Trans. Intell. Syst. Technol.,
2(3):27:1–27:27, May 2011.
Clausi, D. A., An analysis of co-occurrence texture statis-
tics as a function of grey level quantization. Can. J.
Remote Sensing 28(1):45–62, 2002.
Creemers, C. and Guerti, K. and Geerts, S. and Van Cot-
them, K. and Ledda, A. and Spruyt, V. HEp-2 cell
pattern segmentation for the support of autoimmune
disease diagnosis. ISABEL 2011, Proc. of, 28:1–5,
2011.
Di Cataldo, S. and Bottino, A. and Ficarra, E. and Macii,
E. Applying Textural Features to the Classification
of HEp-2 Cell Patterns in IIF images. 21st Inter-
national Conference on Pattern Recognition (ICPR
2012), Tsukuba, Japan, November 11-15, 2012.
Egerer, K. and Roggenbuck, D. and Hiemann, R. and
Weyer, M. G. and Buttner, T. and Radau, B. and
Krause, R. and Lehmann, B. and Feist, E. and
Burmester, G. R. Automated evaluation of autoan-
tibodies on human epithelial-2 cells as an approach
to standardize cell-based immunofluorescence tests.
Arthritis Research & Therapy, 12(2):1–9, 2010
Etemad, K. and Chellapa, R. Discriminant Analysis for
Recognition of Human Face Images. J. Optical Soc.
Am. A, vol. 14, no. 8, pp. 1724-1733, 1997.
Fukunaga, K. Introduction to Statistical Pattern Recogni-
tion. second ed. Academic Press, 1990.
Gkalelis, N. and Mezaris, V. and Kompatsiaris, I. Mixture
subclass discriminant analysis IEEE Signal Process-
ing Letters, vol. 18, no. 5, pp. 319-322, May 2011.
Haralick, R. M. and Shanmugam, K. and Dinstein, I.. Tex-
tural features for image classification. Systems, Man
and Cybernetics, IEEE Transactions on, 3(6):610–
621, nov. 1973.
Hsieh, R. Y. and Huang, Y. C. and Chung, C. W. and Huang,
Y. L. HEp-2 Cell Classification in Indirect Immuno-
fuorescence Images. ICICS 2009, Proc. of, 26:211–
214, 2009.
Kurgan, L. A. and Cios, K. J. Caim discretization algorithm.
IEEE Trans. on Knowl. and Data Eng., 16(2):145–
153, Feb. 2004.
Martinez, A. M. and Zhu, M. Where Are Linear Feature
Extraction Methods Applicable? IEEE Trans. Pattern
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
60

Analysis and Machine Intelligence, vol. 27, no. 12, pp.
1934-1944, Dec. 2005.
MIVIA Lab, http://nerone.diiie.unisa.it/zope/mivia/databas
es/db database/biomedical/ last accessed: September
2012.
Peng, H. and Long, F. and Ding, C. Feature selection based
on mutual information: criteria of max-dependency,
max-relevance, and min-redundancy. IEEE Trans
PAMI, 27:1226–1238, 2005.
Perner, P. and Perner, H. and Muller, B. Mining knowledge
for HEp-2 cell image classification. Artificial Intelli-
gence in Medicine, 26:161 –173, 2002.
Sack, U. and Knoechner, S. and Warschkau, H. and Pigla,
U. and Emmrich, F. and Kamprad, M. Computer-
assisted classification of hep-2 immunofluorescence
patterns in autoimmune diagnostics. Autoimmunity
Reviews, 2(5):298304, 2003.
Kim, S.-W. A pre-clustering technique for optimizing sub-
class discriminant analysis, Pattern Recognition Let-
ters, Volume 31, Issue 6, pp. 462-468, 2010
Soda, P. and Iannello, G. A Hybrid Multi-Expert Sys-
tems for HEp-2 Staining Pattern Classification. ICIAP
2007, Proc. of, 685–690, 2007.
Soh, L. and Tsatsoulis, C. Texture Analysis of SAR Sea
Ice Imagery Using Gray Level Co-Occurrence Matri-
ces IEEE Transactions on Geoscience and Remote
Sensing, 37(2), 1999.
Sorwar, G. and Abraham, A. and Dooley, L. S. Texture
Classification Based on DCT and Soft Computing.
FUZZ-IEEE01, Proc. of, 2-5 Dec 2001, 2001. 2011.
Swets, D. L. and Weng, J. J. Using Discriminant Eigenfea-
tures for Image Retrieval. IEEE Trans. Pattern Anal-
ysis and Machine Intelligence, vol. 18, no. 8, pp. 831-
836, Aug. 1996.
Temko, A. and Camprubi, C. N. Classication of acoustic
events using SVM-based clustering schemes. Pattern
Recognition, 39(4): 682–694, 2006.
Tozzoli, R. and Bizzaro, N. and Tonutti, E. and Villalta, D.
and Bassetti, D. and Manoni, F. and Piazza, A. and
Pradella, M. and Rizzotti, P. Guidelines for the lab-
oratory use of autoantibody tests in the diagnosis and
monitoring of autoimmune rheumatic diseases. Am J
Clin Pathol, 117(2): 316–24, 2002.
Ververidis, D. and Kotropoulos, C. Fast and accurate feature
subset selection applied into speech emotion recogni-
tion. Els. Signal Process., 88(12): 2956–2970, 2008.
Weston, J. and Mukherjee, S. and Chapelle, O. and Pontil,
M. and Poggio, T. and Vapnik, V. Feature selection for
SVMs. Advances in Neural Information Processing
Systems 13, 668–674, 2000.
Zhu, M. and Martinez, A. M. Subclass Discriminant Anal-
ysis. IEEE Trans PAMI, 28(8): 1274–1286, 2006.
ClassificationofHEp-2StainingPatternsinImmunoFluorescenceImages-ComparisonofSupportVectorMachinesand
SubclassDiscriminantAnalysisStrategies
61
