Detection of Sharp Wave Activity in Biological Signals using

Differentiation between Consecutive Samples

José L. Ferreira

, Pierre J. M. Cluitmans

1,2

and Ronald M. Aarts

1,3

Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands

Kempenhaeghe Epilepsy Center, Heeze, The Netherlands

Philips Research Laboratories Eindhoven, Eindhoven, The Netherlands

Keywords: Sharp Wave Activity Detection, Signal Slope Adaption, Electrocardiogram, QRS Detection.

Abstract: A number of signal processing techniques make use of first-derivative-based approaches for detecting

regions of interest in biological signals. For instance, central and five-point derivative-based algorithms are

employed for emphasizing and identification of the QRS complex in the ECG signal. Signal differentiation

approaches are also used for detection and removal of high-frequency components associated to artefacts in

the EEG signal. This paper aims to present a first-derivative approach based upon differentiation of

consecutive samples – signal slope adaption (SSD) – for detecting regions of sharp wave activity in

biological signals. A case study is analysed whereby SSD is used to mark and select the sharp wave activity

associated to the QRS complex in the electrocardiogram. Evaluation of our methodology reveals that SSD

shows to be effective for identification of QRS samples and, thereby, could be also employed to detect

samples associated to sharp wave activity regions of other biological signals which possess similar signal

slope behaviour.

1 INTRODUCTION

In research and clinical practice, automatic

measurement and recognition of parameters in

biological signals are fundamental to implement

computer-based tools for data analysis and patient

monitoring. In this context, detection of sharp wave

activity or instantaneous signal variability represents

a useful parameter in digital biological signal

processing. A classical example of identification of a

region with steep wave activity in biological signals

is the detection of the QRS complex for

measurement of the heart rate variability (HRV),

which constitutes an important method for

assessment of the cardiac regulation and diagnostic

of disorders such as arrhythmias and congestive

heart failure (Clifford, 2006); (Rangayyan, 2002).

A number of methodologies which make use of

first-derivative-based approaches and differentiation

of the ECG signal are proposed in the literature for

QRS detection (Pan and Tompkins, 1985);

(Hamilton and Tompkins, 1986); (Benitez et al.,

2000); (Köhler et al., 2002); (Rezk et al. 2011). The

basic idea of differentiating the digital signal is that

such a feature can be used for characterizing and

emphasizing regions of the signal which contain

sharp wave activity or specific slope features, as is

the case of the QRS complex (Köhler et al., 2002).

As mentioned by Rangayyan (2002), the QRS

complex has the largest signal slope in a cardiac

cycle due to rapid conduction and depolarization

characteristics of the ventricles. First-derivative

approaches are reported to be robust under

conditions of changes in QRS amplitude and for

ECG excerpts corrupted by baseline drifts, motion

artefacts, and muscular activity (Arzeno et al. 2008);

(Rangayyan, 2002); (Clifford, 2006).

Another first-derivative-based approach for fast

wave activity detection is associated with the

identification and removal of artefacts from the EEG

signal, as proposed by Van de Velde et al. (1998)

and Ferreira et al. (2012). According to Van de

Velde et al. (1998), a slope differentiator procedure

is employed for detection of the larger signal slope

related to the higher-frequency of muscles artefacts

components in comparison to the EEG. By using the

same idea, Ferreira et al. (2012) present an approach

based upon differentiation of consecutive samples of

the EEG signal for identification and removal of

gradient artefacts residuals from the

327

Ferreira J., J. M. Cluitmans P. and M. Aarts R..

Detection of Sharp Wave Activity in Biological Signals using Differentiation between Consecutive Samples.

DOI: 10.5220/0004245003270332

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 327-332

ISBN: 978-989-8565-36-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

electroencephalogram recorded within the fMRI

magnetic scanner. Thus, in both of the cases above,

the larger slope of the artefact interference is used to

identify whether or not a sample is artefact free.

First-derivative-based methods have the

advantage of not requiring manual segmentation of

data, training of the algorithms or patient-specific

modifications. Furthermore, they are often

implemented in real-time applications since they do

not require extensive computations (Arzeno et al.,

2008). Signal first-derivative-based approaches can

be used for identifying determined frequency

properties in the signal as well (Cluitmans et al.,

1993); (Van de Velde et al., 1998).

2 OBJECTIVES

Allen et al. (1998) propose a methodology for

ballistogram artefacts removal from the EEG signal

recorded during combined EEG-fMRI which makes

use of R-peaks detection in the ECG signal

simultaneously registered. The ballistogram or pulse

artefact is induced in the electrodes of the

electroencephalograph by the pulsatile movement of

blood in scalp arteries within the magnetic static

field (B

) of the magnetic scanner. According to

Allen et al., the identified QRS peaks in the ECG

signal are used to calculate an average pulse artefact

in the EEG signal which is then subtracted from

those regions where the ballistogram artefact

appears. A procedure to extract the ECG peaks

based upon data segmentation and training is

proposed within the methodology for average pulse

artefact subtraction by those authors.

During application of our method proposed in

Ferreira et al. (2012) for identification and removal

of residual gradient artefacts from the EEG signal,

we noticed that the same approach could be

modified and used for detection of the sharp wave

activity associated to the ECG peaks, as well as to

other types of biological signals. Thereby, it could

be used during removal of the ballistogram artefact

according to the methodology of Allen et al. (1998).

Moreover, the advantages mentioned by Arzeno et

al. (2008) by using first-derivative techniques could

be incorporated to that methodology.

The objective of this paper is to propose and

assess an approach for sharp wave identification in

biological signals which makes use of the difference

between consecutive samples of the signal, modified

from Ferreira et al. (2012). In this sense, a case study

is presented in which our method is applied to

identify the sharp wave activity associated to the

QRS complex of the ECG signal.

3 MATERIALS AND METHODS

3.1 Subjects

For application and evaluation of the proposed

methodology for fast wave activity detection, we

used data from the MIT-BH Arrhythmia and the

MIT-BH Noise Stress Test databases (MIT-BIH,

1998). These databases consist of 30 min

ambulatory ECG recordings whose sampling rating

for signal acquiring was 360 samples per second.

For performance evaluation purposes, we

implemented and applied a QRS detector using our

methodology to the 12 recordings of the MIT-BH

Noise Stress Test Database.

3.2 Differentiation between

Consecutive Samples for Sharp

Wave Activity Detection

Ferreira et al. (2012) describe a methodology for

identification and removal of gradient artefact

residuals from the EEG signal which is based upon

the differentiation of consecutive samples of the

digital signal. According to such an approach, the

larger slope associated to the sharp wave activity of

the gradient artefact residuals is used for detecting

EEG samples which contain artefact interference. In

order to identify which samples are in the region of

fast wave activity, a slope threshold (thrs) is

estimated in such a way that if the sample has signal

slope larger than this threshold, it is then classified

to belong to the sharp wave activity region. thrs can

be estimated, for example, taking into account the

probability distribution of the signal slope.

The same idea can be applied for other types of

biological signal with regions of sharp wave activity.

It is the case of the QRS complex whose samples

have signal slope much larger than other regions of

the ECG signal (Rangayyan, 2002). The signal of

figure 1a consists of an excerpt of 3600 samples

(10 s) of the MIT-BH Arrhythmia Database

recording 103. The respective differentiated signal is

shown in figure 1b. Such a differentiation was

obtained by subtraction of consecutive samples of

the ECG signal, diff (ECG). Clearly, it can be

noticed that higher values of the differentiated ECG

are coincident with the region of the QRS complex.

By analysing probability distributions of the

signal slope of standard clinical ECG signals with

high SNR, we could infer that the slope of samples

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

328

which belong to QRS regions are located above the

threshold, thrs, calculated considering the average

and the standard deviation of diff (ECG):

)(

)(diff)(diff

σμthrs

ECGECG





(1)

where μ

diff (ECG)

is the average and σ

diff (ECG)

is the

standard deviation of diff (ECG), considering a

window whose number of points is equal to the

length of the differentiated ECG. It is noteworthy

that the parameter thrs also corresponds to the RMS

value of diff (ECG).

808 809 810 811 812 813 814 815 816 817

-1

-0.5

0.5

1.5

ECG signal

Signal (



Tim e(s)

0 500 1000 1500 2000 2500 3000 350

-0.5

0.5

Sam

Diff (ECG) (



V/sample)

Differentiated ECG signal

Figure 1: (a) Excerpt of 3600 samples (10 s) of the MIT-

BH Arrhythmia Database recording 103 and (b) respective

differentiated signal diff (ECG).

Taking into account the remarks above, a

modified methodology from Ferreira et al. (2012),

herein named signal slope adaption (SSD), was

developed and is employed in this work in order to

carry out the localization of the sharp wave activity

associated to the QRS complexes, described as

follows.

As mentioned earlier, the highest values of the

signal differentiation, diff (ECG), occurs precisely

for samples located in the QRS complex. Therefore,

once the highest slopes of the ECG signal can be

associated to QRS samples along the ECG signal,

they could be adequately identified.

The maximum absolute value of the difference

between consecutive samples of the ECG signal

corresponds to the parameter r

which is related to

diff (ECG) by the following expression:





max

r diff ECG

(2)

where i is the subscript of the maximum slope within

diff (ECG).The two consecutive samples ECG

and

ECG

i+1

associated to r

are adapted by using (3):

iii,corct

LECGECG 



iii,corct

LECGECG 



 11

(3)

where

thrsrL





(4)

In (3), the sign of L

is set positive when

ECG

> ECG

i+1

, and vice-versa.

The signal ECG in equation (2) is then replaced

by the modified signal ECG

corct

which contains the

adapted samples ECG

corct,i

and ECG

corct,i+1

. (2), (3),

and (4) are iteratively recalculated until L

≤ 0. The

decreasing value of r

calculated at each iteration

ensures the convergence of the parameter L

. After

the last iteration, all samples of ECG which have

slope larger than thrs are adapted within ECG

corct

and, therefore, match the samples of the QRS

complex.

3.3 QRS Detector for Methodology

Evaluation

The following QRS detector was implemented for

evaluation of our methodology, according to the

common algorithm structure proposed for QRS

detection (Köhler et al., 2002):

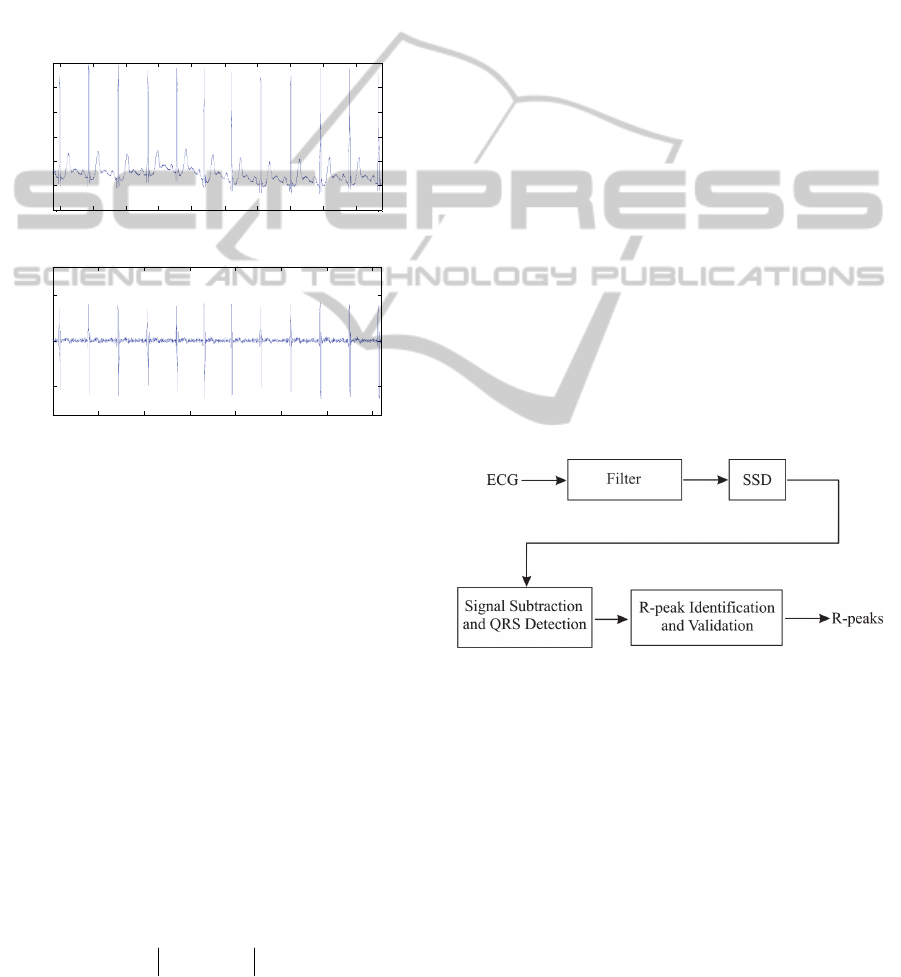
Figure 2: Block diagram structure of the QRS detector

algorithm for methodology evaluation.

As observed in the diagram above, a filter is

applied to the ECG signal before application of SSD.

As is done with most QRS detector algorithms, a

band-pass filter was used. This filter was set up as a

56-coefficient FIR, cut-off frequencies at 8 and

35 Hz. The reason to set the cut-off frequency at

35 Hz is because we noticed that a lower value

causes considerable attenuation of the amplitude of

QRS samples. This fact is in agreement with Thakor

et al. (1984) which indicate that the bandwidth of the

QRS complex ranges from 5 to around 40 Hz.

Application of the filter stage of figure 2 could

be bypassed when the ECG signal is affected by

DetectionofSharpWaveActivityinBiologicalSignalsusingDifferentiationbetweenConsecutiveSamples

329

artefacts whose signal slope has order of magnitude

much lower than the slope of the QRS samples, as

discussed below.

3.4 Signal Subtraction and QRS

Detection

As depicted in figure 2, after SSD approach

described by (1) – (4) to be employed for adapting

the samples associated to the QRS complex, a

further subtraction stage is carried out for QRS

samples selection, as follows:

corctfilt

ECGECGP 

sig

(5)

where P

sig

contains the QRS selected samples.

ECG

filt

and ECG

corct

correspond to the ECG signal

after filtering and SSD application respectively. As

SSD approach adapts samples with larger signal

slopes associated to the QRS complex, the

subtraction indicated in (5) excludes other regions of

the ECG signal in such a way that the latter are

represented as zero values within P

sig

. Therefore, the

samples of P

sig

whose value is different from zero

are assumed to belong to the QRS complex.

3.5 R-peak Identification and

Validation

Motion artefacts and drifting baselines are corrected

during the subtraction performed in (5). Hence, the

filtering stage shown in figure 2 could be used only

when the signal is affected by artefacts whose signal

slope is higher than thrs. Otherwise, there is no need

for calculating another threshold for identification of

the R-peaks as well. In this situation, since the

samples of P

sig

could be grouped in clusters

corresponding to each QRS complex, the maximum

sample amplitude of each cluster corresponds to the

respective R-peak.

On the other hand, R-peak validation rules are

demanded when the noise sample slope is higher

than thrs, and calculation of a second threshold is

also necessary. We tested a second threshold, trp,

calculated taking into account the RMS value of the

samples that belong to clusters corresponding to the

last QRS complexes located. trp was set as being

50% of such a RMS value.

Also for peak validation, the minimum time

between two consecutive clusters was set as 200 ms,

considering the ECG refractory period. Thus, when

two consecutive clusters along P

sig

had a time

difference lower than 200 ms, they were grouped

into a unique cluster whose maximum sample

amplitude was validated as identified R-peak.

3.6 QRS Detection Performance

Analysis

According to Köhler et al. (2002), the usage of

software QRS detection algorithms requires the

evaluation of the detection performance. In this way,

ANSI/AAMI/ISO EC57 (1998) recommends that the

parameters sensitivity (Se) and positive predictivity

(+P) should be calculated for algorithm assessment:

FNTP





(6)

FPTP





(7)

where TP is the number of true positives, FN the

number of false negatives, and FP is the number of

false positive QRS predictions.

4 RESULTS

Figure 3 illustrates the application of our

methodology in the ECG excerpt of figure 1a.

For the signal shown in figure 3a, the band-pass

filter was not applied in order to illustrate the

application of our methodology to a raw ECG signal

with high SNR. As observed in figure 3b, SSD

approach adapts only ECG samples associated to the

sharp wave activity of the QRS complexes whose

slope is higher than thrs. Figure 4 depicts a zooming

in around the time 811.5 s showing the samples

identified as QRS samples.

Evaluation of our methodology was performed

by application of the QRS detector of figure 2 to the

recordings of the MIT-BH Noise Stress Test

Database in accordance with ANSI/AAMI/ISO

EC57 (1998). This database corresponds to twelve

30 min ECG recordings with different levels of SNR

at 0, 6, 12, 18, 24, and -6 dB.

The results obtained for the parameters Se and

+P are presented in table 1. The QRS detector

shows high sensitivity (above 84%) even when the

SNR is about -6 dB. Although the values obtained

for +P are affected by a larger number of false

positives which occur under low SNR conditions,

the noise tolerance performance of such a detector is

comparable to other ones proposed in the literature

(Benitez et al., 2000); (Rezk et al., 2011).

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

330

808 809 810 811 812 813 814 815 816 817

-1

ECG signal

Signal (



Time(s)

808 809 810 811 812 813 814 815 816 817

-1

ECG signal after application of SSD

Signal (



Time(s)

808 809 810 811 812 813 814 815 816 817

0.5

1.5

ECG signal after subtraction stage

Signal

(



Time(s)

Figure 3: (a) ECG signal of figure 1a; (b) ECG

corct

resulting from application of SSD to (a); (c) P

sig

absolute value of the subtraction between (a) and (b).

810 810.5 811 811.5 812 812.5 813

-1

-0.5

0.5

1.5

Identified QRS samples

Signal (



Time(s)

Figure 4: Zooming in figure 3a, around time 811.5 s. The

regions of sharp wave activity with signal slope higher

than thrs are identified as QRS samples (thick blue traces).

Table 1: Se and +P calculated for the MIT-BH Noise

Stress Test Database considering application of the QRS

detector depicted in figure 2.

Recording

Se (%) +P (%)

118e00 91.62 79.33

118e06 98.24 86.24

118e12 99.96 93.47

118e18 99.96 98.91

118e24 99.96 99.56

118e_6 84.11 74.64

119e00 95.36 82.04

119e06 99.09 87.77

119e12 99.90 97.45

119e18 100 100

119e24 100 100

119e_6 85.51 71.96

5 DISCUSSION

As observed in figure 1, the difference between

consecutive samples of the ECG signal can be used

for identification of the shaper wave activity

associated to QRS complex (Rangayyan, 2002). This

property can be also observed in other biological

signals or under specific conditions where the signal

is affected by artefacts or other types of interference,

as discussed by Cluitmans et al. (1993), Van de

Velde et al. (1998), and Ferreira et al. (2012).

Ferreira et al. propose a methodology for

detection and removal of gradient artefact residuals

which also identifies artefact samples by the

magnitude of the signal slope. Thus, we developed a

modification of such a method for identification and

selection of signal samples which contain sharp

wave activity, described by equations (1) – (4).

When applied to the ECG signal, these equations

results in an effective identification of the QRS

samples, as depicted in figures 3 and 4.

Application of our methodology within the

prototype of QRS detector (figure 2) reveals that it

has a good performance for identifying the R-peaks,

even under conditions of low SNR (table 1).

According to Arzeno et al. (2008), first-derivative-

based methods can be easily implemented in real-

time R-peak detection. Such advantage is also

observed for the detector of figure 2. Moreover, it

shows to be effective for detection of ectopic beats

as well. Hence, in future work the performance of

this QRS detector will be evaluated for a larger set

of data and during removal of the ballistogram

artefact as well, according to the approach proposed

by Allen et al. (1998).

Therefore, the results shown in figures 3 and 4,

and table 1 reflect the effectiveness of SSD in the

detection of the steep wave activity of the QRS

complex. This fact clearly indicates the possibility to

apply the same approach to detect regions or

artefacts in other biological signals which possess

similar behaviour of the slope parameter.

Identification of samples as belonging to the sharp

wave activity region of interest depends on the value

of the slope signal threshold, estimated by equation

(1) for the ECG signal. Thus, our methodology

achieves better performance when the slope of the

sharp wave activity samples is higher and does not

overlap the slope magnitude of other regions of the

analysed signal.

Another fact which should be investigated in

future work is how the application of SSD approach

could be used to identify samples from a specific

frequency bandwidth in the biological signal. For

DetectionofSharpWaveActivityinBiologicalSignalsusingDifferentiationbetweenConsecutiveSamples

331

example, in the case of the QRS complex region,

this bandwidth ranges from around 5 to 40 Hz. In

experiments which involve removal of gradient

artefacts residuals from EEG signals, SSD shows to

select higher frequency components associated to

the artefact (Ritter et al., 2010; Ferreira et al. 2012).

Thereby, SSD could be evaluated and proposed as

an alternative time-domain filtering approach.

6 CONCLUSIONS

In this work, we propose a methodology (SSD) for

detection of sharp wave activity in biological signals

based upon differentiation of consecutive samples of

the digital signal.

Our methodology shows to achieve effective

identification of the sharp wave activity associated

to the QRS samples in the ECG signal. Also

evaluation of a QRS detector prototype which makes

use of SSD reveals that the QRS complexes are

localized with sensitivity and positive predictivity

comparable to other methodologies proposed in the

literature. In future work, our methodology shall be

applied and evaluated for detection of sharp wave

activity in other types of biological signals.

ACKNOWLEDGEMENTS

This work has been made possible by a grant from

the European Union and Erasmus Mundus – EBW II

Project, and by a grant from CNPq – Science

without Borders Program.

REFERENCES

Allen, P., Polizzi, G., Krakow, K., Fish, D., Lemieux, L.,

1998. Identification of EEG events in the MR scanner:

the problem of pulse artefact and a method for its

subtraction. NeuroImage. 8, 229-239.

ANSI/AAMI/ISO EC57, 1998. Testing and reporting

performance results of cardiac rhythm and ST segment

measurement algorithms. AAMI Recommended

Practice/ American National Standard.

Arzeno, N., Deng, Z., Poon, C., 2008. Analysis of first-

derivative based QRS detection algorithms. IEEE

Trans. Biomed. Eng. 55 (2), 478-484.

Benitez, D., Gaydecki, P., Zaidi, A., Fitzpatrick, A., 2000.

A new QRS detection algorithm based on the Hilbert

transform. Comput. Cardiol. 27, 379-382.

Clifford, G., 2006. ECG statistics, noise, artifacts, and

missing data. In G. Clifford, F. Azuaje, P. McSharry,

(eds.), Advanced tools for ECG data analysis. Artech

House: Boston, London.

Cluitmans, P., Jansen, J., Beneken, J., 1993. Artefact

detection and removal during auditory evoked

potential monitoring. J. Clin. Monit. 9 (2), 112–120.

Ferreira, J., Cluitmans, P., Aarts, R. M., 2012. Gradient

artefact correction in the EEG signal recorded within

the fMRI scanner. Proceedings of the 5

International

Conference on Bio-inspired Systems and Signal

Processing, BIOSIGNALS 2012, Vilamoura, Portugal,

February 1 – 4, 2012. 110-117.

Hamilton, P., Tompkins, W., 1986. Quantitative

investigation of QRS detection rules using the

MIT/BIH Arrhythmia Database. IEEE Trans. Biomed.

Eng. 33 (12), 1157-1165.

Köhler, B., Hennig, C., Orglmeister, R., 2002. The

principles of software QRS detection. IEEE Eng. Med.

Biol. Mag. 21 (1), 42-57.

MIT-BIH, 1998. Database Distribution. Massachusetts

Institute of Technology, Cambridge, MA. Available:

http://ecg.mit.edu/.

Pan, J., Tompkins, W., 1985. A real-time QRS detection

algorithm. IEEE Trans. Biomed. Eng. 32 (3), 230-236.

Rangayyan, R., 2002. Biomedical signal analysis: a case-

study approach. Wiley: New York.

Rezk, S., Join, C., Asmi, S., 2011. An algebraic

derivative-based method for R wave detection.

Proceedings of the 19

European Signal Processing

Conference, EUSIPCO 2011, Barcelona, Spain,

August 29 – September 2, 2011. 1578-1582.

Ritter, P., Becker, R., Freyer, F., Villringer, A., 2010. EEG

quality: the image acquisition artifact. In C. Mulert, L.

Limieux (eds.), EEG-fMRI: Physiological basis,

technique and applications. Springer: Verlag, Berlin,

Heidelberg.

Thakor, N., Webster, J., Tompkins, W., 1984. Estimation

of QRS complex power spectra for design a QRS

filter. IEEE Trans. Biomed. Eng. 31 (11), 702-706.

Van de Velde, R., Van Erp, G., Cluitmans, P., 1998.

Detection of muscle artefact in the normal human

awake EEG. Electroencephalogr. Clin. Neurophysiol.

107, 149-158.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

332