Exploratory EEG Analysis using Clustering and Phase-locking Factor

Carlos Carreiras, Helena Aidos, Hugo Silva and Ana Fred

Instituto de Telecomunicac¸˜oes, Instituto Superior T´ecnico, Lisbon, Portugal

Keywords:

Emotions, EEG, ICA, EMD, Phase-locking Factor, Clustering.

Abstract:

Emotion recognition is essential for psychological and psychiatric applications and for improving the quality

of human-machine interaction. Therefore, a simple and reliable method is needed to automatically assess the

emotional state of a subject. This paper presents an application of clustering algorithms to feature spaces

obtained from the acquired EEG of subjects performing a stress-inducing task. These features were obtained

in three ways: using the EEG directly, using ICA to remove eye movement artifacts, and using EMD to extract

data-driven modes present in the signals. From these features, we computed band-power features (BPFs) as

well as pairwise phase-locking factors (PLFs), in a total of six different feature spaces. These six feature

spaces are used as input to various clustering algorithms. The results of these clustering techniques show

interesting phenomena, including prevalence for low numbers of clusters and the fact that clusters tend to be

made of consecutive test lines.

1 INTRODUCTION

Emotions play a pivotal role in human communica-

tion, sometimes even more important than the actual

ideas being transmitted. For instance, imagine your-

self vacationing in a foreign country, not understand-

ing the local language. Naturally, there is a gaping

language barrier in any communication attempt. Nev-

ertheless, you can easily and intuitively gage the emo-

tional state of your interlocutor, knowing if s/he is be-

ing aggressive, pleasant, sad, happy, etc., allowing to

infer, in rough terms, what is going on. Indeed, the

need to communicate emotion has inspired the devel-

opment of the famous emoticons for text-based Inter-

net chatting, though the participants may not always

be truthful (Herbert, 2012).

However, this aspect of communication is lacking

in human-machine interaction, where the machines

(e.g. your personal computer) cannot understand nor

produce emotional cues, which could potentially aug-

ment the interaction quality. Therefore, there is a need

to, by simple and reliable means, assess the emo-

tional state of a person, not only in the context of

human-machine interaction, but also in psychologi-

cal and psychiatric studies, which many times rely

on self-evaluation questionnaires to assess the emo-

tions elicited during the experiments (Coan and Allen,

2007).

One possible approach to automatic emotion reco-

gnition is by analyzing the subject’s biosignals (e.g.

electrodermal activity, blood-volume-pulse, periph-

eral temperature, electrocardiogram signals) during

emotion elicitation (Canento et al., 2011). In partic-

ular, the electroencephalogram (EEG) is a noninva-

sive, cost effective and simple technique, with good

temporal resolution (Mak and Wolpaw, 2009), pro-

viding a measure of what is happening in the brain,

the physiological source of emotions. It has long been

noted that the EEG can provide information about the

emotional state of the subject, in particular regard-

ing frontal asymmetries (Ahern and Schwartz, 1985;

Coan and Allen, 2004). In this paper, we make an ex-

ploratory analysis of the EEG acquired from subjects

performing a stressful task, demanding high concen-

tration levels over a long period of time. This exper-

iment mimics what may happen during an interactive

educational game, where it would be useful to de-

tect when the subject is growing tired of performing a

certain task, seamlessly switching to another, less de-

manding activity.

Traditionally, EEG signals are analyzed by ex-

tracting band power features, given that brain ac-

tivity, as measured from the scalp, exhibits an os-

cillatory behavior whose dynamics (amplitude, fre-

quency and phase) are modulated by the various neu-

rological tasks (Pfurtscheller and Lopes da Silva,

1999). For example, the task of movement prepa-

ration induces a decrease of the EEG power in the

Carreiras C., Aidos H., Silva H. and Fred A..

Exploratory EEG Analysis using Clustering and Phase-locking Factor.

DOI: 10.5220/0004251300790088

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2013), pages 79-88

ISBN: 978-989-8565-36-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

motor cortex, termed Event-Related Desynchroniza-

tion (Pfurtscheller and Lopes da Silva, 1999). How-

ever, band power features require the selection of the

frequency bands, which may change from subject to

subject. An alternative method to analyze the EEG,

the Phase-Locking Factor (PLF), has been proposed

in the ﬁeld of Brain-Computer Interfaces (Carreiras

et al., 2012), which we apply here in the context of

emotion analysis. This measure may be useful in the

sense that, as a synchronization measure, it can iden-

tify the previously mentioned frontal asymmetries ob-

served in the EEG.

This paper is organized as follows: Section 2 de-

scribes the process used to obtain the EEG signals.

Section 3 details the methodology proposed in this

paper,which consists of three main stages: signal pro-

cessing (section 3.1), feature extraction (section 3.2)

and clustering (section 3.3). Section 4 presents the re-

sults obtained after applying this methodology to the

EEG data. Section 5 and section 6 discuss these ﬁnd-

ings and present concluding remarks, respectively.

2 EMOTION ELICITATION AND

DATA ACQUISITION

The EEG signals were obtained in the context of

the HiMotion project (Gamboa et al., 2007), an ex-

periment to acquire information related to human-

computer interaction and physiological signals on dif-

ferent cognitive activities. The signals were acquired

at four scalp locations according to the 10-20 system

, F

, and O

– see Figure 1), with a sampling

frequency of 256 Hz.

Figure 1: Location of the acquired electrodes (red).

During the acquisition, the subjects were asked to

perform various interactive cognitive tasks. In partic-

ular, a concentration task was performed, inspired in a

test from the MENSA set (Fulton, 2000). In this test,

the subject is given a matrix (20 lines by 40 columns)

of integers. The goal is to identify, line by line, pairs

of consecutive numbers that add to 10 (see Figure 2).

This task is cognitively demanding, as the pairs can

be consecutive (i.e. the same number can be used in

more than one pair), and therefore the test measures

the capability of the subject to maintain concentra-

tion over a long period of time, being expected to be

stress-inducing. EEG data was recorded from 24 sub-

jects (17 males and 7 females) with ages in the range

23.3±2.4 years.

Figure 2: Example matrix of the concentration test; the user

selects, line by line, the pairs of consecutive numbers that

add to 10.

3 THE PROPOSED

METHODOLOGY

In order to analyze the EEG signals obtained as de-

scribed in section 2, we propose the methodologypre-

sented in ﬁgure 3. This methodology starts with a ﬁl-

tering stage, following by a denoising process using

independent component analysis (ICA) and empiri-

cal mode decomposition (EMD). The EEG features

are obtained in the feature extraction stage using two

different measures: band-power features (BPF) and

phase-locking factor (PLF). Finally, several cluster-

ing algorithms are applied to each of the six feature

spaces and the results are analyzed to detect changes

in the emotional state. All these stages are explained

in detail in the following subsections.

3.1 Signal Processing

In order to eliminate noise from non-biological

sources (power-line noise, baseline wander, etc.), the

raw EEG was processed with two Butterworth ﬁlters,

applied with both a forward and a backward pass, to

avoid phase disruptions: one high-pass ﬁlter, order 8,

with cutoff frequency at 4 Hz and one low-pass ﬁl-

ter, order 16, with cutoff frequency at 40 Hz. How-

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

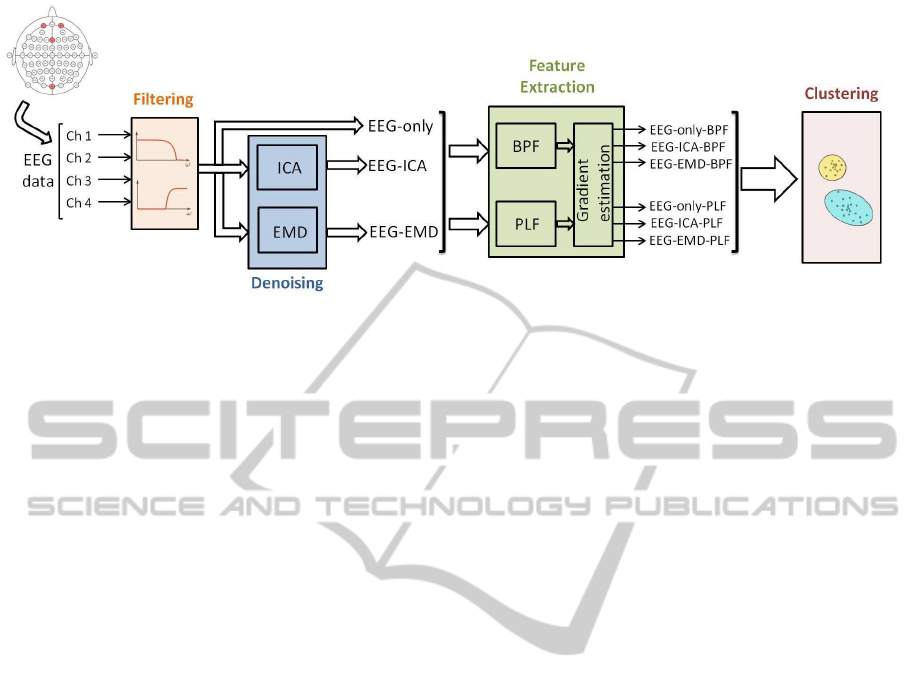
Figure 3: Scheme with the proposed methodology.

ever, the resulting signal is still fraught with biologi-

cal artifacts, such as eye blinks, eye movements, and

other muscle contractions. Therefore, three distinct

paths were evaluated to later apply the feature extrac-

tion algorithms. The ﬁrst, and simplest approach ap-

plies no further noise reduction, which we will call as

the EEG-only approach, based on the ﬁltered EEG.

The second approach uses Independent Component

Analysis (ICA) in an attempt to reduce the impact

of eye artifacts (denoted as EEG-ICA). Finally, the

last solution employs Empirical Mode Decomposition

(EMD), a method to analyze nonstationary and non-

linear data (denoted as EEG-EMD).

3.1.1 Independent Component Analysis

In the blind source separation problem (BSS), let X =

, ..., X

]

(M being the number of signals) be the

observed data produced by a linear mixture of some

source signals S = [S

, ..., S

]

(N being the number

of sources), deﬁned by the M ×N matrix A:

X = AS. (1)

The crux of the BSS problem is how to estimate

the sources S and the mixing matrix A from the ob-

served signals X. One of the available methods to do

so is Independent Component Analysis (ICA). The

ICA method estimates the sources by optimizing a

measure of their independence, resulting in sources

that are maximally independent (Hyv¨arinen et al.,

2001).

It has been shown that the ICA method is effec-

tive at separating neural activity from muscle and

blink artifacts in EEG data (Jung et al., 2000). In

this paper, we use the ubiquitous FastICA algorithm

(Hyv¨arinen, 1999) to decomposethe ﬁltered EEG into

its independent components, although other alterna-

tives are available in the literature, such as the EFICA

(Koldovsky et al., 2006) or Extended Infomax (Lee

et al., 2006) algorithms. We then visually identi-

ﬁed and eliminated the component that best isolated

the eye artifacts, reconstructing the EEG without that

component. Note that, as the acquired EEG signals

only have four channels, we chose to remove just

one of the components. An example of the original

EEG signal, its ICA decomposition and reconstruc-

tion without the noisy component can be seen in Fig-

ure 4.

3.1.2 Empirical Mode Decomposition

The Empirical Mode Decomposition algorithm de-

composes a given signal into a series of Intrin-

sic Mode Function (IMFs), using a sifting process

(Huang et al., 1998). This data-driven method pro-

duces components whose number of extrema differs

from the number of zero crossings, at most, by one,

and, additionally, at any point, the local mean is zero

(in an envelope deﬁned by the local maxima and min-

ima). The sum of the IMFs approximates the original

signal, thus guaranteeingcompleteness of the method.

Each IMF is associated with the intrinsic time scales

of the signal, from ﬁne temporal scales (high fre-

quency modes) to coarse temporal scales (low fre-

quency modes).

In this paper, each EEG signal was decomposed

with the EMD method, selecting the IMFs with mean

energy above 5% of the maximum energy. The result-

ing components were treated as EEG-like signals for

the subsequent processing steps.

3.2 Feature Extraction

The EEG features extracted in this paper arise from

two different approaches to evaluate mental activity.

The ﬁrst approach uses the traditional band power fea-

tures (BPF), by computing the average power in a se-

ries of appropriate frequency bands (Section 3.2.1).

ExploratoryEEGAnalysisusingClusteringandPhase-lockingFactor

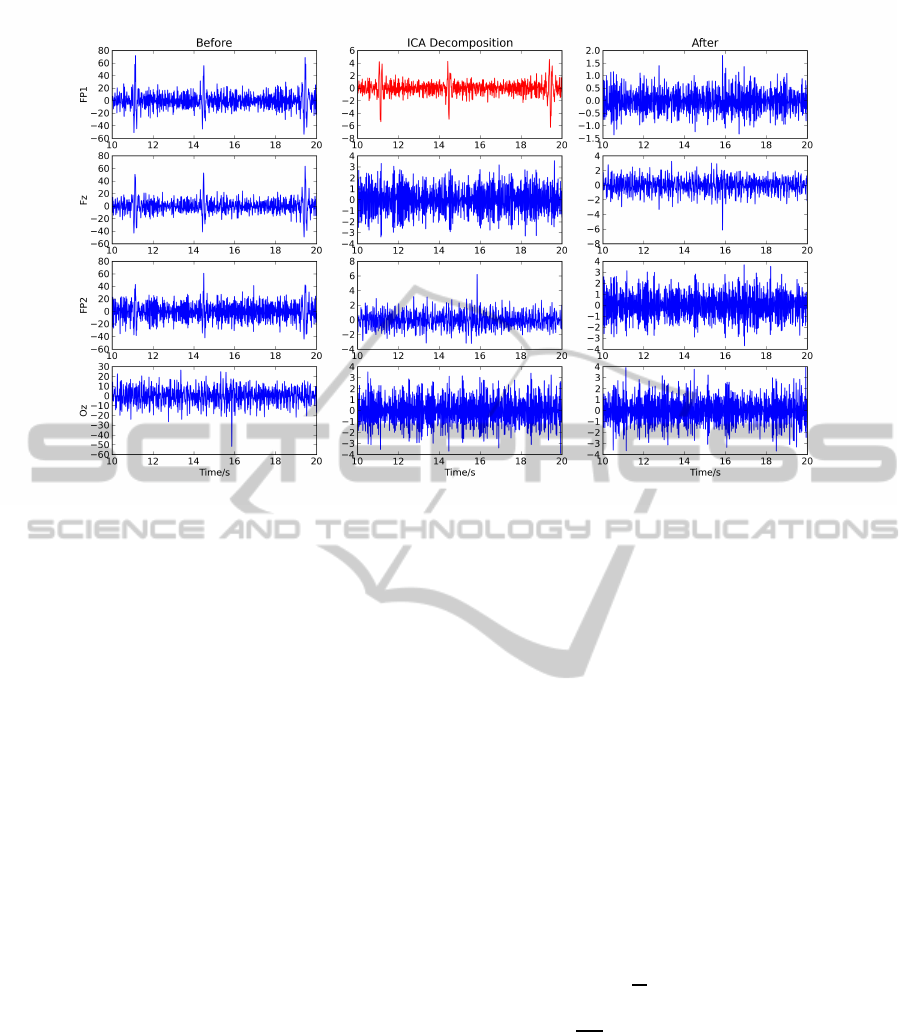
Figure 4: Example of applying the ICA method to remove eye artifacts from the EEG; the left column shows the four

original EEG channels, where the spikes are the eye artifacts; the middle column shows the ICA decomposition, with removed

component in red; and the right column presents the reconstructed EEG.

The second approach uses a method of synchroniza-

tion quantiﬁcation, the Phase-Locking Factor (PLF –

Section 3.2.2). However, one of the difﬁculties of an-

alyzing the biosignals resulting from a continuously

interactive experiment, such as presented here, is the

fact that different subjects will conclude the task in

different time intervals. In this particular case, there

is variability in the time a subject takes to conclude

each line of the Concentration test, and, consequently,

in the total length of the task. Therefore, a method

based on a Gradient Estimation was used to evaluate

the trend of both types of features (BPF and PLF) over

time, obtaining a value for each line of the concentra-

tion test (Section 3.2.3).

Note that each of the preprocessing alternatives

(EEG-only, EEG-ICA and EEG-EMD) was analyzed

with both kinds of feature extraction (BPF and PLF),

resulting in 6 different sets of features. For clarity, we

denote each set by the combination of the preprocess-

ing name and the feature extraction method. For in-

stance, the feature set “EEG-ICA-PLF” was obtained

by extracting the PLF features from the EEG prepro-

cessed by the ICA method.

3.2.1 Band Power Features

For the Band Power Features, the following bands

were considered:

• Theta Band: from 4 Hz to 8 Hz;

• Lower Alpha Band: from 8 Hz to 10 Hz;

• Upper Alpha Band: from 10 Hz to 13 Hz;

• Beta Band: from 13 Hz to 25 Hz;

• Gamma Band: from 25 Hz to 40 Hz.

The features were extracted, for each channel, by

computing a short-time Fourier transform in windows

of 500 ms, with 50% overlap, padding the windowed

signal with zeros up to 1024 samples. An order 5

median ﬁlter was then applied to the resulting time-

courses.

3.2.2 Phase-locking Factor

Given two oscillators with phases φ

[n] and φ

[n], n =

1, ..., T (with T the number of discrete time samples),

the PLF is deﬁned as (Almeida et al., 2011):



∑

n=1

j(φ

[n]−φ

[n])



, (2)

where j =

√

−1 is the imaginary unit. This measure

ranges from 0 to 1. While the value ρ

= 1 corre-

sponds to perfect synchronization between the two

signals (constant phase lag), the value ρ

= 0 cor-

responds to no synchronization. Put simply, the PLF

assesses whether the difference between the phases

of the oscillators are strongly or weakly clustered

around some angle in the complex unitary circle. In

this work, the phase information is extracted from the

EEG signals through the concept of analytical signals,

which is done by applying the Hilbert transform to the

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

signal. Given a real signal x(t), its Hilbert transform

is deﬁned as H

{x} = x(t) ∗

πt

, where ∗ denotes the

convolution operator; then, the corresponding analyt-

ical signal z(t) is obtained as:

z(t) = x(t) + jH

{x} = x(t) + j



x(t) ∗

πt



. (3)

The PLF was computed, for all possible electrode

pairs, in windows of 250 ms, with 50% overlap. An

order 5 median ﬁlter was then applied.

3.2.3 Gradient Estimation

In order to estimate the trend, over time, of the feature

sets, a straight line was ﬁtted to each line k = 1, ..., 20

of the concentration task (with T(k) duration), esti-

mating the gradient G(k) of that line. The evolution

of the features, from the initial state, over the lines is

then given by D(k):

D(k) = D(k −1) + G(k) ×T(k) (4)

with D(0) = 0. With this methodology we obtain,

for each line of the concentration task, a feature vec-

tor that characterizes that line. The dimension of the

feature vector depends both on the type of denois-

ing (EEG-only, ICA, EMD) and the feature extrac-

tion method (BPF, PLF). Denoting as C the number

of channels at the output of the denoising step, the

BPF method produces 5 ×C features per line (5 fre-

quency bands), while the PLF method produces





features (combinations of C choose 2, without repeti-

tions). The feature sets are then fed to the clustering

algorithms described in the following subsection.

3.3 Clustering Algorithms

Clustering consists in grouping objects that share

some characteristics. To identify which objects

should be grouped together, we need some similar-

ity measure such as the Euclidean distance. Cluster-

ing algorithms can be divided in two major categories:

hierarchical and partitional algorithms.

Hierarchical clustering algorithms output a tree

structure of nested objects, called dendrogram; one

can cut the dendrogram to obtain a partition of the

data. The level to cut the dendrogram can be de-

cided based on the lifetime of the clusters (Theodor-

idis and Koutroumbas, 2009); we use the largest life-

time criterion (Fred and Jain, 2002) in all of our ex-

periments. Examples of typical hierarchical algo-

rithms are single-link, average-link and ward-linkage

(Theodoridis and Koutroumbas, 2009).

Partitional clustering algorithms simply assign an

object to a single cluster. The simplest and most

widespread algorithm in this category is k-means

(Jain, 2010).

In this paper, we will apply various clustering

algorithms to the six feature spaces deﬁned in sec-

tion 3.2 (EEG-only-BPF, EEG-ICA-BPF, etc). We

apply average-link (AL) and ward-linkage (WL) to

those datasets; these two algorithmsdiffer in how they

measure the distance between two clusters. The AL

algorithm uses the average distance for all pairs of

points, one in one cluster and one in the other. It is

an algorithm that tends to merge clusters with small

variances and takes into account the cluster structure.

The WL algorithm is based on the increase in sum of

squares within clusters, after merging, summed over

all points. This algorithm tends to ﬁnd same-size,

spherical clusters and it is sensitive to outliers.

Recently, a single-link based algorithm has been

proposed using a dissimilarity measure based on

triplets of points, called dissimilarity increments, in-

stead of pairwise dissimilarities (Aidos and Fred,

2011). This algorithm uses the same principle for the

choice of clusters to merge as single-link; however,

the decision of merging two clusters or not is based

on the distribution of the dissimilarity increments. In

this paper, we will use average-link and ward-linkage

based algorithms following the same principle of dis-

similarity increments; we will call them ALDID and

WLDID.

Finally, we will also apply k-means to the signals,

with k set to 2 and 3.

4 EXPERIMENTAL RESULTS

4.1 Band Power Features

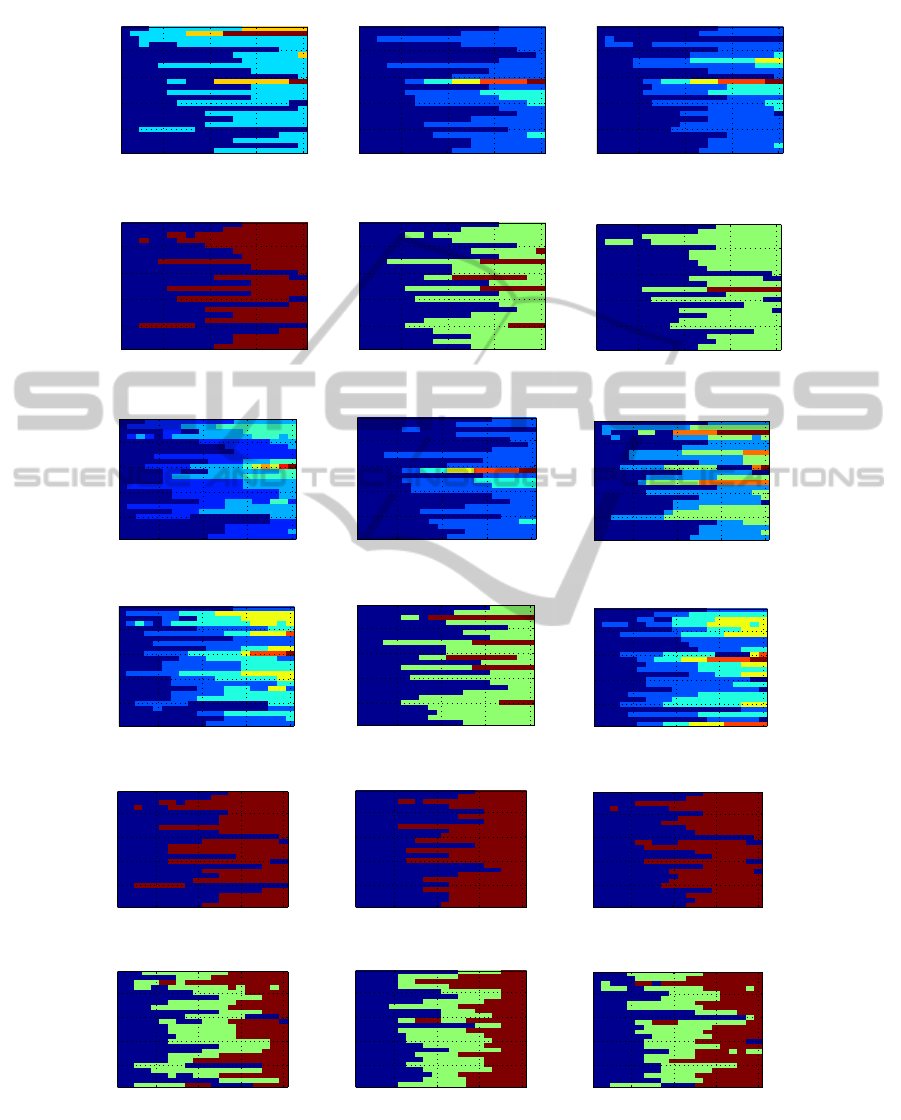
Figure 5 shows the results using the three BPF feature

spaces; different clusters are denoted using different

colors. There are a few major conclusions across all

subjects and clustering algorithms. In the vast major-

ity of cases, the lifetime criterion selects a lownumber

of clusters; usually 2 and sometimes 3, with 4 or more

clusters being very rare. Furthermore, again in the

majority of cases, each cluster consists of intervals of

test lines. For example, subject 24, when analyzed us-

ing EEG-only-BPF and AL (top-left subﬁgure in ﬁg-

ure 5), has the ﬁrst 10 test lines in one cluster and the

last 10 test lines in the other cluster. There are few

exceptions to this, such as subject 4 on the same sub-

ﬁgure (which has one cluster consisting of test lines 1,

2, 4, 5 and 6, which is not an interval because it does

not contain test line 3).

Since clusters usually correspond to intervals of

test lines, in the majority of cases it makes sense to

ExploratoryEEGAnalysisusingClusteringandPhase-lockingFactor

test line

subjects

EEG−only−BPF −− AL

5 10 15 20

test line

subjects

EEG−ICA−BPF −− AL

5 10 15 20

test line

subjects

EEG−EMD−BPF −− AL

5 10 15 20

test line

subjects

EEG−only−BPF −− WL

5 10 15 20

test line

subjects

EEG−ICA−BPF −− WL

5 10 15 20

test line

subjects

EEG−EMD−BPF −− WL

5 10 15 20

test line

subjects

EEG−only−BPF −− ALDID

5 10 15 20

test line

subjects

EEG−ICA−BPF −− ALDID

5 10 15 20

test line

subjects

EEG−EMD−BPF −− ALDID

5 10 15 20

test line

subjects

EEG−only−BPF −− WLDID

5 10 15 20

test line

subjects

EEG−ICA−BPF −− WLDID

5 10 15 20

test line

subjects

EEG−EMD−BPF −− WLDID

5 10 15 20

test line

subjects

EEG−only−BPF −− 2−means

5 10 15 20

test line

subjects

EEG−ICA−BPF −− 2−means

5 10 15 20

test line

subjects

EEG−EMD−BPF −− 2−means

5 10 15 20

test line

subjects

EEG−only−BPF −− 3−means

5 10 15 20

test line

subjects

EEG−ICA−BPF −− 3−means

5 10 15 20

test line

subjects

EEG−EMD−BPF −− 3−means

5 10 15 20

Figure 5: Clustering results for the EEG-BPF data. Each column corresponds to one type of data processing (from left

to right: EEG-only, ICA, EMD) and each row corresponds to one clustering algorithm (from top to bottom: average-link,

ward-linkage, ALDID, WLDID, 2-means and 3-means). In each subﬁgure, the horizontal axis spans the 20 test lines, and the

vertical axis spans the 24 subjects. Each different color denotes a different cluster.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

deﬁne transition test lines, which are the ﬁrst test line

of each interval of test lines in the same cluster, except

the initial test line. For example, for subject 24 using

EEG-only-BPF and AL, test line 11 is a transition test

line. A third global conclusion is that the transition

test lines tend to occur in the middle of the horizontal

axis, and less on the edges. The exceptions to this are

(EEG-only-BPF and ALDID), (EEG-only-BPF and

WLDID), (EEG-EMD-BPF and ALDID) and (EEG-

EMD-BPF and WLDID).

These transition test lines may correspond to sev-

eral things; for example, it might indicate a test line

where the subject began to feel more comfortablewith

the task, or it might indicate a time where the subject

began growing tired of maintaining high concentra-

tion levels. Further work, where subjects are queried

about their emotional state during the experiments, or

where test lines of different difﬁculties are used as a

proxy of stress level, is required to corroborate this

claim.

Still regarding ﬁgure 5, there are a few other in-

teresting conclusions. Subject 11 appears to be some-

what of an outlier: usually, all other subjects have 2-3

clusters, whereas subject 11 has many more (for ex-

ample, he/she has 6 on EEG-ICA-BPF using AL or

ALDID). This might suggest that something different

happened for this subject, such as improper experi-

mental setup or inability to understand the given in-

structions.

4.2 Phase-locking Factor

Figure 6 conveys the same information as ﬁgure 5,

but using the PLF features instead of the BPF ones.

Again, the majority of subjects yield clusters which

are composed of consecutivetime intervals. However,

and unlike ﬁgure 5, the number of clusters (and transi-

tions) is much smaller using the PLF features than us-

ing the BPF ones: the ICA features have a maximum

of 4 clusters on some subjects, and the EEG-only and

EMD ones have a maximum of 3.

There is a striking aspect in the EMD ﬁgures

(rightmost column): all cases have clusters made of

an interval, with no exceptions. Furthermore, in these

cases, there is never any transition in the ﬁrst 4 test

lines, nor on the last 2, and in the vast majority of

cases the transitions occur in the central part of the

ﬁgures (test lines 7 to 13 or so). This is markedly

different from the EEG-only cases (leftmost column)

where some subjects have non-interval clusters and

where transitions occur throughout the 20 test lines.

5 DISCUSSION

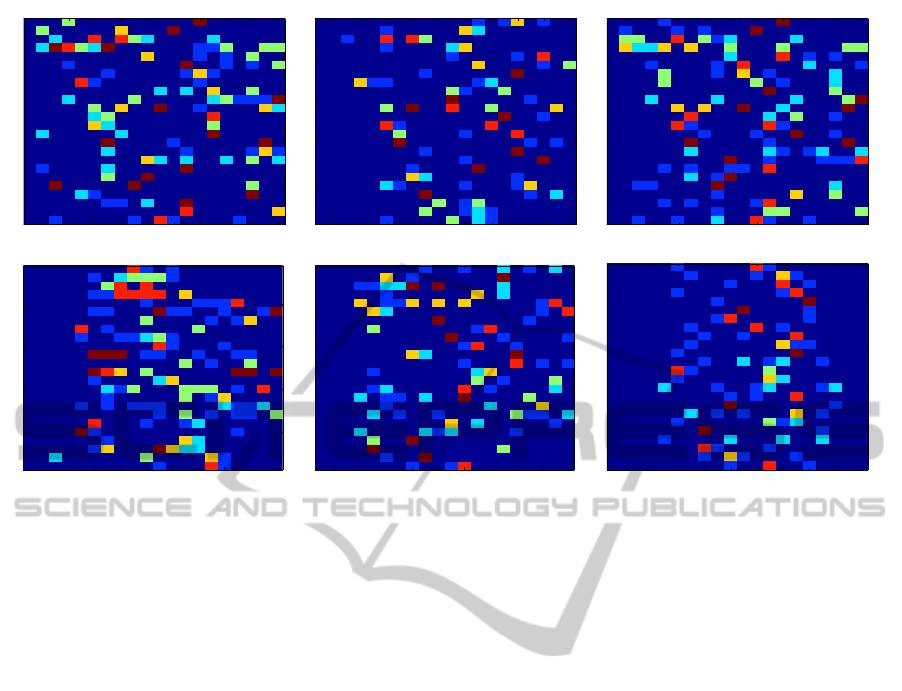
To further study the centrality of the transitions in the

EEG-EMD-PLF results, we computed the number of

algorithms which have a transition in test line t, for

each subject and each feature space. This is shown

in ﬁgure 7, where the horizontal and vertical axes are

similar to the previous ﬁgures, but now the color in-

dicates the number of algorithms where a transition

occurred in that test line for that subject. The values

range from 0 (no algorithms) to 6 (all algorithms). In

these plots, the centrality of the transitions for EEG-

EMD-PLF is clearly visible; it is also clear that the

other ﬁve feature spaces do not have this behavior.

This is an interesting ﬁnd which we plan to actively

investigate in the future, which may or may not be

related to the subject’s emotional state.

Another interesting ﬁnd for the EEG-EMD-PLF

case is that the vast majority of cases are either very

few transitions (0 or 1) or many transitions (5 or 6),

with few cases of intermediate numbers of transitions.

This indicates that the various clustering algorithms

agree with each other a lot more for the EEG-EMD-

PLF case than for all other cases. This agreement sug-

gests that some underlying (possibly emotional) phe-

nomenon is being captured by the use of EMD and

PLF which is missed otherwise.

6 CONCLUSIONS

We have presented a methodology for EEG ex-

ploratorydata analysis when subjects are asked to per-

form a task which requires high concentration lev-

els. We decomposed the data using simple band-

pass ﬁltering, independent component analysis (ICA)

and empirical mode decomposition (EMD). We then

computed two different measures: band-power fea-

tures (BPF), which measure the energyin typical EEG

bands, and phase-locking factors (PLF), which mea-

sure phase synchrony across pairs of channels. Clus-

tering, using various algorithms, was then applied to

these features.

We found interesting groups of test lines per sub-

ject, which may indicate moments when subjects be-

come more comfortable with the task they are re-

quired to do, or moments when it became hard to

maintain high concentration levels. The most inter-

esting combination of techniques was EMD and PLF,

which showed remarkable consistencyacross subjects

and clustering algorithms, detecting transitions ap-

proximately halfway through the set of test lines. Al-

though this study is still of limited scope, we can

conclude that an emotional and/or attentional factor

ExploratoryEEGAnalysisusingClusteringandPhase-lockingFactor

test line

subjects

EEG−only−PLF −− AL

5 10 15 20

test line

subjects

EEG−ICA−PLF −− AL

5 10 15 20

test line

subjects

EEG−EMD−PLF −− AL

5 10 15 20

test line

subjects

EEG−only−PLF −− WL

5 10 15 20

test line

subjects

EEG−ICA−PLF −− WL

5 10 15 20

test line

subjects

EEG−EMD−PLF −− WL

5 10 15 20

test line

subjects

EEG−only−PLF −− ALDID

5 10 15 20

test line

subjects

EEG−ICA−PLF −− ALDID

5 10 15 20

test line

subjects

EEG−EMD−PLF −− ALDID

5 10 15 20

test line

subjects

EEG−only−PLF −− WLDID

5 10 15 20

test line

subjects

EEG−ICA−PLF −− WLDID

5 10 15 20

test line

subjects

EEG−EMD−PLF −− WLDID

5 10 15 20

test line

subjects

EEG−only−PLF −− 2−means

5 10 15 20

test line

subjects

EEG−ICA−PLF −− 2−means

5 10 15 20

test line

subjects

EEG−EMD−PLF −− 2means

5 10 15 20

test line

subjects

EEG−only−PLF −− 3−means

5 10 15 20

test line

subjects

EEG−ICA−PLF −− 3−means

5 10 15 20

test line

subjects

EEG−EMD−PLF −− 3means

5 10 15 20

Figure 6: Clustering results for the EEG-PLF data. Each column corresponds to one type of data processing (from left to

right: EEG-only, ICA, EMD) and each row corresponds to one clustering algorithm (from top to bottom: average-link, ward-

linkage, ALDID, WLDID, 2-means and 3-means). In each subﬁgure, the horizontal axis spans the 20 test lines, and the

vertical axis spans the 24 subjects. Each different color denotes a different cluster.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

test line

subjects

EEG−only−BPF

2 4 6 8 10 12 14 16 18 20

test line

subjects

EEG−ICA−BPF

2 4 6 8 10 12 14 16 18 20

test line

subjects

EEG−EMD−BPF

2 4 6 8 10 12 14 16 18 20

test line

subjects

EEG−only−PLF

2 4 6 8 10 12 14 16 18 20

test line

subjects

EEG−ICA−PLF

2 4 6 8 10 12 14 16 18 20

test line

subjects

EEG−EMD−PLF

2 4 6 8 10 12 14 16 18 20

Figure 7: Number of transitions over all clustering algorithms per test line and per subject. The columns denote different data

processing methods (from left to right: EEG-only, ICA, EMD), as in the previous ﬁgures. The rows denote the two feature

spaces (top: BPF; bottom: PLF). In each subﬁgure, the horizontal axis spans the 20 test lines, and the vertical axis spans the

24 subjects. The color of each cell denotes the number of clustering algorithms which had a transition in that test line for that

subject.

changes in the EEG throughout the execution of the

concentration task.This motivates us to further inves-

tigate the recognition of emotional states from the

EEG using feature extraction measures such as the

PLF.

ACKNOWLEDGEMENTS

This work was supported by the Portuguese

Foundation for Science and Technology un-

der grants PTDC/EIA-CCO/103230/2008 and

SFRH/BD/65248/2009.

REFERENCES

Ahern, G. L. and Schwartz, G. E. (1985). Differential later-

alization for positive and negative emotion in the hu-

man brain: EEG spectral analysis. Neuropsychologia,

23:745–755.

Aidos, H. and Fred, A. (2011). Hierarchical clustering with

high order dissimilarities. In Proceedings of the 7th

International Conference on Machine Learning and

Data Mining (MLDM 2011), pages 280–293, New

York, USA.

Almeida, M., Schleimer, J.-H., Vigrio, R., and Bioucas-

Dias, J. (2011). Source separation and clustering of

phase-locked subspaces. IEEE Transactions on Neu-

ral Networks, 22:1419–1434.

Canento, F. and Fred, A. and Silva, H. and Gamboa, H. and

Lourenc¸o, A. (2011). Multimodal biosignal sensor

data handling for emotion recognition. In Proceed-

ings IEEE Sensors, pages 647–650.

Carreiras, C., de Almeida, L. B., and Sanches, J. M.

(2012). Phase-locking factor in a motor imagery

brain-computer interface. In Eng. in Medicine and

Biology Society, 2012. EMBS 2012. 34th Annual In-

ternational Conference of the IEEE.

Coan, J. A. and Allen, J. J. B. (2007). Handbook of emotion

elicitation and assessment. Oxford University Press.

Coan, J. A. and Allen, J. J. B. (2004). Frontal EEG asym-

metry as a moderator and mediator of emotion. Bio-

logical psychology, 67:7–50.

Fred, A. and Jain, A. K. (2002). Evidence Accumulation

Clustering based on the K-Means Algorithm. In ro-

ceedings of the 9th Joint IAPR International Work-

shop on Structural, Syntactic and Statistical Pattern

Recognition (SSPR 2002), pages 442–451, Windsor,

Canada.

Fulton, J. (2000). The Mensa Book of Total Genius. Carlton

Books.

Gamboa, H., Silva, H., and Fred, A. (2007). Himotion

project. Technical report, Instituto Superior Tcnico,

Lisbon, Portugal.

Herbert, W. (2012). How to Spot a Scoundrel. Scientiﬁc

American Mind, 23:70–71.

Huang, N., Shen, Z., Long, S., Wu, M., Shih, H., Zheng,

ExploratoryEEGAnalysisusingClusteringandPhase-lockingFactor

Q., Yen, N., Tung, C., and Liu, H. (1998). The em-

pirical mode decomposition and the hilbert spectrum

for nonlinear and non-stationary time series analysis.

Proceedings of the Royal Society of London. Series

A: Mathematical, Physical and Engineering Sciences,

454(1971):903–995.

Hyv¨arinen, A. (1999). Fast and robust ﬁxed-point algo-

rithms for independent component analysis. Neural

Networks, IEEE Transactions on, 10(3):626–634.

Hyv¨arinen, A., Karhunen, J., and Oja, E. (2001). In-

dependent component analysis, volume 26. Wiley-

interscience.

Jain, A. K. (2010). Data clustering: 50 years beyond k-

means. Pattern Recognition Letters, 31:651–666.

Jung, T., Makeig, S., Westerﬁeld, M., Townsend, J.,

Courchesne, E., and Sejnowski, T. (2000). Removal

of eye activity artifacts from visual event-related po-

tentials in normal and clinical subjects. Clinical Neu-

rophysiology, 111(10):1745–1758.

Koldovsky, Z. and Tichavsky, P. and Oja, E. (2006). Ef-

ﬁcient variant of algorithm FastICA for independent

component analysis attaining the Cram´er-Rao lower

bound. IEEE Transactions on Neural Networks,

17(5):1265–1277.

Lee, T. W. and Girolami, M. and Sejnowski, T. J. (1999).

Independent component analysis using an extended

infomax algorithm for mixed subgaussian and super-

gaussian sources. Neural computation, 11(2):417–

441.

Mak, J. N. and Wolpaw, J. R. (2009). Clinical Applica-

tions of Brain-Computer Interfaces: Current State and

Future Prospects. IEEE Reviews in Biomedical Engi-

neering, 2:187–199.

Pfurtscheller, G. and Lopes da Silva, F. H. (1999). Event-

related EEG/MEG synchronization and desynchro-

nization: basic principles. Clinical Neurophysiology,

110:1842 – 1857.

Theodoridis, S. and Koutroumbas, K. (2009). Pattern

Recognition. Elsevier Academic Press, 4th edition.

BIOSIGNALS2013-InternationalConferenceonBio-inspiredSystemsandSignalProcessing