
Mining Association Rules that Incorporate Transcription Factor
Binding Sites and Gene Expression Patterns in C. elegans
Hao Wan
1
, Gregory Barrett
1
, Carolina Ruiz
1
and Elizabeth F. Ryder
2
1
Department of Computer Science, Worcester Polytechnic Institute, Worcester, MA 01609, U.S.A.
2
Department of Biology & Biotechnology, Worcester Polytechnic Institute, Worcester, MA 01609, U.S.A.
Keywords: Gene Expression, C. elegans, Transcription Factor, Association Rule, Position Weight Matrix.
Abstract: Gene expression in different cells is regulated by different sets of transcription factors. How the
combinations of transcription factors required to achieve specificity of expression are encoded by regulatory
regions of DNA is a long-standing problem in biology. In the model system C. elegans, gene regulatory
regions are relatively compact, and much work has been done to describe gene expression patterns in a
number of cell types. In this work, we collected the promoter regions of genes with known expression
patterns in a limited number of neuronal cell types, and annotated any DNA motifs in the promoters that
corresponded to putative binding sites of known C. elegans transcription factors, using position weight
matrices. We used association rule mining to identify rules relating the presence of particular motifs with
expression of particular genes. We used metrics including confidence, support, lift, and p-value to mine and
assess rules. We examined the effect on the rules of multiple vs. single transcription factors, and the effect
of distance from transcription factor binding sites to the start of transcription. The mined association rules
were filtered by Benjamini and Hochberg’s approach, and the most interesting rules were selected. We also
validated our approach by generating association rules corresponding to gene expression patterns which
have been already revealed in biological research. We conclude that our system allows the identification of
interesting putative gene expression rules involving known transcription factors. These rules can be further
validated using biological techniques.
1 INTRODUCTION
There are numerous important research questions
related to gene expression. This paper deals with the
problem of finding relationships between
transcription factor binding sites (TFBSs) and cell
type-specific gene expression, using the nematode
worm C. elegans as a model system.
C. elegans has many advantages as a model
system for understanding gene regulation. Because
the genome is relatively compact, regulatory
sequences are often contained within relatively short
non-coding promoter regions, which are often close
to the regulated gene (The C. elegans Sequencing
Consortium, 1998). A number of groups have used
both computational and biological techniques to
elicit TFBSs and regulatory networks (Arda and
Walhout, 2010); (Bigelow et al., 2004); (Hobert et
al., 2010); (Ihuegbu et al., 2012); (Newburger and
Bulyk, 2009); (Reece-Hoyes et al., 2005). Much
information related to cell type specific gene
expression has been elucidated (Bamps and Hope,
2008); (Hunt-Newbury et al., 2007), and collected in
curated databases (Hope Laboratory Expression
Pattern Database); (WormBase). Studying cell type
specific regulation in the C. elegans nervous system
is particularly appealing, because the number of
neurons is small (302 in the adult hermaphrodite),
and all of the neurons are identified and classified
into 118 distinct types (Altun and Hall, 2011).
In previous work, we have developed an
association rule mining and visualization system,
and used a subset of C. elegans neurons with well-
defined gene expression patterns to try to identify,
using computational methods, new candidate TFBSs
from DNA motif sequences conserved among genes
expressed in the same cell type (Thakkar et al.,
2007). Here, we have used our system to focus on a
small number of experimentally validated, using
biological methods, transcription factor binding sites
in C. elegans. We asked the question whether we
could derive association rules using these binding
81
Wan H., Barrett G., Ruiz C. and F. Ryder E..
Mining Association Rules that Incorporate Transcription Factor Binding Sites and Gene Expression Patterns in C. elegans.
DOI: 10.5220/0004252300810089
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 81-89
ISBN: 978-989-8565-35-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

sites that would usefully describe and predict gene
regulatory patterns in neuron cell types in C.
elegans. We analyzed the combined effect of
multiple DNA motifs, and the effect of distance
between motifs and the start of transcription (SoT).
With correction for multiple tests using Benjamini
and Hochberg’s false discovery rate control method,
a number of significant association rules were
identified. These results suggest particular
combinations of transcription factors that may be
important in cell-specific expression in C. elegans.
The contributions of this paper include the
design and implementation of a new analysis
pipeline that starts with the collection of a new
dataset of C. elegans genes and biologically found
TFBSs. Gene promoter regions are annotated with
these TFBSs. Association rules that incorporate
presence and relative positions of these TFBSs in the
gene promoter regions, as well as gene expression
information, are mined. These rules are further
analyzed, refined, and statistically corrected for
multiple tests using our visualization and analysis
tools. Furthermore, association rules of potential
biological significance are singled out by this
analysis pipeline, and are postulated for further
biological analysis. In addition, this paper illustrates
how to use our computational tools to analyze and
refine rules obtained directly from biological
experiments.
2 BACKGROUND
2.1 Gene Expression
In C. elegans, a simplifying assumption is often
made that the promoter region a short distance
upstream from the start of translation is the only
sequence important in control of transcription
(Bamps and Hope, 2008). The start of translation is
used as if it were the start of transcription, because
the start of transcription can be difficult to determine
due to trans-splicing (Conrad et al., 1995). Where
the start of transcription is known, it is typically
close to the start of translation (The C. elegans
Sequencing Consortium, 1998); (WormBase). Large
scale studies have suggested that this assumption is
justified for a majority of assayed genes (Hunt-
Newbury et al., 2007); (Reece-Hoyes et al., 2007).
As a starting point for our work, we defined the
region 1000 bps upstream from the start of
translation as the promoter region.
The binding sites for a specific transcription
factor typically share a common nucleotide
sequence. Because the sequence is not completely
identical for each binding site, each TFBS is
represented as a Position Weight Matrix (PWM)
(Bailey, 1998). A PWM records the likelihood for
each nucleotide at each position of a TFBS. A motif
is a potential TFBS, which means that a motif is a
subsequence of DNA that is a reasonable match to
the transcription factor’s PWM.
2.2 Association Rules
Association rule mining (Agrawal et al., 1993) is a
technique to find frequently co-occurring items in
data. An association rule is a probabilistic rule of the
form: X→Y, where X and Y are sets of items in the
dataset. This rule means that Y is likely to occur in a
data instance when the data instance contains (or
satisfies) X. This likelihood is given by the
confidence of the rule (defined below). X is called
the antecedent and Y the consequent of the rule.
In this work, we use the ASAS (Pray and Ruiz,
2005) algorithm to mine the association rules of the
form:
,…,
,
,…,
→
where 1,0. This rule states that if a gene’s
promoter contains
,…,
and if their
locations satisfy
,…,
, the
gene is probably expressed in cell type C. The
conditions include the order of multiple motifs in the
gene’s promoter region, and the distance of the
motifs from SoT.
We used the following different metrics to assess
an association rule X→Y. Here,PA denotes the
proportion of data instances in the dataset that
contain or satisfy A.
Support(X→Y) =PX&Y.
Confidence(X→Y) = P
Y
|
X
&
.
Lift(X→Y) =
|
&
.
p-value(X→Y: A test statistic that measures the
likelihood that X and Y are independent (Alvarez,
2003).
Within-Cell-Support (X→Y) =
&
. This is not
a typical association rule metric, but a relevant
metric in our work. It provides the proportion of
genes in a cell type that share the pattern described
by the rule.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
82

Table 1: A small sample illustrating our dataset. The first sequence, named WBGene0001145, is expressed in cell type HSN
and contains two motifs; one might bind transcription factor HLH-1, and the other TRA-1. The first motif is 16 bps long
and occurs starting at 37 bps away from SoT.
Sequence HLH-1 TRA-1 DAF-16 … HLH-25 SKN-1 Cell types
WBGene0001145 [37:52] [236:258] [] … [] [] HSN
WBGene0000482 [] [] [569:582] … [547:562] [362:373] ADL, ALM, ASE, ASH, ASI
It is expected that rules with high confidence,
low p-value, high lift, and higher within–cell-type-
support would be more interesting and more likely
to show true relationships between transcription
factors and cell types.
2.3 Controlling False Discovery Rate
In our work, we use Benjamini’s and Hochberg’s
procedure to control Type I errors (Benjamini and
Hochberg, 1995). A Type I error occurs when a null
hypothesis is rejected even though it is true. The
more tests performed on a set of data, the more
likely a Type Ι error will occur. Consider tests
with null hypotheses
,
,…,
, and
corresponding p-values
,
,…,
. Let
⋯
. Benjamini’s and Hochberg’s procedure
works as follows: (1) Define a threshold , 0
1, to control the false discovery rate; (2) Let to be
the largest for which
/; (3) Reject all
null hypotheses
, 1,2,…,.
3 DATA COLLECTION AND
PREPROCESSING
All our data were collected from (WormBase). We
selected 11 neuron cell types from C. elegans: AIA,
AIY, ADL, ALM, ASE, ASH, ASI, ASK, CAN,
HSN, and PHA. This selection was based on each
cell type having at least 30 genes known to be
expressed in that cell type. We collected promoter
sequences of 331 unique genes expressed in these
cell types. We chose to limit the length for each
promoter sequence to 1000 bps. We used all 71
PWMs found in WormBase; these correspond to 52
different transcription factors.
We used MAST (Bailey, 1998) to annotate
potential binding sites of the transcription factors in
the gene promoter sequences. During this process,
the similarity between each pair of PWMs was
calculated. PWMs highly similar to others were
deleted, resulting in only 48 PWMs being kept. We
set the E-value threshold to 10. This MAST
parameter is a user required composite of the
strengths of all the motif matches found in a
sequence. By filtering the sequences with E-value
less than or equal to 10, 59 different promoter
sequences were kept. Finally, our dataset was
formed with these 59 promoter sequences annotated
with the aforementioned 48 PWMs, together with
information on which of the 11 cell types each gene
is expressed in. The annotation process resulted in a
maximum number of annotated PWMs in a promoter
sequence being equal to 17, a minimum number of
5, and an average of 11. In summary our dataset
consists of 59 data instances (gene promoters) and
59 attributes (48 corresponding to the annotated
motifs according to the 48 PWMs plus 11 cell
types). Table 1 shows a small sample of our dataset.
4 MINING OF PATTERNS
Our association rule mining algorithm takes as input
a dataset of instances of the type illustrated in Table
1; a minimum support threshold; and a minimum
confidence threshold. Its mining strategy is close in
spirit to that of the two-stage Apriori algorithm
(Agrawal and Srikant, 1994). That is, it first
constructs all candidate rules that satisfy the
minimum support threshold, and then keeps only
those rules that also satisfy the minimum confidence
threshold. However, our candidate rule generation is
more complex than that of the Apriori algorithm, as
it takes into account the positions of the annotated
motifs on the promoter regions of the genes relative
to one another, and relative to SoT. Handling the
added data complexity and the added expressiveness
of the rules requires the use of judicious prune
strategies and efficient data structures. Once that the
rules have been constructed based on the minimum
support and confidence thresholds, they are
annotated with their lift, p-value, and within-cell-
support. Table 2 contains examples of rules mined
by our algorithm.
In this work, we also use our interactive
visualization tool to visualize the dataset in the
context of a rule. This enables rule evaluation and
rule specialization according to biological
hypotheses regarding order, position, and spacing of
motifs.
MiningAssociationRulesthatIncorporateTranscriptionFactorBindingSitesandGeneExpressionPatternsinC.elegans
83
Based on these association rule mining and
visualization systems, we implemented the analysis
pipeline outlined below. Given a dataset D as
described in section 3 , a minimum
supportminsupp, and a minimum confidence
minconf:
1. Mine all association rules → of the form
described in section 2.2, with supportX → Y
minsupp, and confidence
X→Y
minconf.
2. Select the mined rules with p-value 0.05. We
then use these rules to generate new refined
association rules by applying the following
analysis methods:
a. Combined effect of Multiple Motifs Analysis:
for a rule with multiple motifs, we generate
new rules by deleting one motif in the original
rule at a time. We then compare the p-value of
the original rule with those of the generated
rules. This analysis is described in section 5.1.
b. Effect of Distance from SoT Analysis: we
refine an association rule by adding distance
constraints to it using our visualization tool.
We then compare the p-value in the original
rule with those of the refined rules. This
analysis is described in Section 5.2.
3. Apply the Benjamini and Hochberg’s correction
on each of two rule sets: one containing all the
mined rules (step 1 above); and the other one
containing all of the mined rules together with the
refined rules generated (steps 1 and 2 above). For
all the rules of one of the rule sets:
a. Sort the rules in an ascending order of p-values
…
:
,
,…,
.
b. Let to be the largest for which
,
where q=0.05.
c. Output the rules
,
,…,
.
5 RESULTS
For the results reported in this paper, a minimum
confidence of 0.2 and a minimum support of 0.1
were used, resulting in 51 mined association rules.
Among those rules, 15 had a p-value of less than
0.05; we call them significant rules. They are shown
in Table 2. We found 7 significant rules in which
there was more than one motif. These rules suggest
that two motifs work together in regulating gene
expression. The combined effect of motifs in each of
these rules will be analyzed in Section 5.1. We also
analyzed the effect of distance from SoT in the other
8 single-motif rules.
It is worth noting that typically in data mining, rules
that have high confidence are sought, with less
importance placed on support. However, given the
nature of gene expression data, the trade-off between
confidence and support needs to be re-evaluated. On
the one hand, high rule support is important in gene
expression analysis as we aim to find meaningful
patterns that apply to several genes. On the other
hand, low rule confidence may be observed because
there are numerous different (hidden) factors that
affect gene expression, and existing data do not
account for all of them. As a result, in this work we
use a lower threshold for rule confidence in order to
obtain rules that have greater support. Once rules
are mined, some of the hidden factors (e.g., the order
of the motifs, or their distance from each other, or
their distance from the SoT) may be identified by
visualizing the rules in the context of the dataset.
Those factors can then be used to refine the rules,
thereby increasing their confidence.
5.1 Combined Effect of Multiple Motifs
As shown in Table 3, we obtained 7 rules with two
motifs. We assessed whether the motifs in these
rules have a combined effect in gene expression, by
comparing the p-value of a rule with those of simple
rules created by keeping just one motif from the
original rule. For example, for the rule set 4 in Table
3: HNF-6 && HLH-4→HSN, the corresponding
simple rules are: HNF-6→HSN and HLH-4→HSN.
We expect the p-value of the multiple-motif rules to
be much better than those of the corresponding
single-motif rules if the motifs have a combined
effect on gene expression.
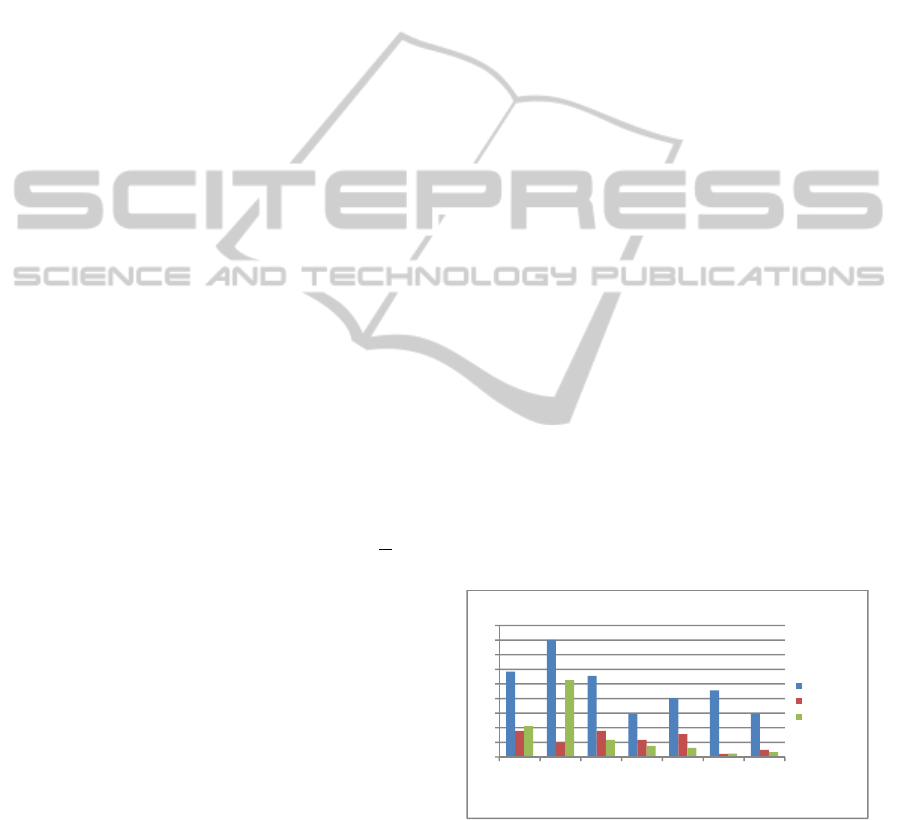
Figure 1: p-value comparison: multiple-motif vs. single-
motif rules. For each rule containing multiple motifs in
Table 2, we compared its p-value with those of the derived
rules containing only one motif, in order to determine
whether these motifs exhibit a combined effect.
0
2
4
6
8
10
12
14
16
18
Rule
set 1
Rule
set 2
Rule
set 4
Rule
set 8
Rule
set 9
Rule
set 10
Rule
set 13
Multiple
Simple 1
Simple 2
-log (p-value)
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
84

Table 2: Significant rules: these are the 15 mined rules with (uncorrected) p-value 0.05 obtained. The column Motif
contains motifs and conditions for each rule, and the column Cell Type has the cell type for each rule. Take the first rule as
an example: PHA-4 && CND-1[SoT] →ASE means that if both motifs CND-1 and PHA are found in a gene’s promoter
sequence, and CND-1 is closer to SoT, then there is a 100% confidence that the gene will be expressed in cell type ASE.
ID Motif Cell Type Confidence Support Lift p-value Within cell support
1 PHA-4&& CND-1[SoT] ASE 1.00 0.1017 2.95 3.07E-4 0.3 (6/20)
2 HLH-14&& HLH-19[SoT] PHA 0.86 0.1017 3.89 1.49E-5 0.46 (6/13)
3 PUF-11 ASE 0.67 0.1356 1.97 7.22E-3 0.4 (8/20)
4 HNF-6 && HLH-4[SoT] HSN 0.67 0.1017 3.03 4.49E-4 0.46 (6/13)
5 MEX ASE 0.58 0.1186 1.72 4.51E-2 0.35 (7/20)
6 HLH-19 PHA 0.58 0.1186 2.6 6.76E-4 0.54 (7/13)
7 PUF-11 PHA 0.50 0.1017 2.27 8.82E-3 0.46 (6/13)
8 MDL-1 && HLH-4 [SoT] HSN 0.40 0.1356 1.82 1.71E-2 0.62( 8/13)
9 PHA-4 && SIR-2[SoT] ASK 0.67 0.1017 2.46 3.74E-3 0.38 (6/16)
10 PHA-4 && HLH-4[SoT] CAN 0.55 0.1017 2.68 1.78E-3 0.5 (6/12)
11 LIN-32 CAN 0.50 0.1356 2.46 5.55E-4 0.67 (8/12)
12 PHA-4 ALM 0.50 0.1356 2.11 3.81E-3 0.57 (8/14)
13 MDL-1 && PHA-4 [SoT] ALM 0.50 0.1017 2.11 1.65E-2 0.43 (6/14)
14 PHA-4 ADL 0.46 0.1017 1.95 3.14E-2 0.43 (6/14)
15 PHA-4 AIY 0.22 0.1017 1.87 2.38E-2 0.86 (6/7)
Figure 1 shows –log(p-value) comparisons for all
the 7 rule sets. The larger this value, the better the
rule. In most of these rule sets, the measurement
value of the multiple-motif rule is much better than
the value of the simple rules. In rule set 4, for
example, the single rules are not even significant on
their own, while the joint one is highly significant.
Thus, these results provide some evidence that the
motifs in these rules have a combined effect on gene
expression. The details of the rules are in Table 3.
5.2 Effect of Distance from SoT
As mentioned in Section 1, it is believed that
distance between the motifs and SoT may affect
gene expression (MacIsaac et al., 2010). Thus, we
included distance as a factor in our association rules.
We checked if the rules could be improved by
adding distance from SoT constraints to them. This
rule refinement was performed using a visualization
tool we developed in prior work. Figure 3 shows an
example of a visualization of the rule PHA-
4→ALM. Note however that if we refine a rule by
only considering the motif’s location in a very
specific region, the p-value of the rule may improve
only at the expense of reducing the number of
sequences that support the refined rule. The resulting
rule might be meaningless because of its low
support. Thus, we aimed at keeping a balance
between getting a low p-value and keeping a high
support value. Distance refined rules are shown in
Table 4.
To compare the refined rules with the original
rules, we also used –log(p-value). For simplicity, in
this paper we only considered distance refinements
of rules with only one motif in their antecedents.
Figure 2 shows p-value comparisons of the 8 single-
motif rules in Table 2 with the distance refined rules
in Table 4. Except for Rule 11, the other rules were
improved by constraining the location of the motif in
each rule to a particular region of the promoter. This
illustrates how our visualization tool can aid in the
refinement of rules for future testing.
Figure 2: p-value comparison: Rules refined by distance
from SoT vs. original rules. To assess the effect of
distance from SoT in gene expression, we compared the p-
values of rules refined using distance constraints with
those of the corresponding original rules.
0
5
10
15
Rule
3
Rule
5
Rule
6
Rule
7
Rule
11
Rule
12
Rule
14
Rule
15
Original Rule
Refined Rule
‐log(p-value)
MiningAssociationRulesthatIncorporateTranscriptionFactorBindingSitesandGeneExpressionPatternsinC.elegans
85

Table 3: Multiple-motif rules and their corresponding single-motif rules.
ID Motif Cell Type Confidence Support Lift p-value
Within cell
support
1
PHA-4&& CND-1[SoT] ASE 1.00 0.10 2.95 3.07E-04 0.3
PHA-4 ASE 0.54 0.12 1.59 8.53E-02 0.35
CND-1 ASE 0.46 0.22 1.37 5.33E-02 0.65
2
HLH-14&& HLH-19[SoT] PHA 0.86 0.10 3.89 1.49E-05 0.46
HLH-14 PHA 0.25 0.20 1.13 2.51E-01 0.92
HLH-19 PHA 0.58 0.12 2.64 6.76E-04 0.54
4
HNF-6 && HLH-4[SoT] HSN 0.67 0.10 3.03 4.49E-04 0.46
HNF-6 HSN 0.35 0.12 1.59 8.53E-02 0.54
HLH-4 HSN 0.26 0.20 1.16 2.00E-01 0.92
8
MDL-1 && HLH-4 [SoT] HSN 0.40 0.14 1.82 1.71E-02 0.62
MDL-1 HSN 0.26 0.17 1.16 3.51E-01 0.77
HLH-4 HSN 0.26 0.20 1.16 2.00E-01 0.92
9
PHA-4 && SIR-2[SoT] ASK 0.67 0.10 2.46 3.74E-03 0.38
PHA-4 ASK 0.37 0.17 1.37 1.15E-01 0.63
SIR-2 ASK 0.33 0.12 1.23 4.25E-01 0.44
10
PHA-4 && HLH-4[SoT] CAN 0.55 0.10 2.68 1.78E-03 0.5
PHA-4 CAN 0.22 0.10 1.09 7.41E-01 0.5
HLH-4 CAN 0.21 0.17 1.05 7.23E-01 0.83
13
MDL-1 && PHA-4 [SoT] ALM 0.50 0.10 2.11 1.65E-02 0.43
MDL-1 ALM 0.26 0.17 1.08 6.30E-01 0.71
PHA-4 ALM 0.29 0.10 1.20 5.16E-01 0.43
Table 4: The 8 distance refined single-motif rules. Take the first rule as an example; it is the refinement of rule 3 in Table 2
where the distance of the motif PUF-11 from SoT is constrained to be between 350 and 950 bps.
ID Motif Cell Type Confidence Support Lift p-value
Within cell
Support
3 PUF-11 ASE 0.67 0.1356 1.97 7.22E-3 0.4
3(refined) PUF-11 [350-950] SoT ASE 0.88 0.12 2.58 5.73E-04 0.35
5 MEX ASE 0.58 0.1186 1.72 4.51E-2 0.35
5(refined) MEX [250-900] SoT ASE 0.88 0.12 2.58 5.73E-04 0.35
6 HLH-19 PHA 0.58 0.1186 2.6 6.76E-4 0.54
6(refined) HLH-19 [190-750] SoT PHA 0.70 0.12 3.18 5.95E-05 0.54
7 PUF-11 PHA 0.50 0.1017 2.27 8.82E-3 0.46
7(refined) PUF-11 [100-850] SoT PHA 0.60 0.10 2.72 1.48E-03 0.46
11 LIN-32 CAN 0.50 0.1356 2.46 5.55E-4 0.67
11(refined) LIN-32 [0-430] SoT CAN 0.55 0.10 2.68 5.32E-04 0.50
12 PHA-4 ALM 0.50 0.1356 2.11 3.81E-3 0.57
12(refined) PHA-4 [520-900] SoT ALM 0.70 0.12 2.95 1.61E-04 0.50
14 PHA-4 ADL 0.46 0.1017 1.95 3.14E-2 0.43
14(refined) PHA-4 [50-1000] SoT ADL 0.50 0.10 2.11 1.65E-02 0.43
15 PHA-4 AIY 0.22 0.1017 1.87 2.38E-2 0.86
15(refined) PHA-4 [240-850] SoT AIY 0.26 0.10 2.20 6.93E-03 0.86
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
86
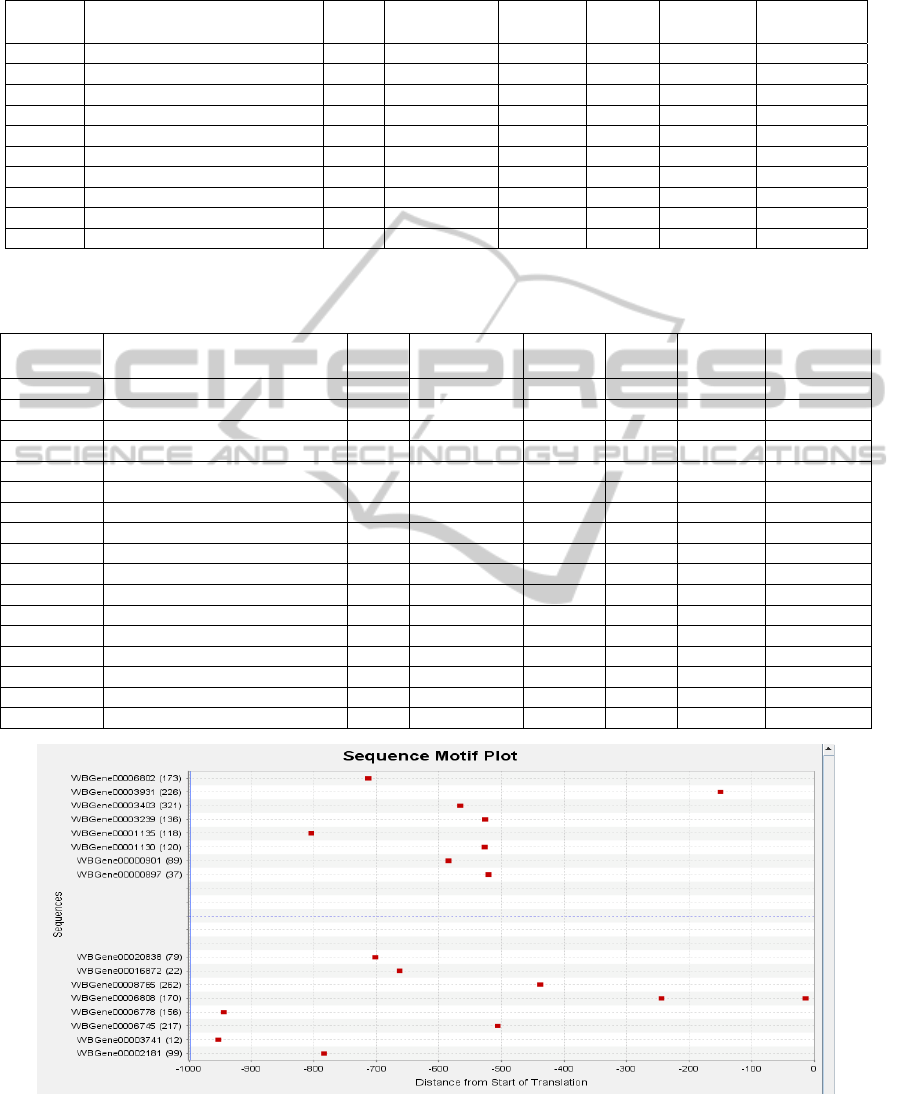
Table 5: Selected mined rules: these rules were selected by the Benjamini and Hochberg’s procedure applied to the 51
mined rules using q = 0.05. This means that the probability of making a Type I error here is less than 0.05.
ID in
Table 2
Motif
Cell
Type
Confidence Support Lift p-value
Within cell
support
2 HLH-14 && HLH-19 [SoT] PHA 0.8571 0.1017 3.8901 1.49E-05 0.54
1 PHA-4 && CND-1 [SoT] ASE 1.0000 0.1017 2.9500 3.07E-04 0.30
4 HNF-6 && HLH-4 [SoT] HSN 0.6667 0.1017 3.0256 4.49E-04 0.46
11 LIN-32 CAN 0.5000 0.1356 2.4583 5.55E-04 0.67
6 HLH-19 PHA 0.5833 0.1186 2.6474 6.76E-04 0.54
10 PHA-4 && HLH-4 [SoT] CAN 0.5455 0.1017 2.6818 1.78E-03 0.50
9 PHA-4 && SIR-2 [SoT] ASK 0.6667 0.1017 2.4583 3.74E-03 0.38
12 PHA-4 ALM 0.5000 0.1356 2.1071 3.81E-03 0.57
3 PUF-11 ASE 0.6667 0.1356 1.9667 7.22E-03 0.40
7 PUF-11 PHA 0.5000 0.1017 2.2692 8.82E-03 0.46
Table 6: Selected distance refined rules along with mined rules: these rules were selected by the Benjamini and Hochberg’s
procedure applied to the rule set which consists of 51 mined rules, the rules generated from multi-motif rules (from Table
3), and 8 distance refined rules (from Table 4) using q = 0.05.
ID in
Table 2
Motif
Cell
Type
Confidence Support Lift p-value
Within cell
support
2 HLH-14 && HLH-19 [SoT] PHA 0.8571 0.1017 3.8901 1.49E-05 0.54
6(refined) HLH-19 [190-750] [SoT] PHA 0.70 0.12 3.18 5.95E-05 0.54
12(refined) PHA-4 [520-900] [SoT] ALM 0.70 0.12 2.95 1.61E-04 0.50
1 PHA-4 && CND-1 [SoT] ASE 1 0.1017 2.95 3.07E-04 0.3
4 HNF-6 && HLH-4 [SoT] HSN 0.6667 0.1017 3.0256 4.49E-04 0.46
11(refined) LIN-32 [0-430] [SoT] CAN 0.55 0.10 2.68 5.32E-04 0.50
11 LIN-32 CAN 0.5 0.1356 2.4583 5.55E-04 0.67
3(refined) PUF-11 [350-950] [SoT] ASE 0.88 0.12 2.58 5.73E-04 0.35
5(refined) MEX [250-900] [SoT] ASE 0.88 0.12 2.58 5.73E-04 0.35
6 HLH-19 PHA 0.5833 0.1186 2.6474 6.76E-04 0.54
7(refined) PUF-11 [100-850] SoT PHA 0.60 0.10 2.72 1.48E-03 0.46
10 PHA-4 && HLH-4 [SoT] CAN 0.5455 0.1017 2.6818 1.78E-03 0.5
9 PHA-4 && SIR-2 [SoT] ASK 0.6667 0.1017 2.4583 3.74E-03 0.38
12 PHA-4 ALM 0.5 0.1356 2.1071 3.81E-03 0.57
15 PHA-4 [240-850] [SoT] AIY 0.26 0.10 2.20 6.93E-03 0.86
3 PUF-11 ASE 0.6667 0.1356 1.9667 7.22E-03 0.4
7 PUF-11 PHA 0.5 0.1017 2.2692 8.82E-03 0.46
Figure 3: Sequence plot for the rule PHA-4→ALM. Each red dot is an occurrence of the motif PHA-4 in the promoter
regions of the genes listed on the Y-axis. The X-axis represents the distance of the motifs from SoT, and the Y-axis lists the
gene sequences that contain the motif PHA-4. The sequences above the dotted line are expressed in cell type ALM, while
the sequences below the dotted line are not. From this plot, we can see that if we refine the rule by specifying the location of
the motif PHA4 at a distance of between 500 to 900 bps from SoT, then the rule is improved.
MiningAssociationRulesthatIncorporateTranscriptionFactorBindingSitesandGeneExpressionPatternsinC.elegans
87

5.3 Controlling the False Discovery
Rate
As described in Section 4, we applied the Benjamini
and Hochberg’s correction to all 51 mined rules
using a significant level q = 0.05. Ten rules were
selected as significant and they are shown in Table
5.
We also applied Benjamini and Hochberg’s
correction to the rule set of the 51 mined rules
combined with the refined rules generated by the
previous two analysis methods, using q = 0.05.
Seventeen rules were selected, as shown in Table 6.
These rules are statistically interesting and warrant
further investigation of their biological significance.
Interestingly, most of the distance refined rules
were selected in Table 6, where their corresponding
original rules were not, suggesting that distance
from the SoT may play an important role in gene
expression. One caveat to this conclusion is that the
refined rules were chosen after looking at the data to
determine where motifs are found, which may
artificially lower the p value. Ideally, refined rules
should be tested on a novel data set.
5.4 Hypothesis-driven Analysis
Our analysis tool provides a way to test hypotheses
relating motifs and cell types, even if these
hypotheses are not mined by our system. As an
illustration, we use here a pattern described by
Hobert et al. (Hobert et al., 2010) and shown in
Table 7: the two TFs CEH-10 and TTX-3 work
together in regulating gene expression in cell type
AIY, but work separately in several other cell types
examined. Hobert et al. also found that those two
TFs always bind together in the genes expressed on
cell type AIY, so they combined their binding sites
and proposed a PWM which represents the two
binding sites. We can express this finding in the
form of an association rule by using Hobert’s
proposed PWM and the rule CEH-10/TTX-3→AIY.
We evaluated the statistical significance of this rule
in our dataset described in section 3. We constructed
5 rules, one rule for each cell type in Table 7, as
shown in Table 8. We used our system to calculate
each of the rules’ metrics with respect to our dataset.
The third rule, corresponding to the pattern found in
(Hobert et al., 2010), has the best metrics and a p-
value of 0.00253, while the other rules are not
significant at a p-value0.05. Thus, our association
rules and their metrics are consistent with
biologically confirmed findings.
Table 7: Gene expression patterns taken from (Hobert et
al., 2010).1 means that the TF has been bound in the gene
regulatory region and 0 means that is has not.
CAN ADL AIY AIA ASE
CEH-10 1 0 1 0 0
TTX-3 0 1 1 1 0
6 CONCLUSIONS
In this paper we have presented a framework for
discovering rules governing gene expression patterns
based on transcription factor position weight
matrices. This framework uses the MAST tool
(Bailey, 1998) to annotate motifs in each gene
promoter sequence, and then mines association rules
to find relations between transcription factors and
cell type specific expression. We analyzed the
significance of the association rules we obtained.
Also, we showed another use of our system to
evaluate gene expression relations between
transcription factors and cell types found in the
literature.
Future work includes extending our dataset by
collecting more complete regulatory sequences,
more cell type classes and expressed sequences, and
more transcription factors, as more binding sites
become better defined. Applying other data mining
techniques in addition to association rule mining will
be investigated as well.
Table 8: Association rules constructed and tested. Each rule corresponds to a cell type in Table 7.
Motif Cell Type Confidence Support Lift p-value Within cell Support
CEH-10/TTX-3 CAN 0.4 0.0678 1.9667 9.01E-02 0.33
CEH-10/TTX-3 ADL 0.3 0.0508 1.2643 6.09E-01 0.21
CEH-10/TTX-3 AIY 0.4 0.0678 3.3714 2.53E-03 0.57
CEH-10/TTX-3 AIA 0.2 0.0339 2.36 1.51E-01 0.4
CEH-10/TTX-3 ASE 0.1 0.0169 0.295 7.98E-02 0.05
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
88

REFERENCES
Agrawal, R., & Srikant, R. (1994). Fast algorithms for
mining association rules. Proc. 20th Int. Conference
on very Large Data Bases (VLDB), 1215, 487-499.
Agrawal, R., Imielinski, T., & Swami, A. (1993). Mining
association rules between sets of items in large
databases. SIGMOD Rec., 22(2), 207-216. doi:
http://doi.acm.org/10.1145/170036.170072
Altun, Z. F., & Hall, D. H. (2011). Nervous system,
general description. (). WormAtlas. doi:
10.3908/wormatlas.1.18
Alvarez, S. A. (2003). Chi-squared computation for
association rules: Preliminary results. (Technical
Report No. BC-CS-2003-01).Computer Science
Department, Boston College.
Arda, H. E., & Walhout, A. J. M. (2010). Gene-centered
regulatory networks. Briefings in Functional
Genomics, 9(1), 4-12.
Bailey, T. T. L. (1998). Combining evidence using p-
values: Application to sequence homology searches.
Bioinformatics (Oxford, England), 14(1), 48-54.
Bamps, S., & Hope, I. A. (2008). Large-scale gene
expression pattern analysis, in situ, in caenorhabditis
elegans. Briefings in Functional Genomics &
Proteomics, 7(3), 175-183.
Benjamini, Y., & Hochberg, Y. (1995). Controlling the
false discovery rate: A practical and powerful
approach to multiple testing. Journal of the Royal
Statistical Society.Series B (Methodological), , 289-
300.
Bigelow, H., Wenick, A., Wong, A., & Hobert, O. (2004).
CisOrtho: A program pipeline for genome-wide
identification of transcription factor target genes using
phylogenetic footprinting. BMC Bioinformatics, 5(1),
27.
Conrad, R., Lea, K., & Blumenthal, T. (1995). SL1 trans-
splicing specified by AU-rich synthetic RNA inserted
at the 5'end of caenorhabditis elegans pre-mRNA.
Rna, 1(2), 164-170.
Hobert, O., Carrera, I., & Stefanakis, N. (2010). The
molecular and gene regulatory signature of a neuron.
Trends in Cognitive Sciences, 33(10), 435.
Hope Laboratory Expression Pattern Database. Retrieved
from http://bgypc059.leeds.ac.uk/~web/databaseintro.
htm
Hunt-Newbury, R., Viveiros, R., Johnsen, R., Mah, A.,
Anastas, D., Fang, L., Lorch, A. (2007). High-
throughput in vivo analysis of gene expression in
caenorhabditis elegans. PLoS Biology, 5(9), e237.
A. Icev*, C. Ruiz , and E. Ryder. (2003). Distance-
Enhanced Association Rules for Gene Expression.
In Proc. of the Third ACM SIGKDD Workshop on
Data Mining in Bioinformatics (BIOKDD2003). Held
in conjunction with the Ninth International Conference
on Knowledge Discovery and Data Mining
(KDD2003). pp. 34-40. Washington DC, USA. August
2003
Ihuegbu, N. E., Stormo, G. D., & Buhler, J. (2012). Fast,
sensitive discovery of conserved genome-wide motifs.
Journal of Computational Biology, 19(2), 139-147.
MacIsaac, K. D., Lo, K. A., Gordon, W., Motola, S.,
Mazor, T., & Fraenkel, E. (2010). A quantitative
model of transcriptional regulation reveals the
influence of binding location on expression. PLoS
Computational Biology, 6(4), e1000773.
Newburger, D. E., & Bulyk, M. L. (2009). UniPROBE:
An online database of protein binding microarray data
on protein–DNA interactions. Nucleic Acids Research,
37(suppl 1), D77-D82.
K. A. Pray*, C. Ruiz. (2005). Mining Expressive
Temporal Associations From Complex
Data. International Conference on Machine Learning
and Data Mining MLDM'2005.
Springer Verlag.
Leipzig, Germany. July 9-11, 2005
Reece-Hoyes, J. S., Deplancke, B., Shingles, J., Grove, C.
A., Hope, I. A., & Walhout, A. J. M. (2005). A
compendium of caenorhabditis elegans regulatory
transcription factors: A resource for mapping
transcription regulatory networks. Genome Biology,
6(13), R110.
Reece-Hoyes, J. S., Shingles, J., Dupuy, D., Grove, C. A.,
Walhout, A. J. M., Vidal, M., & Hope, I. A. (2007).
Insight into transcription factor gene duplication from
caenorhabditis elegans promoterome-driven
expression patterns. BMC Genomics, 8(1), 27.
D. Thakkar*, C. Ruiz, E. F. Ryder. (2007). Hypothesis
Driven Specialization of Gene Expression Association
Rules. In Proceedings of the IEEE International
Conference on Bioinformatics and Biomedicine
(BIBM2007). pp. 48-55. Fremont, CA. USA. Nov.
2007.
The C. elegans Sequencing Consortium. (1998). Genome
sequence of the nematode C. elegans: A platform for
investigating biology. Science, 282(5396), 2012-2018.
doi: 10.1126/science.282.5396.2012
WormBase, http://www.wormbase.org/, release WS230,
date 1 April 2012.
MiningAssociationRulesthatIncorporateTranscriptionFactorBindingSitesandGeneExpressionPatternsinC.elegans
89
