
Planning of Diverse Trajectories
Jan To
ˇ
zi
ˇ
cka, David
ˇ
Si
ˇ
sl
´
ak and Michal P
ˇ
echou
ˇ
cek
Agent Technology Center, Department of Computer Science, Czech Technical University in Prague, Prague, Czech Republic
Keywords:
Trajectory Planning, UAV, Human-machine Interface.
Abstract:
Unmanned aerial vehicles (UAVs) are more and more often used to solve different tasks in both the private and
the public sector. Some of these tasks can often be performed completely autonomously while others are still
dependent on remote pilots. They control an UAV using a command display where they can control it manually
using joysticks or give it a simple task. The command display allow for the planning of the UAV trajectory
through waypoints while avoiding no-fly zones. Nevertheless, the operator can be aware of other preferences
or soft restrictions for which it’s not feasible to be inserted into the system especially during time critical tasks.
We propose to provide the operator with several different alternative trajectories, so he can choose the best
one for the current situation. In this contribution we propose several metrics to measure the diversity of the
trajectories. Then we explore several algorithms for the alternative trajectories creation. Experimental results
in two grid domains show how the proposed algorithms perform.
1 INTRODUCTION
Unmanned aerial vehicles (UAVs) are more and more
often used in military operations, in humanitarian and
rescue missions, and in private sector tasks. Some
of the tasks, e.g. the photo-mapping, can often be
performed completely autonomously, while others are
still dependent on remote pilots. They control an UAV
using a command display where they can control it
manually using joysticks or give it a simple task, e.g.
to fly through a sequence of points on the map.
A human operator (pilot) seems to be a bottle-
neck of the system when several UAVs collaborate
on a single mission. Each operator or a team of op-
erators is responsible for one UAV and controls its
actions. The human operators communicate among
themselves and coordinate their actions in order to
achieve a common goal. The whole system contain-
ing UAVs and all HMI machines used to control the
UAVs is called Unmanned Aerial System (UAS). One
of the main goals of research tackling UAVs is to im-
prove the UAS so that a controller or a group of con-
trollers can control larger groups of UAVs easily. This
can be achieved by two means:
• increase UAV autonomy,
• improve human–machine interface (HMI).
In this article we explore a solution which is over-
lapping both of these approaches. It increases the au-
tonomy of UAS as a whole by extension of UAV plan-
ning capability (still not increasing its own autonomy)
and changes the HMI. We will focus on the problem
of the trajectory planning. Usually, all UAVs are con-
trolled directly by remote operators (pilots) or they
can fly following predefined trajectories. In the latter
case, once the operator realizes that a trajectory needs
to be changed, it can define a new trajectory, e.g. by
means of waypoints and no-fly zones. When the way-
points are updated, the new trajectory is planned (on
UAV or within ground control station). If the operator
agrees with the trajectory it is applied. If the operator
does not want to use the planned trajectory he can re-
ject it and specify a new set of waypoints or introduce
a new no-fly zone to get the trajectory matching his
preferences better.
Even thought the planned trajectory is the optimal
solution with respect to the fuel consumption, needed
time, or other user specified criteria, the operator can
be aware of other preferences, where the plane should
fly, or soft restrictions on areas which would be nice
to avoid. These can contain, for example, possible fu-
ture colliding traffic, weather conditions, flights over
inhabited areas, etc. It is not feasible to insert all
these preferences into the system, especially during
time critical tasks. The operator typically does not
accept proposed trajectory in the cases when he sees
other which is suboptimal but more preferable one.
Then he has to change input values to force the sys-
tem to give the desired solution. This can be repeated
several times before the trajectory meets all the oper-
120
Toži
ˇ
cka J., Šišlákand D. and P
ˇ
echou
ˇ
cek M..
Planning of Diverse Trajectories.
DOI: 10.5220/0004254601200129
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 120-129
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: New generation of HMI displays will allow a user
to select from several proposed trajectories when the cur-
rent trajectory needs to be replanned. This figure illustrate
a situation when a new no-fly zone (orange circle) has been
inserted. Since the current UAV trajectory (black colored
stripe) is crossing this new no-fly zone, the trajectory has to
be replanned. Along with the optimal trajectory (cyan tra-
jectory) several alternatives (green trajectory) will be pro-
posed to the user. He can then easily choose new trajectory
based on his own preferences, stay with the current one, or
change the definition of the trajectory by changing its way-
points or by adding new no-fly zone or removing an existing
one.
ator’s criteria and preferences.
This iterative process can be improved by a system
giving several possible trajectories out of which the
operator selects one based on his preferences which
is then applied. These proposed trajectories should be
different by means of operator perception and prefer-
ences. For example, imagine an UAV flying directly
through a no-fly zone. Shorter way to go around this
no-fly zone is the southern way but the operator sees
that the northern way is just a bit longer and he knows
(based on his experience) that the southern trajectory
can later collide with some other currently unknown
traffic for the planner. Currently used trajectory plan-
ners, e.g. A* (Hart et al., 1968), or Θ* (Nash et al.,
2007), would propose the optimal trajectory, i.e. the
southern one. It can be quite difficult for the opera-
tor to make the UAV to pass around the no-fly zone
by north – he can add an extra way-point or block the
southern direction by new a no-fly zone. At this mo-
ment, it would be very helpful for the operator to have
a possibility to select between the optimal southern
way and an alternative northern way as it’s illustrated
in Figure 1.
It is very difficult to create several plans which are
different enough and understandable from the human
operator’s perspective. Currently there are several al-
gorithms allowing to give k-best solutions but in our
domain all these solution would be usually very sim-
ilar to the best one and can be even indistinguishable
for the human operator. They would typically differ
in a small speed change or in an unobservable devia-
tion from the optimal trajectory. What we really need
are the alternatives which are different from the oper-
ator’s perspective.
The goal of our work is to extend a common tra-
jectory planner so it allows us to create distinguish-
ably different trajectories. Firstly, we need to define
what different actually means. The notion of differ-
ence is connected to the human perception and thus
can be individual. However, it’s necessary to formally
define it.
In this contribution we propose several metrics
measuring how much the trajectories differ and sev-
eral approaches to generate different trajectories. We
start with the definition of several trajectory diver-
sity metrics in Section 2. In Section 3, we describe a
trajectory metric based approach which penalizes the
trajectories similar to the previously generated ones.
Section 4 describes an approach which systematically
extends obstacles and then uses any traditional opti-
mal trajectory planner to find individual alternative
trajectories. The last approach, described in Sec-
tion 5, extends this idea by using the Voronoi and the
Delaunay graphs. All the proposed approaches are
evaluated using the presented metrics in two experi-
mental domains and the results are examined in Sec-
tion 6.
For the time being, we focus on a 4-grid and 8-
grid domains (Yap, 2002) and we’ll generalize it to
real coordinates later. We decided to use this domain
because the grid domains are often used as bench-
mark tasks for the trajectory planners. They are often
more complicated than real world domains because
they often contain several optimal paths. Neverthe-
less, proposed algorithms do not change the planners
and thus any planner for more complicated domains
can be used. Figures 2–4 and 6 illustrate which trajec-
tories would be given by each proposed planner in the
4-grid and the 8-grid world with few obstacles (repre-
senting no-fly zones).
Obviously, similar approach can be used in other
real world domains where a system proposes a solu-
tion to a human operator. The operator typically has
broader knowledge about the task and the related en-
vironment. Thus, giving the operator several possibil-
ities can help him to choose the best overall solution.
2 TRAJECTORY DIVERSITY
METRICS
In this section, we introduce several approaches to the
trajectory comparison. We will use definitions simi-
lar to those used in (Coman and Mu
˜
noz-Avila, 2011),
which defines the diversity metric for a general plan
PlanningofDiverseTrajectories
121

as follows. Let D : π × π → [0,∞) be a metric de-
scribing the distance between two trajectories. For
a non-empty set of trajectories Π, Coman in (Coman
and Mu
˜
noz-Avila, 2011) defines the plan-set diversity
Div
D
(Π) as:
Div
D
(Π) =
∑
π,π‘∈Π
D(π,π‘)
|Π|×(|Π|−1)
2
,
and the relative diversity RelDiv
D
(π,Π) of plan π rel-
ative to plan-set Π:
RelDiv
D
(π,Π) =
∑
π‘∈Π
D(π,π‘)
|Π|
where |Π| stands for the number of plans in the plan-
set.
We will use the plan-set diversity to aggregate tra-
jectory distances over the whole set of trajectories.
2.1 Metric: Different States
The different states metric D
States
takes into consider-
ation states of the plans only. In the case of trajectory,
the plan state is the robot location together with some
other attributes, e.g. direction, battery level, etc. In
our experimental domains, the state represents a 2D
location only. Metric D
States
then counts the number
of states of one plan which are also in the other plan
and transforms it into a distance metric:
D
States
(π,π‘) = 1 −
∑
s∈π
(
1 for s ∈ π‘
0 for s /∈ π‘
|π|
where the |π| stands for the number of states in the
path.
This metric is very general and can be used to
any planning problem, not necessarily to the trajec-
tory planning. In the continuous domain, it would
be useful to add a threshold determining which plane
states are considered to be the same, e.g. based on the
position and heading of the planes.
2.2 Metric: Trajectory Distance
The trajectory distance metric D
Distance
is a general-
ization of the different states metric. It requires some
knowledge about the domain – the distance metric be-
tween the states δ(s
1
,s
2
). For each state in the first
plan it counts it’s distance to the second plan, i.e. the
distance to the closest state of the other plan.
D
Distance
(π,π‘) =
∑
s∈π
min
s‘∈π‘
δ(s,s‘)
2.3 Metric: Obstacle Avoidance
The obstacle avoidance metric D
Obstacles
takes also
into consideration how obstacles are avoided by each
trajectory. This idea is based on the human percep-
tion of what are different trajectories. Most of the tra-
jectories well evaluated by the metrics described in
the previous sections are perceived to be very simi-
lar and quite unreasonable – just worsening the op-
timal trajectory without changing anything signifi-
cantly. Human preferred alternatives are often de-
scribed by means of how the obstacles are avoided.
Therefore we need a metric that captures that the ob-
stacles have been avoided from some side. For that we
need to specify what the ’same side’ exactly means.
We say that a robot passes obstacle o by direction d
when a ray going from o in direction d crosses the tra-
jectory. Metric D
Obstacles
is then defined as follows:
D
Obst.
(π,π‘) = 1−
∑
o∈O
∑
d∈D
1 if π passes o by d
⇔ π‘ passes o by d
0 otherwise
|O||D|
where the O is the set of all obstacles and D is a set of
all directions we are testing. In our experiments, we
use the set of four directions: north, east, south and
west.
3 METRICS BASED PLANNERS
In this section, we introduce a most general ap-
proaches to the trajectory comparison. They are
solely based on the metrics described in Section 2.
This is the most general case which can be easily gen-
eralized to be applied in a general STRIPS planning
problem (Fikes and Nilsson, 1971).
Firstly this planner, listed as Algorithm 1, finds
the optimal trajectory π
∗
using provided trajectory
planner. Then it iteratively looks for other diverse
trajectories. It updates the goal function to use the tra-
jectory distance metric D together with the current set
of found trajectories Π. The goal function for every
trajectory π is then calculated as the relative diversity
RelDiv
D
(π,Π).
Let’s have a metric D : π × π → [0, ∞) evaluating
the distance of two trajectories and the relative diver-
sity metric RelDiv(π,Π) as described in Section 2.
We can use it in a planning algorithm to get the next
optimized trajectory which is different enough with
respect to Π trajectories already calculated. This can
easily be done by defining the new evaluating func-
tion
g
D
(π) = g(π) + α(MaxDiv − RelDiv
D
(π,Π)),
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
122
Algorithm 1: Trajectory distance metric based di-
verse trajectory planner.
Data: G – state graph
Data: O – set of obstacles
Data: start,target – start and target states
Data: planner – any trajectory planner
Data: n – required number of trajectories
Data: D – trajectory distance metric
Result: Π – set of trajectories
π
∗
← planner.findPath(G, O, start,target) ;
Π = {π
∗
} ;
while |Π| < n do
planner.updateGoalFunction(D,Π) ;
π ← planner.findPath(G,O, start,target) ;
Π ← Π ∪ {π} ;
end
return Π ;
where g(π) is the original price of the trajectory (e.g.
it’s length) and α is the weight of the RelDiv relative
diversity metric value which is transformed into the
penalty by being subtracted from MaxDiv, the maxi-
mal value of the D metric, which is 1 for most of our
cases.
The pro of trajectory based metrics is that, unlike
the other metrics described in the following sections,
they can create different trajectories also for domains
without any obstacles.
3.1 Trajectory Distance Metric Planner
Trajectory distance metric planner uses D
Distance
tra-
jectory distance metric. Trajectories created when us-
ing this metric are very sensitive to the α value. They
can be very suboptimal when the value of α is large.
We can avoid this problem if we omit the trajecto-
ries much worse than the optimal one, e.g. trajecto-
ries more than 20 % longer than the optimal trajectory.
Note that we know the quality of the optimal trajec-
tory because it’s found as the first trajectory, before
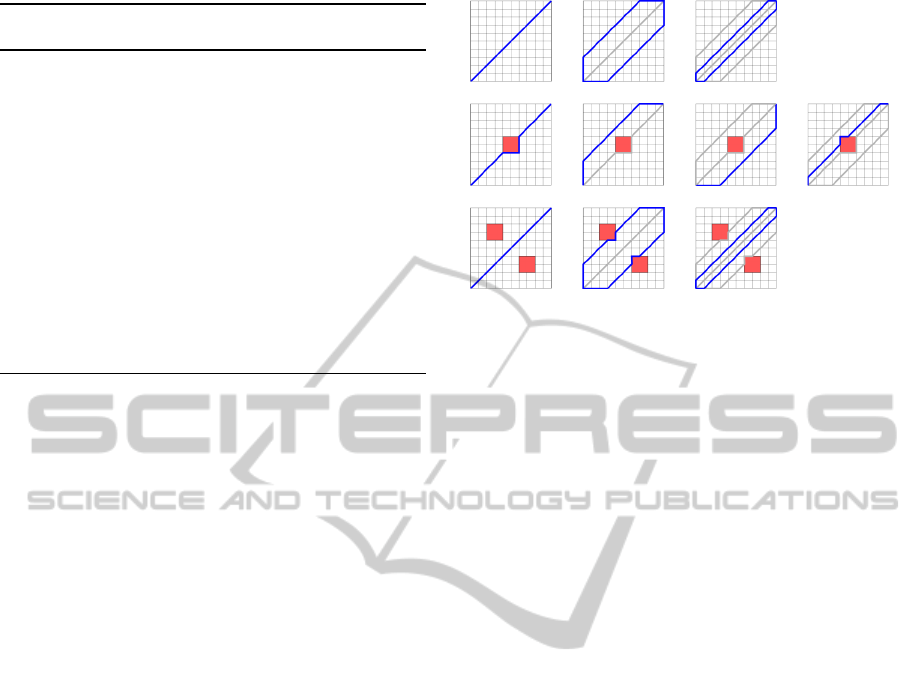
any metric is used. See Figure 2 for illustration how
the planner with this metric would work.
In our experiments we limit the maximal diversity
value to 2 (MaxDiv in the updated goal function g
D
).
All the Div
D
values bigger than 2 are considered to be
2 and thus result in 0 penalty.
3.1.1 Trajectory Distance Metric MaxMin
Planner
The trajectory distance metric planner tries to mini-
mize the penalty derived from the Div
D
Distance
diversity
function. That means that it tries to find a trajectory,
which is in average the most different to the previ-
ously found trajectories. Another possibility is to look
Figure 2: Trajectory distance metric. Blue lines show the
trajectories created during the subsequent runs of the trajec-
tory planner. Dark gray lines show the trajectories forming
the set Π, i. e. the trajectories created during previous it-
erations. We can see that this method is very sensitive to
the threshold specifying how much created trajectory can
differ from the optimal one. In the 2-obstacles case the al-
lowed deviation from the optimal price is not large enough
to cover the cases where the obstacles are passed around.
Note, that even if the algorithm would run more iterations,
such a solution would not be found.
for a trajectory which is the most different to the most
similar trajectory, i.e. to compute the RelDiv
D
func-
tion as the minimal distance instead of their average:
RelDiv
Min
D
(π,Π) = min
π‘∈Π
D(π,π‘)
On our illustrative cases, this planner behaves sim-
ilarly to the trajectory distance metric planner (Fig-
ure 2). Nevertheless in our experiments it showed
better performance, especially with respect to the ob-
stacle avoidance metric.
3.2 Different State Metric Planner
The different state metric planner, based on the D
States
metric, is illustrated in Figure 3. We can see that most
of the trajectories are very similar and human opera-
tor would not consider them as real alternatives to the
optimal trajectory.
4 OBSTACLE EXTENSION
APPROACH
This approach works differently than the previous
ones. It transforms the planning task into several new
tasks and then runs a traditional trajectory planner to
find the optimal trajectory in each transformed task as
illustrated by Algorithm 2.
PlanningofDiverseTrajectories
123

Figure 3: Different state metric. Blue and dark gray lines
have the same meaning as in Figure 2. It needs several it-
erations to find a solution avoiding the 2-obstacles case by
going around – which is better behavior than we observed
in the trajectory distance metric described in Section 3.1.
Algorithm 2: Obstacle extension based diverse tra-
jectory planner.
Data: G – state graph
Data: O – set of obstacles
Data: start,target – start and target states
Data: planner – any trajectory planner
Data: directions – possible extension directions
Result: Π – set of trajectories
O
∗
← allObstacleExtensions(O,directions) ;
Π = {} ;
forall O
0
∈ O
∗
do
π ← planner.findPath(G,O
0
,start,target) ;
Π ← Π ∪ {π} ;
end
return Π ;
The transformed task contains obstacles extended
in different directions. Having that each obsta-
cle can be extended to one of 4, or 8, pos-
sible directions, the algorithm tries all possible
combinations of extensions (generated by function
allObstacleExtensions(O,directions)) and for each
combination it takes the shortest trajectory found by
the trajectory planner. This approach is very compu-
tational power demanding – it needs to run the tra-
jectory planner d
k
-times, where d is the number of
directions, where the obstacles can be expanded, and
k is the number of obstacles. Many cases will result
in the same trajectories or in no solution at all. On
the other hand it allows to create many different al-
ternatives which cannot be found by the previously
described planners. Figure 4 shows how the obstacles
are extended and corresponding trajectories found by
the trajectory planner.
Figure 4: Obstacle extension approach. The blue line is a
trajectory found by the trajectory planner for a task, where
the obstacles are extended in the direction of continuous red
lines. Dashed red lines show other possible obstacle exten-
sions producing the same trajectory. In the 2-obstacles case,
we can see that this approach proposed also a S-shaped tra-
jectory which has not been proposed by any other approach
yet. Even though this trajectory is much longer than the
shortest one and thus would not be probably chosen by the
operator, it well demonstrates that this approach is more
general than the previous ones.
5 VORONOI–DELAUNAY GRAPH
BASED TRAJECTORIES
For each point in the space we can find the closest ob-
stacle to that point. Voronoi diagram (Aurenhammer,
1991) is a decomposition of the space into disjunc-
tive Voronoi areas containing points with the same
closest obstacle. The Voronoi graph is composed of
the borders between the Voronoi areas. The edges
represent an abstraction of each passage between the
obstacles. Since this graph is discreet even for 2D
space, it is often used for the trajectory planning (Gar-
rido et al., 2006; Hui-ying et al., 2010). The Delau-
nay graph (Fortune, 1997) is an inverted graph to the
Voronoi graph. The vertexes represent the centers of
Voronoi areas, i. e. the obstacles in our case, and the
edges show which two Voronoi areas have a common
border. For planning alternative trajectories, the algo-
rithm works with the extended Voronoi graph, where
start and target points are connected to the graph. The
Delaunay graph is extended to contain edges connect-
ing centers of outermost Voronoi areas (those which
are crossing the planning area border) towards the
borders
1
.
We propose to use the extended Voronoi and the
Delaunay graphs in the problem of finding diverse tra-
jectories as described in Algorithm 3.
Firstly, the algorithm creates the extended Voronoi
graph G
V
in the method createExtendedVoronoi-
Graph, which connects also the start and the target
1
Additional nodes are placed on the intersection of the
border and the added edge into the Delaunay graph.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
124
states
2
. Then, it finds all the paths P
V
from the start to
the target in the extended Voronoi graph G
V
. For each
path π
V
, it creates the extended Delaunay sub-graph
G
π
where it omits the edges which would cross that
path π
V
(the method removeDualEdges). The edges
of this new graph G
π
represent new obstacles. The
method convertEdgesToObsacles converts the edges
of the graph into the obstacle set O
π
. Then, using any
trajectory planner planner, it finds the optimal trajec-
tory from the start to the target in the state graph G
avoiding obstacles O and O
π
.
Algorithm 3: Voronoi-Delaunay graph based diverse
trajectory planner.
Data: G – state graph
Data: O – set of obstacles
Data: start,target – start and target states
Data: planner – any trajectory planner
Result: Π – set of trajectories
G
V
←
createExtendedVoronoiGraph(O,start,target) ;
P
V
← findAllPaths(G
V
,start,target) ;
Π = {} ;
forall π
V
∈ P
V
do
G
D
← createDelaunayGraph(G
V
) ;
G
π
← removeDualEdges(G
D
,π
V
) ;
O
π
← convertEdgesToObsacles(G
π
) ;
π ← planner.findPath(G,O ∪ O
π
,start,target)
;
Π ← Π ∪ {π} ;
end
return Π ;
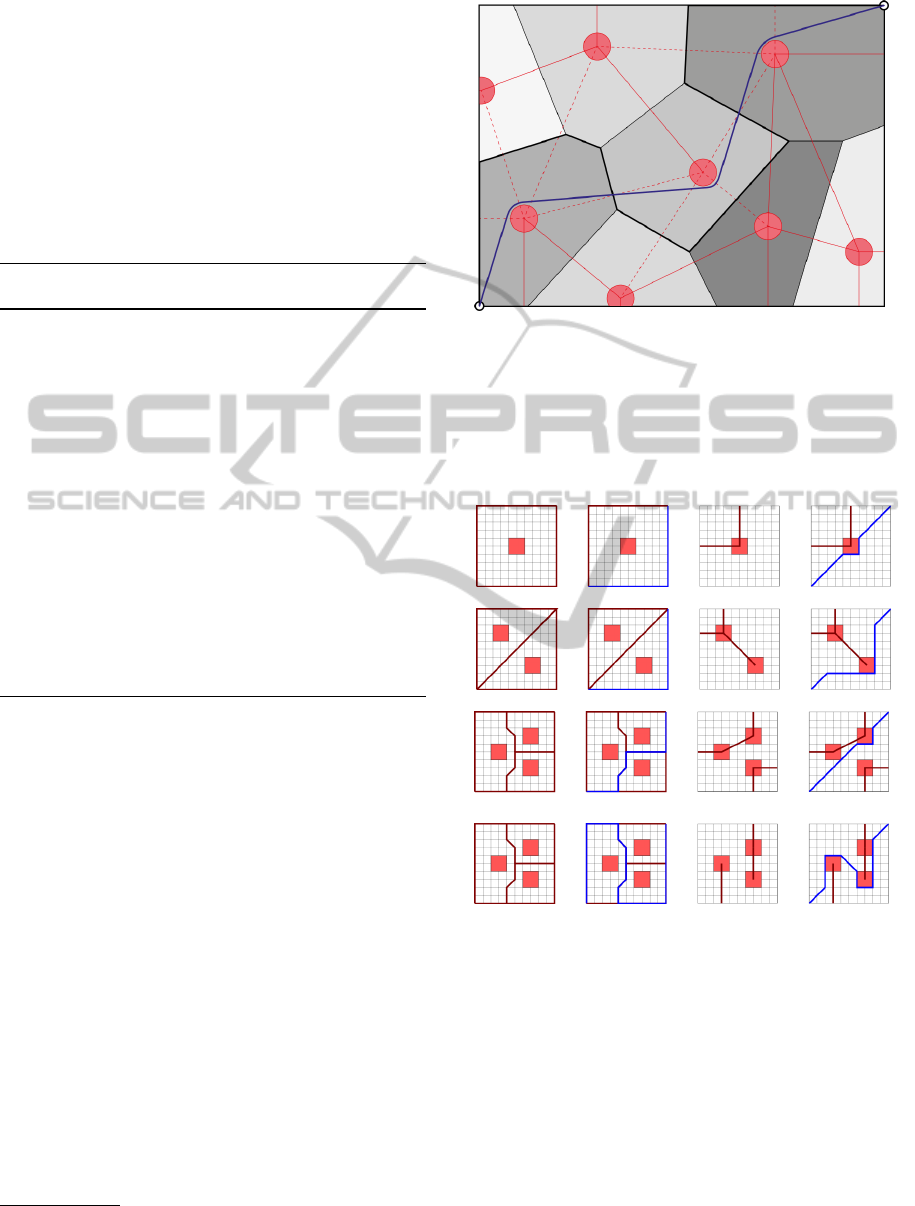
The extended Voronoi and Delaunay graphs with
G
π
from one iteration of the planning algorithm is
shown in Figure 5. Multiple iterations of the algo-
rithm in the 8-grid domain (Yap, 2002) with few ob-
stacles are shown in Figure 6.
We propose to use the Voronoi and the extended
Delaunay graphs in the problem of finding different
trajectories as follows. Firstly, we create the Voronoi
graph and extend it by adding borders of the plan-
ning area, which also connects the start and the tar-
get. Then we find all the paths from the start to the
target and for each path we create obstacle from the
extended Delaunay graph where we omit the edges
which would cross that path. This new graph contains
original obstacles and their extensions, represented by
the edges, similarly to Obstacle Extension Approach
described in Section 4. Then we just find the short-
est path in this new sub-planning problem with any
trajectory planning algorithm. This algorithm is il-
lustrated in Figure 6. This approach is more efficient
than the Obstacle Extension Approach because every
2
For illustrative purposes we add also a border of the
planning area, but this step is optional.
Figure 5: The no-fly zones, represented by the red circles,
define the Voronoi diagram (gray areas). Its dual graph, the
extended Delaunay graph, is shown by the red lines. When
a path (thicker black line) in the Voronoi graph is found, all
the edges of the extended Delaunay graph, that do not cross
that path, are considered to be the obstacles (continuous red
lines) and the shortest path (blue line) is found using any
optimal trajectory planner.
Figure 6: Voronoi–Delaunay graph based trajectories. Each
row demonstrates subsequent steps of the algorithm. The
first column shows the extended Voronoi graph (red lines)
derived from the obstacles. Then all the paths from the start
to the target are found – an example trajectory (blue line)
is shown in the second column. The third column consists
of extended Delaunay graphs (red lines) without the edges
which have been crossed by the current path from the sec-
ond column. Red lines are considered to be obstacles in the
last column, where the alternative trajectory (blue line) is
found by an optimal trajectory planner.
call of the trajectory planner on defined sub-planning
problem will result in a new, original, alternative tra-
jectory.
PlanningofDiverseTrajectories
125

6 EXPERIMENTS
We have evaluated all proposed diverse trajectory
planner in two domains with different number of ob-
stacles. Both domains are based on the 10 × 10 grid
topology, which are often used for the trajectory plan-
ner evaluation: the 4-grid domain which is made of
orthogonal network where each node but the border
ones is connected with 4 neighbors; and the 8-grid do-
main where we allow the diagonal directions too. The
start location is placed to the upper-left corner [0,0]
and the target to the bottom-right corner [10,10]. A
certain number, ranging from 2 to 16, of randomly
generated obstacles are added to each scenario. These
obstacles represent restricted nodes in the grid graph.
During the generation of the obstacles the following
rules had to be fulfilled:
1. no two obstacles can be adjacent, and
2. no obstacle can be on the border line, and
3. there exists a path from start to target (implied by
the previous conditions).
These conditions assure that every obstacle can be
avoided by every side and also that there can be a path
between each pair of obstacles. Each run with a given
number of randomly generated obstacles has been re-
peated 10 times and the average value are presented.
First two graphs (Figures 7 and 8) show how many
alternatives have been found for a different number of
obstacles and how long it took. As expected, values
for the Obstacle extension approach and the Voronoi–
Delaunay graph based approach are growing expo-
nentially with the number of obstacles. The Obsta-
cle extension approach has been evaluated up to 6
obstacles only, since it took too long for the cases
with more obstacles to be evaluated. The computa-
tional complexity of diversity metric based algorithms
is almost constant with a small grow for small num-
ber of obstacles, where the planning algorithm has to
explore larger area before it gets to the target node.
Along with the exponentially growing time complex-
ity of the two algorithms we can see that the num-
ber of found different paths also grows exponentially,
even though it grows only a bit faster for the Obstacle
extension approach, which shows that the Voronoi–
Delaunay graph based approach is more effective.
Since the Voronoi–Delaunay graph based plan-
ner has found too many possible trajectories for even
few obstacles and it would be inappropriate to present
all these trajectories to the user, we decided to limit
the number of evaluated trajectories. Since the main
criteria for the trajectory planning is the trajectory
length, we decided to select 5 or 100 shortest paths
respectively.
The graph in Figure 9 shows the average length
of trajectories given by each planner. And the fol-
lowing graphs (Figures 10–12) show the plan-set di-
versity defined in Section 2 together with one of the
presented trajectory distance metrics.
As expected, the trajectory diversity metric based
algorithms maximized the corresponding metric.
There is one exception in the 8-grid domain with
the trajectory distance metric where, in most cases,
the Voronoi-Delaunay graph based planner had higher
score. This is caused by the limitation of the maximal
distance of trajectories (introduced by the MaxDiv pa-
rameter in the updated goal function) which prevents
creation of trajectories too far from each other.
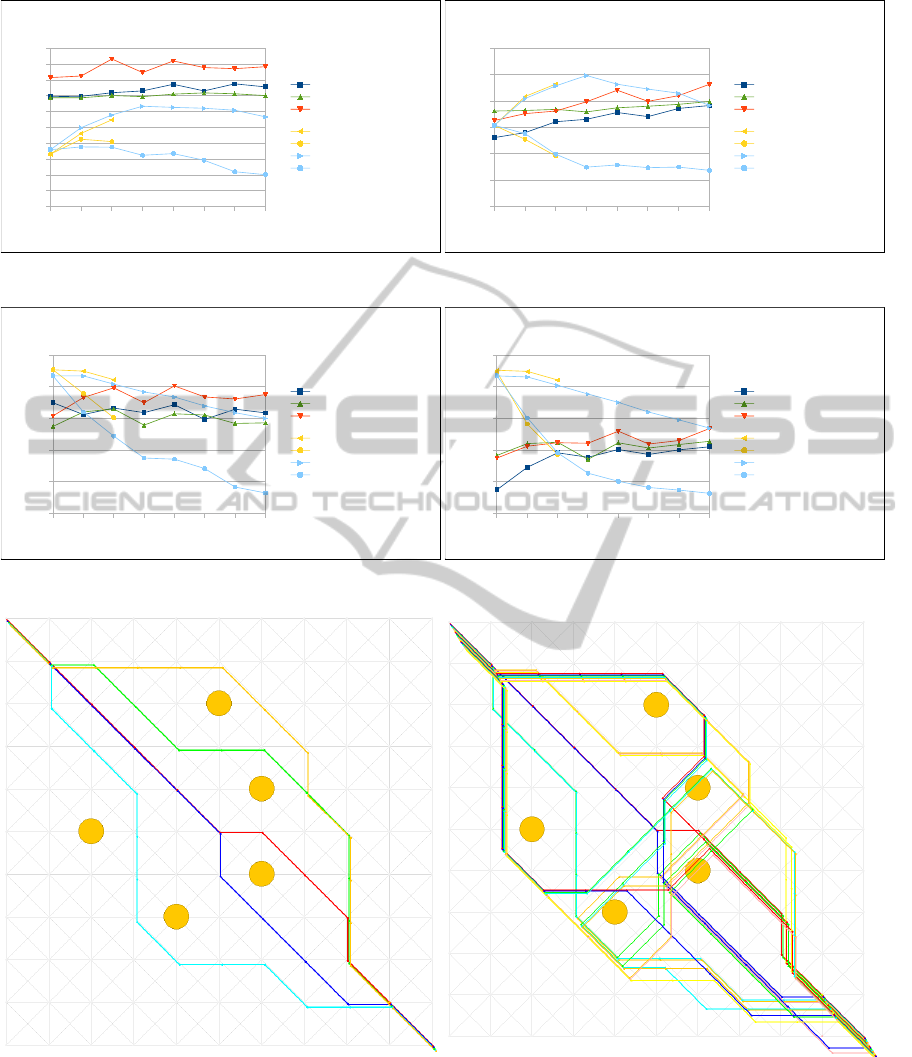
The last Figure 13 shows examples of trajectories
created by the Voronoi-Delaunay graph based diverse
trajectory planner in the scenario with 5 obstacles. We
can see that the 5 shortest trajectories give user a good
selection of different possibilities how to pass the ob-
stacles even though these trajectories were not eval-
uated very well by the presented trajectory diversity
metrics. The reason for that is that even though the
human perception of diversity of trajectories is based
on the trajectory–obstacle relation it is mostly just bi-
nary. Thus if two trajectories avoid any obstacle from
different direction than they are considered to be dif-
ferent. We are now about to proceed with the experi-
ments with human users to verify this hypothesis and,
hopefully, to create a metric which will better reflect
human perception.
7 CONCLUSIONS AND FUTURE
WORK
A human-UAV interaction is a bottleneck of today’s
unmanned aerial systems. The interface during the
trajectory planning can be certainly improved by pro-
viding a user with several alternative trajectories from
which the user can choose the most suitable one. This
problem has not been targeted by the scientific com-
munity yet even though it has a significant practical
impact. This contribution introduces the problem of
planning of the alternative trajectories and proposes
several different approaches to its solution.
In the paper, we proposed several ways how to
measure difference of trajectories and also several ap-
proaches to the planning of alternative trajectories it-
self. We started with the trajectory metric based ap-
proaches which penalize the trajectories similar to
the previously generated ones. Then we focused on
the trajectory-obstacles relations and proposed to add
new obstacles into the area to force the planning of
more different trajectories. And finally we proposed
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
126

2 4 6 8 10 12 14 16
0.1
1
10
100
1000
10000
100000
Planning Time
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Voronoi-Delaunay - limit (100)
Number of Obstacles
Time [ms]
2 4 6 8 10 12 14 16
1
10
100
1000
10000
100000
Planning Time
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Voronoi-Delaunay - limit (100)
Number of Obstacles
Time [ms]
Figure 7: Time.
2 4 6 8 10 12 14 16
0
20
40
60
80
100
120
Number of Planned Alternatives
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Voronoi-Delaunay - limit (100)
Number of Obstacles
Number of Alternatives
2 4 6 8 10 12 14 16
0
20
40
60
80
100
120
Number of Planned Alternatives
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Voronoi-Delaunay - limit (100)
Number of Obstacles
Number of Alternatives
Figure 8: Number of alternatives.
2 4 6 8 10 12 14 16
0
5
10
15
20
25
30
Average Trajectory Length
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Trajectory Length
2 4 6 8 10 12 14 16
0
5
10
15
20
25
Average Trajectory Length
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Trajectory Length
Figure 9: Trajectory Length.
2 4 6 8 10 12 14 16
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Metric: Different States
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Different States
2 4 6 8 10 12 14 16
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Metric: Different States
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Different States
Figure 10: Different States.
PlanningofDiverseTrajectories
127
2 4 6 8 10 12 14 16
0
5
10
15
20
25
30
35
40
45
50
Metric: Trajectory Distance
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Trajectory Distance
2 4 6 8 10 12 14 16
0
5
10
15
20
25
30
Metric: Trajectory Distance
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Trajectory Distance
Figure 11: Trajectory Distance.
2 4 6 8 10 12 14 16
0
0.1
0.2
0.3
0.4
0.5
Metric: Obstacle Avoidance
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Obstacle Avoidance
2 4 6 8 10 12 14 16
0
0.1
0.2
0.3
0.4
0.5
Metric: Obstacle Avoidance
Different States Metric Planner
Trajectory Distance Metric
Trajectory MaxMin Distance
Metric Planner
Obstacle Extension - limit (100)
Obstacle Extension - limit (5)
Voronoi-Delaunay - limit (100)
Voronoi-Delaunay - limit (5)
Number of Obstacles
Obstacle Avoidance
Figure 12: Obstacle avoidance.
Figure 13: Example of trajectories generated by the Voronoi-Delaunay graph based diverse trajectory planner. In the left
figure we can see the shortest 5 trajectories and all 21 found trajectories are depicted in the right one.
two approaches which systematically extend the ob-
stacles and then use any traditional optimal trajectory
planner to find individual alternative trajectories. The
last approach, based on the Voronoi and the Delaunay
graphs, seems to be very promising both in the effec-
tiveness and in the ability to generate many alternative
trajectories. In the time critical scenarios a trajectory
metric based algorithm can be used.
So far, we focused on the 2D grid domains only,
which is often used for the trajectory planners com-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
128

parison. Nevertheless, all the presented algorithms
can be easily generalized to plan in the 3D space.
However, before we start with the deployment of
these methods to a human-machine interface, we need
to evaluate planned diverse trajectories on human op-
erators to choose the most suitable method. This will
form the major part of our future research.
REFERENCES
Aurenhammer, F. (1991). Voronoi diagrams – A survey of a
fundamental geometric data structure. ACM Computer
Survey, 23(3):345–405.
Coman, A. and Mu
˜
noz-Avila, H. (2011). Generating diverse
plans using quantitative and qualitative plan distance
metrics. In AAAI. AAAI Press.
Fikes, R. E. and Nilsson, N. J. (1971). Strips: A new ap-
proach to the application of theorem proving to prob-
lem solving. Artificial Intelligence, 2(3-4):189–208.
Fortune, S. (1997). Handbook of Discrete and Computa-
tional Geometry, chapter Voronoi diagrams and De-
launay triangulations, pages 377–388. CRC Press
LLC.
Garrido, S., Moreno, L., and Blanco, D. (2006). Voronoi di-
agram and fast marching applied to path planning. In
Proceedings of the 2006 IEEE International Confer-
ence on Robotics and Automation, ICRA 2006, pages
3049–3054. IEEE.
Hart, P., Nilsson, N., and Raphael, B. (1968). A formal
basis for the heuristic determination of minimum cost
paths. IEEE Transactions on Systems Science and Cy-
bernetics, (2):100–107.
Hui-ying, D., Shuo, D., and Yu, Z. (2010). Delaunay graph
based path planning method for mobile robot. In Com-
munications and Mobile Computing (CMC), 2010 In-
ternational Conference on, volume 3, pages 528–531.
Nash, A., Daniel, K., Koenig, S., and Felner, A. (2007).
Theta*: Any-angle path planning on grids. In Pro-
ceedings of the AAAI Conference on Artificial Intelli-
gence (AAAI), pages 1177–1183.
Yap, P. (2002). Grid-based path-finding. In Proceedings of
the Canadian Conference on Aritificial Intelligence,
pages 44–55.
PlanningofDiverseTrajectories
129
