
Rule-based Behavioral Reasoning on Semantic Business Processes
∗
Fabrizio Smith and Maurizio Proietti
CNR-IASI “Antonio Ruberti”, Viale Manzoni 30, 00185 Rome, Italy
Keywords:
Business Processes, Ontologies, Rule-based Reasoning, Verification.
Abstract:
We propose a rule-based framework for representing and reasoning about business processes from both the
procedural and ontological point of views. To this end we define a rule-based procedural semantics for a rel-
evant fragment of BPMN, a very popular graphical notation for specifying business processes. Our semantics
defines a state transition system by following an approach similar to the Fluent Calculus, and allows us to
specify state change in terms of preconditions and effects of the enactment of activities. Then we show how
the procedural process knowledge can be seamlessly integrated with the domain knowledge specified by using
the OWL-RL rule-based ontology language. Our framework provides a wide range of reasoning services by
using standard logic programming inference engines. In particular, we can perform very sophisticated rea-
soning tasks by combining both procedural and domain dependent knowledge. A preliminary implementation
shows that our approach is effective in practice.
1 INTRODUCTION
The adoption of structured and systematic approaches
for the management of the Business Processes (BPs)
operating within an organization is constantly gaining
popularity in various industrial sectors, especially in
medium to large enterprises, and in the public admin-
istration. The core of such approaches is the devel-
opment of BP models that represent the knowledge
about processes in machine accessible form. How-
ever, standard BP modeling languages are not fully
adequate to capture process knowledge in all its as-
pects. While their focus is on the procedural repre-
sentation of a BP as a workflow graph that specifies
the planned order of operations, the domain knowl-
edge regarding the entities involved in such a process,
i.e., the business environment in which processes are
carried out, is mainly left implicit. This kind of
knowledge is typically expressed through natural lan-
guage comments and labels attached to the models,
which constitute very limited, informal and ambigu-
ous pieces of information.
The above issues are widely recognized as an ob-
stacle for the further automation of BP Management
(BPM) tools and methodologies (Hepp et al., 2005).
Process modeling, in particular, is still mainly a man-
ual activity, where a very limited support is given in
∗
This work has been partly funded by the European
Commission through the ICT Project BIVEE: Business In-
novation and Virtual Enterprise Environment (No. FoF-
ICT-2011.7.3-285746).
terms of reuse and retrieval functionalities, or auto-
mated analysis facilities, i.e., for verifying whether
the requirements specified over the models are en-
forced. The latter aspect is addressed in the BPM
community mainly from a control flow perspective
(ter Hofstede et al., 2010), with the aim of verifying
whether the behavior of the modeled system presents
logical errors (see, for instance, the notion of sound-
ness (van der Aalst, 1998)).
However, in order to verify that a BP actually
behaves as expected, additional domain knowledge
is required. In this respect, the application of well-
established techniques stemming from the area of
Knowledge Representation in the domains of BP
modeling (Hepp et al., 2005; Lin, 2008; Weber et al.,
2010) and Web Services (Burstein et al., 2004; Fensel
et al., 2006) has been shown as a promising approach.
In particular, the use of computational ontologies is
the most established approach for representing in a
machine processable way the knowledge about the
domain where business processes operate, providing
formal definitions for the basic entities involved in
a process, such as activities, actors, data items, and
the relations between them. However, there are still
several open issues regarding the combination of BP
modeling languages (with their execution semantics)
and ontologies, and the accomplishment of behavioral
reasoning tasks involving both these components.
The main objective of this paper is to design a
framework for representing and reasoning about busi-
ness process knowledge from both the procedural and
130
Smith F. and Proietti M..
Rule-based Behavioral Reasoning on Semantic Business Processes.
DOI: 10.5220/0004255001300143
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 130-143
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

ontological point of views. To achieve this goal, we
do not propose yet another business process modeling
language, but we provide a rule-based framework for
reasoning about process-related knowledge expressed
by using de-facto standards for BP modeling, like
BPMN (OMG, 2011), and ontology definition, like
OWL (Hitzler et al., 2009). To this end we define a
rule-based procedural semantics for a relevant frag-
ment of BPMN, and we extend it in order to take into
account OWL annotations that describe preconditions
and effects of activities and events occurring within
a BP. Our procedural BP semantics seamlessly inte-
grates with OWL-RL (Hitzler et al., 2009), a fragment
of the OWL ontology language which has a suitable
rule-based presentation, and is achieving increasing
success because it constitutes an excellent compro-
mise between expressivity and efficiency.
In essence, the contributions of this paper can be
summarized as follows. In Section 2 we introduce a
set of rules, expressed in the logic programming for-
malism (Lloyd, 1987), for modeling the procedural
semantics of a BP regarded as a workflow. The pro-
posed rule set can cope with a relevant fragment of
the BPMN 2.0 specification, allowing us to deal with
a large class of process models. We then propose in
Section 3 an approach for the semantic annotation of
BP models, where preconditions and effects of BP el-
ements are described by using an OWL-RL ontology.
In Section 4 we provide a general verification mech-
anism by encoding the temporal logic CTL (Clarke
et al., 1999) as a set of rules which allow us to ana-
lyze properties of BPs depending on both the control
flow and semantic annotations. Finally, in Section
5 we show how we can perform some very sophis-
ticated reasoning tasks, such as verification, querying
and trace compliance checking, that combine both the
procedural and domain knowledge relative to a BP.
2 BEHAVIORAL SEMANTICS OF
BP SCHEMAS
In this section we introduce a formal representation
of business processes by means of the notion of Busi-
ness Process Schema (BPS). A BPS, its meta-model,
and its procedural (or behavioral) semantics will all
be specified by sets of rules, for which we adopt the
standard notation and semantics of logic program-
ming (see, for instance, (Lloyd, 1987)). In particular,
a rule is of the form A ← L
1
∧ . . . ∧ L
n
, where A is
an atom (i.e., a formula of the form p(t
1
, . . . ,t
m
)) and
L
1
, . . . , L
n
are literals (i.e., atoms or negated atoms).
If n = 0 we call the rule a fact. A rule (atom, lit-
eral) is ground if no variables occur in it. A logic
program is a finite set of rules. Throughout the paper
we will consider the class of (locally) stratified logic
programs, where no ground atom depends negatively
on itself. For every program P in this class there ex-
ists a unique perfect model, denoted Perf(P), defined
as shown in (Przymusinski, 1988).
2.1 Business Process Schemas
We show how a BPS is specified by means of an ex-
ample. The full definition can be found in (Smith
et al., 2012). Let us consider the BP depicted in Fig-
ure 1, where the handling of a purchase order is rep-
resented using the BPMN notation. The process starts
with the ordering activity, which is a compound activ-
ity where, upon receiving a customer request, a pur-
chase order is created (create order), approved (ac-
cept order) or canceled (cancel order). An approved
order can also be subjected to a number of modifi-
cations (modify order). If the order is canceled, the
rejection is notified to the customer and the order is
archived (notify rejection). Otherwise, after the req-
uisition of the requested items (parts auction and al-
locate inventory), the delivery of products takes place
together with the payment of the order (fulfill order).
A BPS (e.g., Handle Order) consists of a set of
flow elements and relations between them, and it is
associated with a unique start event and a unique end
event, which are flow elements that represent the entry
point and the exit point, respectively, of the process.
An activity is a flow element that represents a unit
of work performed within the process. A task repre-
sents an atomic activity (e.g., accept order), i.e., no
further decomposable, while a compound activity is
associated with a process that provides the definition
of its internal structure (e.g., ordering). An interme-
diate event represents “something that occurs during
the process execution” (e.g., the time-out exception
attached to the accept order activity). The sequenc-
ing of flow elements is specified by the sequence
flow relation (corresponding to solid arrows), and the
branching/merging of the control flow is specified by
using three types of gateways: exclusive (XOR, e.g.,
g1), inclusive (OR, e.g., g3), and parallel (AND, not
exemplified in Figure 1). The item flow relation (cor-
responding to dotted arrows) specifies that a flow el-
ement uses as input (e.g., accept order and order)
or produces as output (e.g., create order and order) a
particular item, i.e., a physical or information object.
A BPS can also represent other entities usually
employed to model business processes, such as par-
ticipants and messages, not presented here for lack
of space. Indeed, by following our approach we can
represent the constructs common to the most used BP
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
131
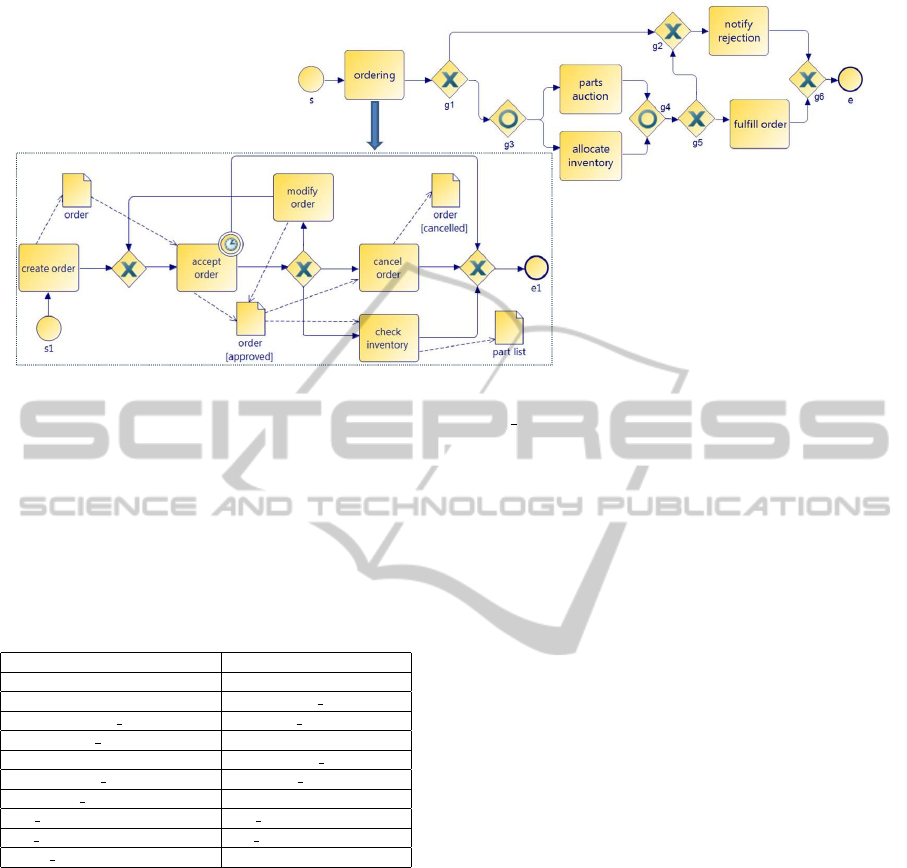
Figure 1: Handle Order BP.
modeling languages and, in particular, the ones based
on the BPMN 2.0 specification (OMG, 2011).
Formally, a BPS is specified by a set of ground
facts of the form p(c
1
, . . . , c
n
), where c
1
, . . . , c
n
are
constants denoting flow elements (e.g., activities,
events, and gateways) and p is a predicate symbol. An
excerpt of the translation of the Handle Order process
(referred to as ho) as a BPS is shown in Table 1.
Table 1: BPS representing the Handle Order process.
bp(ho,s,e) seq(s, ordering, ho)
seq(ordering,g1,ho) seq(g1,g2, ho)
seq(g1,g3,ho) seq(g3,parts auction,ho)
seq(g3,allocate inventory,ho) seq(parts auction,g4,ho)
seq(allocate inventory,g4,ho) seq(g4,g5,ho)
seq(g5,g2,ho) seq(g5,fulfill order,ho)
seq(g2,notify rejection,ho) seq(fulfill order,g6,ho)
seq(notify rejection,g6,ho) seq(g6,e,ho)
exc branch(g1) exc merge(g2)
inc branch(g3) inc merge(g4)
comp act(ordering, s
1
, e
1
) . . .
Our formalization also includes a set of rules that
represent the meta-model, defining a number of struc-
tural properties which regard a BPS as a directed
graph, where edges correspond to sequence and item
flow relations. Two categories of structural proper-
ties should be verified by a well-formed (i.e., syn-
tactically correct) BPS: i) local properties related to
its elementary components (e.g., every activity must
have at most one ingoing and at most one outgoing
sequence flow), and ii) global properties related to the
overall structure of the BPS (e.g., every flow element
must lie on a path from the start to the end event).
Furthermore, other meta-model properties are re-
lated to the notions of path and reachability between
flow elements, such as the following ones, which will
be used in the sequel: seq
+
(E
1
, E
2
, P), representing
the transitive closure of the sequence flow relation,
and n reachable(E
1
, E
2
, E
3
, P), which holds if there
is a path in P between E
1
and E
2
not including E
3
.
2.2 Behavioral Semantics
Now we present a formal definition of the behav-
ioral semantics, or enactment, of a BPS, by fol-
lowing an approach inspired to the Fluent Calcu-
lus, a well-known calculus for action and change
(see (Thielscher, 1998) for an introduction). In the
Fluent Calculus, the state of the world is represented
as a collection of fluents, i.e., terms representing
atomic properties that hold at a given instant of time.
An action, also represented as a term, may cause
a change of state, i.e., an update of the collection of
fluents associated with it. Finally, a plan is a sequence
of actions that leads from the initial to the final state.
For states we use set notation (here we de-
part from (Thielscher, 1998), where an associative-
commutative operator is used for representing col-
lections of fluents). A fluent is an expression of the
form f (a
1
, . . . , a
n
), where f is a fluent symbol and
a
1
, . . . , a
n
are constants or variables. In order to model
the behavior of a BPS, we represent states as finite
sets of ground fluents. We take a closed-world inter-
pretation of states, that is, we assume that a fluent F
holds in a state S iff F ∈ S. This set-based representa-
tion of states relies on the assumption that the BPS is
safe, i.e., during its enactment there are no concurrent
executions of the same flow element (van der Aalst,
1998). This assumption enforces that the set of states
reachable by a given BPS is finite.
A fluent expression is built inductively from flu-
ents, the binary function symbol and, and the unary
function symbol not. The satisfaction relation as-
signs a truth value to a fluent expression with respect
to a state. This relation is encoded by a predicate
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
132

holds(F, S), which holds if the fluent expression F
is true in the state S. We also introduce a constant
symbol true, such that holds(true, S) holds for every
state S. Accordingly to the closed-world interpreta-
tion given to states, the satisfaction relation is defined
by the following rules:
holds(F, S) ← F = true
holds(F, S) ← F ∈ S
holds(not(F), S) ← ¬holds(F, S)
holds(and(F
1
, F
2
), S) ← holds(F
1
, S) ∧ holds(F
2
, S)
We will consider the following two kinds of fluents:
• cf(E
1
, E
2
, P), which means that the flow element
E
1
has been executed and the flow element E
2
is
waiting for execution, during the enactment of the
process P (cf stands for control flow);
• en(A, P), which means that the activity A is being
executed during the enactment of the process P
(en stands for enacting).
To clarify our terminology note that, when a flow el-
ement E
2
is waiting for execution, E
2
might not be
enabled to execute, because other conditions need to
be fulfilled, such as those depending on the synchro-
nization with other flow elements (see, in particular,
the semantics of merging behaviors below).
We assume that the execution of an activity has a
beginning and a completion (although we do not as-
sociate a duration with activity execution), while the
other flow elements execute instantaneously. Thus,
we will consider two kinds of actions: begin(A) which
starts the execution of an activity A, and complete(E),
which represents the completion of the execution of a
flow element E (possibly, an activity). The change of
state determined by the execution of an action will
be formalized by a relation result(S
1
, A, S
2
), which
holds if the action A can be executed in the state
S
1
leading to the state S
2
. For defining the rela-
tion result(S
1
, A, S
2
) the following auxiliary predi-
cates will be used: (i) update(S
1
, T,U, S
2
), which
holds if S
2
= (S
1
− T ) ∪U, where S
1
, T,U, and S
2
are
sets of fluents, and (ii) setof(F,C, S), which holds if
S is the set of ground instances of fluent F such that
condition C holds.
The relation r(S
1
, S
2
) holds if a state S
2
is imme-
diately reachable from a state S
1
, that is, some action
A can be executed in state S
1
leading to state S
2
:
r(S
1
, S
2
) ← result(S
1
, A, S
2
)
We say that a state S
2
is reachable from a state S
1
if
there is a finite sequence of actions (of length ≥ 0)
from S
1
to S
2
, that is, reachable
state(S
1
, S
2
) holds,
where the relation reachable state is is the reflexive-
transitive closure of r
In the rest of this section we present a fluent-based
formalization of the behavioral semantics of a BPS by
focusing on a core of the BPMN language. The pro-
posed formal semantics mainly refers to the BPMN
semantics, as described (informally) in the most re-
cent specification of the language (OMG, 2011).
Most of the constructs considered here (e.g., paral-
lel or exclusive branching/merging) have the same in-
terpretation in most workflow languages. However,
when different interpretations are given, e.g., in the
case of inclusive merge, we stick to the BPMN one.
2.2.1 Activity and Event Execution
The enactment of a process P begins with the execu-
tion of the associated start event E in a state where the
fluent cf(start, E, P) holds, being start a reserved con-
stant. After the execution of the start event, its unique
successor waits for execution.
result(S
1
, complete(E), S
2
) ← start
event(E) ∧
holds(cf(start, E, P), S
1
) ∧ seq(E, X, P) ∧
update(S
1
, {cf(start, E, P)}, {cf(E, X, P)}, S
2
)
The execution of an end event leads to the final
state of a process execution, in which the fluent
cf(E, end, P) holds, where E is the end event associ-
ated with the process P and end is a reserved constant.
result(S
1
, complete(E), S
2
) ←
end event(E) ∧ holds(cf(X, E, P), S
1
) ∧
update(S
1
, {cf(X, E, P)}, {cf(E, end, P)}, S
2
)
The execution of an activity is enabled to begin af-
ter the completion of its unique predecessor flow ele-
ment. The effects of the execution of an activity vary
depending on its type (i.e., atomic task or compound
activity). The beginning of an atomic task A is mod-
eled by adding the en(A, P) fluent to the state. At
the completion of A, the en(A, P) fluent is removed
and the control flow moves on to the unique succes-
sor of A.
result(S
1
, begin(A), S
2
) ← task(A) ∧
holds(cf(X, A, P), S
1
) ∧
update(S
1
, {cf(X, A, P)}, {en(A, P)}, S
2
)
result(S
1
, complete(A), S
2
) ← task(A) ∧
holds(en(A, P), S
1
) ∧ seq(A,Y, P) ∧
update(S
1
, {en(A, P)}, {cf(A,Y, P)}, S
2
)
The execution of a compound activity, whose internal
structure is defined as a process itself, begins by en-
abling the execution of the associated start event, and
completes after the execution of the associated end
event.
result(S
1
, begin(A), S
2
) ← comp act(A,S, E) ∧
holds(and(cf(X , A, P), not(en(A, P))), S
1
) ∧
update(S
1
, {cf(X, A, P)}, {cf(start, S, A), en(A, P)}, S
2
)
result(S
1
, complete(A), S
2
) ← comp act(A, S, E) ∧
holds(and(cf(E, end, A), en(A, P)), S
1
) ∧
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
133

seq(A,Y, P) ∧ update(S
1
, {en(A, P), cf(E, end, A)},
{cf(A,Y, P)}, S
2
)
According to the informal semantics of BPMN, inter-
mediate events are intended as instantaneous patterns
of behavior that are registered at a given time point.
Thus, we formally model the execution of an inter-
mediate event as a single state transition, as follows:
result(S
1
, complete(E), S
2
) ← int event(E) ∧
holds(cf(X, E, P), S
1
) ∧ seq(E,Y, P) ∧
update(S
1
, {cf(X, E, P)}, {cf(E,Y, P)}, S
2
)
Intermediate events in BPMN can also be attached to
activity boundaries to model exceptional flows. Upon
occurrence of an exception, the execution of the ac-
tivity is interrupted, and the control flow moves along
the sequence flow that leaves the event:
result(S
1
, complete(E), S
2
) ← exception(E, A, P) ∧
int event(E) ∧ holds(en(A, P), S
1
) ∧ seq(E,Y, P) ∧
update(S
1
, {en(A, P)}, {cf(E,Y, P)}, S
2
)
2.2.2 Branching Behaviors
When a branch gateway is executed, a subset of its
successors is selected for execution. We consider here
exclusive, inclusive, and parallel branch gateways.
An exclusive branch leads to the execution of ex-
actly one successor, while an inclusive branch leads
to the concurrent execution of a non-empty subset of
its successors. The set of successors of exclusive or
inclusive decision points is selected by using guards,
i.e., fluent expressions whose truth value is tested
with respect to the current state. The value of guards
may depend on fluents different from cf(E
1
, E
2
, P)
and en(A, P). Indeed, extra fluents can be introduced
for modeling the effects of the execution of flow el-
ements (e.g., operations on items) as shown in Sec-
tion 3.2. A guard is associated with a gateway by the
predicate c seq(G, B,Y, P) modeling a conditional se-
quence flow, where G is a fluent expression denot-
ing a guard, B is an exclusive or inclusive branch
gateway and Y is a successor flow element of B in
the process P. We also have the rule seq(B,Y, P) ←
c seq(G,B,Y, P). The semantics of inclusive branches
is defined as follows:
result(S
1
, complete(B), S
2
) ← inc branch(B) ∧
holds(cf(X, B, P), S
1
)∧ setof(cf(B,Y, P),
(c seq(G, B,Y, P) ∧ holds(G, S
1
)), Succ)∧
update(I, {cf(X , B, P)}, Succ, S
2
)
The semantics of exclusive branches can be defined in
a similar way and is omitted. Finally, a parallel branch
leads to the concurrent execution of all its successors,
that is:
result(S
1
, complete(B), S
2
) ← par branch(B) ∧
holds(cf(X, B, P), S
1
) ∧
setof(cf(B,Y, P), seq(B,Y, P), Succ)∧
update(S
1
, {cf(X, B, P)}, Succ, S
2
)
2.2.3 Merging Behaviors
An exclusive merge can be executed whenever at least
one of its predecessors has been executed. Here we
omit the straightforward formal definition.
For the inclusive merge several operational se-
mantics have been proposed, due to the complexity of
its non-local semantics, see e.g., (Kindler, 2006). An
inclusive merge is supposed to be able to synchronize
a varying number of threads, i.e., it is executed only
when n(≥ 1) predecessors have been executed and no
other will be eventually executed. Here we refer to
the semantics described in (V
¨
olzer, 2010) adopted by
BPMN, stating that an inclusive merge M can be exe-
cuted if the following two conditions hold:
(1) at least one of its predecessors has been executed,
(2) for each non-executed predecessor X, there is no
flow element U which is waiting for execution and
is upstream X. The notion of being upstream cap-
tures the fact that U may lead to the execution of
X, and is defined as follows. A flow element U is
upstream X if:
(a) there is a path from U to X not including M, and
(b) there is no path from U to an executed prede-
cessor of M that does not include M.
This semantics is formalized as follows:
result(S
1
, complete(M), S
2
) ← inc merge(M) ∧
enabled im(M, S
1
, P) ∧ seq(M,Y, P) ∧
setof(cf(X, M, P), holds(cf(X, M, P), S
1
), PredM) ∧
update(S
1
, PredM, {cf(M,Y, P)}, S
2
)
where enabled im is a predicate encoding Conditions
(1) and (2) above, that is:
enabled im(M, S
1
, P) ← holds(cf(X, M, P), S
1
) ∧
¬exists upstream(M, S
1
, P)
exists upstream(M, S
1
, P) ← seq(X, M, P) ∧
holds(not(cf(X, M, P)), S
1
) ∧
holds(cf(Y,U, P), S
1
) ∧ upstream(U, X, M, S
1
, P)
upstream(U, X, M, S
1
, P) ←
n reachable(U, X, M, P) ∧
¬exists path(U, M, S
1
, P)
exists path(U, M, S
1
, P) ← holds(cf(K, M, P), S
1
) ∧
n reachable(U, K, M, P)
Finally, a parallel merge can be executed if all its pre-
decessors have been executed:
result(S
1
, complete(M), S
2
) ← par merge(M) ∧
¬exists non executed pred(M, P, S
1
)∧seq(M,Y, P)∧
setof(cf(X, M, P), seq(X, M, P), PredM) ∧
update(S
1
, PredM, {cf(M,Y, P)}, S
2
)
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
134

where exists non executed pred(M, P, S
1
) holds if
there exists no predecessor of M which has not been
executed in state S
1
, that is:
exists non executed pred(M, P, S
1
) ←
seq(X, M, P) ∧ holds(not(cf(X, M, P)), S
1
)
3 SEMANTIC ANNOTATION
In the previous section we have shown how the behav-
ioral semantics of the workflow specified by a BPS
can be modeled in our rule-based framework. How-
ever, not all the relevant knowledge regarding process
enactment is captured by a workflow model, which
defines the planned order of operations but does
not provide an explicit representation of the domain
knowledge regarding the entities involved in such a
process, i.e., the business environment in which pro-
cesses are carried out.
Similarly to proposals like Semantic BPM (Hepp
et al., 2005) and Semantic Web Services (Fensel et al.,
2006), we will make use of semantic annotations to
enrich the procedural knowledge specified by a BPS
with domain knowledge expressed in terms of a given
business reference ontology. Annotations provide two
kinds of ontology-based information: (i) formal defi-
nitions of the basic entities involved in a process (e.g.,
activities, actors, items) to specify their meaning in an
unambiguous way (terminological annotations), and
(ii) specifications of preconditions and effects of the
enactment of flow elements (functional annotations).
In this work we focus on functional annotations
and on their interaction with the control flow to define
the behavior of a BPS, thus extending the framework
presented in (Smith et al., 2012) where terminological
annotations only were considered.
3.1 Rule-based Ontologies
A business reference ontology is intended to cap-
ture the semantics of a business scenario in terms of
the relevant vocabulary plus a set of axioms (TBox)
which define the intended meaning of the vocabulary
terms. In order to represent the semantic annotations
and the behavioral semantics of a BPS in a uniform
way, we will represent ontologies by sets of rules.
To this end, we consider a fragment of OWL falling
within the OWL 2 RL (Hitzler et al., 2009) profile,
which is an upward-compatible extension of RDF and
RDFS whose semantics is defined via a set of Horn
rules, called OWL 2 RL/RDF rules. OWL 2 RL on-
tologies are modeled by means of the ternary pred-
icate t(s, p, o) representing an OWL statement with
subject s, predicate p and object o. For instance, the
assertion t(a, rdfs:subClassOf,b) represents the inclu-
sion axiom a v b. Reasoning on triples is supported
by OWL 2 RL/RDF rules of the form t(s, p, o) ←
t(s
1
, p
1
, o
1
) ∧ · ·· ∧ t(s
n
, p
n
, o
n
). For instance, the rule
t(A, rdfs:subClassOf,B) ← t(A, rdfs:subClassOf,C) ∧
t(C, rdfs:subClassOf, B) defines the transitive closure
of the subsumption relation.
An OWL 2 RL ontology is represented as a set
O of rules, consisting of a set of facts of the form
t(s, p, o), called triples, encoding the OWL TBox and
the set of Horn rules encoding the OWL 2 RL/RDF
rules. This kind of representation allows us to take
advantage of the efficient resolution strategies devel-
oped for logic programs, in order to perform the rea-
soning tasks typically supported by Description Log-
ics reasoning systems, such as concept subsumption
and ontology consistency.
Table 2: Business Reference Ontology excerpt.
ClosedPO v Order ApprovedPO v Order
CancelledPO v ClosedPO FulfilledPO v ClosedPO
UnavailablePL v PartList AvailablePL v PartList
payment v related ∃ payment
−
v Invoice
ApprovedPO u∃related.Invoice v FulfilledPO
Order u∃related.UnavailablePL v CancelledPO
CancelledPO u ApprovedPO v ⊥
UnavailablePL u AvailablePL v ⊥
3.2 Functional Annotation
By using the ontology vocabulary and axioms, we de-
fine semantic annotations for modeling the behavior
of individual process elements in terms of precon-
ditions under which a flow element can be executed
and effects on the state of the world after its execu-
tion. Preconditions and effects, collectively called
functional annotations, can be used, for instance, to
model input/output relations of activities with data
items, which are the standard way of representing in-
formation storage in BPMN diagrams. Fluents can
represent the status of a data item affected by the exe-
cution of an activity at a given time during the execu-
tion of the process. A precondition specifies the status
a data item must posses when an activity is enabled to
start, and an effect specifies the status of a data item
after having completed an activity. In order to provide
concrete examples to illustrate the main ideas, in the
rest of the paper we refer to the excerpt of reference
ontology reported in Table 2, describing the items in-
volved in the BPS depicted in Figure 1.
Functional annotations are formulated by means
of the following two relations:
• pre(A,C, P), which specifies the fluent expression
C, called enabling condition, which must hold to
execute an element A in the process P;
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
135

• eff(A, E
−
, E
+
, P), which specifies the set E
−
of
fluents, called negative effects, which do not hold
after the execution of A and the set of fluents E
+
,
called positive effects, which hold after the execu-
tion of A in the process P. We assume that E
−
and
E
+
are disjoint sets.
In the presence of functional annotations, the enact-
ment of a BPS is modeled as follows. Given a state
S
1
, a flow element A can be enacted if A is wait-
ing for execution according to the control flow se-
mantics, and its enabling condition C is satisfied, i.e.,
holds(C, S
1
) is true. Moreover, given an annotation
eff(A,E
−
, E
+
, P), when A is completed in a given
state S
1
, then a new state S
2
is obtained by taking out
from S
1
the set E
−
of fluents and then adding the set
E
+
of fluents. We will assume that effects satisfy a
consistency condition which guarantees that: (i) no
contradiction can be derived from the fluents of S
2
by
using the state independent axioms of the reference
ontology, and (ii) no fluent belonging to E
−
holds in
S
2
. This consistency condition will be formally de-
fined later in this section, and can be regarded as a
way of tackling the Ramification Problem due to in-
direct effects of actions (see e.g., (Thielscher, 1998;
Reiter, 2001)).
The state update is formalized by extending the
result relation so as to take into account the pre and eff
relations. We only consider the case of task execution.
The other cases are similar and will be omitted.
result(S
1
, begin(A), S
2
) ← task(A)∧
holds(cf(X, A, P), S
1
)∧pre(A,C, P)∧holds(C, S
1
)∧
update(S
1
, {cf(X, A, P)}, {en(A, P)}, S
2
)
result(S
1
, complete(A), S
2
) ← task(A)∧
holds(en(A, P), S
1
) ∧ eff(A, E
−
, E
+
, P)∧
seq(A,Y, P) ∧ update(S
1
, {en(A, P)} ∪ E
−
,
{cf(A,Y, P)} ∪ E
+
, S
2
)
The enabling conditions and the negative and positive
effects occurring in functional annotations are fluent
expressions built from fluents of the form t
f
(s, p, o),
corresponding to the OWL statement t(s, p, o), where
we adopt the usual rdf, rdfs, and owl prefixes for
names in the OWL vocabulary, and the bro prefix for
names relative to our specific examples. We assume
that the fluents appearing in functional annotations are
either of the form t
f
(a, rdf:type, c), corresponding to
the unary atom c(a), or of the form t
f
(a, p, b), cor-
responding to the binary atom p(a, b), where a and
c are individuals, while c and p are concepts and
properties, respectively, defined in the reference on-
tology O. Thus, fluents correspond to assertions about
individuals, i.e., the ABox of the ontology, and hence
the ABox may change during process enactment due
to the effects specified by the functional annotations,
while O, providing the ontology definitions and ax-
ioms, i.e., the TBox of the ontology, does not change.
Let us now present an example of specification
of functional annotations. In particular, our example
shows nondeterministic effects, that is, a case where a
flow element A is associated with more than one pair
(E
−
, E
+
) of negative and positive effects.
Example 1. Consider again the Handle Order pro-
cess in Figure 1. After the execution of create order, a
purchase order is issued. This order can be approved
or canceled upon execution of the activities accept
order and cancel order, respectively. Depending on
the inventory capacity checked during the check in-
ventory task, the requisition of parts performed by an
external supplier is performed (parts auction). Once
that all the order parts are available, the order can be
fulfilled and an invoice is associated with the order.
This behavior is specified by the functional annota-
tions reported in Table 3.
In order to evaluate a statement of the form
holds(t
f
(s, p, o), X), where t
f
(s, p, o) is a fluent and X
is a state, the definition of the holds predicate given
previously must be extended to take into account the
axioms belonging to the reference ontology O. In-
deed, we want that a fluent of the form t
f
(s, p, o) be
true in state X not only if it belongs to X, but also if
it can be inferred from the fluents in X and the ax-
ioms of the ontology. For instance, let us consider
the fluent F = t
f
(o, rdf:type, bro:CancelledPO). We
can easily infer that F holds in a state which con-
tains {t
f
(o, rdf:type, bro:CancelledPO)} (e.g., reach-
able after the execution of cancel order) by
using the rule holds(F, X) ← F ∈ X . How-
ever, by taking into account the ontology ex-
cerpt given in Table 2, we also want to be
able to infer that F holds in a state which con-
tains {t
f
(o, rdf:type, bro:Order), t
f
(o, bro:related, pl),
t
f
(pl, rdf:type, bro:UnavailablePL)} (e.g., reachable
after the execution of parts auction).
In our framework the inference of new fluents
from fluents belonging to states is performed by using
extra rules obtained by translating part of the OWL 2
RL/RDF entailment rules into rules for inferring holds
atoms. These extra rules are derived by replacing ev-
ery OWL triple of the form t(s, p, o), where s refers
to an individual, by the atom holds(t
f
(s, p, o), X). Be-
low we show the derived rules for concept subsump-
tion (1), role subsumption (2), domain restriction (3),
transitive property (4), and concept disjointness (5) .
1. holds(t
f
(S, rdf:type,C), X) ←
holds(t
f
(S, rdf:type, B), X) ∧
t(B, rdfs:subClassOf,C)
2. holds(t
f
(S, P, O), X) ← holds(t
f
(S, P1, O), X) ∧
t(P1, rdfs:subPropertyOf, P)
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
136

Table 3: Functional annotations for the Handle Order process.
Flow Element Enabling Condition Negative Effects Positive Effects
create order t
f
(o, rdf:type, bro:Order)
accept order t
f
(o, rdf:type, bro:Order) t
f
(o, rdf:type, bro:ApprovedPO)
cancel order t
f
(o, rdf:type, bro:ApprovedPO) t
f
(o, rdf:type, bro:ApprovedPO) t
f
(o, rdf:type, bro:CancelledPO)
check inventory t
f
(o, rdf:type, bro:ApprovedPO) t
f
(o, bro:related, pl)
t
f
(pl, rdf:type, bro:PartList)
check inventory t
f
(o, rdf:type, bro:ApprovedPO)
parts auction t
f
(pl, rdf:type, bro:PartList) t
f
(pl, rdf:type, bro:AvailablePL)
parts auction t
f
(pl, rdf:type, bro:PartList) t
f
(o, rdf:type, bro:ApprovedPO) t
f
(pl, rdf:type, bro:UnavailablePL)
fulfill order t
f
(o, rdf:type, bro:ApprovedPO) t
f
(o, bro:payment,i)
Gateway Target Guard
g1 g3 t
f
(o, rdf:type, bro:ApprovedPO)
g1 g2 not(t
f
(o, rdf:type, bro:ApprovedPO))
g3 parts auction and(t
f
(o, related, pl), t
f
(pl, rdf:type, bro:PartList))
g5 g2 t
f
(o, rdf:type, bro:CancelledPO)
g5 fulfill order not(t
f
(o, rdf:type, bro:CancelledPO))
3. holds(t
f
(S, rdf:type,C), X) ←
holds(t
f
(S, P, O), X) ∧t(P, rdfs:domain,C)
4. holds(t
f
(S, P, O), X) ←
holds(t
f
(S, P, O
1
), X) ∧ holds(t
f
(O
1
, P, O), X ) ∧
t(P, rdf:type, owl:TransitiveProperty)
5. holds(false, X ) ← holds(t
f
(I
1
, rdf:type, A), X) ∧
holds(t
f
(I
2
, rdf:type, B), X) ∧
t(A, owl:disjointWith, B)
We denote by F the set of rules that encode the func-
tional annotations, that is, the facts defining the re-
lations pre(A,C, P) and eff(A, E
−
, E
+
, P), along with
the rules for evaluating holds(t
f
(s, p, o), X) atoms
(such as rules 1–5 above).
The rules in O ∪F may also be needed to evaluate
atoms of the form holds(G, X) in the case where G is
a guard expression associated with inclusive or exclu-
sive branch points via the relation c seq(G, B,Y, P).
Indeed, G may depend on fluents introduced by func-
tional annotations.
We are now able to define the consistency condi-
tion for effects in a rigorous way. We say that eff is
consistent with process P if, for every flow element A
and states S
1
, S
2
, the following implication is true:
If the state S
1
is reachable from the initial state of P,
the relation result(S
1
, complete(A), S
2
) holds, and the
relation eff(A,E
−
, E
+
, P) holds,
Then O ∪ F ∪ {¬holds(false, S
2
)} is consistent And
for all F ∈ E
−
, O ∪F ∪{¬holds(F, S
2
)} is consistent.
We will show in Section 5 how the consistency of
effects can be checked by using the rule-based tempo-
ral logic we will present in the next section.
4 TEMPORAL REASONING
In order to provide a general verification mechanism
for behavioral properties, in this section we propose
a model checking methodology based on a formal-
ization of the temporal logic CTL (Computation Tree
Logic, see (Clarke et al., 1999) for a comprehensive
overview) as a set of rules. Model checking is a
widely accepted technique for the formal verification
of BP schemas, as their execution semantics is usu-
ally defined in terms of states and state transitions,
and hence the use of temporal logics for the specifi-
cation and verification of properties is a very natural
choice (Fu et al., 2004; Liu et al., 2007).
CTL is a propositional temporal logic introduced
for reasoning about the behavior of reactive systems.
The behavior is represented as the tree of states that
the system can reach, and each path of this tree is
called a computation path. CTL formulas are built
from: the constants true and false; a given set Elem
of elementary properties; the connectives: ¬ (‘not’)
and ∧ (‘and’); the linear-time operators along a com-
putation path: G (‘globally’ or ‘always’), F (‘finally’
or ‘sometimes’), X (‘next-time’), and U (‘until’); the
quantifiers over computation paths: A (‘for all paths’)
and E (‘for some path’). The abstract syntax of CTL
is defined as follows.
Definition 1 (CTL formulas). Let Elem be a given
set of elementary properties. A CTL formula F has
the following syntax:
F ::= e | true | false | ¬F | F
1
∧ F
2
|
EX(F) | EU(F
1
, F
2
) | EG(F)
where e belongs to Elem.
Other operators can be defined in terms of the ones
given in Definition 1, e.g., EF(F) ≡ EU(true, F) and
AG(F) ≡ ¬EF(¬F) (Clarke et al., 1999).
Usually, the semantics of CTL formulas is defined
by introducing a Kripke structure K , which repre-
sents the state space and the state transition relation,
and by defining the satisfaction relation K ,s |= F,
which denotes that a formula F holds in a state s of
K (Clarke et al., 1999).
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
137

In order to verify temporal properties of the be-
havior of a BPS P, we define a Kripke structure as-
sociated with P. The states are defined as finite sets
of ground fluents and the state transition relation is
based on the immediate reachability relation r be-
tween states defined in Section 2.2. The Kripke struc-
ture and the satisfaction relation will be encoded by
sets of rules, hence providing a uniform framework
for reasoning about the ontological properties and the
behavioral properties of business processes.
A Kripke structure is a four-tuple K =
hS, I , R , Li defined as follows.
1. S is the finite set of all states, where a state is a
finite set of ground fluents.
2. I is the initial state of BPS P, encoded by the rule:
initial(I, P) ← bp(P, S, E) ∧ I = {cf(start, S, P)}
3. R is the transition relation, which is defined as
follows: R (X,Y ) holds iff r(X,Y ) holds, where
r is the predicate defined in Section 2.2, i.e.,
R (X,Y ) holds iff there exists an action A that can
be executed in state X leading to state Y .
4. L is the labeling function, which associates with
each state X the set of fluents F such that O ∪F |=
holds(F, X).
In the definition of Kripke structure given in (Clarke
et al., 1999), the transition relation R is assumed to
be total, that is, every state S
1
has at least one suc-
cessor state S
2
for which R (S
1
, S
2
) holds. This as-
sumption is justified by the fact that reactive systems
can be thought as ever running processes. However,
this assumption is not realistic in the case of busi-
ness processes, for which there is always at least one
state with no successors, namely one where the end
event of a BPS has been completed. For this rea-
son the semantics of the temporal operators given in
(Clarke et al., 1999), which refers to infinite paths of
the Kripke structure, is suitably changed here by tak-
ing into consideration maximal paths, i.e., paths that
are either infinite or end with a state that has no suc-
cessors, called a sink.
Definition 2 (Maximal Path). A maximal path in K
starting from a state S
0
is either
• an infinite sequence of states S
0
S
1
. . . such that
S
i
R S
i+1
, for every i≥ 0; or
• a finite sequence of states S
0
S
1
. . . S
k
, with k ≥ 0,
such that:
1. S
i
R S
i+1
, for every 0 ≤ i < k, and
2. there exists no state S
k+1
∈ S such that
S
k
R S
k+1
.
The semantics of CTL operators can be encoded by
extending the definition of the predicate holds. Be-
low we list the semantics of those operators and the
corresponding rule-based formalization.
EX(F) holds in state S
0
if F holds in a successor state
of S
0
:
holds(ex(F), S
0
) ← r(S
0
, S
1
) ∧ holds(F, S
1
)
EU(F
1
, F
2
) holds in state S
0
if there exists a maximal
path π: S
0
S
1
. . . such that for some S
n
occurring in π
we have that F
2
holds in S
n
and, for j = 0, . . . , n−1,
F
1
holds in S
j
:
holds(eu(F
1
, F
2
), S
0
) ← holds(F
2
, S
0
)
holds(eu(F
1
, F
2
), S
0
) ← holds(F
1
, S
0
) ∧ r(S
0
, S
1
) ∧
holds(eu(F
1
, F
2
), S
1
)
EG(F) holds in a state S
0
if there exists a maximal
path π starting from S
0
such that F holds in each state
of π. Since the set of states is finite, EG(F) holds
in S
0
if there exists a finite path S
0
. . . S
k
such that,
for i = 0, . . . , k, F holds in S
i
, and either (1) S
j
= S
k
,
for some 0 ≤ j < k, or (2) S
k
is a sink state. Thus,
the semantics of the operator EG is encoded by the
following rules:
holds(eg(F), S
0
) ← fpath(F, S
0
, S
0
)
holds(eg(F), S
0
) ←
holds(F, S
0
) ∧ r(S
0
, S
1
) ∧ holds(eg(F), S
1
)
holds(eg(F), S
0
) ← sink(S
0
) ∧ holds(F, S
0
)
where: (i) the predicate fpath(F, X, X) holds if there
exists a path from X to X itself, consisting of at least
one r arc, such that F holds in every state on the path:
fpath(F, X,Y ) ← holds(F, X) ∧ r(X,Y )
fpath(F, X, Z) ← holds(F, X) ∧ r(X,Y ) ∧
fpath(F,Y, Z)
and (ii) the predicate sink(X) holds if X has no suc-
cessor state:
sink(X) ← ¬succ(X )
succ(X) ← result(X, A,Y )
Finally, the following rule defines a property charac-
terizing the final state of a process, where the end
event associated with the process has been executed:
holds(final(P), Z) ← bp(P, S, E) ∧
holds(cf(E, end, P), Z)
The rules defining the semantics of the operator EG
are similar to the constraint logic programming defi-
nition proposed in (Nilsson and L
¨
ubcke, 2000). How-
ever, as already mentioned, in this paper we refer to
the notion of maximal path instead of infinite path.
Similarly to (Nilsson and L
¨
ubcke, 2000), our defi-
nition of the semantics of EG avoids the introduc-
tion of greatest fixed points of operators on sets of
states which are often required by the approach de-
scribed in (Clarke et al., 1999). Indeed, the rules
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
138

defining holds(eg(F), S
0
) are interpreted according to
the usual least fixpoint semantics (i.e., the least Her-
brand model (Lloyd, 1987)).
The encoding of the satisfaction relation for other
CTL operators, e.g, EF and AG, follows from the
equivalences defining them (Clarke et al., 1999). It is
worth noting that in some special cases the assump-
tion that paths are maximal, but not necessarily infi-
nite, matters. For instance, if S
0
is a sink state, then
holds(ag(F), S
0
) is true iff holds(F, S
0
) is true, since
the only maximal path starting from S
0
is the one con-
stituted by S
0
only. Finally, we would like to note
that the definition of the CTL semantics given here is
equivalent to the one in (Clarke et al., 1999) in the
presence of infinite computation paths only.
5 REASONING SERVICES
Our rule-based framework supports several reason-
ing services which can combine complex knowledge
about business processes from different perspectives,
such as the workflow structure, the ontological de-
scription, and the behavioral semantics. In this sec-
tion we will illustrate three such services: verification,
querying, and trace compliance checking.
Let us consider the following sets of rules: (1) B,
representing a set of BP schemas and the BP meta-
model defined in Section 2.1, (2) T , defining the be-
havioral semantics presented in Section 2.2, (3) O,
collecting the OWL triples and rules which repre-
sent the business reference ontology defined in Sec-
tion 3.1, (4) F , encoding the functional annotations
defined in Section 3.2, and (5) C TL, defining the se-
mantics of CTL presented in Section 4.
Let KB be the set of rules B ∪ T ∪ O ∪ F ∪
C TL. KB is called a Business Process Knowledge
Base (BPKB). We have that K B is a locally strat-
ified logic program and its semantics is unambigu-
ously defined by its unique perfect model, denoted by
Perf(K B) (Przymusinski, 1988).
5.1 Verification
Let us consider a BPKB KB. In the following we
present some examples of properties that can be spec-
ified and verified in our framework. A property is
specified by a predicate prop defined by a rule C in
terms of the predicates defined in KB. The verifi-
cation task is performed by checking whether or not
prop ∈ Perf(K B ∪ {C}).
(1) A very relevant behavioral property of a BP p is
that from any reachable state, it is possible to com-
plete the process, i.e., reach the final state. This prop-
erty, also known as option to complete (van der Aalst,
1998), can be specified by the following rule, stating
that the property opt com holds if the CTL property
AG(EF(final(p))) holds in the initial state of p:
opt com ← initial(X, p) ∧ holds(ag(ef (final(p))), X)
(2) Temporal queries allow us to verify the consis-
tency conditions for effects introduced in Section 3.2.
In particular, given a BPS p, inconsistencies due to
the violation of some integrity constraint defined in
the ontology by rules of the form false ← G (e.g.,
concept disjointness) can be verified by defining the
inconsistency property as follows:
inconsistency ← initial(X, p) ∧ holds(ef (false), X )
(3) Another relevant property of a BPS is executabil-
ity (Weber et al., 2010), according to which no activity
reached by the control flow should be unable to exe-
cute due to some unsatisfied enabling condition. In
our framework we can specify non-executability by
defining a predicate n exec which holds if it can be
reached a state where some activity A is waiting for
execution but is not possible to start its enactment.
n exec ← initial(X, p) ∧ holds(ef (and(cf(A1, A, p),
not(ex(en(A, p))))), X) ∧ activity(A)
(4) Temporal queries can also be used for the verifi-
cation of compliance rules, i.e., directives expressing
internal policies and regulations aimed at specifying
the way an enterprise operates. In our Handle Order
example, one such compliance rule may be that every
order is eventually closed. In order to verify whether
this property holds or not, we can define a noncom-
pliance property which holds if it is possible to reach
the final state of the process where, for some O, it
can be inferred that O is an order which is not closed.
In our example noncompliance is satisfied, and thus
the compliance rule is not enforced. In particular, if
the exception attached to the accept order task is trig-
gered, the enactment continues with the notify rejec-
tion task (due to the guards associated to g1), and the
order is never canceled nor fulfilled.
noncompliance ← initial(X, p) ∧
holds(ef (and(t
f
(O, rdf:type, bro:Order),and(
not(t
f
(O, rdf:type, bro:ClosedPO)), final(p))), X)
From an operational point of view, the verifica-
tion of a property prop is performed by evaluating
the query ← prop in KB ∪{C} using SLG-resolution,
that is, resolution for general logic programs aug-
mented with the tabling mechanism (Chen and War-
ren, 1996).
Theorem 1. Let C be a rule of the form prop ←
L
1
∧ . . . ∧ L
n
, where, for i = 1, . . . , n, the predicate
of L
i
is defined in K B and, whenever L
i
is of the
form holds( f , S), f is a term whose free variables
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
139

range over a finite domain. Then the evaluation of
the query ← prop in KB ∪ {C} terminates by using
SLG-resolution.
The above theorem can be proved by showing that
KB ∪ {C} satisfies the bounded-term-size property
(Chen and Warren, 1996).
5.2 Querying
The inference mechanism based on SLG-resolution
can be used for computing boolean answers to ground
queries, but also for computing, via unification,
substitutions for variables occurring in non-ground
queries. By exploiting this query answering mecha-
nism we can easily provide, besides the verification
service described in the previous section, also reason-
ing services for the retrieval of process fragments.
The following queries show how process frag-
ments can be retrieved according to different crite-
ria: q
1
computes every activity A (and the process
P where it occurs) which operates on an order as an
effect (e.g., create order and cancel order); q
2
com-
putes every exclusive branch G occurring along a path
delimited by two activities A and B which operate on
orders (e.g., create order) and invoices (e.g., fulfill or-
der), respectively; finally, q
3
is a refinement of q
2
,
where it is also required that the enactment of B is
always preceded by the enactment of A.
q
1
(A, P) ← eff(A, E
−
, E
+
, P) ∧
holds(t
f
(O, rdf:type, bro:Order),E
+
)
q
2
(A, G, B, P) ← eff(A, E
−
A
, E
+
A
, P) ∧ seq
+
(A, G, P) ∧
holds(t
f
(O, rdf:type, bro:Order),E
+
A
) ∧
exc branch(G) ∧ seq
+
(G, B, P) ∧ eff(B, E
−
B
, E
+
B
, P)
∧ holds(t
f
(I, rdf:type, bro:Invoice), E
+
B
)
q
3
(A, G, B, P) ← q
2
(A, G, B, P) ∧ initial(X, P) ∧
holds(not(eu(not(en(A, P)), en(B, P))), X)
5.3 Trace Compliance
The execution of a process is modeled as an exe-
cution trace (corresponding to a plan in the Fluent
Calculus), i.e., a sequence of actions of the form
[act(a
1
), . . . , act(a
n
)] where act is either begin or com-
plete. The predicate trace(S
1
, T, S
2
) defined below
holds if T is a sequence of actions that lead from state
S
1
to state S
2
:
trace(S
1
, [ ], S
2
) ← S
1
= S
2
trace(S
1
, [A|T], S
2
)←result(S
1
, A,U)∧trace(U, T, S
2
)
A correct trace T of a BPS P is a trace that leads
from the initial state to the final state of P, that is:
ctrace(T, P) ← initial(I, P) ∧ trace(I, T, Z) ∧
holds(final(P), Z)
Execution traces are commonly stored by BPM
systems as process logs, representing the evolution of
the BP instances that have been enacted. The correct-
ness of a trace t with respect to a given BPS p can be
verified by evaluating a query of the type
← ctrace(t, p)
where t is a ground list and p is a process name.
The rules defining the predicate ctrace can also be
used to generate the correct traces of a process p that
satisfy some given property. This task is performed
by evaluating a query of the type
← ctrace(T, p) ∧ cond(T )
where T is a free variable and cond(T) is a property
that T must enforce. For instance, we may want to
generate traces where the execution of a flow element
a is followed by the execution of a flow element b:
cond(T ) ← concat(T
1
, T
2
, T ) ∧ complete(a) ∈ T
1
∧
complete(b) ∈ T
2
The termination of querying and trace correctness
checking can be proved under assumptions similar to
the ones of Theorem 1. However, stronger assump-
tions are needed for the termination of trace genera-
tion in the case where we want to compute the set of
all correct traces satisfying a given condition, as this
set may be infinite in the presence of cycles.
6 RELATED WORK
Among several mathematical formalisms proposed
for defining a formal semantics of BP models, Petri
nets (van der Aalst, 1998) are the most used paradigm
to capture the execution semantics of the control flow
aspects of graph-based procedural languages. (The
BPMN case is discussed in (Dijkman et al., 2008).)
Petri net models enable a large number of analysis
techniques, but they do not provide a suitable basis to
represent and reason about additional domain knowl-
edge. In our framework we are able to capture the
token game semantics underlying workflow models,
and we can also declaratively represent constructs,
such as exception handling behavior or synchroniza-
tion of active branches only (inclusive merge), which,
due to their non-local semantics, are cumbersome to
capture in standard Petri nets. In addition, the logi-
cal grounding of our framework makes it easy to deal
with the modeling of domain knowledge and the inte-
gration of reasoning services.
Program analysis and verification techniques have
been largely applied to the analysis of process behav-
ior, e.g., (Fu et al., 2004; Liu et al., 2007). These
works are based on the analysis of finite state mod-
els through model checking techniques (Clarke et al.,
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
140

1999) where queries, formulated in some tempo-
ral logics, specify properties of process executions.
However, these approaches are restricted to proper-
ties regarding the control flow only (e.g., properties of
the ordering, presence, or absence of tasks in process
executions), and severe limitations arise when taking
into consideration ontology-related properties repre-
senting specific domain knowledge.
There is a growing body of contributions beyond
pure control flow verification. In (Weber et al., 2010)
the authors introduce the notion of Semantic Business
Process Validation, which aims at verifying proper-
ties related to the absence of logical errors which ex-
tend the notion of workflow soundness (van der Aalst,
1998). Validation is based on an execution semantics
where token passing control flow is combined with
the AI notion of state change induced by domain re-
lated logical preconditions/effects. The main result is
constituted by a validation algorithms which runs in
polynomial time under some restrictions on the work-
flow structure and on the expressivity of the logic un-
derlying the domain axiomatization, i.e., binary Horn
clauses. This approach is focused on providing effi-
cient techniques for the verification of specific prop-
erties, while the verification of arbitrary behavioral
properties, such as the CTL formulae allowed in our
framework, is not addressed. Moreover, our language
for annotations, encompassing OWL-RL, is more ex-
pressive than binary Horn clauses.
Several works propose the extension to business
process management of techniques developed in the
context of the semantic web
2
. Meta-model process
ontologies, e.g., (Francescomarino et al., 2009; Lin,
2008), are derived from BP modeling languages and
notations with the aim of specifying in a declarative,
formal, and explicit way concepts and constraints of
a particular language. Semantic Web Services ap-
proaches, such as OWL-S (Burstein et al., 2004) and
WSMO (Fensel et al., 2006), make an essential use
of ontologies in order to facilitate the automation of
discovering, combining and invoking electronic ser-
vices over the Web. To this end they describe ser-
vices from two perspectives: from a functional per-
spective a service is described in terms of its func-
tionality, preconditions and effects, input and output;
from a process perspective, the service behavior is
modeled as an orchestration of other services. How-
ever, in the above approaches the behavioral aspects
are abstracted away, since the semantics of the pro-
vided constructs is not axiomatized within their re-
spective languages, hampering the availability of rea-
soning services related to the execution of BPs.
To overcome such limitations, several solutions
2
See the SUPER EU Project (http://www.ip-super.org/).
for the representation of service compositions pro-
pose to translate the relevant aspects of the afore-
mentioned service ontologies into a more expressive
language, such as first-order logic, and to add a set
of axioms to this theory that constrains the models
of the theory to all and only the intended interpreta-
tions. Among them, (Sohrabi et al., 2009) adopts the
high-level agent programming language Golog (Re-
iter, 2001), (Battle et al., 2005; Narayanan and McIl-
raith, 2003) rely on Situation Calculus variants. How-
ever, such approaches are mainly tailored to auto-
matic service composition (i.e., finding a sequence
of service invocations such that a given goal is sat-
isfied). Thus, the support provided for process defini-
tion, in terms of workflow constructs, is very limited
and they lack a clear mapping from standard model-
ing notations. In contrast, our framework allows a
much richer procedural description of processes, di-
rectly corresponding to BPMN diagrams. Moreover,
a reference ontology can be used to “enrich” pro-
cess descriptions by means of annotations written in
OWL-RL, one of the most widespread languages for
ontology representation.
Other approaches based on Logic Programming
which are worth to mention are (Roman and Kifer,
2008; Montali et al., 2010). These approaches mainly
focus on the verification and on the enactment of BPs,
while we are not aware of specific extensions that deal
with the semantic annotation of procedural process
models with respect to domain ontologies.
Finally, with respect to our previous works (Smith
et al., 2012), we have proposed several extensions:
(1) we have increased the expressivity from a work-
flow perspective, by modeling arbitrary cycles, un-
structured diagrams and exceptions; (2) we have in-
troduced functional annotations and we have provided
a fluent-based semantics for their integration with the
control flow; finally, (3) we have introduced a general
verification mechanism based on CTL.
7 CONCLUSIONS
The rule-based approach for representing and reason-
ing about business processes presented in this paper
offers several advantages. First of all, it enables the
combination of the procedural and ontological per-
spectives in a very smooth and natural way, thus pro-
viding a uniform framework for reasoning on prop-
erties that depend on the sequence of operations that
occur during process enactment and also on the do-
main where the process operates. Another advantage
is the generality of the approach, which is open to fur-
ther extensions, since other knowledge representation
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
141

applications can easily be integrated, by providing a
suitable translation to logic programming rules. Our
approach does not introduce a new business process
modeling language, but provides a framework where
one can map and integrate knowledge represented by
means of existing formalisms. This is very important
from a pragmatic point of view, as one can express
process-related knowledge by using standard model-
ing languages such as BPMN for business processes
and OWL for ontologies, while adding extra reason-
ing services. Finally, since our rule-based represen-
tation can be directly mapped to a class of logic pro-
grams, we can use standard logic programming sys-
tems to perform reasoning tasks such as verification
and querying.
We have implemented in the XSB logic program-
ming system
3
the various sets of rules representing a
Business Process Knowledge Base, and on top of the
latter, the verification, querying, and trace compliance
services. The resolution mechanism based on tabling
(Chen and Warren, 1996) provided by XSB guaran-
tees a sound and complete evaluation of a large class
of queries (see Section 5.1). We have also integrated
the aforementioned services in the tool described in
(Smith et al., 2012), which implements an interface
between the BPMN and OWL representations of busi-
ness processes and reference ontology specifications
on one hand, and our rule-based representation on the
other hand, so that, as already mentioned, we can use
the reasoning facilities offered by our framework as
add ons to standard tools. First experiments are en-
couraging and show that very sophisticated reasoning
tasks can be performed on business process of small-
to-medium size in an acceptable amount of time and
memory resources. Currently, we are investigating
various program optimization techniques for improv-
ing the performance of our tool and enabling our ap-
proach to scale to large BP repositories.
REFERENCES
Battle, S., et al. (2005). Semantic Web Services Ontology.
http://www.w3.org/Submission/SWSF-SWSO.
Burstein, M., et al. (2004). OWL-S: Semantic Markup
for Web Services. W3C Member Submission, http://
www.w3.org/Submission/OWL-S/.
Chen, W. and Warren, D. S. (1996). Tabled Evaluation with
Delaying for General Logic Programs. JACM, 43:20–
74.
Clarke, E. M., Grumberg, O., and Peled, D. A. (1999).
Model Checking. The MIT Press.
3
The XSB Logic Programming System. Version 3.2:
http://xsb.sourceforge.net
Dijkman, R. M., Dumas, M., and Ouyang, C. (2008). Se-
mantics and Analysis of Business Process Models in
BPMN. Inf. Softw. Technol., 50:1281–1294.
Fensel, D., et al. (2006). Enabling Semantic Web Services:
The Web Service Modeling Ontology. Springer.
Francescomarino, C. D., Ghidini, C., Rospocher, M., Ser-
afini, L., and Tonella, P. (2009). Semantically-Aided
Business Process Modeling. In Int. Semantic Web
Conference, LNCS 5823, pages 114–129. Springer.
Fu, X., Bultan, T., and Su, J. (2004). Analysis of Interacting
BPEL Web Services. In Int. Conf. on World Wide Web,
pages 621–630. ACM Press.
Hepp, M., et al. (2005). Semantic Business Process Man-
agement: A Vision Towards Using Semantic Web Ser-
vices for Business Process Management. In Int. Conf.
on e-Business Engineering. IEEE Computer Society.
Hitzler, P., Kr
¨
otzsch, M., Parsia, B., Patel-Schneider,
P. F., and Rudolph, S. (2009). OWL 2 Web
Ontology Language. W3C Recommendation,
http://www.w3.org/TR/owl2-primer/.
Kindler, E. (2006). On the Semantics of EPCs: Resolving
the Vicious Circle. Data Knowl. Eng., 56(1):23–40.
Lin, Y. (2008). Semantic Annotation for Process Models:
Facilitating Process Knowledge Management via Se-
mantic Interoperability. PhD thesis, Norwegian Uni-
versity of Science and Technology.
Liu, Y., M
¨
uller, S., and Xu, K. (2007). A Static Compliance-
Checking Framework for Business Process Models.
IBM Syst. J., 46:335–361.
Lloyd, J. W. (1987). Foundations of logic programming.
Springer-Verlag New York, Inc.
Montali, M., Pesic, M., Aalst, W. M. P. v. d., Chesani, F.,
Mello, P., and Storari, S. (2010). Declarative Spec-
ification and Verification of Service Choreographies.
ACM Trans. Web, 4(1):3:1–3:62.
Narayanan, S. and McIlraith, S. (2003). Analysis and Simu-
lation of Web services. Comp. Networks, 42:675–693.
Nilsson, U. and L
¨
ubcke, J. (2000). Constraint Logic Pro-
gramming for Local and Symbolic Model-checking.
In Computational Logic, LNAI 1861. Springer.
OMG (2011). Business Process Model and Notation. http://
www.omg.org/spec/BPMN/2.0.
Przymusinski, T. C. (1988). On the Declarative Semantics
of Deductive Databases and Logic Programs. In Foun-
dations of Deductive Databases and Logic Program-
ming. Morgan Kaufmann Publishers Inc.
Reiter, R. (2001). Knowledge in Action: Logical Founda-
tions for Specifying and Implementing Dynamical Sys-
tems. The MIT Press.
Roman, D. and Kifer, M. (2008). Semantic Web Service
Choreography: Contracting and Enactment. In Int.
Semantic Web Conference, LNCS 5318, pages 550–
566. Springer.
Smith, F., Missikoff, M., and Proietti, M. (2012). Ontology-
Based Querying of Composite Services. In Business
System Management and Engineering, LNCS 7350,
pages 159–780. Springer.
Sohrabi, S., Prokoshyna, N., and McIlraith, S. A. (2009).
Web Service Composition via the Customization of
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
142

Golog Programs with User Preferences. In Concep-
tual Modeling: Foundations and Applications, pages
319–334. Springer.
ter Hofstede, A. M., van der Aalst, W. M. P., Adams, M.,
and Russell, N., editors (2010). Modern Business Pro-
cess Automation: YAWL and its Support Environment.
Springer.
Thielscher, M. (1998). Introduction to the Fluent Calculus.
Electron. Trans. Artif. Intell., 2:179–192.
van der Aalst, W. M. P. (1998). The Application of Petri
Nets to Workflow Management. J. Circuits, Systems,
and Computers, 8(1):21–66.
V
¨
olzer, H. (2010). A New Semantics for the Inclusive Con-
verging Gateway in Safe Processes. In Int. Conf. on
Business Process Management, LNCS 6336, pages
294–309, Berlin, Heidelberg. Springer.
Weber, I., Hoffmann, J., and Mendling, J. (2010). Beyond
Soundness: On the Verification of Semantic Business
Process Models. Distrib. Parallel Dat., 27:271–343.
Rule-basedBehavioralReasoningonSemanticBusinessProcesses
143
