
Evaluating Learning Algorithms for Stochastic Finite Automata
Comparative Empirical Analyses on Learning Models for Technical Systems
Asmir Voden
ˇ
carevi
´
c
1
, Alexander Maier
2
and Oliver Niggemann
2,3
1
International Graduate School Dynamic Intelligent Systems, University of Paderborn, Paderborn, Germany
2
inIT – Institute Industrial IT, OWL Universitiy of Applied Sciences, Lemgo, Germany
3
Fraunhofer IOSB – Competence Center Industrial Automation, Lemgo, Germany
Keywords:
Stochastic Finite Automata, Machine Learning, Technical Systems.
Abstract:
Finite automata are used to model a large variety of technical systems and form the basis of important tasks
such as model-based development, early simulations and model-based diagnosis. However, such models are
today still mostly derived manually, in an expensive and time-consuming manner.
Therefore in the past twenty years, several successful algorithms have been developed for learning various
types of finite automata. These algorithms use measurements of the technical systems to automatically derive
the underlying automata models.
However, today users face a serious problem when looking for such model learning algorithm: Which algo-
rithm to choose for which problem and which technical system? This papers closes this gap by comparative
empirical analyses of the most popular algorithms (i) using two real-world production facilities and (ii) using
artificial datasets to analyze the algorithms’ convergence and scalability. Finally, based on these results, several
observations for choosing an appropriate automaton learning algorithm for a specific problem are given.
1 INTRODUCTION
In computer science, the maturing of a field of re-
search happens normally in two phases: First, a num-
ber of algorithms are developed. Then in a second
phase, these algorithms are evaluated and compared.
Only after this second phase, their broad application
by non-experts becomes possible. For several rea-
sons, the second phase is often neglected, leaving
non-experts insecure and uneasy about the application
of newly developed algorithms.
The field of learning finite automata, where the
learning includes states and transitions, is an example
for this. Several algorithms have been developed (see
section 3 for an overview), but there is a lack of com-
parative studies. Different algorithms are often evalu-
ated in different application areas, using datasets that
are not always publicly available. Moreover, various
algorithms learn somewhat specific finite automata
for which the common comparison criteria have to be
established. This paper will help to close this gap by
introducing several important comparison criteria and
by evaluating algorithms on the same datasets.
In the rest of this section, a motivation for the
learning of automata is given. Section 2 then gives
an overview of stochastic finite automata formalisms.
Section 3 outlines the four algorithms ALERGIA,
MDI, BUTLA, and HyBUTLA for learning these au-
tomata. Criteria for comparing the algorithms are out-
lined in section 4. In section 5, comparative empiri-
cal analyses are conducted using two real-world pro-
duction facilities. Furthermore, due to the size and
structure limitations of the real datasets, we also use
artificial data in section 6 for further analyses on the
algorithms’ convergence and scalability. The results
are analyzed in section 7 and observations for the us-
age of these algorithms are given. Section 8 gives a
conclusion.
The learning of automata is a key technology
in a variety of fields such as model-based develop-
ment, verification, testing, and model-based diagno-
sis (Niggemann and Stroop, 2008). The importance
stems from the facts that (i) complex dynamical tech-
nical systems (such as production systems) can be
modeled using different types of finite automata and
(ii) a manual creation of these models is often too ex-
pensive and labor intensive.
A typical application scenario is the model-based
anomaly detection for technical systems: The more
complex technical system becomes, the more impor-
229
Voden
ˇ
carevi
´
c A., Maier A. and Niggemann O. (2013).
Evaluating Learning Algorithms for Stochastic Finite Automata - Comparative Empirical Analyses on Learning Models for Technical Systems.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 229-238
DOI: 10.5220/0004255702290238
Copyright
c
SciTePress

Offline learning
Online anomaly
detection
Sensor logs
Learning algorithm
Error
SYSTEM
MODEL
X
ANOMALY
DETECTION
DATA
Figure 1: Model-based anomaly detection.
tant are automatic and adaptive anomaly detection
and diagnosis systems. This increasing complexity
is mainly due to the high number of software-based
components and the usage of distributed architectures
in modern embedded systems. Ensuring proper func-
tioning of these technical systems has led to the de-
velopment of various monitoring, anomaly detection
and diagnosis techniques. Model-based approaches
have established themselves among the most success-
ful ones. However, they require a behavior model of
a system, which in most cases is still derived manu-
ally. Manual modeling of systems that exhibit state-
based, probabilistic, temporal, and/or continuous be-
havior is a hard task that requires a lot of efforts and
resources. Therefore, researchers have investigated
the possibilities to learn behavior models automati-
cally from logged data (see section 3).
The general approach to model-based anomaly de-
tection, which uses a learned behavior model, is il-
lustrated in figure 1. In the first phase, based on
logs of the system, a model of the normal behavior
is learned. Then, in the second phase, this normal
behavior model is used during a system’s operation
to detect anomalies. For this, the predictions of the
model are compared to the actual measurements from
the running system. If a significant discrepancy is de-
tected, the user is informed.
2 FINITE AUTOMATA
FORMALISMS
This paper deals with learning models for the three
types of technical systems: non-timed discrete event
systems, timed discrete event systems, and hybrid
systems. There are many mathematical formalisms
that can model their behavior, e.g. Bond graphs
(Narasimhan and Biswas, 2007), Petri nets (Cabasino
et al., 2010), continuous Petri nets (David and Alla,
1987), hybrid Petri nets (David and Alla, 2001), Par-
ticle filters (Wang and Dearden, 2009), Kalman fil-
ters (Hofbaur and Williams, 2002) and Bayesian net-
works (Zhao et al., 2005). Due to a number of positive
results for the learning of stochastic finite automata
from data, they are in the focus of this paper.
Non-timed Discrete Event Systems (nDES) show
a state-based behavior, i.e. they are represented by
a set of discrete states (modes of operation) and a fi-
nite set of events that trigger transitions between those
states (mode switches) (Cassandras and Lafortune,
2008). Such systems can be easily modeled as the
well-known Deterministic Finite Automaton (DFA)
as illustrated in figure 2(a): States are denoted by s
0
,
s
1
, s
2
, and s
3
, while letters a, b, and c denote events
that trigger transitions. The automaton is determin-
istic in a sense that one event can trigger only one
transition for each state.
b
a
s
0
s
1
s
2
c
s
3
(a) Deterministic finite automaton.
b, p(b)=0.2
a, p(a)=0.8
s
0
s
1
s
2
c, p(c)=0.7
s
3
p(s
0
)=0.2
p(s
1
)=0.1
(b) Stochastic deterministic finite automaton.
b, p(b)=0.2
a, p(a)=0.8
δ
2
=[3,6]
δ
1
=[1,4]
s
0
s
1
s
2
δ
3
=[7,14]
c, p(c)=0.7
s
3
p(s
0
)=0.2
p(s
1
)=0.1
(c) Stochastic deterministic timed automaton.
b, p(b)=0.2
θs
0
θs
3
θs
1
a, p(a)=0.8
δ
2
=[3,6]
δ
1
=[1,4]
s
0
s
1
s
2
θs
2
δ
3
=[7,14]
c, p(c)=0.7
s
3
p(s
0
)=0.2
p(s
1
)=0.1
(d) Stochastic deterministic hybrid automaton.
Figure 2: Deterministic finite automata for modeling tech-
nical systems.
Since the behavior of technical systems is always
subjected to statistical fluctuations (e.g. because of
noise or external disturbances), a model should take
this into account. Therefore, a stochastic version of
the DFA was developed (Carrasco and Oncina, 1994).
Stochastic Deterministic Finite Automaton
1
(SDFA)
1
Some authors denote such automata probabilistic,
rather than stochastic. E.g. see (Thollard et al., 2000). This
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
230

is illustrated in figure 2(b). In contrast to DFA, it mod-
els the probabilities of staying in a state or transiting
to another state given a specific event.
Technical systems also show a behavior over time,
i.e. timing information must be modeled also. These
systems are called timed Discrete Event Systems
(tDES). In such systems, it is very important at what
particular point in time an event happens. Clearly,
SDFA cannot be used to model tDES. For that reason,
Stochastic Deterministic Timed Automata (SDTA)
are used (stochastic version of timed automaton pre-
sented in (Alur and Dill, 1994)). An example is shown
in figure 2(c) and, unlike SDFAs, it contains time in-
tervals δ during which transitions must occur.
In addition to state-based, probabilistic and timed
behavior, real-world technical systems also exhibit
a mixture of (value-)discrete and (value-)continuous
behavior over time. So far, the presented formalisms
can only deal with discrete signals (i.e. events). But
within one discrete state, continuous signals often
change their values over time. An example is a flu-
idic system which has two states: First of all, values
such as pressure and flow change over time accord-
ing to one set of differential equations. But if a valve
is opened (the opening corresponds to an event), the
system moves to another state which is described by
a different set of differential equations.
Such systems, where discrete and continuous dy-
namics interact, are called hybrid systems (Alur et al.,
1995; Henzinger, 1996; Branicky, 2005). For model-
ing hybrid systems, the formalism of Stochastic De-
terministic Hybrid Automaton (SDHA) (a stochastic
version of hybrid automaton given in (Alur et al.,
1995)) can be used. A SDHA is illustrated in fig-
ure 2(d): The difference compared to SDTA are the θ
functions associated with discrete states. These func-
tions describe the change of continuous values over
time. A more detailed overview of finite automata
formalisms can be found in (Kumar et al., 2010).
3 LEARNING STOCHASTIC
FINITE AUTOMATA
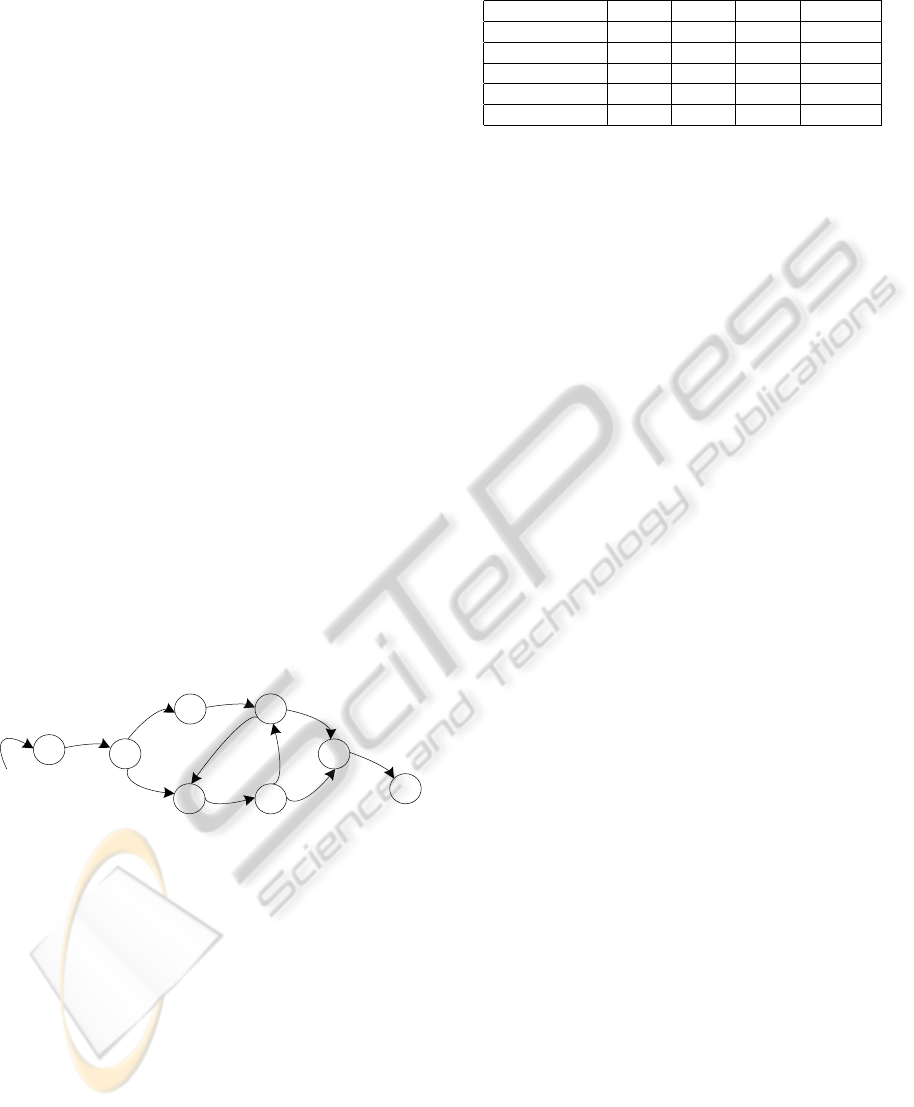
3.1 State Merging Approach
In this paper, four well-known automata learning al-
gorithms are presented and evaluated: ALERGIA,
MDI, BUTLA, and HyBUTLA. In general, all these
algorithms use the state merging approach for learn-
ing that is illustrated in figure 3.
also applies to other types of stochastic automata.
SYSTEM
LEARNED MODEL PREFIX TREE
STEP 1:
System Logs
STEP 2:
Prefix Detection
STEP 3:
State Merging
LOGGED
DATA
Figure 3: State merging approach for learning automata.
In step 1, all relevant signals are measured over
multiple production cycles of system’s normal oper-
ation. Measurements are logged in a database. For
timed systems, logs also include time stamps. For hy-
brid systems, both discrete and continuous signals are
recorded. The underlying data acquisition technolo-
gies are described e.g. in (Pethig et al., 2012).
An initial automaton called Prefix Tree Acceptor
(PTA) is then built in step 2. Each logged cycle of a
system represents one automaton learning example.
Each such example comprises multiple events of a
system which are defined as changes in discrete (typ-
ically binary) signals. These changes trigger transi-
tions between automaton states. A PTA is obtained
when common initial sequences of events of differ-
ent examples (i.e. example prefixes) are combined to-
gether. A PTA represents different examples as paths
from the initial state to one of the leaf states. Exam-
ples share the prefix parts of the paths. So a PTA is
just a smart way to store all examples.
In step 3, the learning takes place: compatible
pairs of PTA states are merged until the underlying
automata is identified. State merging makes the au-
tomaton smaller and more general. Different algo-
rithms use different compatibility tests.
3.2 Classification of Algorithms
In general, the learning algorithms can use learning
examples that can be both positive (coming from a
normal operation) and negative (coming from an ab-
normal operation) (Angluin, 1988). However, in real
technical systems the number of negative examples is
typically very small. Therefore, for the modeling of
technical systems (and in this paper) the focus is on
algorithms relying only on positive examples.
Automata learning algorithms can work either in
an online or an offline manner (Voden
ˇ
carevi
´
c et al.,
2011). Online algorithms can request additional ex-
EvaluatingLearningAlgorithmsforStochasticFiniteAutomata-ComparativeEmpiricalAnalysesonLearningModelsfor
TechnicalSystems
231

amples during the learning process. Offline algo-
rithms use only a given, static dataset, previously
logged in the system. All four given algorithms de-
scribed in this paper work in an offline manner.
The order of merging PTA states has a significant
influence on the learning performance, especially the
algorithm runtime (Niggemann et al., 2012). Learn-
ing algorithms normally use either a top-down or a
bottom-up merging order. In the top-down order,
states are checked for compatibility starting from the
initial state and progressing towards the leaf states.
When two states are found to be compatible using
some compatibility measure, their respective large
subtrees have to be recursively checked for compat-
ibility also. This is illustrated in figure 4 (left), where
subtrees t
1
and t
2
have to be compared, before the two
compatible states s
1
and s
2
are merged. In the bottom-
up approach (figure 4 (right)), such recursive checks
are minimized, as the merging process starts at leaf
states and moves towards the initial state. Algorithms
ALERGIA and MDI use the top-down, while BUTLA
and HyBUTLA use the bottom-up merging order.
t
1
t
2
s
1
s
2
t
s
1
s
2
Figure 4: Top-down (left) and bottom-up (right) merging
orders.
3.3 Learning Algorithms in a Nutshell
Stochastic deterministic finite automata (SDFAs) can
be learned automatically from data using the algo-
rithms ALERGIA and MDI. Stochastic determinis-
tic timed automata (SDTAs) are learned using the
BUTLA algorithm, while HyBUTLA learns stochas-
tic deterministic hybrid automata (SDHAs). Both
BUTLA and HyBUTLA learn corresponding au-
tomata classes with only one clock for tracking time.
In this section, these algorithms are briefly explained.
The ALERGIA Algorithm. After building a PTA
(see section 3.1), the ALERGIA (Carrasco and
Oncina, 1994) algorithm proceeds with checking the
compatibility of states in a top-down order. For every
single state, the probabilities of stopping in that state
or taking a specific transition to another state are com-
puted based on the number of its arriving, ending and
outgoing learning examples. Let the number of exam-
ples that arrive to state s
k
be g
k
, the number of exam-
ples that end in s
k
be f
k
(#), and the number of outgo-
ing examples with the event a be f
k
(a). The outgoing
probability for s
k
with the event a is then f
k
(a)/g
k
,
while the ending probability is f
k
(#)/g
k
. Once these
probabilities are computed, the compatibility between
any two states s
0
and s
1
is evaluated using the Hoeffd-
ing bound (Hoeffding, 1963):
f
0
g
0
−
f
1
g
1
>
s
1
2
log
2
α
1
√
g
o
+
1
√
g
1
. (1)
where (1 −α)
2
,α ∈ R,α > 0 is the probability that
the inequality is true. Here, f
0
and f
1
denote either
the number of outgoing or ending examples for the
states s
0
and s
1
respectively, as the Hoeffding bound
is computed for both probabilities. If the inequality
is true, the difference between estimated probabilities
(left side) is larger than a threshold which depends on
α (right side) and the states will not be merged. Oth-
erwise the states are declared as compatible, and then
their corresponding subtrees are also checked. This is
done by recursively evaluating Hoeffding bound for
all states in both subtrees. When states are finally
merged, the probabilities are recomputed for a new
state. In addition, due to the possible appearance of
non-determinism in a resulting automaton, it is made
deterministic by merging non-deterministic states and
transitions. Reported time complexity of ALERGIA
is O(n
3
), where n is the size of the input data. Formal
proof of convergence is given for ALERGIA’s version
called RLIPS in (Carrasco and Oncina, 1999).
The MDI Algorithm. In the ALERGIA algorithm,
the compatibility check based on Hoeffding bound
represents the local merging criterion, i.e. the proba-
bilities of two states and their subtrees are compared.
There is no global information that tells how different
is the whole newly obtained automaton from the pre-
vious one (before merging), or from the initial PTA.
Conversely, the algorithm Minimal Divergence Infer-
ence (MDI) takes this information into account. The
MDI algorithm (Thollard et al., 2000) trades off the
minimal divergence of the automaton from the learn-
ing examples and the minimal automaton size. The
states of the PTA A
0
are checked for compatibility in
the top-down order like in ALERGIA, but the merg-
ing criterion is based on the Kullback-Leibler (K-L)
divergence between two automata (that also represent
probability distributions of learning examples), rather
than on the Hoeffding bound. The K-L divergence
D(A||A
0
) between automata A and A
0
is calculated ac-
cording to:
D(A||A
0
) =
∑
x
i
p(x
i
|A)log
p(x
i
|A)
p(x
i
|A
0
)
, (2)
where x
i
represents one example used for learning.
Let A
1
be the temporary automaton obtained by suc-
cessfully merging states of the PTA A
0
. Further let
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
232
A
2
be a potential new automaton obtained by merg-
ing the states of A
1
. The divergence increment while
going from A
1
to A
2
is defined as:
∆(A
1
,A
2
) = D(A
0
||A
2
) −D(A
0
||A
1
). (3)
The merge of states of A
1
will be kept if the diver-
gence increment between obtained automaton A
2
and
A
1
is small enough relative to the size reduction. Let
α
M
denote the threshold, and |A
1
| and |A
2
| the sizes
of automata A
1
and A
2
, respectively (the number of
states). Then the compatibility criterion is:
∆(A
1
,A
2
)
|A
1
|−|A
2
|
< α
M
. (4)
If this inequality is true, the states are similar and will
stay permanently merged. Reported time complex-
ity of MDI is O(n
2
). Although some experiments in-
dicate that MDI significantly outperforms ALERGIA
(see e.g. (Vidal et al., 2005)), MDI lacks the proof of
convergence.
Please note that the MDI algorithm needs to do
the merge first in order to obtain the new automaton,
which is then compared with the previous one using
the criterion given by (4). In case the criterion is not
satisfied, the merge is discarded and the search for the
next potentially compatible state pair proceeds in the
previous automaton. The number of merges reported
in the results in the following sections represents only
those merges that were not discarded.
The BUTLA Algorithm. ALERGIA and MDI pro-
ceed top-down while searching for compatible states.
The BUTLA algorithm (Bottom-Up Timing Learning
Algorithm) firstly introduces the bottom-up strategy
(Maier et al., 2011). The criterion for the compatibil-
ity check uses the Hoeffding bound (see equation (1))
similar to the ALERGIA algorithm.
Additionally, BUTLA learns the timing of the
system. In a preprocessing step, for each avail-
able event a probability density function (PDF)—
probability over time—is calculated. If the PDF is the
sum of several Gaussian distributions, separate events
are created for each Gaussian distribution. In the pre-
fix tree creation and in the merging step, these events
are handled as different events.
The HyBUTLA Algorithm. The BUTLA algorithm
merging approach and the learning of timing informa-
tion is also applied in the HyBUTLA algorithm (Hy-
brid Bottom-Up Timing Learning Algorithm). Both
of them have the worst case runtime of O(n
3
) (sub-
quadratic in the average case). They differ only in
two aspects. First, HyBUTLA learns the behavior of
continuous output signals (based on continuous input
signals). For each state of the prefix tree, functions
that describe this behavior are approximated, e.g. us-
ing regression (Hastie et al., 2008). When two states
are merged, their portions of continuous data are com-
bined and functions for the newly created state are
learned. The HyBUTLA algorithm is the first hy-
brid automata learning algorithm (Voden
ˇ
carevi
´
c et al.,
2011). In the experiments presented in this paper, the
regression method used for learning continuous out-
put functions was multiple linear regression with lin-
ear terms.
The second difference between HyBUTLA and
BUTLA is that in BUTLA only the status of the
changing discrete signals defines a transition, while
the status of all other discrete signals is not preserved.
In HyBUTLA, the changing discrete signals also trig-
ger a transition, but the transition event includes the
status of all other discrete signals. This difference is
illustrated in figure 5. If the system has three discrete
signals: d
1
, d
2
, and d
3
, the change in d
2
(from 0 to
1) triggers the transition in both algorithms, but the
transition event for BUTLA is defined only as d
2
= 1,
while for HyBUTLA it contains also values of other
signals: {d
1
,d
2
,d
3
} = {0,1,0}
s
1
s
2
d
2
= 1
s
1
s
2
{d
1
,d
2
,d
3
} = {0,1,0}
Figure 5: Different event definitions for BUTLA (left) and
HyBUTLA (right).
4 CRITERIA FOR
ALGORITHM’S EVALUATION
Sections 5 and 6 evaluate the performance of the al-
gorithms using real-world and artificial data. In this
section, the used criteria and their importance for the
evaluation are outlined.
#states. The number of states is the primary measure
of the automaton size. In general, the goal is to ob-
tain the smallest possible model of a system, with the
highest possible accuracy.
#merges. The number of successful merges tells how
many pairs of states have been merged during learn-
ing. It is closely related to the number of states, as
the sum: (#states + #merges) equals to the number
of states in the prefix tree. State merging is used to
reduce the automaton size, but also to make it more
general. Intuitively, the more successful merges, the
higher is the generalization ability of the algorithm.
#comparisons. During a merging step, a search proce-
dure is performed in order to find as many compatible
states as possible. The more comparisons are made,
the higher is the chance that compatible states will be
found and merged.
EvaluatingLearningAlgorithmsforStochasticFiniteAutomata-ComparativeEmpiricalAnalysesonLearningModelsfor
TechnicalSystems
233

#determinizations. As stated earlier, some algorithms
use the top-down, while others use the bottom-up
merging order. While merging top-down the large
subtrees are encountered, thus the occurrence of non-
determinism in the automaton is more frequent. Num-
ber of determinizations indicates the portion of non-
determinism created during the merging step, that
needed to be resolved by the learning algorithm.
size reduction (%). Size reduction is the measure
of relative difference between the sizes of the final
automaton and the prefix tree. It is calculated as
#merges / (#states + #merges). Successful algorithms
can achieve high rates of size reduction.
R
2
(%): Averaged coefficient of determination
R
2
(%) over the automaton states shows the portion
of variability in the continuous data that is accounted
for by the regression function used for approximation.
Average R
2
can be measured only for the HyBUTLA
algorithm and it shows its ability to model the con-
tinuous dynamics of the system. In the following ex-
periments, multiple linear regression with linear terms
was used as the regression method.
5 EXPERIMENTS USING
REAL-WORLD SYSTEMS
5.1 The Lemgo Smart Factory
A first real-world case study was conducted using an
exemplary plant called the Lemgo Smart Factory at
the Institute Industrial IT in Lemgo, Germany. The
Lemgo Smart Factory is a hybrid technical system
that is used for storing, transporting, processing and
packing bulk materials (e.g. corn). It has a modular
design, uses both centralized and distributed automa-
tion concepts, and comprises around 250 measurable
signals.
Here, the corn processing unit was used as an ex-
ample. In total, logs from 15 production cycles are
available for learning the models. Logs contain the
time stamps, 9 discrete (binary) control signals, 9 con-
tinuous input signals, and machine’s active power as
the monitored continuous output variable.
The results are summarized in Table 1. It shows
the values for various comparison criteria outlined in
section 4. On this dataset, the algorithms had similar
performance in the sense of size reduction, number of
states and merges. It can be seen that BUTLA and Hy-
BUTLA performed significantly more comparisons
than ALERGIA and MDI. This is due to comparing
the timing of transitions, in addition to comparing
their probabilities. Even with simple method such as
multiple linear regression, high R
2
value is achieved.
Since ALERGIA and MDI use the top-down merging
order, they had to perform more determinizations.
Table 1: Algorithm comparison for Lemgo Smart Factory
data.
ALE MDI BUT HyBUT
#states 9 13 9 15
#merges 80 76 77 88
#comparisons 130 183 429 733
#determiniz. 44 171 21 14
reduction(%) 89.89 85.39 89.53 85.44
R
2
(%) - - - 94.54
5.2 The Jowat AG
The Jowat AG with headquarters in Detmold is one
of the leading suppliers of industrial adhesives. These
are mainly used in woodworking and furniture man-
ufacture, in the paper and packaging industry, the
textile industry, the graphic arts, and the automo-
tive industry. The company was founded in 1919
and has manufacturing sites in Germany in Detmold
and Zeitz, plus three other producing subsidiaries, the
Jowat Corporation in the USA, the Jowat Swiss AG,
and the Jowat Manufacturing in Malaysia. The sup-
plier of all adhesive groups is manufacturing approx.
70,000 tons of adhesives per year, with around 790
employees. A global sales structure with 16 Jowat
sales organizations plus partner companies is guaran-
teeing local service with close customer contact.
The data was logged in one of the plants, dur-
ing production of one product. In total 14 produc-
tion cycles were logged. The modeled part of the sys-
tem is the input raw material subsystem, which con-
tains 6 material supply units (smaller containers) con-
nected to a large container where materials are mixed.
Recorded discrete variables are 15 valve open signals
and their feedbacks (in total 30 discrete variables).
The continuous output variable whose dynamics was
learned is the large container weight. Continuous in-
put variables are weights of 6 smaller containers and
the pressure of the raw material pump. The results of
the algorithms’ comparison are given in Table 2.
Table 2: Algorithm comparison for Jowat AG data.
ALE MDI BUT HyBUT
#states 27 16 17 13
#merges 418 429 473 507
#comparisons 1025 605 4526 3576
#determiniz. 348 578 150 111
reduction(%) 93.93 96.4 96.5 97.5
R
2
(%) - - - 89.8
The trends are here similar as in Table 1. High
number of merges and high size reductions are ev-
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
234
ident for all algorithms. Again, BUTLA and Hy-
BUTLA do more comparisons, while ALERGIA and
MDI perform more determinizations. Also in this
moderately larger system, relatively high R
2
of around
90 % is achieved.
6 EXPERIMENTS USING
ARTIFICIAL DATA
In this section, learning examples were generated ar-
tificially from a given input model. This allows (i) for
the generation of arbitrarily complex examples and
(ii) for the assessment of the learned model by com-
paring it to the given input model.
6.1 Convergence Experiments
The experiments given here are conducted to exam-
ine how close the learning algorithms can converge
to the number of states in the predefined model that
generated the learning data. Algorithms use an artifi-
cial dataset randomly drawn according to a predefined
Reber-like model. It is illustrated in figure 6. Events
that trigger transitions are given together with their
corresponding transition probabilities. The original
Reber model (Reber, 1967) was changed in a way that
equal subsequent events do not occur (including tran-
sitions that have equal source and destination state),
because this cannot appear in production plants.
B(1.0)
T(0.5)
P(0.5)
X(1.0)
V(1.0)
Q(0.5)
S(0.5)
E(1.0)
W(0.5)
Y(0.5)
[7,20]
[1,3]
[1,3]
[4,8]
[4,7]
[2,9]
[10,15]
[8,9]
[6,9]
[7,15]
Figure 6: Reber-like automaton.
The number of generated learning examples was
1000. Example length was around 40 samples. In ad-
dition to discrete variables that trigger transitions (see
figure 6), one continuous output and five continuous
input signals were randomly generated according to
normal distribution for HyBUTLA experiments. In-
put and output signals have the mean value and stan-
dard deviation 220 ±22 and 1206 ±120.6, respec-
tively. Moreover, a randomly generated time interval
has been associated with every transition of the au-
tomaton. Summarized results for the four algorithms
are given in Table 3.
indent Due to the different way the HyBUTLA algo-
rithm defines the transition (see section 3.3), it gener-
ated significantly more states in the prefix tree, thus
Table 3: Algorithm comparison for artificial data.
ALE MDI BUT HyBUT
#states 13 5 11 8
#merges 14 22 16 3733
#comparisons 157 43 82 12081
#determiniz. 7 35 1 249
reduction(%) 51.85 81.48 59.26 99.79
having the high number of merges, comparisons, as
well as the high size reduction. However, it converged
to the automaton with the exact number of states of
the Reber-like automaton. ALERGIA had the worst
performance on this task, while MDI and BUTLA had
the same deviation from the target automaton.
6.2 HyBUTLA Scalability Experiments
The goal of scalability experiments is to evaluate the
HyBUTLA algorithm performance, in the presence of
the increasing number of two types of signals in the
system: discrete and continuous. A series of exper-
iments were conducted by increasing the number of
one type of signals, while keeping the number of the
other type constant. Results are given graphically for
created prefix tree acceptor (PTA) and learned hybrid
automaton. Given performance metrics include the
number of PTA states, the number of merges, average
model coefficient of determination (R
2
), size reduc-
tion (in relation to PTA size), and learning time.
In total, 22 artificial datasets were generated. Each
dataset comprises 10 learning examples. The size of
each learning example was picked from a range of
[150,250] samples with a random number generator
that uses an uniform distribution. Normal distribution
was used for generating independent continuous input
signals, as well as the output signal. The mean value
and standard deviation for input signals is 220 ±22,
and for the output it is 1206 ±120.6. Discrete sig-
nals were generated following an uniform distribu-
tion. They represent independent binary variables.
Locations and lengths of bit-switches are picked ran-
domly for every signal. Each discrete signal changes
two times per learning example. For easier reading,
the number of continuous signals will be denoted by
c, and the number of discrete signals by d.
6.2.1 Analysis with Constant Number of
Continuous Signals
In these experiments, d was increased from 1 to 50,
while c was kept constant at value 5. Figure 7(a)
shows the results for PTA. Its number of states in-
creases linearly with d. This makes the portions of
continuous data in each state smaller and easier to
approximate. Therefore, R
2
rises with d. The re-
EvaluatingLearningAlgorithmsforStochasticFiniteAutomata-ComparativeEmpiricalAnalysesonLearningModelsfor
TechnicalSystems
235

0 20 40 60
0
200
400
600
800
Number of discrete variables
Number of states
0 20 40 60
0
50
100
Number of discrete variables
Average R2 (%)
0 20 40 60
-1
-0.5
0
0.5
1
Number of discrete variables
Reduction (%)
0 20 40 60
0
2
4
6
8
Number of discrete variables
Learning time (s)
PTA plots for number of continuous variables = 5
#states
reduction(%)
runtime(s)
average R
2
(%)
#discrete signals d
#discrete signals d
#discrete signals d #discrete signals d
(a) PTA performance metrics for c = 5.
0 20 40 60
0
200
400
600
800
Number of discrete variables
Number of merges
0 20 40 60
0
10
20
30
40
Number of discrete variables
Average R2 (%)
0 20 40 60
80
85
90
95
100
Number of discrete variables
Reduction (%)
0 20 40 60
0
500
1000
1500
2000
Number of discrete variables
Learning time (s)
MERGE plots for number of continuous variables = 5
#merges
reduction(%)
runtime(s)
average R
2
(%)
#discrete signals d
#discrete signals d
#discrete signals d #discrete signals d
(b) Learned automaton performance metrics for c = 5.
Figure 7: Results for constant c.
duction is always zero for PTA experiments. PTA
construction time is approximately linear in d. Fig-
ure 7(b) shows results for merged PTAs (learned au-
tomata). The number of merges grows (approxi-
mately linearly) with d. As in the case of PTA, for
higher d, higher R
2
is obtained. In general, both size
reduction and learning time grow with d. The mea-
sured learning time is subquadratic. Since both PTA
size and the number of merges grow linearly with d
(i.e. with the size of dominantly discrete system), the
size of the final learned model will also grow. Ex-
periments are done for more values of constant c, and
the results are similar (not shown due to space restric-
tions).
6.2.2 Analysis with Constant Number of
Discrete Signals
Here c was increased from 1 to 50, while d was kept at
value 5. Figure 8(a) gives the results for PTA. Since
states are derived based on changes in discrete sig-
0 20 40 60
88
88.5
89
89.5
90
Number of continuous variables
Number of states
0 20 40 60
20
40
60
80
100
Number of continuous variables
Average R2 (%)
0 20 40 60
-1
-0.5
0
0.5
1
Number of continuous variables
Reduction (%)
0 20 40 60
0
1
2
3
4
Number of continuous variables
Learning time (s)
PTA plots for number of discrete variables = 5
#states
reduction(%)
runtime(s)
average R
2
(%)
#continuous signals c
#continuous signals c
#continuous signals c #continuous signals c
(a) PTA performance metrics for d = 5.
0 20 40 60
80
80.5
81
81.5
82
Number of continuous variables
Number of merges
0 20 40 60
0
10
20
30
40
Number of continuous variables
Average R2 (%)
0 20 40 60
90
91
92
93
Number of continuous variables
Reduction (%)
0 20 40 60
5
10
15
Number of continuous variables
Learning time (s)
MERGE plots for number of discrete variables = 5
#merges
reduction(%)
runtime(s)
average R
2
(%)
#continuous signals c
#continuous signals c
#continuous signals c #continuous signals c
(b) Learned automaton performance metrics for d = 5.
Figure 8: Results for constant d.
nals only, the increase in c does not generate the new
ones. However, the growth of c increases the aver-
age R
2
. Like before, reduction is zero, while learning
time grows with c. Results for the learned automata
are shown in figure 8(b). Merging criteria do not in-
clude continuous signals, thus the number of merges
is constant in c (and so is the reduction). Both R
2
and learning time grow approximately linearly with c.
Since the model size remains unchanged, one should
always try to log and use as many input signals as
possible since more predictors approximate the out-
put signal better. More experiments were conducted
for different values of constant d and similar trends
are observed (not shown due to space restrictions).
7 DISCUSSION
Based on the analysis presented in this paper, several
general observations for learning behavior models for
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
236

technical systems are given. These observations could
be used in practice by non-experts. Table 4 gives the
overview of stochastic automata formalisms suitable
for modeling the three types of technical systems:
non-timed Discrete Event System (nDES), timed Dis-
crete Event System (tDES), and a Hybrid System
(HS). Table also gives the algorithms that can success-
fully learn such automata.
Table 4: Systems, models and learning algorithms.
System nDES tDES HS
Model SDFA SDTA SDHA
Algorithm
ALERGIA
BUTLA HyBUTLA
MDI
Analyses in real-world systems have shown sim-
ilar trends for smaller exemplary Lemgo Smart Fac-
tory and moderately bigger Jowat AG datasets. It can
be observed that all four algorithms achieved similar
and relatively high size reduction rates in both cases,
which demonstrates their ability to produce small and
more general models. Obtained models that have 9–
27 states can be easily visualized, understood and in-
terpreted by humans, thus they provide a good insight
in the system’s modes of operation and its behavior
in general. Getting such insight by using the pre-
fix trees with hundreds of states would not be possi-
ble. It should be noted that the HyBUTLA algorithm
was able to create models with average R
2
of around
90% for both systems using relatively simple regres-
sion method such as multiple linear regression. These
models represent the continuous dynamics of the sys-
tems quite well. Furthermore, it can be seen that the
bottom-up algorithms (BUTLA and HyBUTLA) per-
form more thorough search for compatible states, as
they make more comparisons of the states. Intuitively,
this advantage is payed with their increased runtime.
Top-down algorithms create more non-determinism
in the model that they need to resolve.
The convergence experiments on artificial data
given in section 6.1 have demonstrated that the algo-
rithms can converge either to the exact or close to the
number of states of the predefined model that gen-
erated the learning data. Since most real-world pro-
duction systems are hybrid systems, a special atten-
tion was devoted to the HyBUTLA algorithm in sec-
tion 6.2. Based on the conducted experiments with
changing number of discrete (d), and continuous (c)
signals, further observations are derived and summa-
rized in table 5. For dominantly discrete systems, one
can expect to obtain large PTAs, but at the same time
to benefit from merging in the sense of size reduc-
tion. Very small models (high reduction rates) could
be obtained. Unfortunately, this typically produces
lower accuracy of approximating continuous output
signals (low average R
2
). For dominantly continuous
systems, the situation is converse. With smaller d,
PTAs of the small size are obtained. Larger c does
not influence neither the PTA size, nor the number of
merges. Small d enables very few or no merges, thus
merging does not bring significant benefit in modeling
such systems in the sense of size reduction. However,
typically higher average R
2
values can be obtained.
Table 5: Observations for modeling hybrid systems with
HyBUTLA algorithm.
Dominantly discrete Dominantly continuous
system system
(larger d, smaller c) (smaller d, larger c)
larger PTA smaller PTA
many merges fewer or no merges
higher size reduction lower size reduction
lower average R
2
higher average R
2
8 CONCLUSIONS
In order to tackle the drawbacks of manual model-
ing of technical systems, several algorithms can be
used for learning behavior models automatically from
logged data. This paper focused on four such algo-
rithms which learn models using the formalism of
stochastic finite automata. Automata can represent
non-timed and timed discrete event systems, as well
as the hybrid systems. The usability of the algorithms
ALERGIA, MDI, BUTLA and HyBUTLA has been
evaluated and compared in real-world as well as in an
artificial data settings. In general, all four algorithms
have produced small and tractable models, which pro-
vide an easy and good insight in the underlying be-
havior of the corresponding technical systems. The
paper also gives several general observations for ap-
plying such algorithms to various types of technical
systems.
This paper provided a comparative empirical anal-
yses of the aforementioned algorithms. The future
work will mainly include theoretical comparisons.
REFERENCES
Alur, R., Courcoubetis, C., Halbwachs, N., Henzinger,
T. A., h. Ho, P., Nicollin, X., Olivero, A., Sifakis, J.,
and Yovine, S. (1995). The algorithmic analysis of hy-
brid systems. Theoretical Computer Science, 138:3–
34.
Alur, R. and Dill, D. (1994). A theory of timed automata.
Theoretical Computer Science, vol. 126:183–235.
Angluin, D. (1988). Identifying languages from stochas-
tic examples. In Yale University technical report,
YALEU/DCS/RR-614.
EvaluatingLearningAlgorithmsforStochasticFiniteAutomata-ComparativeEmpiricalAnalysesonLearningModelsfor
TechnicalSystems
237

Branicky, M. S. (2005). Introduction to hybrid systems. In
Handbook of Networked and Embedded Control Sys-
tems, pages 91–116.
Cabasino, M. P., Giua, A., and Seatzu, C. (2010). Fault de-
tection for discrete event systems using petri nets with
unobservable transitions. Automatica, 46(9):1531–
1539.
Carrasco, R. C. and Oncina, J. (1994). Learning stochas-
tic regular grammars by means of a state merging
method. In GRAMMATICAL INFERENCE AND AP-
PLICATIONS, pages 139–152. Springer-Verlag.
Carrasco, R. C. and Oncina, J. (1999). Learning determinis-
tic regular grammars from stochastic samples in poly-
nomial time. In RAIRO (Theoretical Informatics and
Applications), volume 33, pages 1–20.
Cassandras, C. G. and Lafortune, S. (2008). Introduction to
Discrete Event Systems. 2.ed. Springer.
David, R. and Alla, H. (1987). Continuous petri nets. In
Proc. of the 8th European Workshop on Application
and Theory of Petri Nets, pages 275–294. Zaragoza,
Spain.
David, R. and Alla, H. (2001). On hybrid petri nets. Dis-
crete Event Dynamic Systems, 11(1-2):9–40.
Hastie, T., Tibshirani, R., and Friedman, J. (2008). The el-
ements of statistical learning: data mining, inference
and prediction. Springer, 2 edition.
Henzinger, T. A. (1996). The theory of hybrid automata.
In Proceedings of the 11th Annual IEEE Symposium
on Logic in Computer Science, LICS ’96, pages 278–
292, Washington, DC, USA. IEEE Computer Society.
Hoeffding, W. (1963). Probability inequalities for sums of
bounded random variables. Journal of the American
Statistical Association, 58(301):pp. 13–30.
Hofbaur, M. W. and Williams, B. C. (2002). Mode esti-
mation of probabilistic hybrid systems. In Intl. Conf.
on Hybrid Systems: Computation and Control, pages
253–266. Springer Verlag.
Kumar, B., Niggemann, O., and Jasperneite, J. (2010). Sta-
tistical models of network traffic. In International
Conference on Computer, Electrical and Systems Sci-
ence. Cape Town, South Africa.
Maier, A., Voden
ˇ
carevi
´
c, A., Niggemann, O., Just, R., and
J
¨
ager, M. (2011). Anomaly detection in production
plants using timed automata. In 8th International
Conference on Informatics in Control, Automation
and Robotics (ICINCO), pages 363–369. Noordwijk-
erhout, The Netherlands.
Narasimhan, S. and Biswas, G. (2007). Model-based diag-
nosis of hybrid systems. Systems, Man and Cybernet-
ics, Part A: Systems and Humans, IEEE Transactions
on, 37(3):348 –361.
Niggemann, O., Stein, B., Voden
ˇ
carevi
´
c, A., Maier, A., and
Kleine B
¨
uning, H. (2012). Learning behavior mod-
els for hybrid timed systems. In Twenty-Sixth Confer-
ence on Artificial Intelligence (AAAI-12), pages 1083–
1090, Toronto, Ontario, Canada.
Niggemann, O. and Stroop, J. (2008). Models for model’s
sake: why explicit system models are also an end
to themselves. In ICSE ’08: Proceedings of the
30th international conference on Software engineer-
ing, pages 561–570, New York, NY, USA. ACM.
Pethig, F., Kroll, B., Niggemann, O., Maier, A., Tack, T.,
and Maag, M. (2012). A generic synchronized data
acquisition solution for distributed automation sys-
tems. In Proc. of the 17th IEEE International Conf.
on Emerging Technologies and Factory Automation
ETFA’2012, Krakow, Poland (in press).
Reber, A. S. (1967). Implicit learning of artificial gram-
mars. Journal of Verbal Learning and Verbal Behav-
ior, 6(6):855 – 863.
Thollard, F., Dupont, P., and de la Higuera, C. (2000). Prob-
abilistic DFA inference using Kullback-Leibler diver-
gence and minimality. In Proc. of the 17th Interna-
tional Conf. on Machine Learning, pages 975–982.
Morgan Kaufmann.
Vidal, E., Thollard, F., de la Higuera, C., Casacuberta, F.,
and Carrasco, R. C. (2005). Probabilistic finite-state
machines-part ii. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 27:1026–1039.
Voden
ˇ
carevi
´
c, A., Kleine B
¨
uning, H., Niggemann, O., and
Maier, A. (2011). Identifying behavior models for
process plants. In Proc. of the 16th IEEE International
Conf. on Emerging Technologies and Factory Automa-
tion ETFA’2011, pages 937–944, Toulouse, France.
Wang, M. and Dearden, R. (2009). Detecting and Learning
Unknown Fault States in Hybrid Diagnosis. In Pro-
ceedings of the 20th International Workshop on Prin-
ciples of Diagnosis, DX09, pages 19–26, Stockholm,
Sweden.
Zhao, F., Koutsoukos, X. D., Haussecker, H. W., Reich, J.,
and Cheung, P. (2005). Monitoring and fault diagno-
sis of hybrid systems. IEEE Transactions on Systems,
Man, and Cybernetics, Part B, 35(6):1225–1240.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
238
