An Adaptive Incremental Clustering Method based on the Growing

Neural Gas Algorithm

Mohamed-Raﬁk Bouguelia, Yolande Bela

ıd and Abdel Bela

ıd

Universit

e de Lorraine, LORIA, UMR 7503, Vandoeuvre-les-Nancy F-54506, France

Keywords:

Incremental Clustering, Online Learning, Unsupervised Neural Clustering, Data Streams.

Abstract:

Usually, incremental algorithms for data streams clustering not only suffer from sensitive initialization pa-

rameters, but also incorrectly represent large classes by many cluster representatives, which leads to decrease

the computational efﬁciency over time. We propose in this paper an incremental clustering algorithm based

on ”growing neural gas” (GNG), which addresses this issue by using a parameter-free adaptive threshold to

produce representatives and a distance-based probabilistic criterion to eventually condense them. Experiments

show that the proposed algorithm is competitive with existing algorithms of the same family, while maintaining

fewer representatives and being independent of sensitive parameters.

1 INTRODUCTION

Recently, research focused on designing efﬁcient al-

gorithms for clustering continuous data streams in

an incremental way, where each data can be visited

only once and processed dynamically as soon as it is

available. Particularly, unsupervised incremental neu-

ral clustering methods take into account relations of

neighbourhood between representatives, and show a

good clustering performance. Among these methods,

GNG algorithm (Fritzke, 1995) has attracted consid-

erable attention. It allows dynamic creation and re-

moval of neurons (representatives) and edges between

them during learning by maintaining a graph topol-

ogy using a competitive Hebbian Learning strategy

(Martinetz, 1993). Each edge has an associated age

which is used in order to remove old edges and keeps

the topology dynamically updated. After adapting the

graph topology using a ﬁxed number of data-points

from the input space (i.e. a time period), a new neu-

ron is inserted between the two neighbouring neurons

that cumulated the most important error. Unlike usual

clustering methods (e.g. Kmeans), it does not require

initial conditions such as a predeﬁned number of clus-

ters and their initialization. This represents an impor-

tant feature in the context of data stream clustering

where we have no prior knowledge about the whole

dataset. However, in GNG, the creation of a new neu-

ron is made periodically, and a major disadvantage

concerns the choice of this period. For this purpose,

some adaptations that relaxes this periodical evolu-

tion have been proposed. The main incremental vari-

ants are IGNG (Prudent and Ennaji, 2005), I2GNG

(Hamza et al., 2008) and SOINN (Shen et al., 2007).

Unfortunately, the fact that these methods depend on

some sensitive parameters that must be speciﬁed prior

to the learning, reduces the importance of their incre-

mental nature. Moreover, large classes are unneces-

sarily modelled by many neurons representing many

small cluster fragments, leading to a signiﬁcant drop

of computational efﬁciency over time.

In this paper we propose a GNG based incremen-

tal clustering algorithm (AING) where the decision

of producing a new neuron from a new coming data-

point is based on an adaptive parameter-free distance

threshold. The algorithm overcomes the shortcoming

of excessive number of neurons by condensing them

based on a probabilistic criterion, and building a new

topology with a fewer number of neurons, thus pre-

serving time and memory resources. The algorithm

depends only on a parameter generated by the system

requirements (e.g. allowed memory budget), and un-

like the other algorithms, no parameter related to a

speciﬁc characteristics dataset needs to be speciﬁed.

Indeed, it can be really difﬁcult for a user to esti-

mate all the parameters that are required by a learn-

ing algorithm. According to (Keogh et al., 2004),

”A parameter-free algorithm would limit our ability

to impose our prejudices, expectations, and presump-

tions on the problem at hand, and would let the data

itself speak to us”. An algorithm which uses as few

parameters as possible without requiring prior knowl-

Bouguelia M., Belaïd Y. and Belaïd A. (2013).

An Adaptive Incremental Clustering Method based on the Growing Neural Gas Algorithm.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 42-49

DOI: 10.5220/0004256600420049

 SciTePress

edge is strongly preferred, especially when the whole

dataset is not available beforehand (i.e. a data-stream

conﬁguration).

This paper is organized as follows. In section

2, we describe a brief review of some incremental

clustering methods (including the GNG based ones),

and analyse their problems. Then the algorithm we

propose is presented in section 3. In section 4, we

present our experimental evaluation on synthetic and

real datasets. In section 5, we give the conclusion and

we present some perspectives of this work.

2 RELATED WORK

Before describing some incremental methods and

discussing their related problems, we ﬁrstly give

some notations to be used in the rest of this paper:

x refers to a data-point, y to a neuron (cluster repre-

sentative), X

is the set of data-points that are already

assigned to neuron y, V

is the set of current neurons

that are neighbours of y (neurons linked to y by an

edge), w

is the reference vector of neuron y, and n

= |X

| is the number of data-points currently assigned

to y.

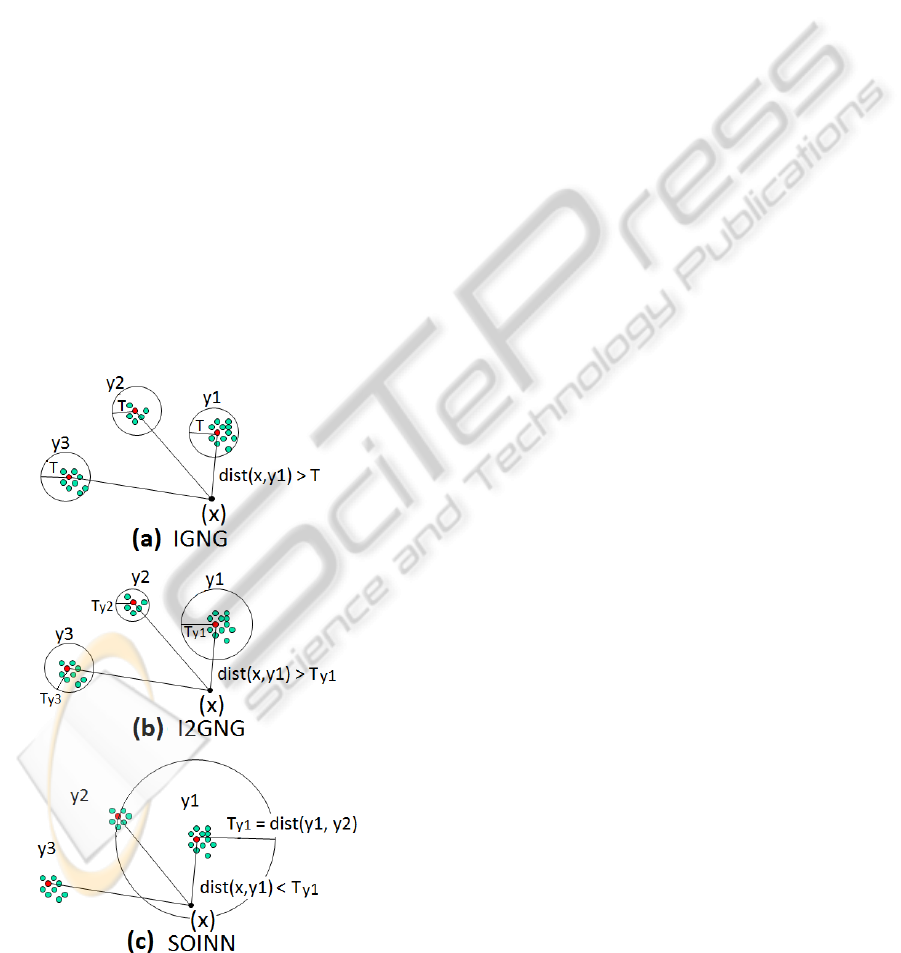
Figure 1: Threshold based methods.

The basic idea of the Incremental Growing Neural

Gas algorithm (IGNG) (Prudent and Ennaji, 2005) is

that the decision of whether a new coming data-point

x is close enough to its nearest neurons is made ac-

cording to a ﬁxed distance threshold value T (Figure

1(a)). Nevertheless, the main drawback of this ap-

proach is that the threshold T is globally the same for

all neurons and must be provided as a parameter prior

to the learning. There is no way to know beforehand

which value is convenient for T , especially in a con-

ﬁguration where the whole dataset is not available.

I2GNG (Hamza et al., 2008) is an improved ver-

sion of IGNG where each neuron y has its own lo-

cal threshold value (Figure 1(b)) which is continu-

ously adapted during learning. If there is currently

no data-point assigned to a neuron y, then its associ-

ated threshold is a default value T which is an input

parameter given manually as in IGNG; otherwise, the

threshold is deﬁned as

d + ασ, where

d is the mean

distance of y to its currently assigned data-points, σ is

the corresponding standard deviation, and α a param-

eter. Choosing ”good” values for parameters T and α

is important since the evolution of the threshold will

strongly depends on them. This clearly makes sys-

tems using such an algorithm dependent on an expert

user and gives less emphasis to its incremental nature.

In the Self-Organizing Incremental Neural Net-

work (SOINN) (Shen et al., 2007), the threshold of a

given neuron y is deﬁned as the maximum distance of

neuron y to its current neighbours if they exist, other-

wise it is the distance of y to its nearest neuron among

the existing ones (Figure 1(c)). SOINN’s threshold

is often more sensitive to the creation order of neu-

rons (induced by the arrival order of data-points), es-

pecially in ﬁrst steps. Furthermore, SOINN deletes

isolated neurons and neurons having only one neigh-

bour when the number of input data-points is a multi-

ple of a parameter λ (a period).

Many other parameter-driven methods have been

designed especially for data stream clustering, among

this methods we can cite: Stream (O’Callaghan

et al., 2002), CluStream (Aggarwal et al., 2003) and

Density-Based clustering for data stream (Chen and

Tu, 2007).

There are several variants of Kmeans that are said

”incremental”. The one proposed in (Shindler et al.,

2011) is based on a cost of creation of cluster centers;

the higher it is, the fewer is the number of created

clusters. The cost is eventually incremented and the

cluster centers are re-evaluated. However, the algo-

rithm assumes that the size of the processed dataset is

known and ﬁnite.

AnAdaptiveIncrementalClusteringMethodbasedontheGrowingNeuralGasAlgorithm

3 PROPOSED ALGORITHM

(AING)

In this section, we propose a scalable incremen-

tal clustering algorithm that is independent of sen-

sitive parameters, and dynamically creates neurons

and edges between them as data come. It is called

”AING” for Adaptive Incremental Neural Gas.

3.1 General Behaviour

The general schema of AING can be expressed ac-

cording to the following 3 cases. Let y

and y

re-

spectively be the nearest and the second nearest neu-

rons from a new data-point x, such that dist(y

,x) <

dist(y

,x).

1. if x is far enough from y

: a new neuron y

new

created at x (Figure 2, 1

case).

2. if x is close enough to y

but far enough from y

a new neuron y

new

is created at x, and linked to y

by a new edge (Figure 2, 2

case).

3. if x is close enough to y

and close enough to y

(Figure 2, 3

case):

• move y

and its neighbouring neurons towards

x, i.e. modify their reference vectors to be less

distant from x.

• increase the age of y

’s edges

• link y

to y

by a new edge (reset its age to 0 if

it already exists)

• activate the neighbouring neurons of y

• delete the old edges if any

An age in this context is simply a value associ-

ated to each existing edge. Each time a data-point x is

assigned to the winning neuron y

(the 3

case), the

age of edges emanating from this neuron is increased.

Each time a data-point x is close enough to neurons y

and y

, the age of the edge linking this two neurons is

reset to 0. If the age of an edge continues to increase

without being reset, it will reaches a maximum age

value and the edge will be considered ”old” and thus

removed.

A data-point x is considered far (respectively

close) enough from a neuron y, if the distance be-

tween x and y is higher (respectively smaller) than a

threshold T

. The following subsection shows how

this threshold is deﬁned.

3.2 AING Distance Threshold

Since the input data distribution is unknown, we de-

ﬁne a parameter-free adaptive threshold T

which is

Figure 2: AING general cases.

local to each neuron. The idea is to make the thresh-

old T

of a neuron y, dependent on the distances to

data in its neighbourhood. The neighbourhood of y

consists of data-points previously assigned to y (for

which y is the nearest neuron), and data-points as-

signed to the neighbouring neurons of y (neurons that

are linked to y by an edge).

According to formula 1, the threshold T

of a neu-

ron y is deﬁned as the sum of distances from y to its

data-points, plus the sum of weighted distances from

y to its neighbouring neurons

, averaged on the total

number of the considered distances. In the case where

the neuron y has no data-points that were already as-

signed to it (X

is empty) and has no neighbour (V

empty), then we consider the threshold T

as the half

distance from y to its nearest neuron.











∑

e∈X

dist(y,e)+

∑

e∈V

|×dist(y,e)

∑

e∈V

if X

0 ∨V

dist(y, ˜y)

, ˜y = argmin

˜y6=y

dist(y, ˜y) otherwise

(1)

Figure 3: AING threshold deﬁnition.

Note that we do not need to save data-points that

are already seen in order to compute this threshold.

The distance is weighted by the number of data-points

associated to the neighbouring neuron

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

It is incrementally computed each time a new data-

point comes, by updating some information associ-

ated to each neuron (e.g. number of data-points as-

sociated to a neuron, the sum of their distances to

this neuron, etc.). If we consider the example of Fig-

ure 3, there are 3 data-points assigned to y

(namely

, x

and x

), and two neurons that are neighbours

of y

(namely y

with 4 assigned data-points, and

with 5 data-points). In this case, the threshold

associated to the neuron y

is computed as T

dist(y

)+dist(y

)+4dist(y

)+5dist(y

)

3+4+5

As we can see, the proposed threshold is indepen-

dent of parameters and evolves dynamically accord-

ing to the data and the topology of neurons.

3.3 AING Merging Process

Since data is processed online, it is usually common

that algorithms for data stream clustering generate

many cluster representatives. However, this may sig-

niﬁcantly compromise the computational efﬁciency

over time. Instead of introducing parameters in the

threshold computation to control the number of cre-

ated neurons, AING can eventually reduce the num-

ber of neurons through the merging process. Indeed,

when the number of current neurons reaches an up-

per bound (up bound), some close neurons can be

merged.

The merging process globally follows the same

scheme as previously, but instead of relying on a hard

rule based on a threshold, it uses a more relaxed rule

based on a probabilistic criterion. Saying that ”a neu-

ron y is far enough from its nearest neuron ˜y” is ex-

pressed as the probability that y will not be assigned

to ˜y, according to the formula P

y, ˜y

|×dist(y, ˜y)

. This

probability is proportional to the distance between the

two neurons (dist(y, ˜y)) and to the number of data-

points assigned to y (|X

|), that is, the more y is large

and far from ˜y, the more likely it is to remain not

merged. The probability is in contrast inversely pro-

portional to a variable κ, which means that by incre-

menting κ, any given neuron y will have more chance

to be merged with its nearest neuron. Let

d be the

mean distance of all existing neurons to the center-of-

mass of the observed data-points. κ is incremented by

κ = κ +

d each time the neurons need to be more con-

densed, i.e. until the merging process takes effect and

the number of neurons becomes less than the speciﬁed

limit up bound. Note that P

y, ˜y

as speciﬁed may be

higher than 1 when κ is not yet sufﬁciently big; a bet-

ter formulation would be P

y, ˜y

= min(

|×dist(y, ˜y)

,1),

to guarantee it to be always a true probability.

The merging process is optional. Indeed,

up bound can be set to +∞ if desired. Alterna-

tively, the merging process can be triggered at any

time chosen by the user, or by choosing the parame-

ter up bound according to some system requirements

such as the memory budget that we want to allocate

for the clustering task, or the maximum latency time

tolerated by the system due to a high number of neu-

rons.

Finally, the code is explicitly presented in Algo-

rithms 1 and 2, which provide an overall insight on

the AING’s method of operation. They both follow

the same scheme described in section 3.1. Algorithm

1 starts from scratch and incrementally processes each

data-point from the stream using the adaptive distance

threshold described in section 3.2. When the num-

ber of current neurons reaches a limit, Algorithm 2 is

called and some neurons are grouped together using

the probabilistic criterion described in section 3.3. We

just need to point out two additional details appearing

in our algorithms:

• If a data-point x is close enough to its two near-

est neurons y

and y

, it is assigned to y

and

the reference vector of this later and its neigh-

bours are updated (i.e. they move towards x) by

a learning rate: ε

for y

and ε

for its neighbours

(lines 15-17 of Algorithm 1). Generally, a too big

learning rate implies instability of neurons, while

a too small learning rate implies that neurons do

not learn enough from their assigned data. Typ-

ical values are 0 < ε

 1 and 0 < ε

 ε

. In

AING, ε

is slowly decreasing proportion-

ally to the number of data-points associated to y

i.e. the more y

learns, the more it becomes sta-

ble, and ε

is simply heuristically set to 100 times

smaller than the actual value of ε

(i.e. ε

 ε

)

• Each time a data-point is assigned to a winning

neuron y

, the age of edges emanating from this

neuron is increased (line 14 of Algorithm 1).

Let n

max

the maximum number of data-points as-

signed to a neuron. A given edge is then consid-

ered ”old” and thus removed (line 19 of Algorithm

1) if its age becomes higher than n

max

. Note that

this is not an externally-set parameter, it is the cur-

rent maximum number of data-points assigned to

a neuron among the existing ones.

4 EXPERIMENTAL EVALUATION

4.1 Experiments on Synthetic Data

In order to test AING’s behaviour, we perform an ex-

periment on artiﬁcial 2D data of 5 classes (Figure

AnAdaptiveIncrementalClusteringMethodbasedontheGrowingNeuralGasAlgorithm

Algorithm 1: AING Algorithm (up bound).

1: init graph G with the two ﬁrst coming data-points

2: κ = 0

3: while some data-points remain unread do

4: get next data-point x, update

d accordingly

5: let y

, y

the two nearest neurons from x in G

6: get T

and T

according to formula 1

7: if dist(x,w

) > T

then

8: G ← G ∪ {y

new

= x}

9: else

10: if dist(x,w

) > T

then

11: G ← G ∪ {y

new

= x}

12: connect y

new

to y

by an edge of age 0

13: else

14: increase the age of edges emanating

from y

15: let ε

,ε

100×|X

16: w

+ = ε

× (x − w

)

17: w

+ = ε

× (x − w

),∀y

∈ V

18: connect y

to y

by an edge of age 0

19: remove old edges from G if any

20: end if

21: end if

22: while number of neurons in G > up bound do

23: κ = κ +

24: G ← Merging(κ, G)  call Algorithm 2

25: end while

26: end while

4(a)) composed of a Gaussian cloud, a uniform dis-

tribution following different shapes, and some uni-

formly distributed random noise. Figure 4(b) and 4(c)

show the topology of neurons obtained without using

the merging process (up bound = +∞), whereas for

Figure 4(d) and 4(e), the merging process was also

considered. However, for Figure 4(b) and 4(d), the

data were given to AING class by class in order to

test the incremental behaviour of AING. The results

show that AING perfectly learns the topology of data

and conﬁrms that it has good memory properties. On

the other hand, for Figure 4(c) and 4(e) the arrival or-

der of data was random. The results show that AING

performs well, even if the arrival order of data is ran-

dom.

4.2 Experiments on Real Datasets

We consider in our experimental evaluation, AING

with and without the merging process

, some main

incremental neural clustering algorithms, and an ac-

We will refer to AING without the merging process by

AING1, and to AING with the merging process by AING2

Algorithm 2: Merging (κ, G).

1: init

G with two neurons chosen randomly from G

2: for all y ∈ G do

3: let ˜y

, ˜y

the two nearest neurons from y in

4: let d

= dist(w

˜y

),d

= dist(w

˜y

)

5: if random

uni f orm

([0,1]) < min(

×d

,1) then

G ←

G ∪ { ˜y

new

˜y

new

= w

}

7: else

8: if random

uni f orm

([0,1]) < min(

×d

,1) then

G ←

G ∪ { ˜y

new

˜y

new

= w

}

10: connect ˜y

new

to ˜y

by an edge of age 0

11: else

12: increase age’s edges emanating from

˜y

13: Let ε

˜y

,ε

100×|X

˜y

14: w

˜y

+ = ε

× (w

− w

˜y

)

15: w

˜y

+ = ε

× (w

− w

˜y

),∀˜y

∈ V

˜y

16: connect ˜y

to ˜y

by an edge of age 0

17: remove old edges from

G if any

18: end if

19: end if

20: end for

21: return

curate incremental Kmeans (Shindler et al., 2011) as

a reference in comparing the results.

We consider a total of six datasets of different

size and dimensions. Three standard public hand-

written digit datasets (i.e. Pendigit and Optdigit from

the UCI repository (Frank and Asuncion, 2010), and

Mnist dataset (LeCun Yann, 2010)), and three dif-

ferent datasets of documents represented as bag of

words, taken from a real administrative documents

processing chain:

• Pendigit: 7494 data for learning, 3498 data for testing,

17 dimensions, 10 classes.

• Optdigit: 3823 data for learning, 1797 for testing, 65

dimensions, 10 classes.

• Mnist: 60000 data for learning, 10000 for testing, 784

dimensions, 10 classes.

• 1

documentary dataset: 1554 data for learning, 777

for testing, 272 dimensions, 143 classes.

• 2

documentary dataset. 2630 data for learning, 1315

for testing, 278 dimensions, 24 classes.

• 3

documentary dataset. 3564 data for learning, 1780

for testing, 293 dimensions, 25 classes.

In addition to the number of produced representa-

tives and the number of required parameters, we con-

sider as evaluation measures the recognition rate (R)

and the v-measure (V) (Rosenberg and Hirschberg,

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

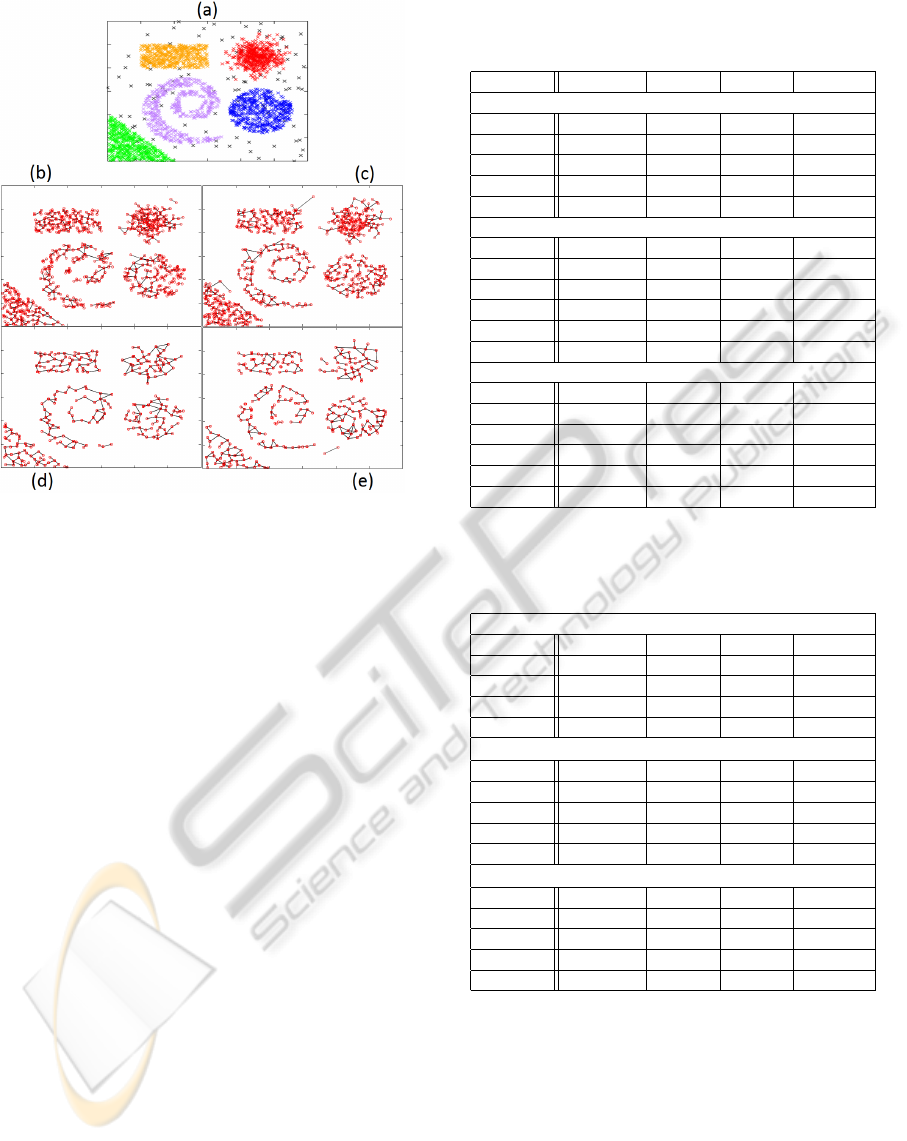
Figure 4: The built topology of activated neurons, with and

without the merging process.

2007). Basically, v-measure is an entropy-based mea-

sure which expresses the compromise between ho-

mogeneity and completeness of the produced clus-

ters and gives an idea about the ability to generalize

to future data. Indeed, according to (Rosenberg and

Hirschberg, 2007), it is important that clusters contain

only data-points which are members of a single class

(perfect homogeneity), but it is also important that all

the data-points that are members of a given class are

elements of the same cluster (perfect completeness).

For each algorithm, we repeat many experiments

by slightly varying the parameter values needed by

each of them. We ﬁnally keep the parameter values

matching the best clustering results according to the

considered evaluation measures.

The results obtained on the 3 ﬁrst datasets

are shown in Table 1, where AING1 (respectively

AING2) refers to AING without (respectively with)

the merging process. From table 1 we see that con-

cerning the 1

dataset, Kmeans achieves a better

v-measure, and maintains fewer representatives, but

does not reach a recognition rate which is compara-

ble to the other algorithms. Although AING1 (with-

out the merging process) is independent of external

parameters, it realises almost the same recognition

rate and v-measure as SOINN and I2GNG. AING2

(with the merging process) produces fewer neurons

and the recognition rate as well as the v-measure

are improved further. Concerning the 2

dataset

(Optdigit), AING1 realises the greatest performances.

Table 1: Validation on public standard datasets (R = Recog-

nition rate, V = V-Measure, Params = Number of parame-

ters).

Method Neurons R % V % Params

Pendigit dataset

AING1 1943 97.427 52.538 0

AING2 1403 97.827 53.624 1

Kmeans 1172 97.055 54.907 3

SOINN 1496 97.341 52.222 3

I2GNG 2215 97.541 52.445 4

Optdigit dataset

Method Neurons R % V % Params

AING1 1371 97.718 54.991 0

AING2 825 97.440 55.852 1

Kmeans 1396 97.495 52.899 3

SOINN 1182 96.82 53.152 3

I2GNG 1595 97.161 53.555 4

Mnist dataset

Method Neurons R % V % Params

AING1 3606 94.06 45.258 0

AING2 2027 94.21 46.959 1

Kmeans 2829 94.04 45.352 3

SOINN 2354 93.95 44.293 3

I2GNG 5525 94.10 43.391 4

Table 2: Validation on datasets of administrative documents

(R = Recognition rate, V = V-Measure, Params = Number

of parameters).

documentary dataset

Method Neurons R % V % Params

AING1 1030 91.505 87.751 0

Kmeans 1013 90.862 86.565 3

SOINN 1045 88.545 87.375 3

I2GNG 1367 91.119 86.273 4

documentary dataset

Method Neurons R % V % Params

AING1 1215 98.251 57.173 0

Kmeans 1720 98.098 53.966 3

SOINN 1650 97.338 55.124 3

I2GNG 1846 98.403 54.782 4

documentary dataset

Method Neurons R % V % Params

AING1 2279 91.685 60.922 0

Kmeans 2027 91.179 60.192 3

SOINN 2437 88.707 61.048 3

I2GNG 2618 90.393 60.954 4

With AING2, the number of neurons is consider-

ably reduced and a better compromise between ho-

mogeneity and completeness is achieved. The recog-

nition rate is a little worse than the AING1, but still

very close to the highest rate obtained by the other

algorithms. Concerning the Mnist dataset, AING2

achieved the best performances.

Table 2 shows the results obtained on the docu-

mentary datasets. AING is used without the merging

process (AING1) because the datasets are not very

AnAdaptiveIncrementalClusteringMethodbasedontheGrowingNeuralGasAlgorithm

large (up bound is just omitted by setting its value

to +∞). Roughly, we can make the same conclusions

as with the previous datasets. AING1 performs well,

although it does not require other pre-deﬁned param-

eters.

Figure 5: The recognition rate achieved by AING according

to the parameter up bound (for the Pendigit dataset).

Figure 5 shows how the recognition rate changes

with changing values of the upper bound parameter

(up bound) for the ﬁrst dataset. We can observe that

for all values greater than or equal to 600 (i.e. most

reasonable values that up bound can take), the recog-

nition rate is in [97,98] (i.e. around the same value).

Note that for two experiments with a ﬁxed value of

up bound, the result may slightly be different since

the merging process is probabilistic. Furthermore,

the maximum number of neurons that can be gen-

erated for this example is 1943, thus, for values of

up bound in [1943, +∞[, the merging process does not

take place and AING2 performs exactly like AING1

(i.e. for AING on the Pendigit dataset ∀ up bound ∈

[1943,+∞[: R = 97.4271%).

Furthermore, the time required to incrementally

integrate one data-point is strongly related to the cur-

rent number of neurons because the search for the

nearest neurons from a new data-point is the most

consuming operation. Figure 6 shows that AING is

more convenient for a long-life learning task since it

maintains a better processing time than the other al-

gorithms over long periods of time learning, thanks

to the merging process. The overall running time for

the Mnist dataset (i.e. required for all the 60000 data-

points) is 1.83 hours for AING, 2.57 hours for SOINN

and 4.49 hours for I2GNG.

5 CONCLUSIONS AND FUTURE

WORK

This paper presents an incremental clustering method

which incrementally processes data from the data

Figure 6: The average time (in milliseconds) required to in-

crementally integrate one data-point (for the Mnist dataset).

stream, without being sensitive to initialization pa-

rameters. It initially decides whether a new data-

point should produce a new cluster representative by

means of a parameter-free adaptive threshold asso-

ciated to each existing representative, and evolving

dynamically according to the data and the topology

of neurons. Some representatives may eventually

be assigned to others by means of a distance-based

probabilistic criterion each time their number exceed

a speciﬁed limit; thus, maintaining a better clusters

completeness, and preserving time and memory re-

sources.

Nonetheless, further work still needs to be done.

One of our directions for future work is to provide

some theoretical worst-case bounds on memory and

time requirement, and allow the algorithm to auto-

matically determine an appropriate upper bound for

the number of representatives; this will allow AING

to perform a long-life learning. Then, we want to inte-

grate the algorithm in a case-based reasoning system

for document analysis, whose case-base will be con-

tinuously maintained by the AING algorithm.

REFERENCES

Aggarwal, C. C., Han, J., Wang, J., and Yu, P. S. (2003). A

framework for clustering evolving data streams. Pro-

ceedings of the 29th international conference on Very

large data bases, pages 81–92.

Chen, Y. and Tu, L. (2007). Density-based clustering for

real-time stream data. International Conference on

Knowledge Discovery and Data Mining, pages 133–

142.

Frank, A. and Asuncion, A. (2010). The uci machine learn-

ing repository. http://archive.ics.uci.edu/ml/.

Fritzke, B. (1995). A growing neural gas network learns

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

topologies. Neural Information Processing Systems,

pages 625–632.

Hamza, H., Belaid, Y., Belaid, A., and Chaudhuri, B.

(2008). Incremental classiﬁcation of invoice docu-

ments. International Conference on Pattern Recog-

nition, pages 1–4.

Keogh, E., Lonardi, S., and Ratanamahatana, C. A. (2004).

Towards parameter-free data mining. Proceedings of

the 10th International Conference on Knowledge Dis-

covery and Data Mining, pages 206–215.

LeCun Yann, C. C. (2010). MNIST handwritten digit

database. http://yann.lecun.com/exdb/mnist/.

Martinetz, T. (1993). Competitive hebbian learning rule

forms perfectly topology preserving maps. ICANN,

pages 427–434.

O’Callaghan, L., Meyerson, A., Motwani, R., Mishra, N.,

and Guha, S. (2002). Streaming-data algorithms for

high-quality clustering. In ICDE’02, pages 685–685.

Prudent, Y. and Ennaji, A. (2005). An incremental growing

neural gas learns topology. European Symposium on

Artiﬁcial Neural Networks.

Rosenberg, A. and Hirschberg, J. (2007). V-measure: A

conditional entropy-based external cluster evaluation

measure. NIPS, pages 410–420.

Shen, F., Ogura, T., and Hasegawa, O. (2007). An enhanced

self-organizing incremental neural network for online

unsupervised learning. Neural Networks, pages 893–

903.

Shindler, M., Wong, A., and Meyerson, A. (2011). Fast

and accurate k-means for large datasets. NIPS, pages

2375–2383.

AnAdaptiveIncrementalClusteringMethodbasedontheGrowingNeuralGasAlgorithm