A Hybrid Intuitionistic MCDM Model for Supplier Selection

Babak Daneshvar Rouyendegh (Babek Erdebilli)

Department of Industrial Engineering, Atılım University, P.O. Boran x 06836, İncek, Ankara, Turkey

Keywords: Supply Chain Management (SCM), Analytic Hierarchy Process (AHP), Intuitionistic Fuzzy Topsis (IFT),

Supplier Selection.

Abstract: This paper gives an overview of the Analytic Hierarchy Process (AHP) and Intuitionistic Fuzzy TOPSIS

(IFT) methods. This study deals an evaluation methodology based on the AHP-IFT where the uncertainty is

handeled with linguistic values. First, the supplier selection problem is formulated by AHP is used to

determine weights of the criteria. In the second stage, IFT used to obtain full ranking among alternatives

based on opinion of the Decision Makers (DMs). The present model provides an accurate and easy

classification in supplier attributes by that have been prioritized in the hybrid model. A numerical example

is given to clarify the main developed result in this paper.

1 INTRODUCTION

Selection a suitable supplier among different

suppliers is an important matter for supply chain

management (SCM). Selecting the right suppliers

reduces the purchasing cost, quality problems, and

long-lead times and definitely improves corporate

competitiveness (Vokurka et al., 1998; Humphreys

et al., 2007; Rouyendegh and Erkan, 2012). The

most important part of the SCM is the purchasing

activity, and the multi-criteria analysis appears to be

the right solution for the classification of many

purchased goods in the firm as the effort to obtain

products at a reasonable cost, in the right quantity,

the appropriate quality, at the right time from the

right source, is quite crucial for a firm’s survival at

the market (Simchi-Levi et al., 2003). Beside,

suppliers have a significant impact on the quality,

cost and leadtime of new products and technologies

needed to meet new and emerging market demands

(Rouyendegh and Erkan, 2012;).

In this study, a hybrid model for supplier

evaluation and a selection based on cost, quality,

flexibility, delivery, and variety are used in the

AHP-IFT hybrid model. The model quantifies five

multiple criteria in AHP to combine them into one

global variable for decision-making. To do that, we

first present the concept of AHP and determine the

weight of criteria based on opinion of Decision

Makers (DMs). Then, we introduce the concept of

IFT and develop model based on opinion of the

DMs. A numerical example is also presented to

better illustrate the model.

2 BASIC CONCEPT OF IFS

The following, briefly introduce some necessary

introductory basic concepts of IFS. IFS A in a finite

set R can be written as:





 

,(),()

( ) : ( ) 0 ,1 , 0 ,1

Ar rvrrR

where

rr R

vr vr R









(1)

are membership function and non-membership

function, respectively, such that

0()()1

rvr rR











0,1R 

(2)

A third parameter of IFS is

()



, known as the

intuitionistic fuzzy index or hesitation degree of

whether r belongs to A or not

() 1 () ()

AAA

rrvr









(3)

()



is called the degree of indeterminacy of r to

A it is obviously seen that for every

rR

0()1





If the

()



(4)

It is small, knowledge about r is more certain. If

()



is great, knowledge about r is more

uncertain. Obviously,

519

Daneshvar Rouyendegh B..

A Hybrid Intuitionistic MCDM Model for Supplier Selection.

DOI: 10.5220/0004257405190522

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 519-522

ISBN: 978-989-8565-39-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

When

() 1 ()

rvr





(5)

For all elements of the universe, the ordinary

FST concept is recovered (Boran et.al., 2012).

Let A and B are IFSs of the set R, then multiplication

operator is defined as follows (Atanassov, 1986).





(). (), () () (). ()

ABA B AB

AB r rvr vr vrvrr R



   

(6)

3 AHP- IFT

To rank a set of alternative, the AHP-IFT

methodology as outranking relation theory was used

to analyze the data of a decision matrix. We assume

m alternatives and n decision criteria. Each

alternative is evaluated with respect to the n criteria.

All the values assigned to the alternatives with

respect to each criterion form a decision matrix.

In this study, our model integrates two, well –

known models, AHP and IFT methods. The

evaluation of the study based on this hybrid

methodology given in Figure 1. The procedure for

AHP- IFT methodology ranking model has been

given as follows:

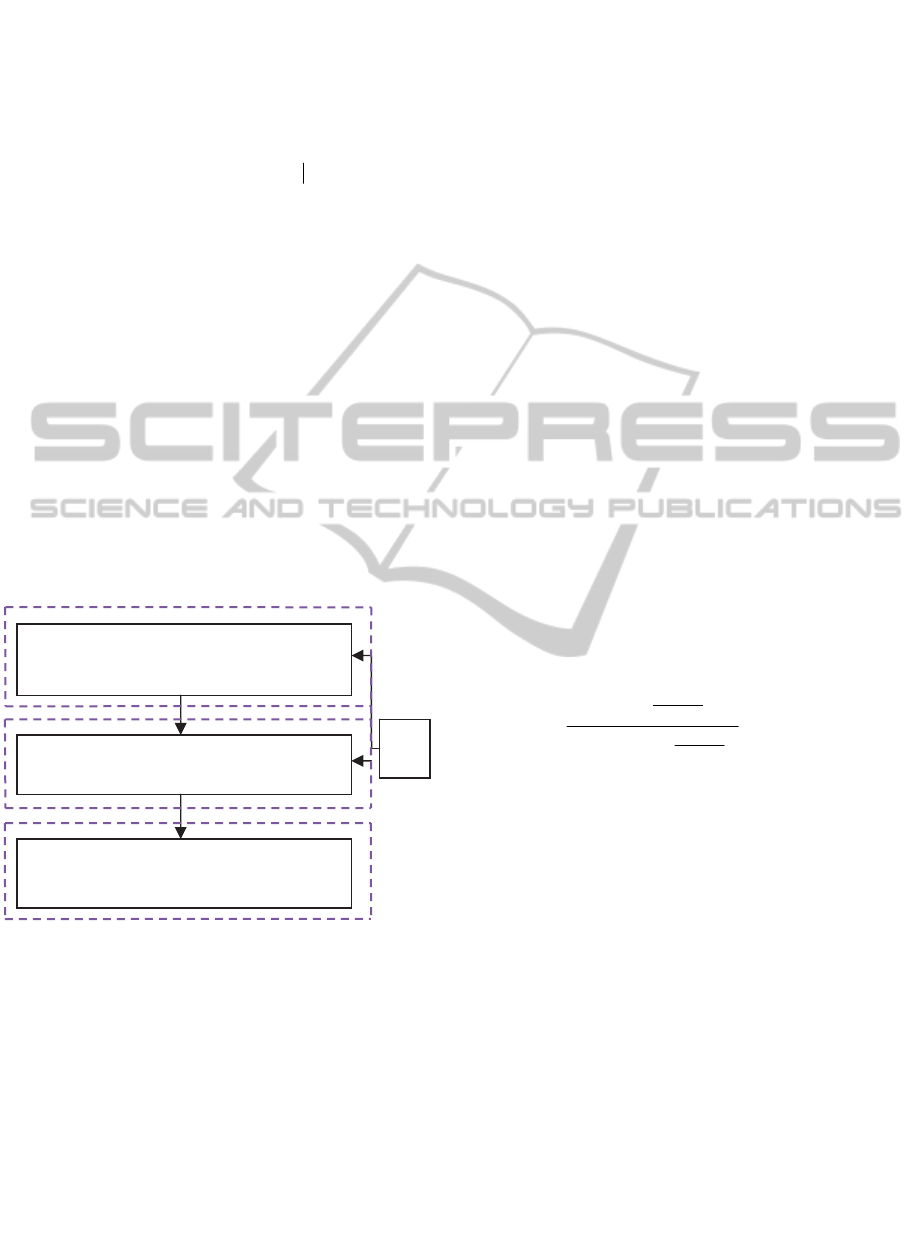
Figure 1: Schematic diagram of the AHP–IFT

methodology.

Let A = {A

, A

, … , A

} be a set of alternatives

and C = {C

, C

, … , C

} be a set of criteria, it

should be mentioned here that the presented

approach mainly utilizes the IFT method presented

in (Boran et.al., 2009; Boran, 2011; Rouyendegh

2012; Shyur, 2006; Xu, 2007d). We modify the

selection process to a nine-step, AHP-IFT hybrid

procedure, presented as follows:

Step 1. Identify the Alternative

In the first step, we provide a list of projects denoted

by A = {A

, A

, … , A

}

Step 2. Identify the criteria.

The criteria could be denoted by

C = {C

, C

, … , C

}. Identification of criteria,

recognition of the relationship between criteria.

Step 3. Determine the weight of criteria based on the

opinion of decision makers (Wi).

We assume that decision group contains l = {

, l

, … , l

}DMs. The decision group or decision

makers are given the task of forming individual pair-

wise comparisons by using standard scale of nine

levels.

Both distances from each DM can be aggregated

as the distances of the group by taking geometric

mean:

( ) 1,...,

iij

Dim







(7)

Step 4. Determine the weights of importance of

DMs:

In this step, we assume that decision group

contains l = { l

, l

, … , l

} DMs. The importance of

the DMs is considered as linguistic terms. These

linguistic terms were assigned to IFN. Let

= [μ

, ν

, π

] be an intuitionistic fuzzy number for

rating of kth DM. Then the weight of lth DM can be

calculated as:



(())

0,1 1.

where and































(8)

Step 5. Determine Intuitionistic Fuzzy Decision

Matrix (IFDM).

Based on the weight of DMs, the aggregated

intuitionistic fuzzy decision matrix (AIFDM) was

calculated by applying intuitionistic fuzzy weighted

averaging (IFWA) operator (Xu, 2007d). In group

decision-making process, all the individual decision

opinions need to be fused into a group opinion to

construct AIFDM.

Let

() ()

()

ij m n





is an IFDM of each DM.

λ = {λ

, λ

, … , λ

} is the weight of DM.

()

ij m n





Where

(1) (2) ( ) (1) ( 2) (3) ( )

12 3

( , ,..., ) ...

ij ij ij ij ij ij ij k ij

rIFWArr r r r r r



  



(9)

Determine the weight of criteria via AHP

Determine the weight of alternatives via

IFT

The calculation of S= R*W and Determine

the final rank

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

520

() () () ()

111 1

1(1 ),(),(1 ) ()

ll l l

kkk k

ll l l

ij ij ij ij

lll l

  



 



   





 

Step 6. The calculation of S= R*Wi

The weights of criteria (Wi) with respect to

IFDM (R) is defined as follows:

S=R*Wi (10)

Step 7. Determine intuitionistic fuzzy positive and

negative ideal solution:

In this step, the intuitionistic fuzzy positive ideal

solution (IFPIS) and intuitionistic fuzzy negative

ideal solution (IFNIS) have to be determined. A

IFPIS and A

−

is IFNIS. Then A

and A

−

are equal to:

*** ** ***

( , ,..., ), ( , , ), 1,2,...,

nj jjj

rr r r v j n





    



(11)

and

( , ,..., ), ( , , ), 1,2,...,

nj jjj

rr r r v j



  



   



(12)

Where

 

(max ),(min ,

jij ij

JjJ

 





 

 







(13)

 

(min ),(max ,

jij ij

vvjJvjJ







 







(14)

   

(1 max mi n ) , (1 min max ,

jijij ijij

vjJ vjJ

 





 

     







(15)

 

(min ),(max ,

jij ij

JjJ

 







 

 







(16)

 

(max ),(min ,

jij ij

vvjJvjJ







 

 







(17)

   

(1 min max ), (1 max mi n .

jijij ijij

vjJ vjJ

 







 

     







(18)

Step 8. Determine the separation measures between

the alternative:

Separation between alternatives on IFS, distance

measures proposed by (Atanassov, 1999) including

the generalizations of Hamming distance, Euclidean

distance and their normalized distance measures can

be used. After selecting the distance measure, the

separation measures, S

and S

, of each alternative

from IFPIS and IFNIS, are calculated.

****

iijjijjijj

Svv

 





  







(19)

iijjijjijj

Svv

 



 



















(20)

Step 9. Determine the final ranking

In the final step, the relative closeness

coefficient of an alternative is defined as follows:

01.

CwhereC









(21)

4 NUMERICAL EXAMPLE

In this section, we will describe how an AHP- IFT

hybrid model was applied via an example. Criteria

to be considered in the supplier selections are

determined by the expert team from a decision

group. In our study, we employ five evaluation

criteria. The attributes which are considered here in

assessment of A

(i=1,2,3) are: C

,.., C

. The

committee evaluates the performance of alternatives

(i=1,2,3) according to the attributes C

(j=1,2,…,5) respectively. After preliminary

screening, three alternatives A1, A

, and A

, remain

for further evaluation. A team of four DMs such as;

, DM

, and DM

has been formed to select the

most suitable alternative. Criteria to be considered in

the supplier’s selection are determined by DMs team

from University Procurement Department. There

five criteria are as follows: (C1) Cost (C2) Quality

(C3) Payment Flexibility (C4) Delivery (C5)

Variety.

Now utilize the proposed AHP- IFT hybrid

model to prioritize alternatives, the following steps

were taken:

After the weights of the criteria and the rating of

the alternatives were determined, the aggregated

weighted IFD, IFPIS and IFNIS. Negative and

positive separation measures based on normalized

Euclidean distance for each alternative and the

relative closeness coefficient were calculated in

Table 1.

Table 1: Separation measures and the relative closeness

coefficient of each alternative.

Alternative

−

2.019 2.318 0.533

2.031 2.022 0.467

2.237 2.181 0.494

A numerical example was illustrated the result as

follow: Among 3 alternatives with respect to 5

criteria, after using this methodology, the best one is

AHybridIntuitionisticMCDMModelforSupplierSelection

521

alternative 1 and alternative 3, alternative 2 will

follow it respectively.

5 CONCLUSIONS

In this paper, we present a hybrid model using both

AHP and intitionistic fuzzy TOPSIS (IFT) models

for supplier selection under fuzzy environment to

account for vagueness and uncertainty. In the

evaluation process, the ratings of each alternative,

given with intitionistic fuzzy information, were

represented as IFNs. In this hybrid model, AHP is

used to assign weights to the criteria, while IFT is

employed to calculate the full-ranking of the

alternatives. The AHP-IFT hybrid model was used

to aggregate the rating of DMs. Multiple DMs are

often preferred rather than a single DM to avoid the

minimize the partiality in the decision process.

Therefore, group decision making process for

alternative selection is very useful. The presented

approach not only validates the methods, but also

considers a more extensive list of criteria, suitable

for supplier selection. The AHP-IFT hybrid model

has capability to deal with similar types of the same

situations.

REFERENCES

Atanassov, K. T., 1986. Intuitionistic fuzzy sets. Fuzzy

Sets and Systems. Vol.20, pp. 87–96.

Atanassov, K.T., 1999. Intuitionistic fuzzy sets. Springer,

Heidelberg.

Boran, F. E., Genç, S., Kurt, M., & Akay, D., 2009. A

multi-criteria intuitionistic fuzzy group decision

making for supplier selection with TOPSIS method.

Expert Systems with Applications. 36(8), pp. 11363-

11368.

Boran, F. E., 2011. An integrated intuitionistic fuzzy

Multi-Criteria Decision-Making method for facility

location selection. Mathematical and Computational

Applications. 16(2) pp.487-496.

Boran, F. E., Boran, K., Menlik, T., 2012. The evaluation

of renewable energy technologies for electricity

generation in Turkey using intuitionistic fuzzy

TOPSIS. Energy Sources, Part B: Economics,

Planning and Policy. 7, 81-90.

Humphreys, P., Huang, G., Cadden, T., and Mcivor, R.

2007. Integrating design metrics within the early

supplier selection process. Journal of Purchasing and

Supply Management, 13, pp.42–52.

Rouyendegh, B.D., Erkan, T. E., 2012. Selection the Best

Supplier Using AHP Method. African Journal of

Business Management. 6(4), pp.1455-1462.

Rouyendegh, B. D., 2012. Evaluating Projects Based on

Intuitionistic Fuzzy Group Decision Making. Journal

of Applied Mathematics. Vol. 2012, 16 pages,

doi:10.1155/2012/ 824265.

Shyur, H. J., Shih, H. S., 2006. A hybrid MCDM model

for strategic vendor selection. Mathematical and

Computer Modelling. 44( 7-8), pp. 749-761.

Simchi-Levi, D., Kaminsky, P., 2003. Designing and

Managing Supply Chain. McGraw-Hill Higher

Education, Second Edition.

Vokurka, R. J., Fliedner, G. J., 1998. The journey toward

agility. Industrial Management & Data Systems. 98

(4), pp.165–171.

Xu, Z. S., 2007d. Intuitionistic fuzzy aggregation

operators. IEEE Transaction of Fuzzy Systems. 15 (6),

pp. 1179–1187.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

522