A Study on Generation of Synthetic Evolving Social Graph

Nagehan Ilhan and S¸ule G¨und¨uz

O˘g¨ud¨uc¨u

Department of Computer Engineering, Istanbul Technical University, Istanbul, Turkey

Keywords:

Evolving Social Network, Synthetic Data Generation.

Abstract:

Social networks are popular tools for communication, interaction, and information sharing on the Internet.

The extreme popularity and rapid growth of these online social networks reveal to study, understand, and

discover their properties. Social networks evolve gradually and the network structure varies as the network

grows. Large-scale dynamic network analysis requires a large quantity of network data to be available for

the experiments and using real data have restrictions due to the privacy issues. Synthetic data generation

is an alternative way to overcome these problems. The challenge when generating synthetic data is having

characteristics that are similar to real-world data. In this paper, we study on generating synthetic, but realistic,

time-evolving social graphs. We describe two main classes of properties: static and dynamic. We analyzed

real datasets and extracted their behavior using static and dynamic properties. Then, we generated synthetic

graphs with different parameter settings using Barabasi-Albert model (Barabasi and Albert, 1999). Our work

enables the creation of synthetic networks that reﬂect both static and dynamic characteristics of online social

networks. Moreover, our generated data may lead to more accurate structural and growth models, which are

useful for network analysis and planning.

1 INTRODUCTION

The popularity of online social networks has in-

creased the interest in analyzing how these networks

evolve over time. One fundamental question is to un-

derstand how do the network properties change as the

network evolves. In recent years a wide variety of

models have been proposed to analyze the evolution

of complex networks. The big proportion of the sig-

niﬁcant amount of the network data that are being col-

lected are often about people and contain personal in-

formation. When such data are being analyzed and

mined, publishing the data becomes important prob-

lem due to the privacy issues. Furthermore, time to

time the limited number of available network graphs

are insufﬁcient to generate meaningful experimental

results.

An alternative approach, is to use synthetically

generated data. Albeit the challenges, the use of syn-

thetic data offers great opportunities. The user can

control and rapidly generate the data set with the de-

sired characteristics, size and quality. It allows the

user to investigate what-if scenarios when real data

are difﬁcult to collect. The generated data can be

shared, and thus allow other researchers to repeat ex-

periments and compare algorithms.

The main challenge in generation of synthetic data

is its realism. It is not easy to create data with charac-

teristics that are similar to real-world data. The gener-

ated data should obey all the main static patterns that

have appeared in the literature and also obey the re-

cently discovered temporal evolution patterns.

A widespread model that used to simulate social

networks is Barabasi-Albert model (Barabasi and Al-

bert, 1999). In this paper, we generate different evolv-

ing synthetic graphs with distinct parameters using

Barabasi-Albert model, compute static and dynamic

graph metrics of the generated synthetic graphs and

compare them with the measurements of the real so-

cial networks. Thereby, we explore the most conve-

nient parameter settings to generate synthetic graphs

that best ﬁt to the real networks. Our study is useful

in generating synthetic networks that obey static and

dynamic properties of social networks. Our generated

networks can be used as better structural and growth

models in social network analysis.

The paper is organized as follows: in Section 2

previous works on graph generation are given. Static

and dynamic properties and Barabasi-Albert model

explained in Section 3. Measurements and results of

the generated and real graphs are given in Section 4.

Finally, we conclude the paper.

523

Ilhan N. and Gündüz Ö

güdücü ¸S..

A Study on Generation of Synthetic Evolving Social Graph.

DOI: 10.5220/0004258005230526

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 523-526

ISBN: 978-989-8565-39-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

Building synthetic social graphs that are sufﬁciently

representative of real world social graphs has been

of interest for researchers for a long time. Most of

the studies try to extract the characteristics of graphs

and the patterns that can help to distinguish between

an actual real-world graph and any synthetic one.

As summarized in (Chakrabarti and Faloutsos, 2006),

there exist several patterns: power laws, small diame-

ters and community effects which together character-

ize the graphs.

One of the ﬁrst models has been proposed by

(Erd¨os and R´enyi, 1959) which employs random net-

works in order to generate real networks. Random

graphs are generated by picking nodes under some

random probability distribution and then connecting

them by edges. Watts and Strogatz came up with a

model that starts with a regular ring of n nodes where

each node is connected to its k closest neighbours and

than the nodes are rewired according to some prob-

ability to another node chosen uniformly at random

(Watts and Strogatz, 1998). It has high clustering co-

efﬁcient unlike Erdos-Renyi but fails to reproduce the

power-law distribution of the degrees and behave like

a Poisson distribution. It is clear that purely random

graphs are not a good approximation of topology of

social networks despite showing small-world effect.

Studying the static snapshots of graphs has led

to analyzing properties such as the small-world

phenomenon (Travers and Milgram, 1969) and the

power-law degree distributions. However, in time-

evolving graphs interesting properties have been dis-

covered, such as shrinking diameters, and densiﬁca-

tion power law. The Forest Fire model attempts to ex-

plain the densiﬁcation and decreasing-diameter over

time and also captures the power-law degree distribu-

tion (Leskovec et al., 2005b).

Real networks are often scale-free networks inho-

mogeneous in degree, having hubs and a scale-free

degree distribution. Such networks are better to be

represented by the preferential attachment family of

models, such as the BarabasiAlbert model (Barabasi

and Albert, 1999). It produces graphs with power-law

degree distributions missing from random graphs. It

captures two shared mechanisms shared by many real

networks: incremental growth and preferential attach-

ment properties.

The authors in (Leskovec et al., 2005a),(Leskovec

and Faloutsos, 2007) proposed the Kronecker model

which is based on Kronecker multiplication to gen-

erate graphs that obey the properties of real graphs.

Kronecker model starts with the initial seed graph and

constructs a larger graph by repeatedly multiplying

the seed graph with itself. It creates the target graph

by multiplying with a seed graph. It is another well

known technique to generate scale-free graphs. How-

ever, the ﬁnal graph generated with the Kronecker

multiplication method heavily depends on the initial

seed graph. Thus, difﬁcult to conﬁgure or control

to obtain a graph with desired properties. Barabasi-

Albert method with preferential attachment is conﬁg-

urable and generates much better representative net-

works for real-world despite some lacks.

3 DATA GENERATION

3.1 Data Representation

A social graph G(V, E), made of nodesV and edges E

that connect nodes with different relationships. In this

study, real evolving graph G described over a time pe-

riod [0..T] and it will be decomposed into a sequence

of static snapshots G

[0,ε]

, ...., G

[T−ε,T]

= G

, ..., G

. ε

is the discretization factor which will be adjusted de-

pending on the granularity of the time stamps and

t,t+ε

is the graph containing all nodes and edges in-

volved during the time period [t, t + ε].

3.2 Barabasi-Albert Model

Barabasi-Albert incorporates two main properties of

the of scale-free networks: incremental growth and

preferential attachment (Barabasi and Albert, 1999).

These properties also shared by many real networks.

Real world networks expand in size continuously by

the addition of new nodes (incremental growth) and

new nodes preferentially attach to nodes with a high

degree(preferential attachment). The model has three

parameters: n is the number of nodes, m is the number

of edges to add in each step and power is the power

of the preferential attachment.

3.3 Graph Properties

In this study, we describe two main classes of prop-

erties of graphs that represent social networks. Static

properties, describe the structure of snapshots of the

graphs. Radius, diameter, clustering coefﬁcient

and degree distribution metrics will be considered.

Dynamic properties such as shrinking diameter and

densiﬁcation power-law are observed over a period

of time and evaluate howmeasurements of these snap-

shots change by looking the series of static snaphots.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

524

4 EXPERIMENTAL RESULTS

4.1 Dataset Description

Our experimentation has been conducted on dis-

tinct synthetic and real datasets. Three distinct real

datasets: Internet Link, Flickr (Mislove et al., 2008)

and Youtube (Mislove, 2009) consisting different

size, volume and clustering coefﬁcient degrees has

been used. Weekly snapshots are taken from real

datasets and evolution of ten time period has been

taken into account. Each synthetic dataset has been

created using Barabasi-Albert model with distinct m

and power parameters. Graphs created with the same

number of initial nodes n of the Internet Link dataset

(Mislove, 2009) and evolved over ten time period by

adding random number of nodes between 2000 and

3000 at each period. Table 1 gives the ultimate num-

ber of nodes and edges of the datasets after tenth evo-

lution which are used in the study. Synthetic datasets

represented with the SD abbreviation in the table.

Table 1: Datasets.

Datasets Nodes Edges

Internet Link 22084 122439

Flickr 2263928 13982994

Youtube 1637838 7778675

SD1 (m=2 power=1) 32567 65131

SD2 (m=2 power=1.4) 30780 61557

SD3 (m=2 power=2) 33826 67649

SD4 (m=3 power=1) 34237 102705

SD5 (m=3 power=1.4) 31823 95463

SD6 (m=3 power=2) 32464 97386

SD7 (m=10 power=1) 31457 314515

Table 2: Radius,diameter and clustering coefﬁcient of the

studied networks.

Dataset Radius Diameter Clustering Coefﬁcient

Flickr 13 27 0.366

Youtube 13 21 0.177

Internet Link 1 12 0.008

SD1 (m=2 power=1) 6 10 0.001

SD2 (m=2 power=1.4) 3 6 0.758

SD3 (m=2 power=2) 2 4 0.998

SD4 (m=3 power=1) 5 8 0.001

SD5 (m=3 power=1.4) 3 5 0.527

SD6 (m=3 power=2) 2 3 0.998

SD7 (m=10 power=1) 3 5 0.010

4.2 Results of Static Properties

Radius and Diameter. Table 2 shows the results of

the radius and average diameter values of the graphs

after tenth evolution. The average diameter is calcu-

lated by taking the mean of the average shortest path

lengths over all nodes. Our real and synthetic graphs

are found to exhibit small diameter property despite

Figure 1: Degree Distributions.

their large population. The datasets SD3 and SD6

have smaller radius and diameter values since they are

denser compared to other graphs because of having

greater power value.

Clustering Coefﬁcient. Our clustering coefﬁcient re-

sults have shown on Table 2. Our real social networks

do not have high clustering coefﬁcient value as it is

expected. Nevertheless, clustering coefﬁcient degree

of synthetic datasets increase as the power value in-

crease. SD3 and SD6 have the maximum clustering

coefﬁcient degrees due to the power.

Degree Distribution. The results have shown in

Figure 1. We can see from the results in Figure

1 that the synthetic datasets that are generated with

slighter preferential attachment power value (power)

ﬁt power-law scaling more than the datasets generated

with greater power value. Higher preferential attach-

ment power value results several hub nodes while the

rest of the nodes in the network having few connec-

tions. Consequently, SD3 and SD6 do not ﬁt power-

law scaling.

AStudyonGenerationofSyntheticEvolvingSocialGraph

525

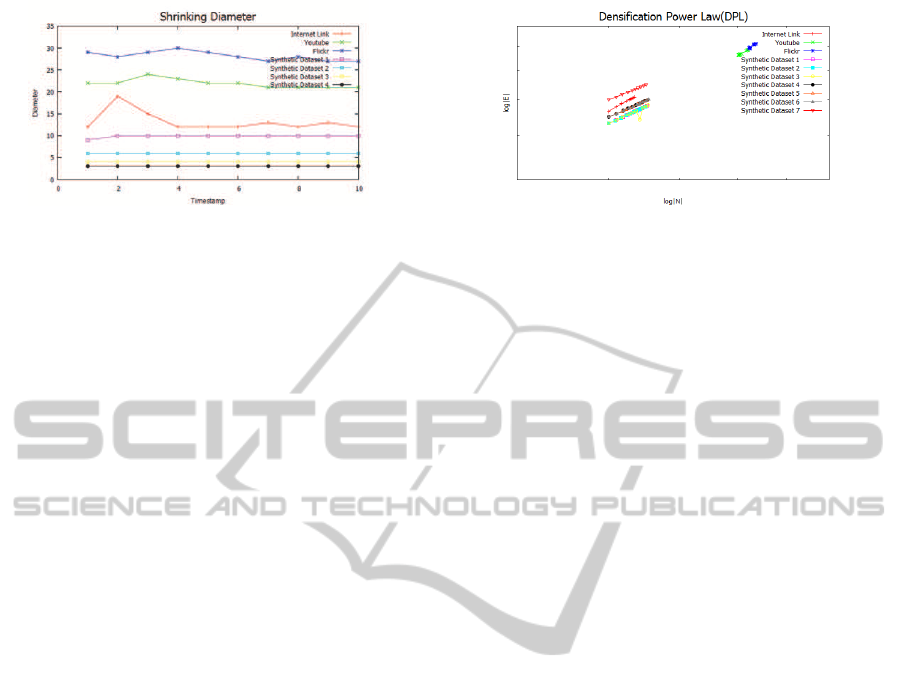
Figure 2: Shrinking Diameter.

4.3 Results of Dynamic Properties

Shrinking Diameter. Figure 2 shows plots of the

change in diameter values of the datasets over time

with timestamp value on x axis and diameter value

on y axis. The results of real graphs conform the

shrinking diameter property. In synthetic graphs, we

obtained stabilized diameter results over time, some

times even after a small increase. This is because of

the nature of the generator model which has prefer-

ential attachment property where the diameter grows

slowly with the number of nodes n.

Densiﬁcation Power Law (DPL). Our DPL results

are shown in Figure 3. All our real and synthetic

graphs obey the DPL, with exponents ranging be-

tween 1.06 and 1.24. The power-law exponent being

greater than 1 shows that there is a superlinearity be-

tween the number of nodes and the number of edges

in the graph.

5 CONCLUSIONS

In this paper, we presented a study on realistic so-

cial graph generation using Barabasi-Albert model.

We used static and dynamic graph properties to ana-

lyze synthetically generated graphs and measure how

ﬁt the generated graphs to the real one. We gen-

erated graphs with different parameter settings and

compared them to the real graphs.

Results indicate that greater preferential attach-

ment power value cause small diameter and radius

values with disrupting the power law degree distri-

bution of the graphs. The parameter of the number

of edges to add in each step effects the number of

edges in each timestamp and results in greater den-

siﬁcation power law degree. Synthetically generated

graphs do not obey shrinking diameter property of

dynamic social networks. However, they have bet-

ter clustering coefﬁcient degree with smaller diameter

than real graphs. Furthermore, these synthetic graphs

have power law degree distributions and ﬁt densiﬁca-

tion power law property of dynamic social networks.

Figure 3: Densiﬁcation Power Law.

ACKNOWLEDGEMENTS

The authors were supported by the Scientiﬁc

and Technological Research Council of Turkey

(TUBITAK) EEEAG project 110E027.

REFERENCES

Barabasi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks.

Chakrabarti, D. and Faloutsos, C. (2006). Graph min-

ing: Laws, generators, and algorithms. ACM Comput.

Surv., 38(1).

Erd¨os, P. and R´enyi, A. (1959). On random graphs i. Pub-

licationes Mathematicae Debrecen, 6:290.

Leskovec, J., Chakrabarti, D., Kleinberg, J. M., and Falout-

sos, C. (2005a). Realistic, mathematically tractable

graph generation and evolution, using kronecker mul-

tiplication. In Jorge, A., Torgo, L., Brazdil, P., Cama-

cho, R., and Gama, J., editors, PKDD, volume 3721 of

Lecture Notes in Computer Science, pages 133–145.

Springer.

Leskovec, J. and Faloutsos, C. (2007). Scalable modeling

of real graphs using kronecker multiplication. In Pro-

ceedings of the 24th international conference on Ma-

chine learning, ICML ’07, pages 497–504, New York,

NY, USA. ACM.

Leskovec, J., Kleinberg, J., and Faloutsos, C. (2005b).

Graphs over time: densiﬁcation laws, shrinking diam-

eters and possible explanations. In Proceedings of the

eleventh ACM SIGKDD international conference on

Knowledge discovery in data mining, KDD ’05, pages

177–187, New York, NY, USA. ACM.

Mislove, A. (2009). Online Social Networks: Measurement,

Analysis, and Applications to Distributed Information

Systems. PhD thesis, Rice University, Department of

Computer Science.

Mislove, A., Koppula, H. S., Gummadi, K. P., Druschel,

P., and Bhattacharjee, B. (2008). Growth of the ﬂickr

social network. In Proceedings of the 1st ACM SIG-

COMM Workshop on Social Networks (WOSN’08).

Travers, J. and Milgram, S. (1969). An Experimental Study

of the Small World Problem. Sociometry, 32(4):425–

443.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ’small-world’ networks. Nature, 393(6684):440–

442.

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

526