
F T E: A Fuzzy Timed Action Language
Youzhi Zhang, Xudong Luo
∗
and Yuping Shen
Institute of Logic and Cognition, Sun Yat-sen University, Guangzhou, 510275, China
Keywords:
Knowledge Representation, Action, Reasoning, Fuzzy Logic.
Abstract:
This paper proposes a fuzzy approach for reasoning about action and change in timed domains. In our method,
actions and world states are modeled as fuzzy sets over time axis. Thus, their temporal relations and time
constraints can be model as fuzzy rules. So, our method handles well the issue that action happens at an
approximate time and then the states change also at an approximate time, which has not been solved well in
existing work. Finally, our method is used to solve the classic problem of rail road crossing control in a fuzzy
environment. The theoretic and simulation analysis shows that the controller using our method works well.
1 INTRODUCTION
The study of Reasoning about Action and Change
(RAC) (Thielscher, 2011; Varzinczak, 2010; Mueller,
2009; Reiter, 2001; Shanahan, 1997; Sandewall,
1994) has been an active topic since the early days
of Artificial Intelligence (van Harmelen et al., 2008).
The main concern of RAC is to describe the evolu-
tion of a possible world by formalising actions and
their effects in timed domains (Shen et al., 2010),
which means that actions are required to be performed
within a certain amount of time or after a certain
amount of time that has elapsed.
However, few systems of RAC are developed for
the use in fuzzy environments. Nevertheless, the real
world is often fuzzy (Zadeh, 1965; Luo et al., 2002;
Luo et al., 2007; Huang et al., 2012). For example, an
action can be taken only at an approximate time or the
state is not very clear at an accurate time point. So,
it is necessary to extend these RAC systems to ones
that can be used in fuzzy environments. On the other
hand, Zadeh proposed fuzzy set theory (Zadeh, 1965),
which composes a form of many-valued logic (Zadeh,
1975; Luo et al., 2002). In fuzzy theory, reasoning
is approximate rather than crisp and fuzzy logic vari-
ables have a truth degree that ranges in-between 0
and 1 rather than 0 or 1 only. So, fuzzy theory is a
powerful tool for us to develop a method for fuzzy
RAC in timed domains. Thus, based on the work
of (Shen et al., 2010; Wan, et al. 2012), this paper
employs fuzzy set theory to develop a reasoning lan-
guage about fuzzy actions and fuzzy states over time.
The rest of the paper is organized as follows. Sec-
tion 2 reviews some necessary points in fuzzy theory.
∗
Corresponding author.
Section 3 presents our fuzzy timed action language.
Section 4 discusses how to use fuzzy logic to im-
plement fuzzy temporal relation in our timed action
language. Section 5 shows how to use our method
to solve the problem of rail road crossing control in
fuzzy environments. Section 6 discusses the related
work to show how our work advance the state-of-art
in the field. Section 7 concludes our work and points
out the future work.
2 PRELIMINARIES
This section will review some basics of fuzzy set the-
ory (Nanda and Das, 2010; Zadeh, 1965), which are
necessary for our system.
Definition 1. A fuzzy set, denoted as A, on domain U
is characterized by a membership function µ
A
: U 7→
[0, 1], and ∀u ∈ U, µ
A
(u) is called the membership
degree of u in fuzzy set A.
The following definition is about the implication
of the Mamdani method (Nanda and Das, 2010):
Definition 2. Let A
i
be a Boolean combination of
fuzzy sets A
i1
, ··· , A
im
, where A
i j
is a fuzzy set de-
fined on U
i j
, (i = 1, ··· , n; j = 1, · · · , m), and B
i
be
fuzzy set on U
0
, (i = 1, · · · , n). Then when the input is
µ
A
i1
(u
i1
), ··· , µ
A
im
(u
im
), the output of such fuzzy rule
A
i
→ B
i
is fuzzy set B
0
i
, which is defined as: ∀u
0
∈U
0
,
µ
i
(u
0
)=min{f (µ
A
i1
(u
i1
), ··· , µ
A
im
(u
im
)), µ
B
i
(u
0
)},
(1)
where f is obtained through replacing A
i j
in A
i
by
µ
i j
(u
i j
) and replacing “and”, “or”, “not” in A
i
by
“min”, “max”, “1 − µ”, respectively. And the out-
put of all rules A
1
→ B
1
, ··· , A
n
→ B
n
, is fuzzy set M,
295
Zhang Y., Luo X. and Shen Y..
F T E: A Fuzzy Timed Action Language.
DOI: 10.5220/0004258402950302
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 295-302
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

which is defined as: ∀u
0
∈ U
0
,
µ
M
(u
0
) = max{µ
1
(u
0
), ··· , µ
n
(u
0
)}. (2)
By Definition 2, the result what we get is still a
fuzzy set. To defuzzify the fuzzy set, we have follow-
ing centroid method (Nanda and Das, 2010):
Definition 3. The centroid point u
cen
of fuzzy set M
given by formula (2) is:
u
cen
=
n
∑
j=1
u
j
µ
M
(u
j
)
n
∑
j=1
µ
M
(u
j
)
. (3)
Actually, u
cen
in above is the centroid of the area,
that is formed by the curve of membership function
µ
M
and its horizontal ordinate.
3 FUZZY TIMED ACTION
LANGUAGE
This section will propose our fuzzy timed action lan-
guage.
3.1 The Syntax
Definition 4. A fuzzy timed action language, de-
noted as F T E , is a tuple hN, ∆, Φ, Θ, B(Θ)i, where
N is the set of natural numbers called time points, ∆ is
a non-empty set of action symbols representing fuzzy
actions at some approximate time points, Φ is a non-
empty set of state symbols representing fuzzy states,
Θ is a non-empty set of clock variables over N, B(Θ)
is the set of all clock constraints over Θ, each clock
constraint ψ ∈ B(Θ) is an expression of the form x
n or x − y n, where x, y ∈ Θ, ∈ {≤, <, =, >, ≥}
and n ∈ N.
The various forms of propositions in F T E are de-
fined as follows:
Definition 5. Giving a fuzzy timed action language
hN, ∆, Φ, Θ, B(Θ)i, let A ∈ ∆ represent a fuzzy action
over time axis, F ∈ Φ represent a fuzzy state over time
axis, λ ⊆ Θ be a set of clocks, C be a set of fuzzy states,
Ψ ⊆ B(Θ) be a set of clock constraints, and T ∈ N.
Then:
1. A fuzzy C-proposition is in the form of
A initiates F resets λ if C when Ψ. (4)
2. A fuzzy H-proposition is in the form of
A happens-at about T. (5)
3. A fuzzy O-proposition is in the form of
F holds-at about T. (6)
A domain description or theory in F T E is a finite
set of fuzzy C-propositions, fuzzy H-propositions, and
fuzzy O-propositions.
The fuzzy C-proposition means that if clock con-
straint Ψ and state precondition C are met, then fuzzy
action A happens, and causes fuzzy state F holds and
the set of clocks λ are reset. The fuzzy H-proposition
describes that fuzzy action A happens at about time
point T . Similarly, the fuzzy O-proposition describes
that fuzzy state F holds at about time point T .
3.2 The Semantics
Definition 6. For a fuzzy timed action language of
hN, ∆, Φ,Θ,B(Θ)i:
• A clock interpretation is a mapping of ν : Θ 7→
N. We say that ν satisfies a clock constraint of ψ,
written as ν |=
c
ψ, if ψ holds under ν according to
the standard arithmetic semantics. If there exists
such a ν, then ψ is satisfiable and ν is a solution
to ψ. For the set of clock constraints Ψ, ν |=
c
Ψ if
∀ψ ∈ Ψ, ν |=
c
ψ.
• A clock operation is that given δ ∈ N, ν + δ is
the clock interpretation that maps every x ∈ Θ to
ν(x) + δ; and for λ ⊆ Θ, ν[λ := 0] is the clock
interpretation that maps each x ∈ λ to 0 and every
clock y ∈ Θ\λ remains unchanged. In particular,
ν
0
is a clock interpretation that maps every clock
to 0.
For example, let Θ = {λ
0
}, then ν(λ
0
) = 2 satisfies
clock constraint 1 < λ
0
< 3. And ν + 3 = ν(λ
0
) + 3 =
5, meaning that the time of the clock λ
0
representing
is 5 now.
Definition 7. The interpretation of fuzzy O-
proposition (6) is a membership function given as
follows:
µ(t) =
0 if t > (T + r
2
),t < (T − r
1
),
1
r
1
(t − T ) + 1 if (T − r
1
) ≤ t ≤ T ,
1
r
2
(T − t)+ 1 if T < t ≤ (T + r
2
),
(7)
where µ(t) ∈ [0, 1] represents that fuzzy state F holds
to the degree of µ(t) at the time point of t, and r
1
and
r
2
represent the fuzzy ranges. Fuzzy H-proposition
(5) can be similarly interpreted as formula (7).
Definition 8. The interpretation of fuzzy C-
proposition (4) is as the following fuzzy rule:
((C ∧Ψ) ∧ A) → (F ∧ν[λ := 0]) (8)
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
296

By the Mamdani method (see Definition 2), from
(8) we can have:
((C ∧Ψ) ∧ A) ∧ (F ∧ ν[λ := 0]) (9)
Then, we can define the fuzzy action and fuzzy
state interpretation as follows:
Definition 9. The interpretation of fuzzy action A
and fuzzy state F is a mapping µ
AF
: N 7→ [0, 1],
where µ
AF
(t) means that fuzzy action A happens or
fuzzy state F holds at t to the degree of µ
AF
(t) where
(T − r
1
) ≤ t ≤ (T + r
2
), T is the time point in the H-
proposition or O-proposition, and r
1
and r
2
represent
the fuzzy ranges.
Definition 10. A fuzzy interpretation of an F T E
theory is defined as a pair of hµ
AF
, νi, where µ
AF
is a
fuzzy action and fuzzy state interpretation and ν is a
clock interpretation.
Definition 11. Let D be an F T E theory, hµ
AF
, νi
be an interpretation of F T E and F ∈ Φ, time point
T ∈ N and (T − r
1
) ≤ t ≤ (T + r
2
), where r
1
and r
2
represent the fuzzy ranges. Let λ
0
be the clock with
respect to t, and ν(λ
0
) = t
0
. For the interpretation of
H-proposition and O-proposition (7) and the interpre-
tation of fuzzy action A and fuzzy state F:
1. If there exists a subinterval [t
1
,t
2
] ⊆ [T − r
1
, T ]
such that if t
0
> t and t ∈ [t
1
,t
2
] then µ
AF
(t
0
) >
µ
AF
(t)), ∀t
0
∈ [t
1
,t
2
], then the points in [t
1
,t
2
] are
called initiation points.
2. If there exists a subinterval [t
1
,t
2
] ⊆ [T, T + r
2
]
such that if t
0
> t and t ∈ [t
1
,t
2
] then µ
AF
(t
0
) <
µ
AF
(t), ∀t
0
∈ [t
1
,t
2
], then the points in [t
1
,t
2
] are
called termination points.
Actually, formula (7) in the interpretation of H-
proposition and O-proposition usually has the in-
creasing part and the decreasing part. The initia-
tion points and the termination points represent the
increasing part and the decreasing part, respectively.
Furthermore, if the set of λ in C-proposition is
non-empty, then t is called a resetting point for λ in
hµ
AF
, νi with respect to D.
Definition 12. Let D be an F T E theory. Let λ
0
be
the clock with respect to t, and ν(λ
0
) = t
0
. Then the
interpretation of hµ
AF
, νi is called a model for D if
∀F ∈ Φ, A ∈ ∆, T ∈ N, and t ∈ [t
1
,t
2
] ⊆ [T − r
1
, T +
r
2
] (where r
1
and r
2
represent the fuzzy ranges), the
following conditions hold:
1. For each fuzzy O-proposition in D in the form of
“F holds-at about T ”, µ
AF
: N 7→ [0, 1], where
µ
AF
(t) means that fuzzy state F at t holds to the
degree of µ
AF
(t).
2. For each fuzzy H-proposition in D in the form of
“A happens-at about T ”, µ
AF
: N 7→ [0, 1], where
µ
AF
(t) means that fuzzy action A at t happens to
the degree of µ
AF
(t).
3. If there are no initiation points or termination
points in [t
1
,t
2
], ∀t
0
∈ [t
1
,t
2
], if t
0
> t, then
µ
AF
(t
0
) = µ
f
(t).
4. If the time points in interval [t
1
,t
2
] are initia-
tion points, ∀t
0
∈ [t
1
,t
2
], if t
0
> t, then µ
AF
(t
0
) =
max{µ
AF
(t), µ
AF
(t
0
)}.
5. If the time points in interval [t
1
,t
2
] are termina-
tion points, ∀t
0
∈ [t
1
,t
2
], if t
0
> t, then µ
AF
(t
0
) =
min{µ
AF
(t), µ
AF
(t
0
)}.
6. If t is not a resetting point in [t
1
,t
2
] for clock λ
0
,
∀t
0
∈ [t
1
,t
2
], if t
0
> t, then ν(t
0
) = ν(t) + (t
0
−t).
7. If t is resetting point in [t
1
,t
2
] for clock λ
0
, and
there exists no other resetting points in [t,t
0
], then
ν(t
0
) = ν[λ
0
:= 0] + (t
0
−t).
8. if the fuzzy C-proposition holds at t, then there
exists some corresponding µ
AF
> 0 and ν(t) |=
c
Ψ.
4 FUZZY MODELING
This section will explain our fuzzy modeling of action
and change in timed domains.
Proposition 1. In the F T E theory, the fuzzy action
can change the fuzzy state over time and in the time
constraints through fuzzy C-proposition.
In Proposition 1, the relation of the fuzzy action
and the fuzzy state is represented by the fuzzy C-
proposition. Now the further relation on the time axis
can be shown as following proposition:
Proposition 2. In the F T E theory, for the fuzzy ac-
tion and the same agent’s corresponding fuzzy state
that it causes, the fuzzy action can be represented by
the corresponding fuzzy state on the time axis.
Although a fuzzy action can be represented by the
corresponding fuzzy state on the time axis, if different
C-propositions are with respect to different agents, the
preconditions about states and time constraints still
need to be considered.
Proposition 3. In the F T E theory, the resetting time
points and the time constraints can be represented by
the time axis.
Thus, when all of variables are put on the time
axis, the resetting time points and the time constraints
do not need to be considered by Proposition 3. Now
we transform the fuzzy C-proposition to a simplified
fuzzy rule on the time axis.
FTE:AFuzzyTimedActionLanguage
297

Proposition 4. In the F T E theory, the fuzzy C-
proposition on the time axis can be modeled as:
F If C (10)
By Proposition 4, we can change fuzzy C-
proposition (8) as the following fuzzy rule:
C → F (11)
Further, by the Mamdani method (see Definition 2),
we have:
C ∧ F (12)
Then the fuzzy C-proposition are transformed to
the relation of the initiate states and the final state on
the time axis, which is easier to be handled. Then we
can use Mamdani method (2) and centroid method (3)
to defuzzify fuzzy sets C and F. The input is fuzzy set
C, and the output is fuzzy state set F. Thus, we can
see the clear change of F with C.
5 SCENARIO OF RAIL ROAD
CROSSING CONTROL
This section shows how to use our fuzzy approach to
solve the classical scenario of rail road crossing con-
trol (Alur, 1999) in a fuzzy environment with the help
of Matlab’s Fuzzy Inference System.
5.1 Fuzzy Modeling of Rail Road
Crossing Control
In the problem of rail road crossing control, there are
three agents: Train, Controller and Gate. At a state,
the train can send a signal to the controller, then the
controller must send the corresponding signal to the
gate within 1 minute, and finally the gate must close
or open within 1 minute. In particular, the train should
send the corresponding signal to the controller at least
2 minutes before it enters the crossing and it must exit
after it enters the crossing within 3 minutes.
The train’s possible actions are Approach, En-
ter and Exit, and its states are Far-approaching, Ap-
proaching, Close-approaching, Close-exit, Exit and
Far-exit.
• Far-approaching means that the train is approach-
ing but it is a little far from the crossing.
• Approaching means that it is between Far-
approaching and Close-approaching.
• Close-approaching means that the train is ap-
proaching (i.e., very close to the crossing).
Figure 1: The train’s speed membership functions.
Figure 2: The train’s states membership functions.
The train’s states Close-exit, Exit and Far-exit have
the similar meaning. And Inside-gate means that the
train is in the gate.
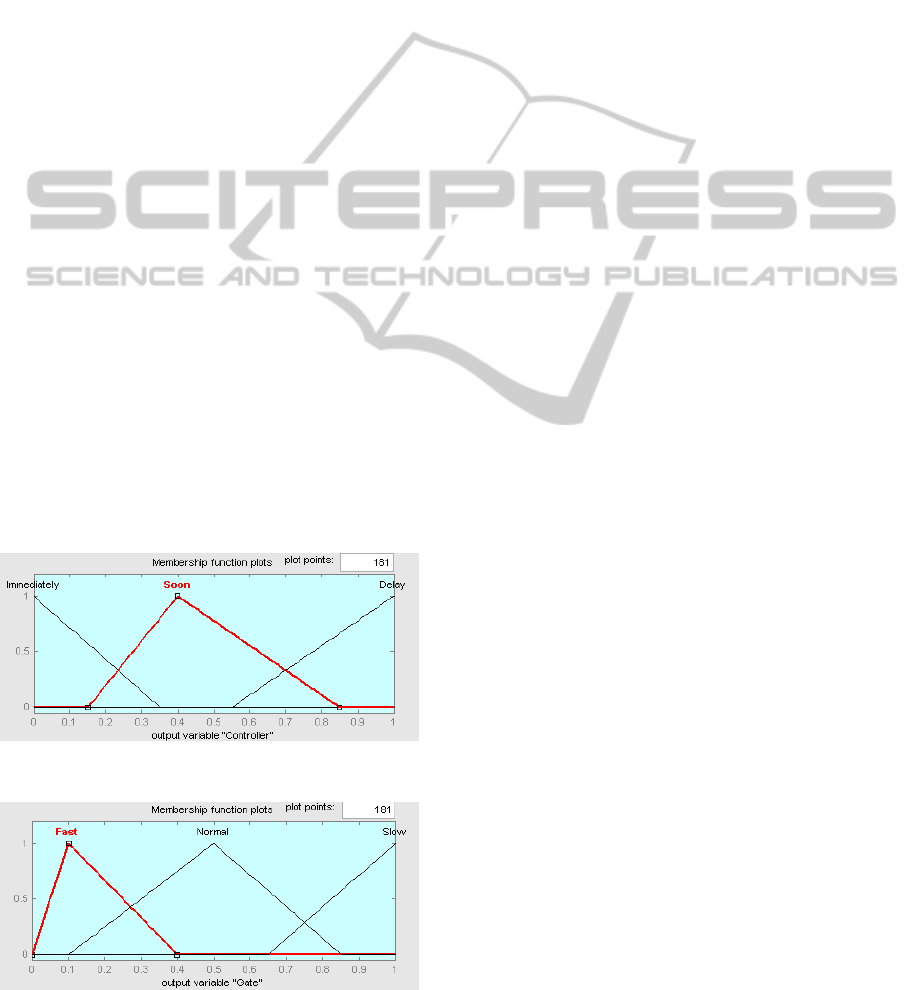
The controller has three states, which describe
how long to wait for sending the signal to the gate
after it receives a train signal. These states are Imme-
diately, Soon, and Delay. Similarly, the gate also has
three states, which describe how fast to close or open
the gate. These states are Fast, Normal, and Slow.
We assume that the signals of Far-approaching, Ap-
proaching, Close-approaching, and Inside-gate make
the gate closed and the signals of Close-exit, Exit, and
Far-exit make the gate open. The controller can take
one action (i.e., Send), and the gate can take two ac-
tions (i.e., Close and Open).
In the real world, we should consider the speed of
the train. Actually, when the train is approaching, the
higher the train’s speed, the faster the train gets closer
to the crossing, and so the faster the controller and
the gate needs to take actions for safety and saving
time for passerbies. Therefore, different train’s speeds
need to be put into account. Thus, we add the speed of
the train as an input variable, which values are Slow,
Fast, and Veryfast and their membership functions are
as shown in Figure 1.
Let λ
1
be the clock for the train, λ
2
be the clock
for the controller, and λ
3
be the clock for the gate.
Suppose we can have two fuzzy H-propositions in the
form of formula (5) as follows:
Send happens-at about T (13)
Close happens-at about T
0
(14)
where T ∈ N is the time point at about which the con-
troller sends a signal, and T
0
∈ N is the time point
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
298
at about which the gate is closed. And we can have
two fuzzy C-propositions in the form of formula (4)
as follows:
if Slow and Far-approaching when 0.55 ≤ t
then Send initiates Delay resets λ
3
, (15)
if Slow and Far-approaching when 0.65 ≤ t
0
Close initiates Slow. (16)
where (T −r
1
) ≤ t ≤ (T + r
2
) and (T
0
− r
0
1
) ≤ t
0
≤
(T
0
+r
0
2
) (r
1
, r
2
, r
0
1
, and r
0
2
represent the fuzzy ranges).
By Proposition 1, we can have two fuzzy O-
propositions in the form of formula (6) as follows:
Delay holds-at about T (17)
Slow holds-at about T
0
(18)
where T ∈ N is the time point at about which the con-
troller’s state delay holds, and T
0
∈ N is the time point
at about which the gate’s state Slow holds. Similarly,
we describe other states in this way.
By Propositions 2 and 3, we can represent fuzzy
actions by fuzzy states, and put the clock and clock
constraints on the time axis. Then, we can operate
them in the Matlab’s Fuzzy Inference System. If we
set that the time of 2 minutes before the train enters
the crossing is the time of zero, then the train must exit
at the time of 5 as shown in Figure 2. The controller
and the gate must do something within 1 minute and
so we represent this by two output variables as shown
in Figures 3 and 4. We have one input variable as de-
scribing the states of the train. The train states’ mem-
bership functions as shown in Figure 2.
Figure 3: The controller’s membership functions.
Figure 4: The gate’s membership functions.
Now we use the membership functions (see Fig-
ures 3 and 4) to describe our two output variables. By
Proposition 4, we can model C-propositions (15) and
(16) as follows:
Delay if Slow and Far-approaching, (19)
Slow if Slow and Far-approaching. (20)
Now we consider the rules between the inputs and
outputs. The main rules are that when the train is
approaching, the higher speed and the closer to the
crossing the train, the faster the controller and the gate
take actions for safety and saving time for passerbies.
From rules (19) and (20), we can get our first rule:
Delay and Slow if Slow and Far-approaching. (21)
That is:
1. If (TrainSpeed is Slow) and (TrainState is Far-
approaching) Then (Controller is Delay) and
(Gate is Slow).
Similarly, we can get other rules in the problem and
put them into Matlab’s Fuzzy Inference System.
5.2 Analysis of the Fuzzy Model in
Safety and Effectiveness
By using formula (3) to the fuzzy set of formula (12),
we can get all the rules’ result of defuzzification. Now
we can see the output of the fuzzy reasoning by Sur-
face Viewer of Matlab as shown in Figures 5 and 6.
For example, when the train speed is 100 km per hour
and the time is 0, the controller should send the sig-
nal to the gate in 0.354 minute and the gate should be
closed in 0.388 minute. Actually, Figure 5 shows how
the controller changes with the train speeds and the
train states; and Figure 6 shows how the gate changes
with the train speeds and the train states.
For a rail road crossing control system, it should
satisfy the criteria of safety and effectiveness. That
is, to be safe, the gate should be closed as soon as
possible when the train is approaching, and the gate
should be open gently when the train is leaving; to
be effective, (i.e., in order to save time for passer-
bies), the gate should not be closed too early when the
train is approaching, and the gate should be opened
for passerbies as soon as possible when the train left
far away. In our system, the gate is controlled by the
controller according to the gate’s states. Figures 5 and
6 show that our system satisfies the criteria of safety
and effectiveness. We have assumed that the train en-
ters the gate at about the time point of 2. So, when the
time is close to the left of the time point of 2 (i.e., the
train approaches very closely to the gate), it is danger-
ous for passerbies and so the controller and the gate
FTE:AFuzzyTimedActionLanguage
299

Figure 5: Controller’s states change with inputs.
Figure 6: Gate’s states change with inputs.
should take some measures as quickly as possible.
When the time is far from the left of the time of 2, the
controller should delay some time for passerbies, and
the gate need close gently for being safer. However,
when the time point is close to the right of the time
point of 2, which means that the train is leaving but
it is still close to the gate, or the tail of the train may
be still on the crossing. Thus, the controller should
delay some time to send the signal, and the gate can
close gently for safety. When the train is leaving, and
far from the gate (i.e., far from the right of time point
of 2), it is safe for passerbies, and thus the controller
and the gate should take some measures as quickly as
possible to save the time for passerbies.
Figs. 7(a) and (b) illustrate that how the con-
troller and the gate synchronize with the train’s states
at a specific train’s speed. The curves decrease first,
then do not change when it reaches the curve bottom,
which means that the train is approaching to the gate
and the controller and the gate all should take actions
as quickly as possible. Then the curve increase sud-
denly, which means that the train is leaving, but it is
still closed to the gate, and so the controller and the
gate need not to do the things quickly. Then the curve
is going down just as the discussion above.
Figs. 7(c) and (d) illustrate how the controller
and the gate synchronize with the train’s speeds when
we have a specific train’s state at the time point of 0.
From both two figures, we know that when the train’s
speed is higher, then the controller and the gate both
should take the measures as soon as possible. Actu-
ally, we know that if anything wrong, the train needs
to stop. The faster the train, the more time the train
(a) (b)
(c) (d)
Figure 7: (a) and (b): The controller’s state and the gate’s
state change with the train’s states when the train’s speed is
100 km/h; (c) and (d): The controller’s state and the gate’s
state change with the train’s speeds at the time point of 0.
needs to stop. So, our system can ensure this situation
safe.
From above illustration, we can have some prop-
erties for our system as follows:
Theorem 1. In the rail road crossing control sys-
tem, for any different train speeds, if the train sends
the corresponding signal at least 2 minutes before the
train enters the crossing, meaning that the time point
is at the left of zero point, the gate can be closed when
the train enters the crossing.
Theorem 2. In the rail road crossing control system,
for any different train speeds, the gate can be open
within 2 minutes after the train sends the correspond-
ing signal to the controller when the train is leaving.
Theorem 1 shows that our system is safe, and the
Theorem 2 shows that our system is effective. From
the above analysis, we can conclude that our system
satisfies the criteria of safety and effectiveness.
6 RELATED WORK
Fuzzy reasoning about action and change in timed do-
mains is related to fuzzy automata theory, fuzzy finite
state machine, fuzzy timed transition system, fuzzy
representation and control. In the following, we will
check them one by one.
Firstly, we examine the research about fuzzy au-
tomata theory. In (Tiwari et al., 2012), fuzzy automata
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
300

theory based on a lattice-ordered monoid is proposed
and the associated topology is studied. They intro-
duce the separatedness and connectedness properties
of these fuzzy automata. In (Li, 2011), proposed are
the lattice-valued finite automata, which generalize
the fuzzy automata with membership values in a dis-
tributive lattice. In (Stamenkovi
´
c and Ciri
´
c, 2012), an
effective method for constructing an equivalent fuzzy
finite automaton from a given fuzzy regular expres-
sion is provided. However, all of these fuzzy automata
only consider the states only (do not consider fuzzy
action over time), while our work considers states and
actions both.
Secondly, we discuss the research about fuzzy fi-
nite state machine. In (G
´
omez et al., 2011), G
´
omez
et al. propose a fuzzy finite state machine and
a fuzzy transformation semigroup with the interval
truth structure of the transition function. In (Alvarez-
Alvarez et al., 2011), fuzzy finite state machines
are used for body posture recognition. In (Alvarez-
Alvarez et al., 2012), an automatic method based on
fuzzy finite state machines and genetic algorithms are
used to model the human gait. In these fuzzy finite
state machines, states and time have been considered,
but they do not consider the fuzzy time constraints
and how fuzzy actions change the states. Rather, we
do.
Thirdly, we check the research about timed tran-
sition. Our model of fuzzy action and state reason-
ing can be actually viewed as a fuzzy timed transition
system because the transitions are based on approxi-
mate time. In (Andr
´
es et al., 2011), a novel approach
is presented to self-adaptive systems by a fuzzy-time
formal model, whose main concepts are clocks and
clock constrains. The system can reflect the behav-
ior of fuzzy timed systems, but unlike us, they do not
model how the actions change the states. In (Cao et
al., 2011), a fuzzy transition system, which deals with
how the actions change states, is used to measure the
behavioral similarity of states. However, they did not
concern fuzzy time constraints, while ours does not
have the problem. In (Acampora et al., 2010), a timed
fuzzy controller is developed to manage the temporal
component by pairing the initial location of a timed
automaton with a fuzzy controller, representing the
system’s initial control configuration, and associating
each automaton transition with a collection of oper-
ators. This system can maximize performances and
robustness. Although this system has applied to many
real situations and it has considered time constraints
and states’ change, it does not consider actions and
how actions change the states, while we do in this pa-
per.
Fourthly, we have a look at the research on fuzzy
representation and control. In (Schiffe, 2011), the
method of fuzzy action representations and control for
robot is proposed by extending the action language,
which is developed for the high-level control of agents
and robots. However, this fuzzy representation does
not consider fuzzy time and time constraints, and so
it cannot handle the problem that our method can. In
(Schiffer, 2012), the fuzzy action representation is im-
proved by a thorough integration of qualitative repre-
sentations and reasoning for positional information,
but they still do not handle fuzzy time and time con-
straints. In (Barbosa et al., 2010), a new way of fuzzy
reasoning is proposed by combining the feature of
fuzzy controllers with the feature of fractional con-
troller of PID-type. It makes the controllers better
at superior robustness and wider domain of applica-
tion. However, in real world, we cannot neglect that
actions change states under time constraints. How-
ever this mixed controller fails to incorporate them,
while we do. In (Ribaric and Hrkac, 2012), a model
of fuzzy spatio-temporal knowledge representation is
proposed. Nevertheless, unlike our method in this pa-
per, it cannot deal with that the fuzzy actions change
states based on constraints of state and time.
7 SUMMARY
In this paper, we propose a fuzzy approach for reason-
ing about action and change in timed domains. In our
method, actions, states and time constraints are repre-
sented by fuzzy sets over time axis and the temporal
rules are modeled by fuzzy rules. This is significant
because when the actions change the states flowing
the time flash and in the time constraints, all of these
often happen in the fuzzy environment of real life. So,
fuzzy reasoning about action and change in timed do-
mains is more realistic in the real world, and thus we
can use it in many real situations. To illustrate this,
we use our approach to solve the problem of classic
rail road crossing control in a fuzzy environment and
analyse the problem with the help of Matlab. More-
over, our simulation and theoretical analysis show our
treatment on the problem is safe, effective and effi-
cient. In the future, we will consider more complex
situations to improve our system and put it into prac-
tice.
ACKNOWLEDGEMENTS
This paper is supported by Bairen plan of Sun Yat-sen
University, China; National Natural Science Foun-
FTE:AFuzzyTimedActionLanguage
301

dation of China (No. 61173019); major projects of
the Ministry of Education, China (No. 10JZD0006);
and Young Scholar Research Projects of Guang-
dong Province, China (Nos. GD10YZX03 and
WYM10114).
REFERENCES
Acampora, G., Loia, V., Vitiello, A. (2010): Hybridiz-
ing Fuzzy Control and Timed Automata for Model-
ing Variable Structure Fuzzy Systems. Proceedings of
2010 IEEE International Conference on Fuzzy Sys-
tems, 1-8
Alur, R. (1999): Timed Automata. Proceedings of the 11th
International Conference on Computer-Aided Verifi-
cation. Lecture Notes in Computer Science, 1633, 8-
22
Alvarez-Alvarez, A., Gracian Trivino, G., Cord
`
on, O.
(2011): Body Posture Recognition by Means of a
Genetic Fuzzy Finite State Machine. Proceedings of
the 5th IEEE International Workshop on Genetic and
Evolutionary Fuzzy Systems, 60-65
Alvarez-Alvarez, A., Trivino, G., Cord
´
on, O. (2012): Hu-
man Gait Modeling Using a Genetic Fuzzy Finite
State Machine. Proceedings of 2012 IEEE Transac-
tions on Fuzzy Systems, 20(2), 205-223
Andr
´
es, C., Llana, L., N
´
u
˜
nez, M. (2011): Self-Adaptive
Fuzzy-Timed Systems. Proceedings of 2011 IEEE
Congress on Evolutionary Computation, 115-122
Barbosa, R. S., Jesus, I. S., Silva, M.F. (2010): Fuzzy Rea-
soning in Fractional-Order PD Controllers. In: New
Aspects of Applied Informatics, Biomedical Electron-
ics & Informatics and Communications, 252-257
Cao, Y., Wang, H., Sun, S. X., Chen, G. (2011): A Be-
havioral Distance for Fuzzy-Transition Systems. The
Computing Research Repository: abs/1110.0248v1
G
´
omez, M., Lizasoain, I., Moreno, C. (2012): Lattice-
Valued Finite State Machines and Lattice-Valued
Transformation Semigroups. Fuzzy Sets and Systems,
(In Press)
Huang, Z., Huang, Q. (2012): To Reach Consensus Us-
ing Uninorm Aggregation Operator: A Gossip-Based
Protocol. International Journal of Intelligent Systems,
27(4), 375-359
Li, Y. (2011): Finite Automata Theory with Member-
ship Values in Lattices. Information Sciences, 181(5),
1003-1017
Luo, X., Zhang, C., Jennings, N. R. (2002): A Hybrid
Model for Sharing Information Between Fuzzy, Un-
certain and Default Reasoning Models in Multi-Agent
Systems. International Journal of Uncertainty, Fuzzi-
ness and Knowledge-Based Systems, 10(4), 401-450
Luo, X., Jennings, N. R. (2007): A Spectrum of Compro-
mise Aggregation Operators for Multi-attribute Deci-
sion Making, 171(2-3), 161-184
Mueller, E. T. (2009): Automating Commonsense Reason-
ing Using the Event Calculus. Communications of the
ACM, 52(1), 113-117
Nanda, S., Das, N. R. (2010): Fuzzy Mathematical Con-
cepts. Alpha Science Intl Ltd
Reiter, R. (2001): Knowledge in Action: Logical Foun-
dations for Specifying and Implementing Dynamical
Systems. MIT Press
Ribaric, S., Hrkac, T. (2012): A Model of Fuzzy Spatio-
Temporal Knowledge Representation and Reasoning
Based on High-level Petri Nets. Information Systems,
37(3), 238-256
Sandewall, E. (1994): Features and Fluents: The Represen-
tation of Knowledge about Dynamical Systems, vol.
1, Oxford University Press, Oxford
Schiffer, S., Ferrein, A., Lakemeyer, G. (2011): Fuzzy Rep-
resentations and Control for Domestic Service Robots
in Golog. Intelligent Robotics and Applications, Lec-
ture Notes in Computer Science, 7102, 241-250
Schiffer, S., Ferrein,A., Lakemeyer, G. (2012): Reasoning
with Qualitative Positional Information for Domestic
Domains in the Situation Calculus. Journal of Intelli-
gent & Robotic Systems, 66(1-2), 273-300
Shanahan, M. (1997): Solving the Frame Problem: A Math-
Ematical Investigation of the Common Sense Law of
Inertia. MIT Press
Shen, Y., Dang, G., Zhao, X. (2010): Reasoning about
Action and Change in Timed Domains. Proceedings
of the 13th International Workshop on Nonmonotonic
Reasoning, Toronto, Canada
Stamenkovi
´
c, A., Ciri
´
c, M. (2012): Construction of Fuzzy
Automata from Fuzzy Regularexpressions. Fuzzy Sets
and Systems, 199, 1-27
Thielscher, M. (2011): A Unifying Action Calculus. Artifi-
cial Intelligence, 175(1), 120-141
Tiwari, S. P., Singh, A. K., Sharan, S. (2012): Fuzzy Au-
tomata Based on Lattice-Ordered Monoid and Asso-
ciated Topology. Journal of Uncertain Systems, 6(1),
51-55
van Harmelen, F., Lifschitz, V., Porter, B. (2008): Hand-
book of Knowledge Representation. Elsevier Science
Varzinczak, I. (2010): On Action Theory Change. Journal
of Artificial Intelligence Research, 37, 189-246
Wan, H., Ma, Y., Xiao, X., and Shen, Y (2012): τε2asp
: Implementing T E via Answer Set Programming.
PRICAI 2012: Trends in Artificial Intelligence, Lec-
ture Notes in Artificial Intelligence, 7458, 820-825
Zadeh, L. A. (1965): Fuzzy Sets. Information and Control,
8(3), 338-353
Zadeh, L. A. (1975): Fuzzy Logic and Approximate Rea-
soning, Synthese, 30(3-4), 407-428
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
302
