
Numerical Kernels for Monitoring and Repairing Plans Involving
Continuous and Consumable Resources
Enrico Scala
Dipartimento di Informatica, Universita’ di Torino, Via Pessinetto 117, Turin, Italy
Keywords:
Planning, On-line Planning, Repair, Monitoring, Plan Execution, Reactive AI.
Abstract:
In this paper we introduce a technique for monitoring and repairing a plan dealing with continuous and con-
sumable resources. The mechanism relies on the notion of numerical kernel. Concretely, a numerical kernel
establishes the sufficient and necessary conditions for a plan to be valid in a specific state of the system. We
employ the mechanism in a continual planning agent and we evaluate experimentally the approach for the
Zenotravel domain. Results show good cpu-time w.r.t. a traditional replanning from scratch.
1 INTRODUCTION
In the last decade of research in AI, an increas-
ing amount of work has been devoted in extending
the automated planning (and especially the classi-
cal paradigm) in dealing with real world problems
((Hoffmann, 2003), (Gerevini et al., 2008)). One of
the most limitations in the classical setting is the lack
in the management of consumable and continuous re-
sources. In this perspective, the concept of numeric
planning has been introduced (Fox and Long, 2003).
However, while many efforts have been success-
fully devoted for the problem of off-line plan genera-
tion, just a little amount of work has been addressed
in studying the plan of actions for the on-line phase,
making exception for the works dealing with the tem-
poral dimension. In this context models as STP (Sim-
ple Temporal Problem) and DTP (Disjunctive Tem-
poral Problem) have been extensively adopted and
some extensions have been proposed ((Conrad and
Williams, 2011), (Policella et al., 2009), (Stergiou
and Koubarakis, 2000)).
The main contribution of this paper is a technique
for monitoring and repairing a plan involving contin-
uous and consumable resources modeled as numeric
state variables. The technique grounds on the notion
of numerical kernel, which is a set of inequality con-
ditions allowing to directly (without performing any
search and any propagation) assess the sufficient and
necessary requirements that must be guaranteed in a
particular state of the system to be consistent with the
plan at hand. To demonstrate the utility of the tech-
nique, we propose a continual planning agent which
is able to deal with unexpected resource consump-
tion. To validate our approach, we experimented the
mechanism in two versions of the Zenotravel domain,
namely a well known test-bed developed by the plan-
ning community as a benchmark for testing the per-
formance of planners.
2 BACKGROUND
In the following we introduce the planning framework
our approach applies
1
. The following definitions ex-
tend the traditional STRIPS formalism analogously
to numeric expressions reported in (Fox and Long,
2003).Moreover, since the plan is the main object of
study for the monitoring and repair problem, we will
consider fully instantiated actions, as a plan typically
involve specific instances of actions instead of their
schema.
System State. To model resources our state of the
system extends the classical formulation with a vec-
tor of real values N which maps each resource in a
continuous value. Moreover, also other numeric con-
tinuous information can be modeled (e.g. the distance
among two sites).
Model of Actions. Since continuous resources can
be consumed and required by actions, the classical
STRIPS setting is not sufficient. To this end, tran-
sitions in our system are represented by means of nu-
meric action. That is:
1
We assume the reader is familiar to the planning for-
malism.
531
Scala E..
Numerical Kernels for Monitoring and Repairing Plans Involving Continuous and Consumable Resources.
DOI: 10.5220/0004260205310534
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 531-534
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Definition 1 (Numeric Action). A numeric action is
a STRIPS action in which propositional preconditions
and effects are augmented with:
• numeric precondition, which is a conjunction of
comparisons, where each comparison is an in-
equality of the form { exp {<,≤,=,≥,>} exp’}.
• numeric effects, which consists of a set of opera-
tions, where each operation is defined by means
of { f,{+ =,− =,=},exp}, and f is the resource
affected by the operation, i.e. f ∈ N
In the definition above exp,exp
′
are arith-
metic expressions involving a variety of resources
and numeric information from N. Informally,
the numeric operations model how a numeric ac-
tion affects the resources (e.g., power = power +
distance(A,B)/avg consumption), while the numeric
precondition expresses the resource requirements for
the action applicability (e.g., power > 5.0). The nu-
meric action is applicable in a state S if both the nu-
meric and classical preconditions are satisfied in S.
The application of this action in a state S will trans-
form S in S
′
according to (i) the operations defined in
the numeric effects, and (ii) the traditional add/delete
list reported in the propositional effects.
The Plan. By focusing on the numeric part of the
state we can define a numeric plan as follows:
Definition 2 (Numeric Plan). A numeric plan is a to-
tal ordered set of numeric actions that, starting from a
state I, leads the agent in a state satisfying a goal G,
where: (i) I is a numeric state, i.e., a vector assign-
ing values to the numeric information of the domain,
(ii) G is the numerical goal for the agent containing
a conjunction of comparisons as the ones defined for
the action preconditions.
3 MONITORING AND REPAIR
VIA NUMERICAL KERNEL
While the planning phase generally assumes deter-
ministic state transitions, the execution of the plan in
the real world can be prevented because of the pres-
ence of exogenous events as well as unexpected ac-
tion behaviors. Therefore a continuous monitoring is
often desirable for understanding if the observations
(i.e. the state) are consistent with the plan at hand.
In this context, the only checking of action pre-
conditions may, in general, does not suffice. Albeit
the action can result applicable, the executability of
the rest part of the plan could depend by only certain
resources profiles. To capture such profiles, it is im-
portant to keep trace to the conditions expressed in the
goals and the model of actions present in the plan.
3.1 Numerical Kernel
Given a numeric plan π as the one in Definition 2, it
is possible to find the set of conditions that must be
guaranteed for achieving G by means of π. We will
this set numerical kernel. More formally, from (Scala,
2012):
Definition 3 (Numerical Kernel). Given a plan π, a
goal G and a state S, a set of comparisons K over N
is said to be a numerical kernel for π and G when the
state S[π] satisfies G iff S satisfies K.
where S[π] is the state obtained from the recursive ex-
ecution of π starting from S. Thus, given a state of the
system, by verifying the condition expressed in the
numerical kernel, one can infer if the state is compat-
ible with the remaining plan for reaching the goal.
More precisely it is possible to find a numerical
kernel for each step of the plan by backward propaga-
tion starting from G. That is,
the computation starts with the last numerical ker-
nel as it corresponds to the (trivial) numerical kernel
for an empty plan, i.e. the goal conditions. After
which, the remaining part of the kernels is constructed
by combining the information involved in the model
of the action (pre(a) and eff(a)) with the (previously
computed) next numerical kernel. In particular it is
necessary to iteratively combine the set of compar-
isons with the set of assignments listed in the opera-
tions set. Note indeed that every operation listed in
the model of the action can be transformed in an as-
signment operation. The procedure and the notion of
numerical kernels are introduced and described in de-
tail in (Scala, 2012).
Triangle table defined in (Fikes et al., 1972) have
been introduced for a similar motivations by introduc-
ing the concept of propositional kernel. However, the
formulation of a kernel expresses precisely what is the
minimal set of propositionalatoms that must hold dur-
ing the plan execution. Here, the numerical kernel ex-
presses just the boundary of a state space to be valid
without specifying a particular state.
3.2 Monitoring and Repairing
To validate and motivate the utility of numerical ker-
nels, we developed a continual planning agent which
is in charge of dealing with continuousresources. The
continual planning paradigm (desJardins et al., 1999)
allows the agent to interleave the execution and the
planning for the purpose of repairing its plan of ac-
tions once unexpected conditions (in our case the ker-
nel violation) occur. Hence the usage of numerical
kernel is rather appropriate as the agent performs both
monitoring and repair, throughout the plan execution.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
532

In order to handle plans involving both proposi-
tional and numerical aspects, we combined the notion
of the numerical kernel defined in this paper with the
propositional kernels defined for classical planning.
Algorithm 1: Monitoring and Repair.
Input: P: plan of numerical actions G: goal
Output: Success or Failure
K = KernelsComputation(plan,G)
i = 0
while plan is not empty do
SenseAndUpdate(S)
if S satisfies K[i] then
action = head-remove(plan)
execute(action)
i++
else
patch = repair(S,K[i])
if patch != null then
plan = plan.concat(patch)
else
plan = replan(S,G)
K = KernelsComputation(plan,G)
i=0
SenseAndUpdate(S)
if S satisfies G then
return Success
else
return Failure
The algorithm above reports the strategy of the
agent. It is quite similar to the main algorithm for the
continual planning reported in (Brenner and Nebel,
2009), making exception that here the agent has to
deal with continuous resources. For this reason, this
strategy includes an explicit way of repair, and a more
focused way to perform the monitoring.
The algorithm starts by computing the proposi-
tional and numerical kernel; then it retrieves the ker-
nel for this part of the plan and compares the condi-
tions against the current observed state of the system.
If both conditions are verified, namely the proposi-
tional and the numerical kernel, it extracts and exe-
cutes the next action from the plan; otherwise it looks
for a plan towards a state in which both propositional
kernel and numerical kernels are satisfied. The idea is
to re-establish the necessary conditions for the appli-
cation of the rest part of the plan.
Since the approach is not complete as the repair
mechanism is not allowed to search over all the search
space (the one generated from the current state to-
wards the goal), the agent can switch to replanning
from scratch when the patch via repair is not found.
As a common continual planning approach the algo-
rithm terminates once the plan is finished and the goal
reached. The strategy supports the most of the level
of expressiveness of PDDL 2.1 level 2, with the lim-
itation that propositional and numeric preconditions
must be conjunctively separated.
4 EXPERIMENTAL RESULTS
To verify the feasibility of the repair mechanism pre-
sented in the previous Section, we applied the strat-
egy to the ZenoTravel domain, which is a domain in-
troduced by the planning community for the Interna-
tional Planning Competition (IPC3
2
).
To make this domain more challenging, we pro-
posed an extended version in which refuel is possible
only in certain city. To obtain this we modified the
refuel action precondition for allowing its execution
only in city in which it is explictly stated the pres-
ence of the refuel station. This means that a plane has
to carefully choose the paths for moving persons all
around. We performed experiments in both domains,
that will be called the normal and hard domain.
Starting from the suite of numeric problems gen-
erated for the competition and for the purpose of vali-
dating our approach, we injected discrepancies on the
way in which the fuel is consumed. We focus on the
7 most difficult cases where we injected 5 different
amounts of noise, which consequently has produced
different instances of repair problems. The total num-
ber of experiments is 35 cases for each domain. For
each case we measured the performance of the ap-
proach in terms of cpu-time spent
3
.
Figure 1 and 2 summarize the results for two dif-
ferent strategies. The one (line with rhombuses) is
the repair strategy (we turned off the replanning from
scratch), the other one (line with squares) is the re-
planning from scratch methodology (we turned off the
repair mechanism). Both strategies have been experi-
mented for the normal and the hard domain.
More precisely, the figures measure the computa-
tional effort for solving the impasse. In case of re-
pair, the solution corresponds to the bridge towards
the kernel, whereas for the replanning from scratch
the obtained new plan links the current state directly
with the goal. The x-axis enumerates the 7 cases con-
sidered whereas the y-axis the computational effort.
It is quite clear that for this class of problems, the
repair mechanism outperforms the replanning from
scratch in all cases we tested, and it is true even when
dealing with hard cases. In this latter cases the re-
planning performs rather bad since the performance
degrades rapidly. For instance in cases number 6 the
2
http://planning.cis.strath.ac.uk/competition/
3
Tests ran on an Intel Core Duo (1.66 Ghz) with 2 GB
of Ram. The implementation is in Java 1.6 and the planner
used is metric-ff (Hoffmann, 2003)
NumericalKernelsforMonitoringandRepairingPlansInvolvingContinuousandConsumableResources
533
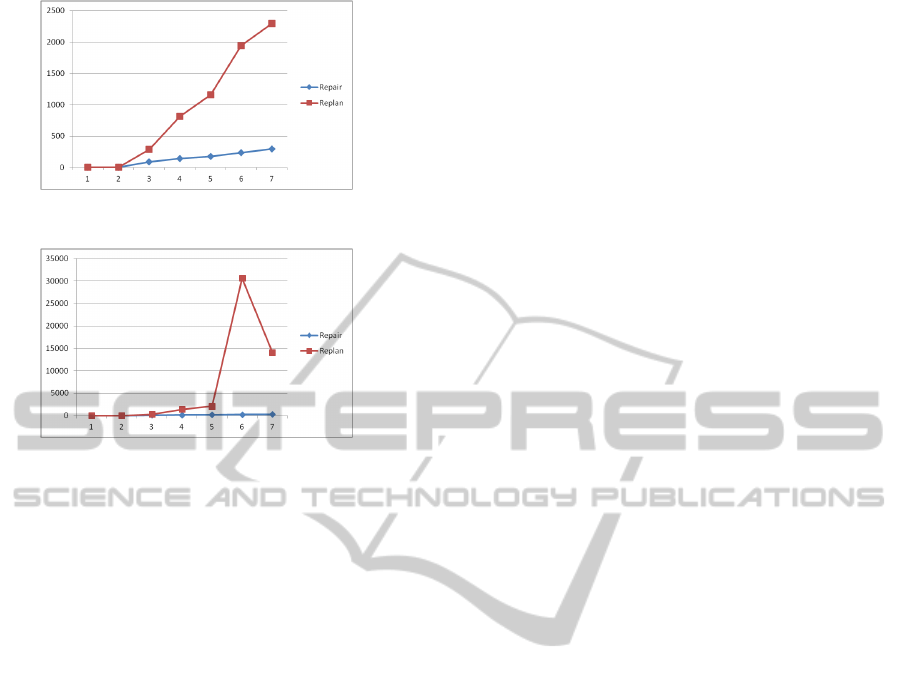
Figure 1: ZenoTravel Domain (Normal); Cpu time.
Figure 2: ZenoTravel Domain (Hard); Cpu time.
replanning from scratch found a solution only after 30
seconds of cpu-time.
5 CONCLUSIONS
The paper proposes a new technique for monitoring
and repairing plans with actions dealing with contin-
uous and consumable resources. The technique ex-
ploits the notion of numerical kernel developed in
(Scala, 2012) accompanied to the well known propo-
sitional kernel. The strategy allows to focus the agent
just on a specific portion of the state which is the only
interesting for the monitoring and repair problem.
The repair via plan adaptation is a very attractive
area of research in AI since, despite opposite formal
complexity results (Nebel and Koehler, 1995), the re-
pair have been proved to be a viable solution in prac-
tice instead of a replanning from scratch. However
previous works have been largely applied just for the
classical paradigm (Gerevini and Serina, 2010).
For this reason, we applied the numerical kernel
notion for a repair problem via plan adaptation, and
we studied the performance of the system against a
blind replanning from scratch. Tests have been per-
formed on a well known benchmark domain defined
by the planning community. Results showed that,
when the repair has to face unexpected resources con-
sumption, a focused repair may work very well w.r.t. a
replanning mechanism. As an immediate future work
we would like to test the developed repair strategy
on a larger set of domains, to understand the gener-
ality of the repair approach. Moreover, we would like
to study a more sophisticated way in the selection of
the kernels towards which perform the patch; in this
first version in fact we employ a conservative setting
in which the repair is performed directly towards the
state that was expected. Moreover it would be inter-
esting to exploit the numerical kernel in the general
context of Case Based Planning.
REFERENCES
Brenner, M. and Nebel, B. (2009). Continual planning and
acting in dynamic multiagent environments. Jour-
nal of Autonomous Agents and Multiagent Systems,
19(3):297–331.
Conrad, P. R. and Williams, B. C. (2011). Drake: An effi-
cient executive for temporal plans with choice. Jour-
nal of Artificial Intelligence Research, 42:607–659.
desJardins, M. E., Durfee, E. H., Ortiz, C. L., and Wolver-
ton, M. J. (1999). A Survey of Research in Dis-
tributed, Continual Planning. AI Magazine, 20(4).
Fikes, R., Hart, P. E., and Nilsson, N. J. (1972). Learning
and executing generalized robot plans. Artificial Intel-
ligence, 3(1-3):251–288.
Fox, M. and Long, D. (2003). Pddl2.1: An extension to pddl
for expressing temporal planning domains. Journal of
Artificial Intelligence Research, 20:61–124.
Gerevini, A. and Serina, I. (2010). Efficient plan adapta-
tion through replanning windows and heuristic goals.
Fundamenta Informaticae, 102(3-4):287–323.
Gerevini, A. E., Saetti, A., and Serina, I. (2008). An ap-
proach to efficient planning with numerical fluents
and multi-criteria plan quality. Artificial Intelligence,
172(8-9):899–944.
Hoffmann, J. (2003). The metric-ff planning system: Trans-
lating ”ignoring delete lists” to numeric state vari-
ables. Journal of Artificial Intelligence Research,
20:291–341.
Nebel, B. and Koehler, J. (1995). Plan reuse versus plan
generation: A theoretical and empirical analysis. Ar-
tificial Intelligence, 76(1-2):427–454.
Policella, N., Cesta, A., Oddi, A., and Smith, S. (2009).
Solve-and-robustify. Journal of Scheduling, 12:299–
314.
Scala, E. (2012). Numerical kernel for plans dealing
dealing with continous and consumable resources.
Technical Report available at http://www.di.unito.it/
∼scala/kerneltr.ps.
Stergiou, K. and Koubarakis, M. (2000). Backtracking al-
gorithms for disjunctions of temporal constraints. Ar-
tificial Intelligence, 120(1):81–117.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
534
