Real-time Information Querying over Peer-to-Peer Networks using

Timestamps

Michael Gibson and Wamberto Vasconcelos

Department of Computing Science, University of Aberdeen, Aberdeen, U.K.

Keywords:

Agents, Peer-to-Peer, Information Propagation, Real-time.

Abstract:

Most P2P networks are used for ﬁle-sharing applications. These forms of applications mainly rely on key-

word searching to locate ﬁle resources on the peers. Whilst this querying is suitable for many data-intensive

applications, it is not suitable for applications where data changes over short periods of time, also known as

time-critical applications. We investigate the use of timestamps on a peer’s knowledge about an application to

create queries so that other peers may reply with more up-to-date information to keep the peer’s knowledge

up-to-date. We propose means to synchronise peers to provide them with a shared, independent clock so that

they utilize timestamps. To show that a peer’s knowledge about a time-critical application affects the perfor-

mance of other peers, we carried out experiments to show information propagation over a P2P network and

use various metrics to evaluate our approach.

1 INTRODUCTION

Information propagation is the distribution of in-

formation between peers and is one of the major

challenges in (pure) peer-to-peer (P2P) networks be-

cause there are no servers to direct messages among

the peers. Therefore protocols have been devel-

oped to help facilitate this. Most of these proto-

cols are suitable for data-intensive applications be-

cause of their ability to locate resources through the

use of keywords. These protocols include ﬂooded

request and document routing (Taylor and Harrison,

2008) which have been used in commercial applica-

tions, such as Gnutella (Taylor and Harrison, 2008).

While keyword-searching allows peers to retrieve re-

sources themselves, the disadvantage of this is the

peers are acting “selﬁshly”—they will not voluntarily

contribute resources to assist other peers. Wu (2009)

looks into how faster peers share their bandwidth with

slower peers so that all peers complete the download

of resources at the same time.

This research focus on real-time applications

where it is important that each peer has a shared

view of the global information. Instead of peers shar-

ing ﬁles with each other, they will share information

about a common, but independent, application with

each other to keep each peer’s perception of the appli-

cation up-to-date. To evaluate the performance of the

application over P2P networks, the applications them-

selves must reﬂect the performance of each peer in

terms of how their knowledge of the application will

affect other peers. Therefore, we will use computer

games as the domain. Computer games have differ-

ent types of data-intensive and time-critical properties

and the performance of a game is dependent on the

abilities of each player (peer) within the game. How-

ever this does not mean our proposed solution is lim-

ited to one domain. The games will be encoded as

rules—when certain conditions are met, then an ac-

tion takes place. The purpose of this is two-fold: the

information requirements of the rule can be checked

to make sure the rule is legal to ﬁre, if not then the

peer will have to perform other actions (most likely

query other peers) to make the rule legal and most do-

mains can be encoded as a set of rules. Our proposed

solution is thus impartial to any rule-based domain.

Although we mainly mention peers, this is a syn-

onym for agents. Generally speaking, a peer is only

responsible for handling messages to and from oth-

ers whereas agents can make decision for themselves

within their environment as well as communicate with

other agents. Although our primary focus is on P2P

research, when dealing with applications, agents are

required to evaluate the current situation of the ap-

plication as well as neighbouring peers to make de-

cisions on how to continue executing the application.

This is especially important when running automated

tasks like our experiment in Section 4. Therefore,

282

Gibson M. and Vasconcelos W..

Real-time Information Querying over Peer-to-Peer Networks using Timestamps.

DOI: 10.5220/0004261102820287

In Proceedings of the 5th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2013), pages 282-287

ISBN: 978-989-8565-38-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

when we mention peer, we don’t necessarily mean

just the messaging handled by a generic peer, but

the inclusive body of the application, agent and peer

working together to handle application execution, de-

cision making and message handling.

To further explain the proposed research, this doc-

ument has been laid out in the following sections;

Section 2 covers related work in sharing knowledge

over P2P networks; Section 3 looks into our proposed

solution in how peers join a network and contribute

information to other peers; Section 4 describes our

experiment to show how knowledge accuracy affects

the performance of peers; Section 5 looks into how we

evaluated our experiment and its results and Section 6

concludes the document with how our current evalua-

tion turned out with regards to our proposed solution

and what we aim to accomplish in the future.

2 RELATED WORK

Since our chosen domain is computer games, we will

cover existing work regarding games on P2P net-

works and how it differs from our work. Neumann

(2007) provides a survey regarding the issues related

to gaming and P2P, namely game-state management.

Most games use the client/server architecture because

the server acts as the manager for all events and states

within a game. Without this manager, players would

not be able to know the current status of the game en-

vironment. Current frameworks tackle this with the

use of interest management (Bharambe et al., 2008;

Fan et al., 2007) which works by making players be

only interested in other players depending on their

virtual distance. For example, if two players are in-

teracting in the game, then they are both interested in

sharing data with each other since they will see the

results of the other player’s actions. Other techniques

similar to interest management; for example, zoning

(partitioning a game world for close players to com-

municate within) has also been looked at with the use

of frameworks (Glinka et al., 2007). The biggest is-

sue with these kinds of frameworks is they are only

useful for computer games and not for other domains.

Although we are using games as our domain, they will

only be used for testing our solutions and the solutions

themselves will be adaptable to any domain.

For our research, we need up-to-date results so

that each peer will have accurate knowledge for opti-

mal contribution to the network. One of the common

themes between interest management work and our

research is the use of database-related queries (Cas-

tano et al., 2003; Nejdl et al., 2002) to retrieve data be-

tween peers. Whilst this is useful for updating a peer’s

own knowledge, there is no time limit on sending and

receiving knowledge, just as long as the knowledge

will eventually contribute to the community of peers.

This is not suitable for us because time-critical appli-

cation require information as soon as possible in order

to be useful. Liu (2011) uses polymorphic queries to

attempt to retrieve attributes from other peers if the

queried peer does not contain all of the requested at-

tributes. However, because this uses an algorithm to

forward queries to other peers depending on its “qual-

ity”, the queries will only be approximately answered

and we need accurate answers.

Ensuring that each peer is synchronised with each

other requires a form of distributed timekeeping. It

is unreasonable to assume all distributed systems will

run at the same speed and have the exact same time as

each other so a relative approach is required. Lam-

port logical clocks (Lamport, 1978) allows events

among distributed systems to be ordered between

themselves. This is especially important for dis-

tributed information systems because the order of re-

ceived messages will have an effect on the output –

rearranging the order of events will typically produce

different outcomes. Lamport clocks uses timestamps

from sent and received messages to resynchronise its

clock so that future messages from other sources will

not arrive out-of-order. Another way to keep dis-

tributed systems synchronised is to use a common

clock so that all systems will have the same time

as each other, leading to accurate global timestamps.

The Network Time Protocol (NTP) (Mills, 2003) uses

servers with accurate clocks to provide systems with

the current time. However, there are disadvantages

in using NTP for synchronization: depending on the

server the time may not be fully accurate and the time

it takes for the time message to arrive at the requestor

will affect the real time; this is even more so for dis-

tant requestors to the same server.

3 PROPOSED SOLUTION

In our solution, two major algorithms are used dur-

ing a peer’s lifetime in an application: bootstrapping

and query generation and sending. This document

only provides an overview of the algorithms used in

our solution, but detailed explanations can be found

in Gibson et al. (2012).

Bootstrapping only occurs once in a peer’s life-

time to join a network, but query generation and send-

ing occurs at every application (game) cycle. Other

parts of a peer’s lifetime have been omitted as these

occur during the application cycle.

One main disadvantage of P2P networks is the

Real-timeInformationQueryingoverPeer-to-PeerNetworksusingTimestamps

283

Algorithm 1: Bootstrap.

Input : S = haddress, porti, speed

Output: P = {p

, p

,..., p

}, N

= {n

,...,n

speed

1 connect(S)

2 send(S,speed)

3 receive*(S,hspeed

,remainingTime, P,Ni)

4 for n ∈ N do

5 send(n,PING) // Gnutella PING-PONG

6 end

7 while remainingTime > 0 do

8 receive(A,msg)

9 let msg be of the form htype,in f oi

10 if type = PONG then

11 N

← N

∪ {A} // Gnutella PING-PONG

12 else if type = SPEED then

13 speed

← in f o

14 end

15 end

16 if |N

| > 0 then

17 startGame(P, speed

)

18 end

lack of an entry point for new peers to join an existing

network. Most existing P2P applications tackle this

using an entry-point node, typically called a “boot-

strapping node” so that new peers can either directly

join the bootstrapping node and form neighbourhoods

from it, or download a list of peer addresses to di-

rectly connect to. The latter method is commonly

used in BitTorrent with the use of a tracker and in

Gnutella with the use of web caches (Taylor and Har-

rison, 2008). Because of the ease of using a bootstrap-

ping node and a list of available peers, we have used

these methods in our solution. This allows new peers

to directly join a bootstrapping node which sends the

peer a list of available peers to directly connect to.

Algorithm 1 (A1) explains the bootstrapping pro-

cedure; how a peer joins a network. The inputs are

the bootstrapping node’s address and port, S, and the

peer’s game playing speed, speed. The outputs are

the peer’s player attributes, P, the peer’s list of con-

nected neighbours (as well as their player details), N

and the game speed to play at, speed

. P allows oth-

ers to identify this peer’s player within the game and

allowing this peer to update its own player attributes.

To generate queries to update a peer’s (B) knowl-

edge about the application, the knowledge has to be

explicit. So a reasoner is able to infer what needs

to be retrieved for B to continue participating. How

the knowledge is explicitly stored and managed de-

pends on the application domain. This applies to the

reasoner as well; how it creates queries to update B’s

knowledge depends on how the knowledge is handled.

For example, let’s say the domain was a car racing

game. Apart from knowing important information

Algorithm 2: Query Generation and Send.

Input : N = {n

,...,n

}, Q = {q

,...,q

R = {r

,...,r

}, S = {s

,...,s

T hreshold

Output: Q = {q

,...,q

}, S

= {s

,...,s

}

1 Q

←

2 S

← S

3 for s ∈ S do

4 let s be of the form hv,ti

5 if v /∈ Q and v /∈ Q

and t ≥ T hreshold then

6 Q

← Q

∪ {v}

7 S

← S

\ {s}

8 end

9 end

10 for v ∈ Q

11 send(bestNeighbour(v,N), request(v))

12 end

13 Q ← Q ∪ Q

about each players’ location and position, knowing

when this information was taken affects how each

player plays the game. Therefore, being able to show

the age of each piece of information allows the rea-

soner to generate update queries depending on how

old the information is, hence the use of timestamps.

Algorithm 2 (A2) explains how queries are created

based on the age of game variables. The inputs are

B’s set of connected neighbours (created from A1),

N, a set of previously queried variables, Q, the vari-

ables used to control each player in the game, S, and

a time limit to represent when a piece of information

becomes out of date, T hreshold. The outputs are an

updated set of queries to ask each player, Q, in order

to update B’s information about the queried player(s)

and an updated list of player variables to be used with

the game rules in the current game cycle, S

4 EXPERIMENT

To evaluate our proposed research, we have devised

an experiment to show how the accuracy of knowl-

edge affects the performance of a peer which will

have an affect on neighbouring peers. The test ap-

plication is a simple racing game where players have

to complete a certain number of laps around a circu-

lar track to win. To encourage competition, the play-

ers are able to use the shortest lane to complete a lap

sooner, travel at various speeds and are allowed to

overtake slower players. There are also penalties to

consider as well; each player has a limited amount of

fuel and is consumed quicker if the player is travel-

ling fast. A pit stop is available for refuelling, but it

is only available at one point along the track and re-

quires time to fully refuel a player. If the player runs

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

284

out of fuel before the pit stop, the player loses. Play-

ers can overtake or independently move to outside

lanes providing they do not crash into others. Whilst

outside lanes are useful for overtaking, they have a

longer length than inside lanes so it is not advanta-

geous to remain on the outside for long periods of

time. By forcing players to pick the best route whilst

being conservative with fuel, the game will be com-

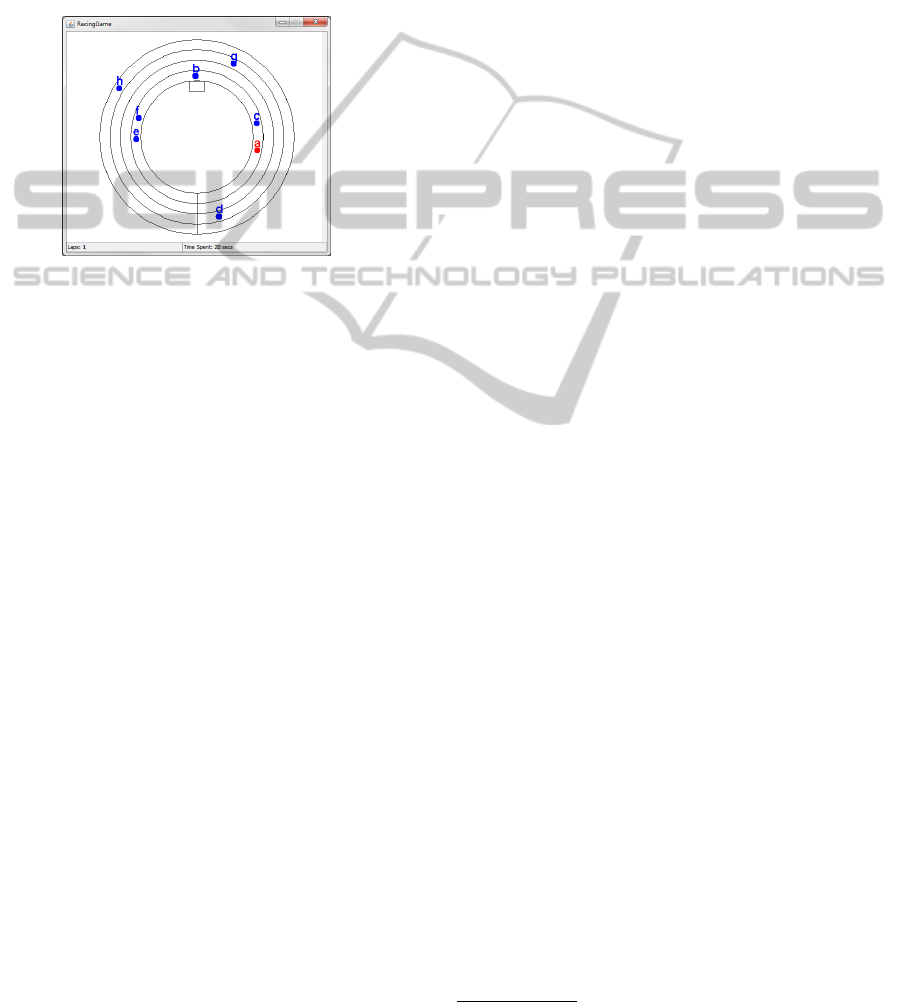
petitive, strategic and fun. Figure 1 shows player A

playing the racing game with seven opponents.

Figure 1: The racing game application running.

For our experiment, we have eight peers which

will run their own copy of the game and be able to

communicate with each other. Each peer will be able

to play the game as a player with the capacity to win

and play by the rules. The peers are based on the Rete

algorithm with rules to control where the peer may

move to depending on its condition and the locations

of the opponents. They also perform random moves,

such as change lanes and speed to simulate a human

player and to encourage the peers to perform more

update queries so that their knowledge base of oppo-

nents is kept up-to-date. For a simple racing game like

this, more than eight players may be too much for an

“enjoyable” experience, but the results will help us

reﬁne our proposed mechanism for larger-scale and

more data-intensive applications.

In each conﬁguration, each peer’s perception of

the game will have to be compared with the other

peers’ perceptions. This will allow us to use a con-

vergence metric to see how close an opponent’s per-

ception of a player state is in relation to the player’s

actual state. For the racing game, the most important

attributes to keep up-to-date are the player’s location

(in terms of lane and how far around the track) and

speed since these determine how an opponent will

react. There are also other attributes which are not

as important, but will affect how the game is played

as well; for example, the player’s fuel to see if they

require a pit stop and the number of laps to see if

they have won. By seeing if an opponent’s percep-

tion of a player’s attributes is accurate over time, as

well as vice versa, should lead to accurate gameplay

by both parties. However, since queries are only di-

rected to the closest virtual player, distant players may

not have constant accurate perceptions of each other.

This should not be a problem though because it is

unlikely they will interact with each other due to the

distance between themselves–this is related to interest

management. Since this will have an effect during the

comparison of perceptions, weights will have to be al-

located to show that the difference of player states be-

tween distant players is not as important as the differ-

ence of player states between close or neighbouring

players. As a game continues and players overtake

others, the importance of perceptions between play-

ers will constantly change but should lead to accurate

gameplay among each player’s closest opponent.

5 EVALUATION

For our evaluation we ran four experiments to show

how the “hops” of a message affects each peer’s per-

ception of its opponents. A hop refers to how many

peers a message will be sent to before the message is

classed as expired and therefore not to be forwarded

any more. A hop is commonly referred to as the time-

to-live (TTL) of a message. Since we are using eight

peers in a ring topology, each experiment sets each

message to hop one, two, three and four times respec-

tively. This ensure that at least one experiment (four

hops) will enable all peers to communicate with each

other with no dropped messages. Since a message

can travel in either direction from a peer, the furthest

distance to travel to reach all peers is four hops be-

cause of three intermittent peers in each direction, en-

suring that a message with four hops will reach any

peer within the 8-peer ring topology.

To enable ﬁne control over our experiments, we

have created our own in-house P2P simulator called

P2P Tool

which allows us to create peers with certain

rule sets and custom topologies around structured or

unstructured presets. It also allows us to manage how

messages are directed among peers and how peers

should deal with certain types of messages.

In order to show how affective our mechanism is,

we use the metric of divergence to show how differ-

ent a peer’s perceived knowledge of another peer dif-

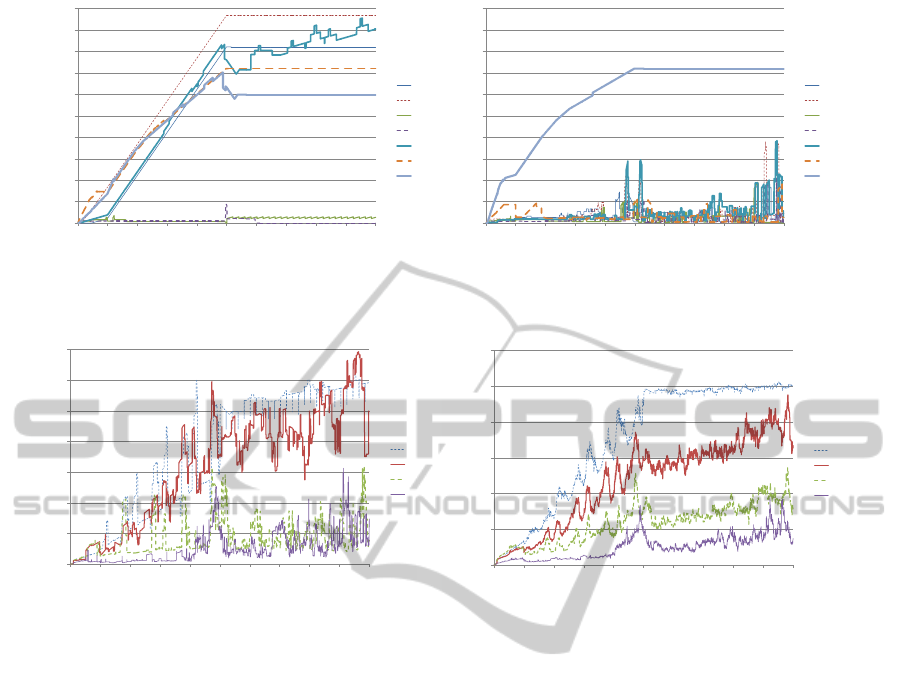
fers from the other peer’s actual knowledge. Figure

2 shows how much a peer (in this case, D) diverges

from opposing peers over game time. Whilst we only

show peer D’s perceptions of peers A, B, C, E, F, G

and H, every peer will produce similar looking graphs

https://github.com/msgibson/P2PTool

Real-timeInformationQueryingoverPeer-to-PeerNetworksusingTimestamps

285

due to each peer being equal with each other in terms

of relative neighbours and functionalities. In this doc-

ument, only the experiments with one and three hops

will be discussed; discussions on hops two and four

as well as how our mechanism differs from a pure ex-

haustive search are available in (Gibson et al., 2012).

To calculate the divergence of a peer, we calcu-

late the difference between the peer’s knowledge of

each opponent with the opponent’s actual knowledge

at each game tick. For each graph, the higher the di-

vergence, the more different the perceived and actual

values are, leading to inaccurate gameplay.

In Figure 2(a), each message only lasts one hop,

meaning only the immediate neighbours of D (peers

C and E) will receive messages. The graph shows that

peers C and E mostly have a low divergence, mean-

ing the perceived knowledge peer D has of C and E

are close to C and E’s actual knowledge respectively.

However for the remaining peers (A, B, F, G and H)

divergence is high because D is never able to commu-

nicate with them. Peers A, B, G and H appear to ﬂat-

line around the 5000 game tick point because in all in-

stances (peer D’s perception and the actual peers con-

trolling the players), the players seem to have “lost”

(ran out of fuel) at the same time. The divergence is

still high because the perceived and actual player po-

sitions will be at different locations around the track.

Figure 2(b) shows that since messages can arrive

at more distant peers, the divergence among these

peers will be smaller. For three hops, peers A and

G can be reached. Since peer H is never in reach, it

always has a high divergence. There are some spikes

in divergence in the reachable peers. We believe this

is caused when peer D tries to overtake the reachable

peers in its copy of the game, but failing to complete

the overtake. This may affect the peer’s closest oppo-

nents, leading to ﬂuctuating thresholds for the oppo-

nents and affecting queries being sent.

By looking at Figures 2(a) and 2(b), total diver-

gence among the peers decreases as the number of

hops increases. This should be obvious because as

messages are able to reach more peers, information

retrieved will be more accurate and hence lower di-

vergence. To show how much hop count improves

information accuracy, Figure 3 shows how peer D’s

convergence with all peers combined improves over

time with increasing hop count and how all peers ben-

eﬁt from increased hop count for their convergences.

In Figure 3(a), the graph shows that as the num-

ber of hops increases per message, the divergence is

generally lower at each point in game time. Each

line represents the average of each opponent percep-

tions from each experiment. For hops one and two

though, hop two’s divergence spikes over hop one’s

divergence at some points. This is also present in hops

three and four where hop three’s divergence spikes

over hop four’s divergence at some points. These

spikes are likely caused by the spikes seen in Figures

2(a) and 2(b), resulting in some errors being carried

over. To smooth out the errors, we averaged each

peer’s total divergences (each peer’s version of the

graph in Figure 3(a)) and applied weighting to the

closest players of each peer at each game tick to high-

light divergences in the closest opponents are more

important than divergences in distant players since

closer opponents are in the player’s interest set. This

combination of peer divergences and weightings led

to Figure 3(b) which clearly shows that as hop count

increases for messages, all peers improve because of

lower divergence, leading to more accurate applica-

tion performance and gameplay.

6 CONCLUSIONS, DISCUSSION

AND FUTURE WORK

In this paper, we have discussed an alternative ap-

proach to exchanging information over P2P networks

through the use of timestamps. We have also showed

how we approach this using rule-based applications

(speciﬁcally, but not limited to, computer games) by

evaluating the age of its knowledge base and gener-

ating queries to a peer who will be able to update

the information. Finally, we showed and explained

our experiment results to show how our approach per-

forms in varying conﬁgurations. Using the experi-

ment results will allow us to further reﬁne our pro-

posed approach for other types of applications, specif-

ically data-intensive applications.

Although the results may be obvious in showing

that as message hops increases, a peer’s perception of

other peers improves, it conﬁrms that our mechanism

of reducing queries based on certain times throughout

an application’s life leads to similar results compared

with an exhaustive querying to all peers.

We will use the results to develop our research to

focus on data-intensive applications as well as im-

prove our simulator’s performance to minimise di-

vergence spikes. This will mean looking at other

means of creating queries depending on the state of

the player instead of just time. One area that will

be focussed on more in the future is security. Whilst

running our experiment, we assume that all peers are

trustworthy and have no devious intentions. This is

not a reasonable approach for real-world applications

though. One area that should be focussed on is rogue

messages. Peers may be able to “lie” by sending

wrong information about itself or even other peers so

ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence

286

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Divergence

Game Tick

(a) 1 hop

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Divergence

Game Tick

(b) 3 hops

Figure 2: Peer D’s divergence with other peers over game time.

2000

4000

6000

8000

10000

12000

14000

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Divergence

Game Tick

Hops

(a) Peer D’s divergences over hops

2000

4000

6000

8000

10000

12000

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Divergence

Game Tick

Hops

(b) All peers’ divergences over hops

Figure 3: Comparison of divergences over hops.

that it can gain an advantage in a game. This can be

prevented by comparing the new received informa-

tion with a peer’s own information to see if there is

a signiﬁcant difference between them. If there is a

large difference, then it is likely the new information

is false so it should be discarded. The new informa-

tion could also be compared with neighbouring peers

to see if they think the information is false.

REFERENCES

Bharambe, A. et al. (2008). Donnybrook: Enabling Large-

Scale, High-Speed, Peer-to-Peer Games. SIGCOMM

Comput. Comm. Rev., 38:389–400.

Castano, S. et al. (2003). HELIOS: A General Framework

for Ontology-Based Knowledge Sharing and Evolution

in P2P Systems. In DEXA ’03.

Fan, L. et al. (2007). Mediator: A Design Framework for

P2P MMOGs. In Proc. of the 6th ACM SIGCOMM work-

shop on network and system support for games.

Gibson, M. et al. (2012). Towards Time-Critical Applica-

tions running on Peer-to-Peer Networks. Unpublished

manuscript. Available at http://db.tt/YRDSFoS1.

Glinka, F. et al. (2007). RTF: A Real-Time Framework

for Developing Scalable Multiplayer Online Games. In

Proc. 6th ACM SIGCOMM workshop on network and

system support for games, pages 81–86.

Lamport, L. (1978). Time, Clocks, and the Ordering

of Events in a Distributed System. Commun. ACM,

21(7):558–565.

Liu, J. and Fan, W. (2011). Polymorphic Queries for P2P

Systems. Inf. Syst., 36:825–842.

Mills, D. L. (2003). A Brief History of NTP Time: Memoirs

of an Internet Timekeeper. SIGCOMM Comput. Com-

mun. Rev., 33(2):9–21.

Nejdl, W. et al. (2002). EDUTELLA: A P2P Networking

Infrastructure Based on RDF. In Proc. of the 11th Int.

Conf. on World Wide Web.

Neumann, C. et al. (2007). Challenges in Peer-to-Peer

Gaming. SIGCOMM Comput. Comm. Rev., 37:79–82.

Taylor, I. and Harrison, A. (2008). From P2P and Grids to

Services on the Web. Springer.

Wu, C. et al. (2009). Time-Critical Data Dissemination in

Cooperative Peer-to-Peer Systems. Global Telecomms.

Conf., 2009. GLOBECOM 2009. IEEE, pages 1–6.

Real-timeInformationQueryingoverPeer-to-PeerNetworksusingTimestamps

287