
Efficient Self Adapting Agent Organizations
Kamilia Ahmadi and Vicki H. Allan
Computer Science Department, Utah State University, UT 84322-4205, Logan, U.S.A.
Keywords: Adaptation, Self-organization, Meta-Reasoning and Reorganization.
Abstract: Self-organizing multi-agent systems provide a suitable paradigm for agents to manage themselves. We
demonstrate a robust, decentralized approach for structural adaptation in explicitly modelled problem
solving agent organizations. Based on self-organization principles, our method enables the agents to modify
their structural relations to achieve a better completion rate of tasks in the environment. Reasoning on
adaptation is based only on the agent’s history of interactions. Agents use the history of tasks assigned to
their neighbours and completion rate as a measure of evaluation. This evaluation suggests the most suitable
agents for reorganization (Meta-Reasoning). Our Selective-Adaptation has four different approaches of
Meta-Reasoning, which are 1) Fixed Approach, 2) Need-Based Approach, 3) Performance-Based Approach,
and 4) Satisfaction-based Approach along with a Reorganization approach, which needs less data but makes
better decisions.
1 INTRODUCTION
A multi-agent system consists of interacting
intelligent agents and their environment. Agents can
be software agents, robots, or humans. Multi-agent
systems solve problems that are difficult or
impossible for an individual agent to solve alone. In
multi-agent systems, interaction between agents is
one of the important factors, which allows them to
find each other and exchange information.
Social interaction and success in jointly solving
problems determines a desirable structure for the
organization of agents. The task environment
contains a stream of tasks requiring some services,
and agents need to provide these services by
providing required resources. The number of links
and the specific connections are designed to
minimize communication overhead and facilitate
task completion.
Autonomous systems, capable of de-centralized
self-organization, have been proposed as a solution
for managing complex computing systems that must
deal with node failure and dynamic problem
characteristics. Responding to their own history of
interactions, individual agents exhibit the ability to
modify the organizational structure. Our adaptation
method is based on the agents forging and dissolving
relations with other agents. Agents use the history of
tasks assigned to their neighbours and the degree of
successful completion of these tasks as a measure of
evaluation. The system evaluates existing links for
possible increase or decrease in the overall
performance. After finding the target neighbours for
reorganization, the agent may decide to change the
two-way relationship with them or replace the target
agent with another agent for probable improvement.
Various approaches promote self-organization,
like reward-based mechanisms for selfish agents,
stigmergy (indirect coordination through the
environment), reinforcement mechanisms, and
cooperative actions of agents (Kota, 2008). Each of
these approaches has advantages and disadvantages,
but none of them directly deals with organization
structure. Self-organized systems are decentralized,
without any external control. Such autonomic
systems are more robust as there will not be a single
point of failure.
2 PREVIOUS WORK
Much research exists in self-adapting multi-agent
systems (Alberola, 2012, Dayong, 2012, Zheng-
guang, 2006). In (Barton, 2008), the network
structure is composed of agents (having a given skill
set) and connections between agents. Tasks
requiring a set of skills are introduced into the
system. Agents communicate with other agents
within n network links in their surrounding network.
This surrounding network is the agent’s local
294
Ahmadi K. and H. Allan V..
Efficient Self Adapting Agent Organizations.
DOI: 10.5220/0004261902940303
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 294-303
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
neighbourhood. A set of agents form a coalition to
complete each task. In this model, all completed
tasks have equal utility, while uncompleted tasks
have zero utility. Agents attempt to reorganize
themselves to improve the utility of the system.
Barton evaluates several approaches in this work.
The egalitarian approach chooses to establish
connections to agents, which have relatively few
connections. The inventory approach connects
agents possessing a needed skill in the
neighbourhood. The structural approach seeks to
connect to agents with the largest number of
connections. They examine the behaviours of
different mentioned methods (Barton, 2008). This
differs from our model in that a tree of SIs is not
considered, and the model permits only one kind of
relationship between agents.
In (Miralles, 2009), the authors structure the
problem as a set of resources which work together to
share data. A separate meta-level is in charge of
adaptation. A peer can potentially contact any other
agent, but typically, it interacts with a small number
of them. Agents reorganize in response to changes
in connection quality or information flow. Each
connection is limited in terms of number of units of
data that can be sent in a time step.
(Sansores, 2008) present a self-organization rule-
based approach is used to control the behaviour of
adapting agents, and reinforcement learning uses
memory of adaptations.
Kota et al. (Kota, 2009) represent the task
environment as a dynamically incoming stream of
tasks requiring multiple services. There is sequential
dependency between tasks. Kota represents tasks as
a tree of service instances (SIs) in which the parent
SI must be completed before the child SI. The Kota
model assigns tasks to the agents randomly, and the
assigned agent utilizes its subordinates, peers and
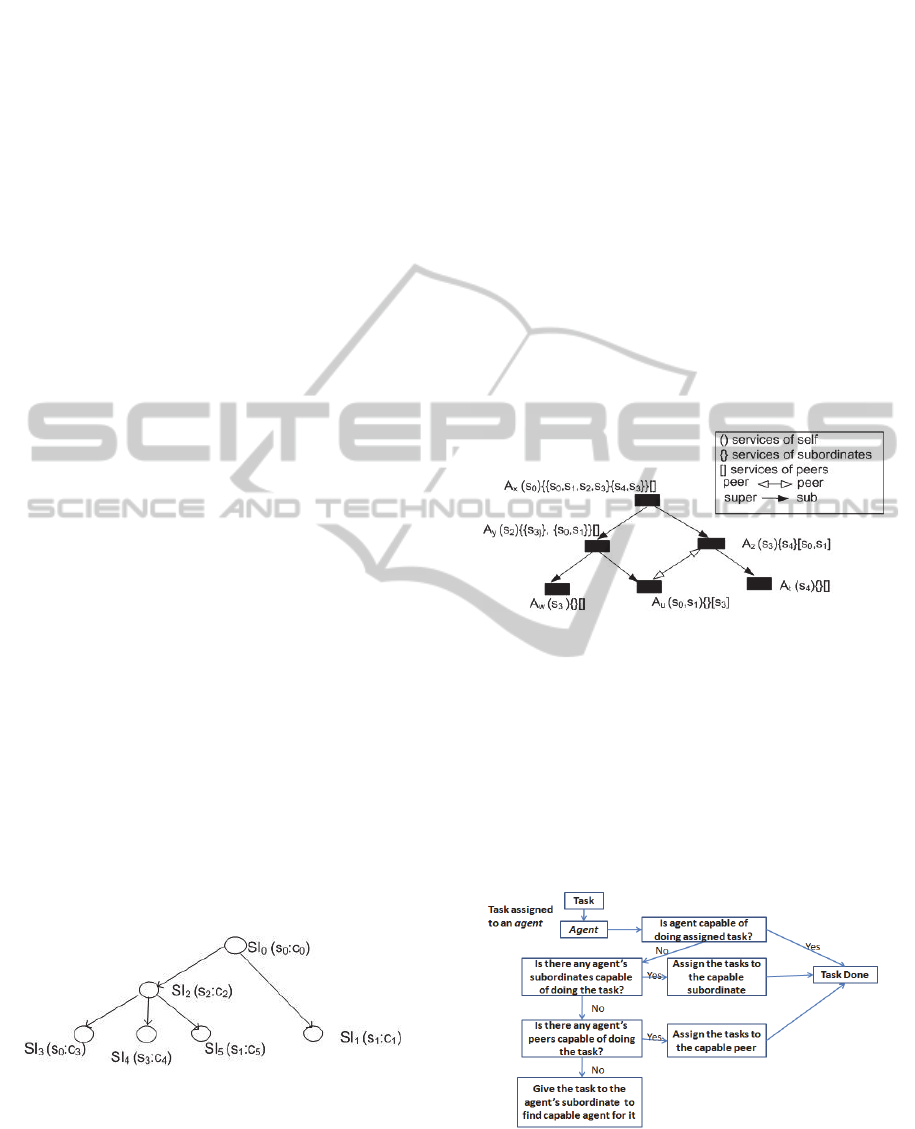
acquaintances to accomplish the task. Figure 1
demonstrates a tree of task dependencies.
Figure 1: Nodes represent a service instance (SI). Arrows
represent a dependency relationship. Each SI has a
provided service and a computational amount.
A tuple represents the services (skills) required
and the amount of computation needed for each of
the five SIs. Since finishing the task requires
multiple services, agents pass the task between
themselves in order to complete all of the services
required. The task is complete when its entire tree of
SIs has been executed.
In the Kota work, agents are known to each other
with three levels of relationship: (a) acquaintance
(knowing existence, but having no interaction), (b)
peer (low frequency of interaction) and (c) superior-
subordinate (preferred interaction). The superior-
subordinate relation is an authority relation as it
depicts the authority held by the superior agent over
the subordinate agent. The peer relation is present
between agents who are equal in authority with
respect to each other. The type of relationship
between agents determines both the allocation of SIs
and the amount of information agents know about
each other. Structure of the organization regulates
the interactions between agents. Figure2 shows an
example of the organizational structure of agents.
Figure 2: Example organizational structure.
In the Kota model, every agent has a fixed
number of services it can provide and a known
computational power. Thus, an agent is of the form
A
x
= <s
x
,c
x
> where s
x
S (S is the complete list of
services) and c
x
is the agent’s capacity in terms of
computational units in a time step. An agent prefers
to allocate the subtasks to its subordinate agents as
subordinate agents give priority to tasks assigned by
the superior. An agent will always try to execute an
Figure 3: Process of assigning a task to an agent.
SI if it contains the service and available
computational power. If it is not possible for the
agent to execute that SI, it can delegate it to one of
EfficientSelfAdaptingAgentOrganizations
295
its neighbours. Figure 3 shows the process of
assigning a SI.
Each agent can respond to only one request per
time-step. Therefore, agents store requests in a
waiting queue. Requests in a waiting queue are
considered in a first-come, first-served basis. Each
task has a deadline associated with it. If the agent
spends time on a task that is not finished, it gets
negative utility equal to the utility of the subtask. If
it does not attempt the task, there is no penalty as
there was no wasted effort. Also, each task has an
estimated amount of required time. The utility of the
task decreases if it takes more than the estimated
time. Equation1 shows the relationship between
utility and time. Here t stands for time.
(1)
When an agent is consistently looking for
another agent to perform a given service, it is
motivated to reorganize to form a direct relationship
with an agent providing that service. This process is
called adaptation. This process seeks continuously
to improve the profit of the system. Agents can
adapt only locally and change only their own links.
Though based on local adaptation by the agents, the
method should lead to the benefit of the organization
as a whole. The Adaptation process consists of two
main parts, named Meta-Reasoning and
Reorganization. Meta-Reasoning asks: ‘How many
agents should be considered by agent
x
for
reorganization?’ and ‘Which agents should be
selected among its neighbours?’ The number of
agents considered for reorganization at time t, k
t
, is
computed as showed in Equation2.
1
∗
,
(2)
In this Equation, L
x
is the computational capacity
of the agent
x
, l
x
is the current load on the agent and
R is the reorganization load coefficient, denoting the
amount of computational units consumed by an
agent while changing a single relation. acqts
x
represents the number of acquaintances of agent
x
,
changed
x,t−1
denotes the number of changed relations
of agent
x
in the previous iteration and k
t−1
denotes
the k value used in the previous iteration. Based on
Equation 2, at least one of the agent
x
’s neighbours is
considered for reorganization in each iteration. The
second term, which is
, indicates that
reorganization can consume the remaining
computational capacity of agent
x
in current iteration,
regardless of the need for that much reorganization.
The third term, which is
∗
,
,
estimates the number of relations which should be
considered for reorganization based on the history of
past iterations.
After finding the value of k
t
, agent
x
randomly
picks
agents from the list of its neighbors
including its peers, subordinates and acquaintances
for reorganization. In the Reorganization part of the
Kota method, agent
x
evaluates its relations with
considered agents in the Meta-Reasoning part. This
evaluation considers changing those relations to
another type of relation in order to increase profit.
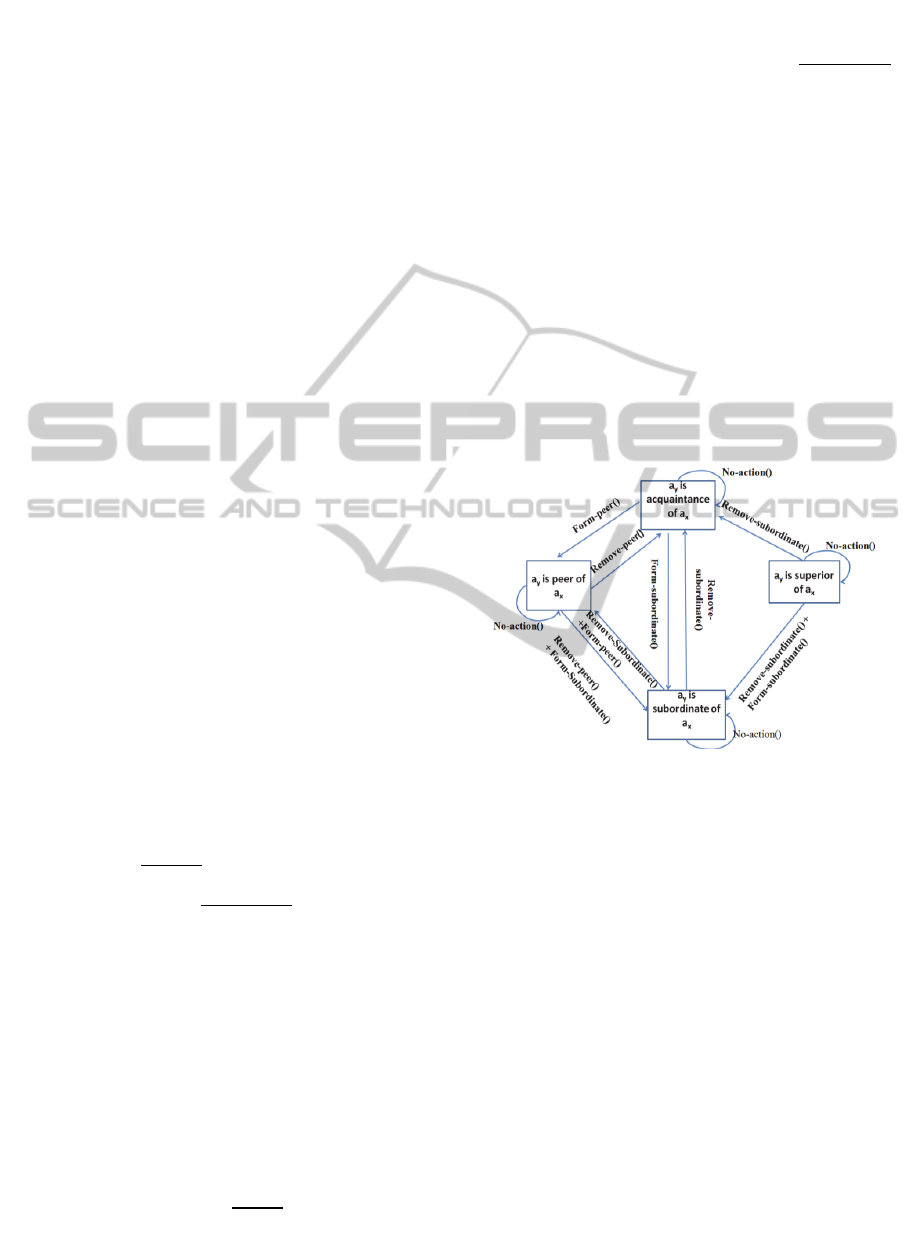
Figure 4 shows the possible actions between two
agents, dependent on the current relationship. Then
agent
x
evaluates the utility of each of the possible
actions. After calculating the utility of each action,
agent
x
selects the best reorganization action.
Figure 4: Diagram of Possible Actions.
One of the deficiencies of the Kota method is the
lack of a suitable task scheduling algorithm; tasks
are assigned to agents randomly. Randomly
assigning tasks increases the load on the assigned
agent when it cannot provide needed capabilities.
Figure 3 shows the process of finding a capable
agent in such a case. This approach adds
communication cost to the system and keeps the
assigned agent busy finding a capable agent.
Therefore, an intelligent way of task scheduling is
needed in order to improve the profit and reduce the
cost. Other deficiencies include randomly choosing
neighbours for reorganization and complex method
for evaluating possible actions.
3 OUR MODEL
In this research, we adopt the structural constraints
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
296

of the Kota research (Kota, 2009), but focus on the
deficiencies of its model. In our method, Selective-
Adaptation, each agent selects agents among its
neighbours based on different approaches. The
adaptation part of Selective-Adaptation method is
composed of two parts which are Meta-Reasoning
and Reorganization. The relation of an agent and its
neighbours is based on the two-way task passing.
Most of the time agents utilize the capabilities from
their neighbourhood subordinates and peers;
however, there are some cases in which agent’s
needs are not fulfilled using its peers and
subordinates. Therefore, an agent passes the request
back to its superior. Its superior is in charge of
finding a suitable agent for this request. Figure 3
summarizes the task passing mechanism; it shows
how an agent and its neighbours cooperate in
executing different parts of tasks.
We term service-providing agents (which are not
currently connected as a peer or superior/subordinate)
as outsideHelpers. Since the goal of adaptation is
promoting relations with agents who are useful to it,
we need to consider outsideHelpers. In this model, we
use the term neighbours for peers and subordinates of
agent
x
. In our system, an agent’s activities includes
executing tasks, management (communications,
evaluation of neighbours, task passing and updating
neighbour information) and reorganization. Load
refers to the computational units used to perform an
agent’s duties.
3.1 Meta-Reasoning
In Meta-Reasoning, each agent determines the
number of agents from its neighbourhood which
should be considered for reorganization.
Determining this number is critical because
evaluating too many agents wastes the resources of
the current agent. In addition, the agent needs to find
out which neighbours to consider for reorganization.
Meta-Reasoning used in this research is a history-
based process and utilizes different approaches
namely Fixed approach, Need-Based approach,
Performance-Based approach and Satisfaction-based
approach. We discuss these approaches in the
following subsections.
3.1.1 Fixed Approach
In the Fixed approach, agents have an opportunity to
evaluate their relationship with their neighbours in
all iterations. Our experiments show that the cost of
reorganization is one of the most important factors
that affect profit of the system. In order to increase
the profit, each agent needs the most useful
neighbours. The best neighbours are the ones that
result in a higher utility for the system. In order to
make reasonable decisions about reorganization, the
reorganization load coefficient, R, has been defined
(Kota, 2009). Evaluating many relationships might
exhaust the resources of the agent. Thus, agent
x
has
to restrict the set of its neighbours to consider for
reorganization. Agent resources include
computational capacity (which is used in each cycle
and does not roll over to next iteration) and
computational power. These types of resources are
distinct. Computational capacity must be consumed
in each iteration or it is lost. Computational power
represents a separate resource which can be saved
between iterations (like gasoline for a car). Agents
are recharged with computational power every d
time steps. Agents use the recharge interval to
estimate how much of the resource can be consumed
in any iteration. Since fuel costs are not negligible,
the use of fuel should be wisely monitored. This
amount is kept in InitialComp variable. Since agents
execute their assigned tasks first in each iteration
and then they go to the reorganization phase, the
remaining computational capacity of each iteration
after executing tasks can be used on reorganization.
By dividing the amount of remaining computational
power by R, the number of agents that can be
considered for reorganization is determined and
stored in k
t
. Equations 3 and 4 show the process of
determining k
t
. In these equations, i stands for
current iteration and RemComp indicates the
remaining power of iteration.
(3)
⁄
(4)
The number of agents to be considered for
reorganization, k
t,
should be divided between
neighbours and outsideHelpers of agent
x
. For this
division, we use the fraction w
f
to determine the
proportion of agents in each category based on
Equation 5 and 6.
w
∗numAgents
(5)
k
(6)
We found that the system reached highest profit
when w
f
=0.3. Thus, 30 percent of agents we consider
for reorganization are from outsideHelpers and the
rest are agent
x
’s neighbours. Figure 5 shows the
pseudocode of the Fixed approach algorithm. The
strategy of agent
x
in selecting the most suitable
outsideHelpers and most suitable neighbours is
different. Agent
x
calculates earned utility of its
neighbours and ranks them by this attribute. The
more utility they have earned, the better rank they
EfficientSelfAdaptingAgentOrganizations
297

have. Agent
x
tries to replace some of its inefficient
neighbours, but makes a stronger link with
acquaintances which were helpful in the past.
Fixed Approach
1. k
t
=agent
x
. calcNumAgents();
2. numOutsideH= agent
x
.calcNumOutsideH(w
f
);
3.numNeighbors=k
t
- numOutsideH;
4.OH= agent
x
.findBestOutsideH(numOutsideHelper);
5.N=agent
x
.findWorstNeighbors(numNeighbors);
6.AgentsToConsider= agent
x
.combine(OH,N);
Figure 5: Pseudocode of Fixed-Approach.
3.1.2 Need-Based Approach
In the Need-Based approach, at each iteration, agent
x
estimates the number of links it needs to reorganize
using two parameters from past iterations: 1) the
number of relations considered for reorganization,
and 2) the number of relations changed in past
iterations. By dividing the number of relations
changed by the number of relations considered,
agent
x
can estimate how many of its past predictions
have been accurate. Therefore, k
t
estimates the
number of agents which need to be considered in the
current iteration (t) based on Equation 7. After
deciding the number of agents to be considered, (k
t
),
agent
x
needs to divide k
t
between its neighbours and
outsideHelpers using equations 5 and 6.
∑
∑
∗ (7)
By testing different values for w
f
, the system reaches
the highest profit where w
f
=0.3. Neighbours and
outsideHelpers get their rank based on their earned
utility for agent
x
. Figure 6 shows the pseudocode of
this approach.
NeedBased Approach
1.k
t
=agent
x
. calcNeedBasedNumAgents();
2.numOutsideH= agent
x
.calcNumOutsideH(w
f
);
3.numNeighbors=k
t
- numOutsideH;
4.OH= agent
x
.findBestOutsideH(numOutsideH);
5.N=agent
x
.findWorstNeighbors(numNeighbors);
6.AgentsToConsider= agent
x
.combine(OH,N);
Figure 6: Pseudocode of Need-BasedApproach.
3.1.3 Performance-Based Approach
In the Performance-Based Approach, we utilize a
measure of performance to decide which agents to
consider for reorganization. Each task in the system
has an assigned utility. When an agent is assigned a
task, this agent can earn the whole utility of the task.
Therefore the possible utility agent
x
can earn would
be sum of the utilities of all tasks it has been
assigned as shown in Equation 8. Sometimes agents
cannot earn that amount of possible utility due to the
features like deadline violation and slowness in
completing tasks. The amount of utility earned in
comparison with the possible utility available can be
a good measure of performance for agents.
∑
∈
(8)
∑
∑
(9)
Equation 9 shows the measure of performance.
for each agent based on its history of earning utility.
In this equation i stands for any previous iteration,
and t indicates current iteration. The history variable,
h, indicates the number of past iterations to consider
and is in the range of [1, t-1], where h=t-1 considers
the history of all iterations so far, and h=1uses only
the history of the last iteration. In this approach,
agent
x
, finds the performance for all of its
neighbours and outsideHelpers. Then agent
x
selects
w
i
ratio of its worst neighbours in terms of
performance along with w
o
ratio of its best
outsideHelpers in terms of their performance. For
setting the values of w
i
and w
o
, we tested the system
with different values and compared the results. In
this case, system reaches highest profit in w
i
=0.25
and w
o
=0.15, which means that 25 percent of least
efficient neighbours of agent
x
along with 15 percent
of best outsideHelpers have been selected. If agent
x
does not have any outside helpers, it just considers
its neighbours for reorganization. Figure 7 shows the
Performance-Based approach.
Performance-Based Approach
1.s1=agent
x
.leastEffecient(neighbors,w
i
);
2.if count(outsideHelpers)>0
3. outsideH= agent
x
. findOutsideHelpers();
4. s2=agent
x
.mostEffecient(outsideH,wo);
5. agentsToConsider= agent
x
.combine(s1,s2);
6.else
7. agentsToConsider= s1;
Figure 7: Pseudocode of Performance-Based Approach.
3.1.4 Satisfaction-Based Approach
In the Satisfaction-Based approach, agents decide on
the adaptation based on satisfaction. As we
mentioned earlier, the relation of an agent and its
neighbours is based on subtask passing. Each agent
is satisfied with a relation when the corresponding
agent is able to service most of the agent’s requests;
the stronger neighbourhood in terms of providing
requests, the more satisfied agent is. When an agent
accepts a subtask request, it means that it has the
potential to accomplish that subtask. To compare
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
298

agents in the neighbourhood, we define a measure of
satisfaction as shown in Equation 10.
∑
∑
(10)
In this equation, i stands for iteration and t
indicates current iteration. Variable h is in the range
of [1, t-1] as before. In satisfaction based approach,
agent
x
calculates the satisfaction of all its neighbours
and its outsideHelpers. Based on this measure,
agent
x
selects w
i
ratio of its least satisfactory
neighbours to be considered for reorganization. If
there are any outsideHelpers, agent
x
needs to select
w
o
ratio of its most satisfactory outsideHelpers for
reorganization too. Values of w
i
and w
o
are set same
as Performance-Based approach. Figure 8 illustrates
the pseudocode this approach.
Satisfaction-Based Approach
1.s1=agent
x
.leastSatisfactory(neighbors,w
i
);
2. if count(outsideHelpers)>0
3. outsidH= agent
x
. findOutsideHelpers();
4. s2=agent
x
.mostSatisfactory(outsidH,w
o
);
5. agentsToConsider= agent
x
.combine(s1, s2);
6. else
7. agentsToConsider= s1;
Figure 8: Pseudocode of Satisfaction-based Approach.
For all approaches, we need to set the value of h.
Our experiments show that considering total number
of past iterations (h=t-1) is too much history and
considering the history of last iteration (h=1) may
give a little insight about the past. We tested
different values for h and our experiments show that
in h=10 system reaches highest profit.
3.2 Reorganization
The second part of our Selective-Adaptation
approach is Reorganization. Reorganization enables
an agent to change its relations with some of its
neighbours (kept in AgentsToConsider list) which
are identified in the MetaReasoning step.
In this phase, agent
x
evaluates all of the possible
types of relation for each member of
AgentsToConsider and changes the relations in order
to achieve a higher utility. For each agent
i
in this list,
agent
x
takes the best action among possible actions
based on the current relationship and a measure
computed from some evaluation functions. Figure 4
demonstrates possible actions for two agents based
on their current relation. Figure 9 shows the
pseudocode of the reorganization part.
Reorganization changes the current relation type
R
c
to a new relation type R
n
. Note that if the
Reorganization Part
1.for agent
i
in agentsToConsider
2. possible=agent
x
.findPossibleActions(agent
i
);
3. desiredAction=agent
x
.evaluate(possible);
4. if desiredAction !=no-Action
5. agent
x
.takeAction(agent
i
, desiredAction);
Figure 9: Pseudocode of Reorganization part.
selected action is “NoAction” then R
n =
R
c
(which
means that relation will not change and this action
does not have utility and cost). The most important
part of the reorganization approach is evaluating the
utility of possible actions and choosing the best one.
Kota method’s evaluation function uses
parameters like:1) the number of subtasks assigned
by agent
x
to agent
y
, 2) the number of subtasks
delegated by agent
x
to agent
y
, 3) the total number of
time-steps that agent
x
existed, 4) the number of time-
steps that agent
x
and agent
y
had a superior-
subordinate relation or peer relationship, 5) the
number of time-steps out of the total time that agent
x
had waiting tasks, 6) the total number of subtasks
agent
x
assigned to other agents and 7)the
communication cost due to the delegations from by
agent
x
to agent
y
. Kota method’s evaluation function
is overly complex. Selective-Adaptation needs less
data but makes good decisions.
The profit of an agent from the action act
d
is
calculated using Equation 11. Based on Equation 11,
the profit of each action consists of two terms,
Utility and Load. This equation is used for both
forming and removing a relation. In forming a
desirable relation, the sign of Utility is positive. As
any new relation adds some load to the agent, the
sign of Load is negative. The signs are reversed in
the case of removing a relation.
(11)
(12)
In forming a relation, to estimate the utility for
agent
x
in the process of changing the relation with
agent
y
(from R
c
to R
n
), two terms are used: 1) the
average utility agent
x
earned from agents which were
in the same relation type as R
n
which is called
and 2) the average utility agent
x
earned from agent
y
which is called
. Equation 12 shows
this approach. For example, if agent
x
wants to make
a peer relation with agent
y
, it calculates the average
earned utility of its peers so far (
) along with the
average utility earned form agent
y
(
).
This equation says that for having relation type (R
t
)
with agent (a
y
), the experience of agent
x
from that
type of relation (R
t
) and the history of functionality
EfficientSelfAdaptingAgentOrganizations
299

of agent (a
y
) affect the decision. In a case of
removing a relation, for calculating Utility, we use
the Equation 12 too, but the value of
will be set as zero. The second term of Equation 11
is Load and includes different types of loads as
shown in Equation 13. M is the management load of
having a new relation, C is the communication cost
and R is the reorganization load coefficient.
(13)
We used the general term M and C in Equation
13, however, the management load and
communication cost depends on the type of relation
between two agents. Each agent estimates the
amount of M and C based on its history of this type
of relation if known. Table1 summarizes all the
loads that agent
x
(a
x
) experiences in changing a
relation with agent a
y
.
Table 1: Loads and Costs of a
x
related to different
relations.
M C R
a
x
is peer of a
y
M
peer
C
peer
R
peer
a
x
is subordinate of a
y
- C
subordinate
R
subordinate
a
x
is superior of a
y
M
su
p
erior
C
su
p
erior
R
su
p
erior
3.3 Task Scheduling
One of the deficiencies of the Kota method is its
inefficient task scheduling algorithm as it assigns
tasks to agents randomly. Random task assignment
increases the load on the assigned agents when they
are not capable. In this case, the assigned agent
needs to go to the process of finding capable agent
as depicted in Figure3.
Task Schedulling
1. CCList=findCompCapacityAgents();
2. QLList=findQueueLengthAgents();
3. SSList=findServicesSimilairity(Task);
4. suitableAgent=findSuitableAgent (CP,QL,SS);
Figure 10: Pseudocode of Task Scheduling Approach.
Random assignment also adds communication
cost to the system and keeps the responsible agent
busy finding a capable agent among its neighbours.
It wastes resources which the agent could use on
executing tasks. Therefore, an intelligent way of task
scheduling is crucial. In Selective-Adaptation, the
system tries to find the most suitable agent for task
assigning. Pseudocode of Task Scheduling is
outlined in Figure 10.To find the most suitable agent
for each task, we consider: 1) computational
capacity of agents, 2) queue length of agents (how
busy the agents are) and 3) similarity of services
(how many of the services needed for the task can be
provided by the agent).The most desirable agent is
the one which has the highest computational
capacity and similarity of services. In addition, it
needs to have a small queue length because if the
system assigns a task to a busy agent, the task may
wait a long time for execution. Since the goal of the
system is to reach a higher profit, wasting time in the
queue while there are other agents in the system
which can execute the task is not reasonable. The
length of the queue is determined by the summation
of the cycles required of each task in the queue.
Finding the most suitable agent is the duty of the
findSuitableAgent function in line 4 of the
pseudocode depicted in Figure 10. This function
aims to find an agent which is the best based on the
rank of Equation 14.
∗
∗
∗
(14)
In the Equation 14, CC stands for computational
capacity of each agent, QL indicates queue length
and SS stands for similarity of services. An agent
which gets the highest rank will be selected as the
most suitable agent. Our experiments reach the
highest profit when these terms had an equal effect
(
1
=
2
=
3
).
3.4 System Evaluation
We evaluate the effectiveness of models based on
the performance of their organization based on
Profit, which is the summation of the profits of all of
the individual agents. We examine the amount of
profit per iteration using Equation 15 in order to
determine if any improvement is achieved. Thus, for
finding the profit we need to compute the amount of
utility has been earned and total cost of that
iteration. The earned utility by a given agent will be
found using Equation 1.
ProfitUtilityEarned–TotalCost (15)
TotalCostReorgCostCommCost(16)
For finding TotalCost, Equation 16 will be used.
Equation 16 shows that costs in the system include
reorganization cost and communication cost.
Reorganization cost includes evaluating
relationships and changing relationships. The
process of assigning a task to an agent requires
sending and receiving messages to/from that agent.
Therefore, these processes also require inter-agent
communication which adds to the total cost of the
organization.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
300

4 EXPERIMENTS AND RESULTS
As we mentioned earlier Selective-Adaptation
method has four different approaches namely Fixed,
Need-Based, Performance-Based and Satisfaction-
Based. In our experiments, we show the behaviour
of each of these approaches, plus Kota method; for
each one, we averaged the results for 100
simulations of 1000 iterations. Note that for
simplicity, we just use the name of approaches of the
Selective-Adaptation in the figures, so when in a
figure we write Fixed approach we mean Fixed
Approach of Selective-Adaptation method.
4.1 Profit over Time
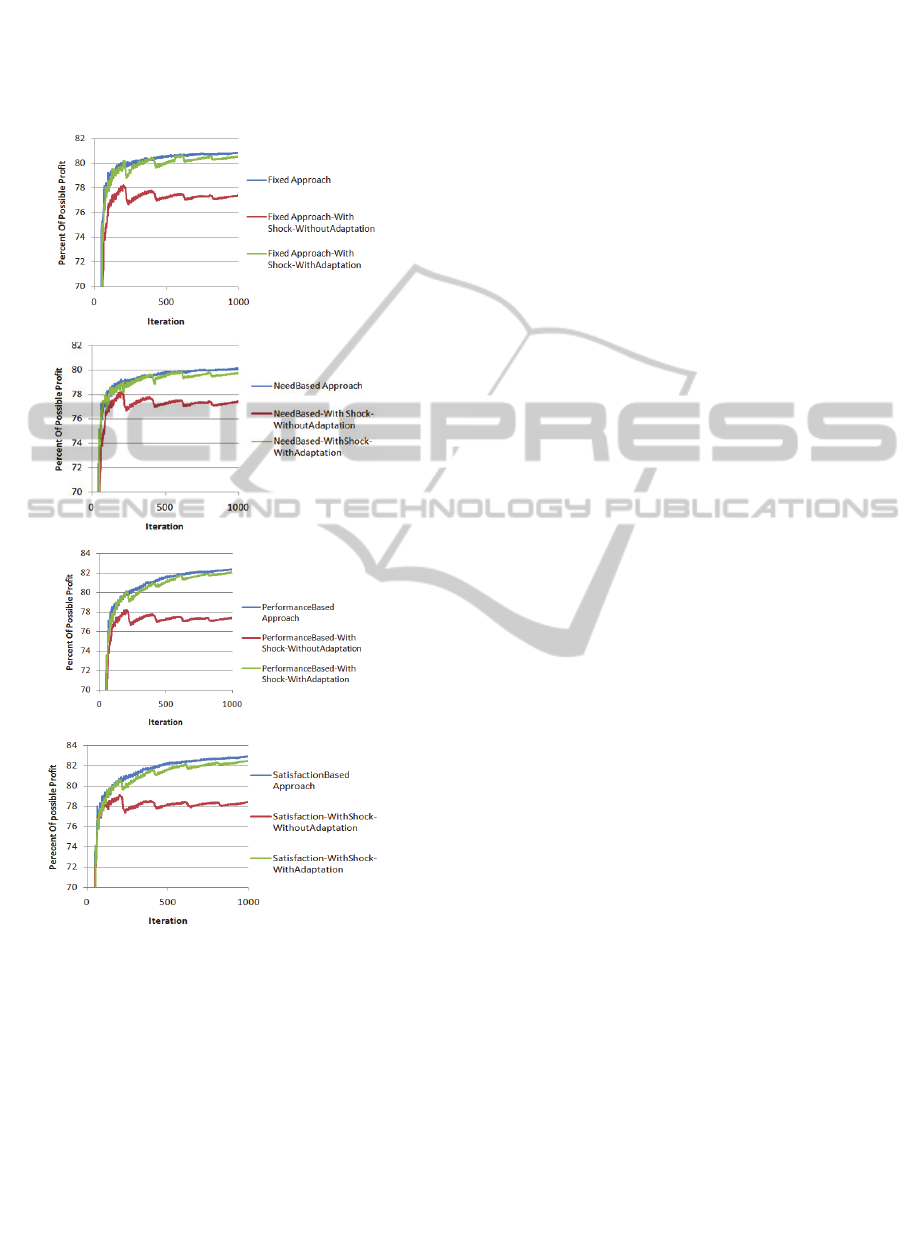
As can be seen from Figure 11, results show the
behaviour of different approaches of Selective-
Adaptation and Kota method.
Figure 11: Profit of different approaches over Iteration.
An identical reorganization part is used in all
Selective-Adaptation approaches; therefore the
different profit over time comes from their Meta-
Reasoning approaches. It seems that just using
history of past iterations in the Need-Based approach
is not effective as this approach has the worst
performance among all methods. Fixed approach’s
overall profit is better than Kota because it utilizes
an intelligent way of selecting neighbours for
reorganization. Among all methods of Figure 11
Performance-Based and Satisfaction-Based
approaches have better performance. Their
behaviour proves these approaches exploit more
applicable Meta-Reasoning approach. Since
Satisfaction-based approach outperforms all other
approaches, results suggest that using this approach
of Selective-Adaptation helps the system reaches
higher performance.
4.2 Effect of Task Scheduling
As discussed Selective-Adaptation method benefits
from intelligent way of task scheduling. Figure 12
shows the effect of task scheduling on the various
Selective-Adaptation approaches. As can be seen,
the task scheduling leads all of the approaches reach
higher profits.
Figure 12: Effect of task scheduling. From top to bottom
a)Fixed, b)Need-Based, c)Performance-Based and
d)Satisfaction-based approaches of Selective-Adaptation.
4.3 Shocks to the System
The aim of the adaptation method is to determine
and apply changes in the organization structure in
order to improve the performance. Adaptation needs
to respond to changes in the environment in a self-
organized manner. In order to see the behaviour of
adaptation facing unpredicted events, we impose
shocks upon the system.
EfficientSelfAdaptingAgentOrganizations
301
4.3.1 Agent Shock Experiment
Agents are associated with particular sets of
services. These sets can be overlapping; that is, two
or more agents may provide the same service.
Figure 13: Effect of Agent Shock. From top to bottom
a)Fixed, b)Need-Based, c)Performance-Based and
d)Satisfaction-based Approaches of Selective-Adaptation.
Different tasks require different amounts of time,
and the load requirement is not uniform; therefore
agents use a queue to store tasks which are waiting
for service.
In our experiment with agent shock, every 200
iterations 1/5 of the agents are disabled. Because of
this, disabled agents’ peers and subordinates bear
more load. They need to distribute disabled agents
queue among other agents which are capable of
performing the tasks. After 15 iterations, new agents
will be added to the system to replace the disabled
agents. New agents (which need to be incorporated
into the organization structure) are added as
acquaintances to all other agents. Figure 13 shows
the effect of Agent Shock on different methods. As
we discussed earlier, main goal of adaptation is
continuously improve the profit of the system.
Therefore, in these experiments after passing shock
periods, there are improvements due to adaptation in
comparison with the case without adaptation. We
show that adaptation handles unexpected shocks to
the system and compensates for the perturbations.
4.3.2 Task Shock Experiment
Tasks have some patterns in the dependency links
between the SIs. In this way, the dependencies
between the SIs may follow some frequent orderings
(resulting from the dependencies internal to a pattern
occurring in several tasks). For the shock test, we
defined four different patterns between tasks. Every
200 iterations, we change the pattern to see the
effect of the shock. Each agent creates its
neighbourhood based on the needed capabilities. In
the case of changing the pattern, agents must adapt
to the lack of capability among their neighbours. In
such a case, the profit of the system decreases as it
can be seen in Figure14, Agents’ queues become
longer and all of the agents are busy with passing
tasks in order to find suitable agents for their
assigned tasks. After some iterations utilizing
adaptation, the system compensates for what it lost
during shock time by making new neighbourhood
based on the new pattern. Improvements due to
adaptation are easily distinguishable. As mentioned
earlier, the difference between various approaches of
Selective-Adaptation is in the adaptation part.
Therefore if we disable the adaptation part, all the
approaches of Selective-Adaptation have the same
behaviour; Figure 13 and Figure 14 illustrate this.
5 CONCLUSIONS
In this paper, we propose a new method of
adaptation which is called Selective-Adaptation. We
demonstrate a robust, decentralized approach for
structural adaptation organizations. Our adaptation
method is based on the agents forging and dissolving
relations with other agents. Agents use the history of
past iterations as a measure of evaluation. This
method consists of two parts namely Meta-
Reasoning and Reorganization. In the Meta-
Reasoning, every iteration each agent selects some
of its neighbours for reorganization based on
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
302
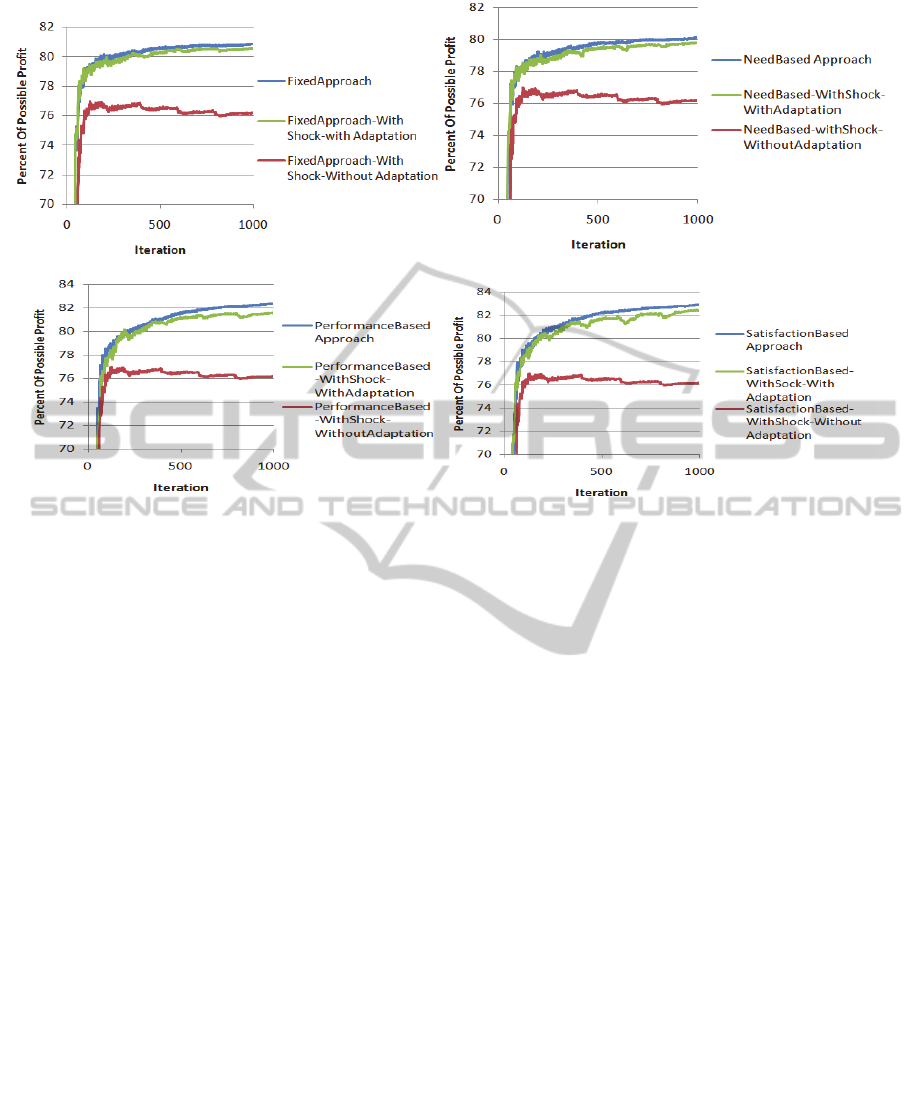
(a) (b)
(c) (d)
Figure 14: Effect of Task Shock. a)Fixed, b)Need-Based, c)Performance-Based and d)Satisfaction-based Approaches of
Selective-Adaptation.
approaches: 1)Fixed approach, 2)Need-Based
approach, 3) Performance-Based approach, and 4)
Satisfaction-based approach. After selecting
neighbours, the agent tries to find all of the possible
actions between itself and target agent based on the
current relationship between them. Then, the agent
evaluates all of the possible actions and selects the
best one in terms of its estimated utility. This
method can successfully handle unexpected shocks
to the system, along with showing higher profit in
comparison with other existing methods of self-
organization. Possible future work includes
restricting agents’ resources like the amount of
memory agents can use for keeping information
about others and considering network bandwidth.
ACKNOWLEDGEMENTS
This work is supported by NSF research
grant#0812039 entitled “Coalition Formation with
Agent Leadership”.
REFERENCES
R. Kota, et al. (2009). ‘Self-organising agent
organisations'. In 8th Conference on Autonomous
Agents and Multiagent Systems - Volume 2, AAMAS
'09, pp. 797-804, Richland, SC.
C. Sansores& J. Pavón (2008).‘An adaptive agent model
for self-organizing MAS'. In the 7th international
conference on Autonomous agents and multiagent
systems - Volume 3, AAMAS '08, pp. 1639-1642,
Richland, SC.
J. C. Miralles, et al. (2009). ‘Multi-agent system
adaptation in a peer-to-peer scenario'. In the 2009
ACM symposium on Applied Computing, SAC '09, pp.
735-739, New York, NY, USA.ACM.
L. Barton & V. H. Allan (2008).‘Adapting to Changing
Resource Requirements for Coalition Formation in
Self-Organized Social Networks'. In the 2008
IEEE/WIC/ACM International Conference on Web
Intelligence and Intelligent Agent Technology -
Volume 02, WI-IAT '08, pp. 282-285, Washington,
DC, USA.IEEE Computer Society.
W. Zheng-guang& L. Xiao-hui (2006). ‘A Graph Based
Simulation of Reorganization in Multi-agent Systems'.
Intelligent Agent Technology, 2006. IEEE/WIC/ACM
International Conference, pp. 129-132.
J. M. Alberola, V. Julian, and A. Garcia-Fornes,
"Multidimensional adaptation in MAS organizations,"
IEEE Transactions on Systems, Man, and Cybernetics,
Part B (Cybernetics), pp. 1-12, 2012.
D. Ye, M. Zhang, and D. Sutanto, "Self-organization in an
agent network: A mechanism and a potential
application, “Decision Support Systems, vol.53, no
3pp. 406-417, Jun. 2012.
EfficientSelfAdaptingAgentOrganizations
303
