
Iterative Possibility Distributions Refining in Pixel-based Images
Classification Framework
B. Alsahwa
1,2
, S. Almouahed
1
, D. Guériot
1,2
and B. Solaiman
1,2
1
Image & Information Processing Dept., Telecom Bretagne, Institut Mines-Télécom, Brest, France
2
Lab-STICC UMR CNRS 3192 - Laboratoire en Sciences et Technologies de L'information, de la Communication
et de la Connaissance (Institut Mines-Télécom-Télécom Bretagne-UEB), Brest, France
Keywords: Possibility Theory, Incremental Learning, Possibilistic Seed, Possibilistic Decision Rule, Possibilistic
Confidence Threshold.
Abstract: In this study, an incremental and iterative approach for possibility distributions estimation in pixel-based
images classification context is proposed. This approach is based on the use of possibilistic reasoning in
order to enrich a set of samples serving for the initial estimation of possibility distributions. The use of
possibilistic concepts enables an important flexibility for the integration of a context-based additional
semantic knowledge source formed by pixels belonging with high certainty to different semantic classes
(called possibilistic seeds), into the available knowledge encoded by possibility distributions. Once
possibilistic seeds are extracted, possibility distributions are incrementally updated and refined. Synthetic
images composed of two thematic classes are generated in order to evaluate the performances of the
proposed approach. Initial possibility distributions are, first, obtained using a priori knowledge given in the
form of learning areas delimitated by an expert. These areas serve for the estimation of the probability
distributions of different thematic classes. The resulting probability density functions are then transformed
into possibility distributions using Dubois-Prade’s probability-possibility transformation. The possibilistic
seeds extraction process is conducted through the application of a possibilistic contextual rule using the
confidence index used as an uncertainty measure.
1 INTRODUCTION
An accurate and reliable image classification is a
crucial task in many applications such as content
based image retrieval, medical and remote-sensing
image analysis. An important difficulty related to
this task stems from the inability, in most situations,
to have a representative knowledge of different
thematic classes contained in the analyzed scene.
This is mainly due to the fact that this task is time-
consuming and to the lack of solid knowledge
ensuring the representative constraints of the
available knowledge. Hence, starting from a limited
initial prior knowledge, an efficient classifier is
assumed to have the capacity of extracting additional
knowledge with a high degree of confidence while
preserving the previously acquired knowledge.
Focusing the attention on knowledge refining
type in classification systems as the target of the
incremental learning process, few approaches can be
encountered in the literature: incremental-learning
neural networks for remote-sensing images
classification (Bruzzone and Fernàndez, 1999)
where the parameters of the existing kernel functions
are refined. Refining possibility distributions using
the incremental-learning fuzzy pattern matching
(FPM) is also proposed for diagnosis in industrial
and medical applications (Mouchaweh et al., 2002).
However, all encountered approaches have some
limitations: a) The class labelling of each new
sample is conducted without taking into account the
importance of the contextual information mainly in
the context of noisy images classification (Tso and
Mather, 2009); b) The knowledge refining process is
done after the addition or classification of each new
sample which may be a drawback. In order to
overcome the limitations of the above mentioned
approaches, an incremental and iterative approach
for possibility distributions estimation in pixel-based
images classification context is proposed under the
closed world assumption. This approach is based on
the use of possibilistic reasoning concepts in order to
176
Alsahwa B., Almouahed S., Guériot D. and Solaiman B. (2013).
Iterative Possibility Distributions Refining in Pixel-based Images Classification Framework.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 176-181
DOI: 10.5220/0004264901760181
Copyright
c
SciTePress

enrich the set of samples serving for the construction
of the initial possibility distributions.
Each pixel from the analyzed image, I, is
assumed to belong to one, and only one, thematic
class from an exhaustive set of M predefined and
mutually exclusive classes Ω = {C
1
, C
2
, ..., C
M
}.
Prior knowledge is assumed to be given as an initial
set of learning areas extracted from the considered
image and characterizing the M considered classes
(from the expert point of view). Based on this prior
knowledge, M class probability density functions
are, first, estimated using the KDE (Kernel Density
Estimation) approach (Epanechnikov, 1969) and,
then, transformed into M initial possibility
distributions encoding the “expressed” expert
knowledge in a possibilistic framework. The
application of the M class possibility distributions on
the considered image I will lead to M possibilistic
maps PM
I,C
m
, m= 1, ..., M where (PM
I,C
m
encodes
the possibility degree of different image pixels to
belong to the thematic class C
m
). Based on the use of
a degree of confidence, the extraction of new
learning samples is conducted using possibilistic
spatial contextual information, i.e. applied on
different possibilistic maps. The extraction process
is then iteratively repeated until no more new sample
can be added to the incremental learning process.
The use of a possibilistic reasoning approach
increases the capacity as well as the flexibility to
deal with uncertainty when the available knowledge
is affected by different forms of imperfections:
imprecision, incompleteness, ambiguity, etc. Notice
that, even when the used prior knowledge is perfect,
the additional knowledge extracted through any
incremental process may be affected by different
forms of imperfection (Hüllermeier, 2003).
In the next section, a brief review of basic
concepts of possibility theory is introduced. The
proposed iterative approach will be detailed in the
third section. Sections 4 and 5 are devoted to the
experimental results obtained when the proposed
approach is applied using synthetic as well as real
images.
2 POSSIBILITY THEORY
Possibility theory was first introduced by Zadeh in
1978 as an extension of fuzzy sets and fuzzy logic
theory to express the intrinsic fuzziness of natural
languages as well as uncertain information (Zadeh,
1978). In the case where the available knowledge is
ambiguous and encoded as a membership function
into a fuzzy set defined over the decision set, the
possibility theory transforms each membership value
into a possibilistic interval of possibility and
necessity measures (Dubois and Prade, 1980).
2.1 Possibility Distribution
Let us consider an exclusive and exhaustive universe
of discourse Ω = {C
1
, C
2
,..., C
M
} formed by M
elements C
m
, m = 1, ..., M (e.g., thematic classes,
hypothesis, elementary decisions, etc).
Exclusiveness means that one and only one element
may occur at time, whereas, exhaustiveness refers to
the fact that the occurring element belongs to Ω. A
key feature of possibility theory is the concept of a
possibility distribution, denoted by , assigning to
each element C
m
a value from a bounded set
[0,1] (or a set of graded values). This value (C
m
)
encodes our state of knowledge, or belief, about the
real world representing the possibility degree for C
m
to be the unique occurring element.
2.2 Possibility and Necessity Measures
Based on the possibility distribution concept, two
dual set measures, the possibility Π and the necessity
Ν measures are derived. For every subset (or event)
A, these two measures are defined as follows:
m
C
m
() maxπ(C )
A
A
(1)
m
C
m
N( ) 1 ( ) min 1 π(C )
C
A
AA
(2)
where, A
c
denotes the complement of A.
2.3 Possibility Distributions Estimation
based on Pr- Transformation
A crucial step in possibility theory applications is
the determination of possibility distributions. Two
approaches are generally used for the estimation of a
possibility distribution. The first approach consists
on using standard forms predefined in the
framework of fuzzy set theory for membership
functions (i.e. triangular, Gaussian, trapezoidal,
etc.), and tuning the form parameters using a manual
or an automatic tuning method.
The second possibility distributions estimation
approach is based on the use of statistical data where
an uncertainty function (e.g. histogram, probability
distribution function, basic belief function, etc.); is
first estimated and then transformed into a
possibility distribution
IterativePossibilityDistributionsRefininginPixel-basedImagesClassificationFramework
177

As we consider, in this study, that the available
expert’s knowledge is expressed through the
definition of learning areas representing different
thematic classes, i.e. statistical data, we will focus
on the second estimation approach. Several Pr-
transformations are proposed in the literature.
Dubois et al. (Dubois and Prade, 1983) suggested
that any Pr- transformation of a probability
distribution function, Pr, into a possibility
distribution, , should be guided by the two
following principles:
The probability-possibility consistency
principle.
() Pr(), AAA
(3)
The preference preservation principle
Pr( ) Pr ( ) ( ) ( ), , AB ABAB
(4)
The transformation Pr-suggested by Dubois et
al., is defined by:
M
mm j m
j=1
π(C )= (C )= minPr(C ), Pr(C )
(5)
In our study, this transformation is considered in
order to transform probability distributions into
possibility distributions.
2.4 Possibilistic Decision Rules
2.4.1 Maximum Possibility Decision Rule
The decision rule based on the maximum of
possibility is certainly the most widely used in
possibilistic classification/decision making
applications. This rule is based on the selection of
the elementary decision A
m
0
= {C
m
0
} with the
highest possibility degree of occurrence:
(R1): Decision = A
m
0
if and only if
Π(A
m
0
) = max
m=1, ..., M
[Π(A
m
)] (6)
2.4.2 Maximum Confidence Index Decision
Rule
Other possibilistic decision rules using uncertainty
measures are also developed. The most frequently
encountered rule (proposed by S. Kikuchi et al.
(Kikuchi and Perincherry, 2004)) is based on the
maximization of the confidence index Ind for each
event A
Ind : 2
→ [-1, +1],
A→
() () N() – 1Ind A A A , A
(7)
where 2
denotes the power set of
Notice that restricting the application of this
measure to events having only one element A
m
=
{C
m
} results in the following interesting property:
I
nd(
A
m
) =
(
A
m
) + N(
A
m
) -1
mn
mn
= π(C ) – π(C )max
(8)
This means that Ind(A
m
) measures the difference
between the possibility measure of the event A
m
(which is identical to the possibility degree of the
element C
m
) and the highest possibility degree of all
elements contained in /A
m
(i.e. the complement of
A
m
) (figure 1).
Figure 1: Confidence indices associated with different
decisions (A
m
0
: event having the highest possibility
degree, A
m
1
: event with the second highest possibility
degree).
The decision rule associated with this index can be
formulated by:
(R2): Decision = A
m
0
iff
Ind(A
m
0
) = max[Ind(A
m
)] , m=1, ..., M (9)
This decision rule associated with (R2) can be
more severe by accepting the decision making only
when the index value Ind(A) exceeds a predefined
threshold S (called possibilistic confidence
threshold):
(R2- Rejection): Decision = A
m
0
iff
mm
0
m
0
( ) max[ ( )], m=1, ..., M
( ) S
Ind A Ind A
Ind A
Decision= Rejection if Ind (A
m
) < S,
(10)
3 POSSIBILISTIC SEEDS
EXTRACTION RULES
In this study, the following possibilistic seeds
extraction rules are proposed and evaluated:
A. Pixel-based extraction rule:
This seeds extraction rule considers that a pixel
Ind(A
m
0
)
Ind(A
m
1
)
Ind
+1 -1
0
(C
m
0
)-
(C
m
1
)
(C
m
1
)-
(C
m
0
)
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
178
P
0
I is a possibilistic seed if its highest confidence
index value exceeds the threshold S[0,1]:
P
0
I is a possibilistic seed if
C
m
0
Ind(A
m
0
) ≥ S
(11)
B. Contextual-possibilistic extraction rule:
This rule duplicates the pixel-based extraction
rule but with the major difference of using, for each
pixel P
0
, the contextual-based possibility distribution
0
P
=[
0
P
(C
1
),
0
P
(C
2
), …,
0
P
(C
M
)] instead of
the pixel-based possibility distribution
P
0
=[
P
0
(C
1
),
P
0
(C
2
), …,
P
0
(C
M
)]. where
0
P
(C
m
), m = 1, 2, …,
M, is extracted from the m
th
possibilistic maps by
the application of a smoothing filter. In this study,
the mean smoothing filter is used; this leads to:
Pm ,C
m
0
P(P)
0
1
(C ) (P)
I
V
PM
N
(12)
where V(P
0
) refers to the considered contextual
neighborhood of the pixel P
0
and N is Card(V(P
0
)).
Using
0
P
a contextual confidence index Ind can
be computed for each class C
m
. The extraction rule
considers that a pixel P
0
I is a possibilistic seed if
P
0
I is a possibilistic seed if C
m
0
Ind (A
m
0
)=
P
0
(C
m
0
)-
mm
0
max
0
P
(C
m
) ≥ S
(13)
Using the learning zones, the initial estimation of
the class probability distribution functions are
established. The application of the Pr- Dubois-
Prade’s transformation allows obtaining the initial
possibility distributions (figure 3).
Using the learning zones, the initial estimation of
the class probability distribution functions are
established. The application of the Pr- Dubois-
Prade’s transformation allows obtaining the initial
possibility distributions (figure 3).
4 ITERATIVE POSSIBILISTIC
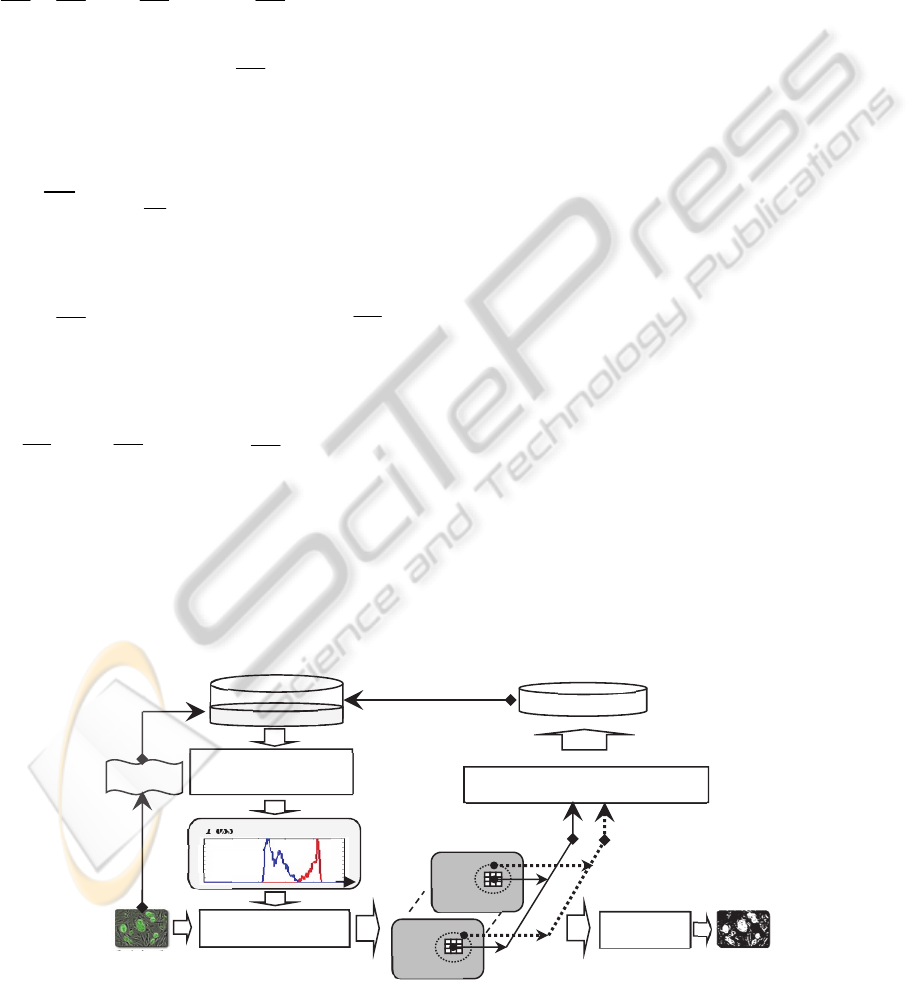
REFINING APPROACH
As previously detailed, the samples initial set U
0
,
considered by the expert, is used in order to estimate
the probability distribution functions of different
thematic classes, which in turns are transformed into
possibility distributions through the application of
the Pr- Dubois-Prade’s transformation.
At iteration “n”, the application of the
possibilistic seeds extraction rule produces the
additional set of seeds
U
n+1
. This seeds set is then
used to enrich the samples set
U = U
k
used
for the possibility distributions estimation (figure 2).
The seeds enrichment process is then iteratively
repeated until no more seeds are added.
5 EXPERIMENTAL RESULTS
5.1 Simulated Data
For the experimental evaluation purpose, a 96×128
pixel synthetic image composed of two classes
{C
1
,C
2
}, is generated(figure 3). Pixels from C
1
and
C
2
are generated as two Gaussian distributions
G(m
1
=130, σ
1
=15) and G(m
2
=100, σ
2
20).
Figure 2: Iterative possibilistic refining approach.
n + 1
k = 0
Original
Image
Possibility distributions
1
0
C
M
C
1
Possibilistic Knowledge
Projection
Possibilistic
Classification
Thematic
I
ma
ge
PM
I,C
1
PM
I,C
M
U
0
Possibility distributions
E
stimation
Possibilistic Seeds Extraction
U
n+1
E
xper
t
U
IterativePossibilityDistributionsRefininginPixel-basedImagesClassificationFramework
179

Figure 3: Synthetic image with learning zones and initial
possibility distributions (two Gaussian generated thematic
classes).
5.2 Possibilistic Seeds Extraction Rules
Evaluation
The proposed iterative approach is applied to the
analyzed image using each of the two proposed seeds
extraction rules. Two configurations have been tested:
in the first one, only the pixel value is taken into
account (no neighborhood) while in the second one, a
3x3 pixel window centered on each pixel is
considered as the local spatial possibilistic context. In
figure 4 and 5, for both configurations, the number of
correctly selected as well as erroneously selected
seeds are given for the previously mentioned
extraction rules as a function of the possibilistic
confidence threshold S[0,1] after convergence.
As our main target is to obtain a full truthiness of
the class membership for all the selected seeds, it
seems clear that restricting the extraction rule to
only pixel-based possibilistic knowledge level does
not fit into the targeted objective. On the other hand,
the contextual possibilistic seeds extraction rule
fulfills the aforementioned objective. An important
constraint, targeted by the proposed approach,
consists in having a fixed possibilistic confidence
threshold for different class distributions. Therefore,
it seems natural to fix the threshold into the mean
confidence interval value, i.e. S = 0.5. Having a risk
margin interval [0.45, 0.55], it seems that the
contextual possibilistic extraction rule never
produces erroneously extracted seeds (this result has
been verified using a huge amount of generated
images with different parameters and repeated for
several statistical distributions realizations).
Figure 4: Number of correct and erroneous selected seeds
for the pixel-based extraction rule.
Figure 5: Number of correct and erroneous selected seeds
for the contextual-possibilistic rule.
5.3 Iterative Refining Approach
Behavior
In this section, the quality of the refined possibility
distributions is evaluated. Considering the expert
knowledge as being expressed through learning
areas delimitation, i.e. through statistical data, the
obtained results are illustrated in figure 6, where
three possibility distributions (PD) are plotted for
each considered case: the reference (representing all
the class pixels in the image), the initial and the
refined possibility distributions.
A close analysis of the obtained results shows that
the refined possibility distributions fulfil the targeted
objective and converge towards reference possibility
distributions. Possibilistic pixel-based classification,
using the maximum rule, is applied to this synthetic
image in three cases: the first case without possibility
distributions refining, the second case after refined
possibility distributions and the third one is the
optimal case (using the reference possibility
distributions). The calculated classification error rate
in the first case is (20.5%), in the second case is
(17.3%), and in the optimal case is (16.4%). As it is
clear, the classification error rate decreases after the
refining of the possibility distributions.
0 0.1 0.2 0.3 0. 4 0.5 0.6 0.7 0.8 0.9 1
0
2000
4000
6000
8000
10000
12000
possibilistic confidence threshold
correctly selected seeds
erroneously selected seeds
[]
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
2000
4000
6000
8000
10000
12000
possibilistic confidence threshold
correctly selected seeds
erroneous ly selec ted seeds
C
2
Learning zone
C
1
:
G
(m
1
,σ
1
)
C
2
:
G
(m
2
,σ
2
)
0 50 100 150 200 250
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
gray level
possibility
classe1
classe2
C
1
Learning zone
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
180

Figure 6: Initial, refined, and reference possibility
distributions.
5.4 Medical Application
The proposed approach is applied on a set of two
mammographic images composed of two classes
(figure 7) tumor and normal tissue. This set is
extracted from the MIAS image database
(Mammographic Image Analysis Society). In order
to show the performance of the proposed approach,
possibilistic pixel-based classification is applied to
these mammographic images in two cases: the first
case shows classification results according to the
maximum rule, without possibility distributions
refining while the second one gives classification
results through refined possibility distributions.
Figure 7: (a) Set of two mammographic images composed
of two classes, (b) Contour extracted before possibility
refining.distribution refining, (c) Contour extracted after
possibility distribution refining.
A visual analysis of the obtained results shows
that the proposed approach allows better description
of the small details in areas of tumor, so having a
good detection of the region of interest. This is due
to the positive effect resulting from integrating new
possibilistic seeds in the possibility distribution
6 CONCLUSIONS
The proposed approach consists on the use of an
initial knowledge expressed by the expert,
transforming this knowledge into an initial
probability density functions, and then using
Dubois-Prade’s transformation to obtain possibility
distributions. The application of contextual
possibilistic reasoning allows enriching the expert’s
initial knowledge by taking into consideration a lot
of pixels belonging to the class and fulfilling the
conditions during the incremental learning. The
target of the proposed approach is to construct
possibility distribution (to be used for pixel-based
classification purposes) through a statistical iterative
estimator exploiting contextual possibilistic
knowledge.
REFERENCES
Bruzzone, L., Fernàndez P. D., 1999. Incremental-learning
neural network for the classification of remote-sensing
images. Elsevier Science, Pattern Recognition Letters
20, pp.1241-1248.
Dubois, D., Prade, H., 1980.Fuzzy Sets and Systems:
Theory and Applications. Academic Press, New York.
Dubois, D., Prade, H., 1983. Unfair Coins and Necessity
Measures: towards a possibilistic Interpretation of
Histograms. Fuzzy Sets and Syst. Vol.10, pp. 15-20.
Epanechnikov, V.A., 1969. Non-parametric estimation of
a multivariate probability density. Theory of
Probability and its Applications 14: 153–158.
Hüllermeier, E., 2003. Possibilistic Instance-Based
Learning. Fuzzy Set and Possibility Theory-Based
Methods in Artificial Intelligence, vol. 148, pp. 335-
383.
Kikuchi, Sh., Perincherry, V., 2004. Handling Uncertainty
in Large Scale Systems with Certainty and Integrity.
MIT Engineering Systems Symposium, Cambridge.
Mouchaweh, M. S., Devillez, A., Villermain, L. G.,
Billaudel, P., 2002. Incremental learning in Fuzzy
Pattern Matching, Elsevier Science.
Tso, B., and Mather, P. M., 2009. classification methods
for remotely sensed data. taylor & francis group.
Zadeh, L.A., 1978. Fuzzy Sets as a Basis for a Theory of
possibility. Fuzzy Sets Syst., vol. 1, PP.3-28, 1978.
0 50 100 150 200 250
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
gray level
possibility
Initial PD
Refined PD
Refernce PD
(
b
)
(
a
)
(
c
)
T
est
-1
Test-2
IterativePossibilityDistributionsRefininginPixel-basedImagesClassificationFramework
181
