Possibilistic Similarity based Image Classification
B. Alsahwa
1,2
, S. Almouahed
1
, D. Guériot
1,2
and B. Solaiman
1,2
1
Image & Information Processing Dept., Telecom Bretagne, Institut Mines-Télécom, Brest, France
2
Lab-STICC UMR CNRS 3192, Laboratoire en sciences et technologies de l'information, de la communication et de la
connaissance, Institut Mines-Télécom-Télécom Bretagne-UE, Brest, France
Keywords: Possibility Theory, Classification, Contextual Information, a Priori Knowledge, Possibilistic Similarity.
Abstract: In this study, an approach for image classification based on possibilistic similarity is proposed. This
approach, due to the use of possibilistic concepts, enables an important flexibility to integrate both
contextual information and a priori knowledge. Possibility distributions are, first, obtained using a priori
knowledge given in the form of learning areas delimitated by an expert. These areas serve for the estimation
of the probability density functions of different thematic classes. The resulting probability density functions
are then transformed into possibility distributions using Dubois-Prade’s probability-possibility
transformation. Several measures of similarity between classes were tested in order to improve the
discrimination between classes. The classification is then performed based on the principle of possibilistic
similarity. Synthetic and real images are used in order to evaluate the performances of the proposed model.
1 INTRODUCTION
An accurate and reliable image classification is a
crucial task in many applications such as content
based image retrieval, medical and remote-sensing
image analysis and scene interpretation. Several
techniques of image classification are built on a
local approach of the scene to deal with, as opposed
to those built on segmentation or object (Caloz and
Collet, 2001). It is generally accepted that taking
into account the geometric dimension, including the
context or neighbourhood, contributes to the
performance of the classification (Tso and Mather,
2009). Two families of local classification approach
can be encountered in the literature: The first family
uses a thematic classifier working, first, at pixel-
level only, followed by a step of integrating
contextual information (Kim, 1996) and (Shaban and
Dikshit, 2001). This two-step process constitutes
clearly a weakness. Conversely, the other family
simultaneously combines the rules of thematic
similarity and spatial proximity in a single
classification process (Rakotoniaina and Collet,
2010) and (Besag, 1986).
In this paper, pixel-based image classification
systems are considered under the closed world
assumption. Each pixel from the analyzed image, I,
is assumed to belong to one, and only one, thematic
class from an exhaustive set of M predefined and
mutually exclusive classes Ω = {C
1
, C
2
, ..., C
M
}.
Prior knowledge is assumed to be given as a set of
learning areas extracted from the considered image
and characterizing the M considered classes (from
the expert point of view). Using this prior
knowledge, M class probability density functions are
first estimated using the KDE (Kernel Density
Estimation) approach (Epanechnikov, 1969) and
then transformed into M possibility distributions
encoding the “expressed” expert knowledge in a
possibilistic framework. In the same way, assuming
the considered pixel P
0
as being of a “homogeneous
sub-area”, a local possibility distribution 
P0
(x) will
be constructed. This local possibility distribution
stands for the possibility degree to observe the pixel
P
0
in the considered sub-area. The application of
similarity concept on the M possibility distributions
will lead, on one hand, to determine the similarity
function which maximizes the discrimination
between classes, and on the other hand, to enable the
classification of sub-areas represented by local
possibility distributions
The use of possibilistic concepts increases the
capacity as well as the flexibility to deal with
uncertainty as, for most real-world problems, the
modelled knowledge is affected by different forms of
imperfections: imprecision, incompleteness,
ambiguity, etc.
271
Alsahwa B., Almouahed S., Guériot D. and Solaiman B. (2013).
Possibilistic Similarity based Image Classification.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 271-275
DOI: 10.5220/0004265002710275
Copyright
c
 SciTePress

In the next section, a brief review of basic
concepts of possibility theory is introduced. Study of
different similarity functions to quantify the
similarity between classes is the subject of the third
section. The proposed approach will be detailed in
the forth section. Section 5 is devoted to the
experimental results obtained when the proposed
approach is applied using synthetic as well as real
images.
2 POSSIBILITY THEORY
Possibility theory was first introduced by Zadeh in
1978 as an extension of fuzzy sets and fuzzy logic
theory to express the intrinsic fuzziness of natural
languages as well as uncertain information (Zadeh,
1978). In the case where the available knowledge is
ambiguous and encoded as a membership function
into a fuzzy set defined over the decision set, the
possibility theory transforms each membership value
into a possibilistic interval of possibility and
necessity measures (Dubois and Prade, 1980).
2.1 Possibility Distribution
Let us consider an exclusive and exhaustive universe
of discourse Ω = {C
1
, C
2
,..., C
M
} formed by M
elements C
m
, m = 1, ..., M (e.g., thematic classes,
hypothesis, elementary decisions, etc).
Exclusiveness means that one and only one element
may occur at time, whereas, exhaustiveness refers to
the fact that the occurring element certainly belongs
to Ω. A key feature of possibility theory is the
concept of a possibility distribution, denoted by ,
assigning to each element C
m
 a value from a
bounded set [0,1] (or a set of graded values). This
value (C
m
) encodes our state of knowledge, or
belief, about the real world and represents the
possibility degree for C
m
to be the unique occurring
element.
2.2 Possibility Distributions Estimation
based on Pr- Transformation
Two approaches are generally used for the
estimation of a possibility distribution. The first
approach consists on using standard forms
predefined in the framework of fuzzy set theory for
membership functions (i.e. triangular, Gaussian,
trapezoidal, etc.), and tuning the form parameters
using a manual or an automatic tuning method. The
second possibility distributions estimation approach
is based on the use of statistical data where an
uncertainty function (e.g. histogram, probability
distribution function, basic belief function, etc.); is
first estimated and then transformed into a
possibility distribution
As we consider that the available expert’s
knowledge is expressed through the definition of
learning areas representing different thematic
classes, i.e. statistical data, we will focus on the
second estimation approach. Several Pr-
transformations are proposed in the literature.
Dubois et al. (Dubois and Prade, 1983) suggested
that any Pr- transformation of a probability
distribution function, Pr, into a possibility
distribution, , should be guided by the two
following principles:
 The probability-possibility consistency
principle:
() Pr(), AAA


(1)
 The preference preservation principle:
Pr( ) Pr ( ) ( ) ( ), , AB ABAB

   
(2)
Verifying these two principles, a Pr-
transformation has been suggested by Dubois et al.
(Dubois and Prade, 1983):



M
mm j m
j=1
π(C )= (C )= minPr(C ), Pr(C )





(3)
In our study, this transformation is considered in
order to transform the probability distributions into
possibility distributions.
3 SIMILARITY MEASURES
The issue of comparing imperfect pieces of
information depends on the way these pieces of
information are represented. In the case of
possibility theory, comparing uncertain pieces of
information comes down to comparing possibility
distributions representing these pieces of
information.
Considering the expert’s predefined set of M
thematic classes contained in the analyzed image,
={C
1
, C
2
..., C
M
}, a set of M possibility
distributions can be defined as follows:


C
m
C
m
π : 0,1
(P) π ((P))
D
xx


where D refers to the definition domain of the
observed feature x(P). For each class C
m
, 
C
m
(x(P))
associates each pixel PI, observed through a
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
272

feature x(P)D, with a possibility degree of
belonging to the class C
m
, m = 1, ..., M.
Considering two classes C
m
and C
n
of the set ,
different possibilistic similarity and distance
functions “Sim” can be defined between their two
possibility distributions π
Cm
and π
Cn
. The behaviour
of these functions can be studied in order to obtain a
better discrimination between classes C
m
and C
n
. To
do this, calculating a similarity matrix Sim(π
Cm
, π
Cn
)
informs us about such inter-classes behaviour and
will help in choosing the right measure in the given
context:





CC CC
mm mn
CC CC
nm nn
π ,ππ,π
π ,ππ,π
Sim Sim
S=
Sim Sim





(4)
3.1 Possibilistic Similarity Functions
This subsection is devoted to review some existing
possibilistic similarity and distance functions which
are the most frequently encountered in the literature:
- Information closeness: this similarity measure
was proposed by (Higashi and Klir, 1983):
CC CC C
mn mm n
CC C
nm n
(π ,π )=g(π ,ππ) +
g(π ,ππ)
G 

(5)
where g(
C
m
,
C
n
)=U(
C
n
)-U(
C
m
).

is taken as
maximum operator and U is the non-specificity
measure. Given an ordered possibility distribution π
such that 1= π
1
≥ π
2
≥…≥ π
n
the U of π is given by:
n
i
i=1
i+12 12
(π)=[ π )log i]+(1-π )log n(π -U

(6)
where π
n+1
=0 by convention. Hence the similarity
measure based on the Information closeness is given
by:

CC
mn
CC
mn
max
(π ,π )
π ,π 1
Sim
G
G
G

(7)
- Minkowski distance: Since possibility
distributions are often represented as vectors, the
most popular metrics for possibility distributions are
induced by the Minkowski norm (Lp) which is used
in vector spaces.

 
p
p
ii
i=1
pC C C C
mn m n
L π ,π = π x-π x
D

(8)
Three particular cases of equation (10) are often
investigated: L
1
-norm (Manhattan distance), L
2
-
norm (Euclidean distance), and L
∞
-norm (Maximum
distance). These cases of Minkowski distance can be
transformed into similarity measure by the
following:

p
CC
mn
p
p
L
π ,π 1
Sim
D

(9)
- Information affinity: this similarity measure
was proposed by Jenhani et al. (Jenhani et al., 2007)

CC CC
mn mn
CC
mn
κ L(π ,π ) λ Inc(π ,π )
p
π ,π 1
κλ
Sim
IA



(10)
Where κ>0 and λ>0, Inc(
C
m
,
C
n
) represents the
inconsistency degree between 
C
m
and
C
n
defined
as follows
CC C C
mn m n
Inc(π ,π ) 1 max(min(π , π )
(11)
3.2 Evaluation of the Similarity
between Two Classes
A 100×100 synthetic image composed of two
thematic classes is generated in order to evaluate the
similarity between two classes. The intensity of the
pixels from C
1
and C
2
are generated as two Gaussian
distributions G(m
1
=110, σ
1
=10) and G(m
2
=120,
σ
2
=10)(Figure 1)
The evaluation principle of the similarity
between the two classes is to retain the similarity
function whose similarity matrix is the closest to the
identity matrix I
2
in term of Euclidean distance D:
 
,
2
2
D= S i,j -I i,j
ij





(12)
D was calculated for each similarity function by
firstly varying the mean of the class C
2
and then the
standard deviation of class C
2
, while maintaining a
fixed value for the mean and standard deviation of
the class C
1
(Figure 1).
From the curves in Figure 1, the similarity
function called “Maximum distance” Sim
∞
(
C
m
,
C
n
)
tends to the identity matrix faster than the other
functions when the studied values m
2
-m
1
and σ
2
-σ
1
increase.
PossibilisticSimilaritybasedImageClassification
273

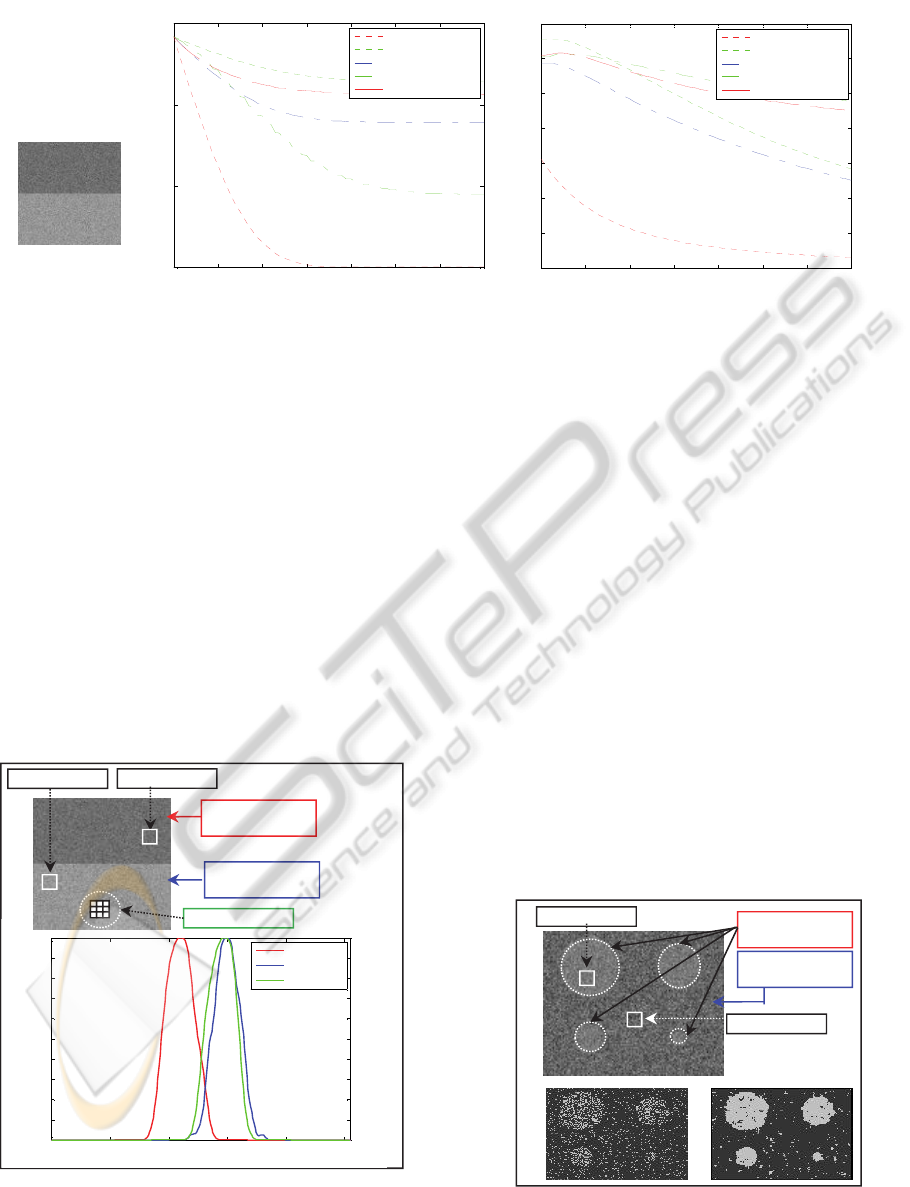
Figure 1: (a) Synthetic image (b) Evolution of the measure D as a function of the mean difference between classes C
1
and
C
2
(c) Evolution of the measure D as a function of the difference of deviations between classes C
1
and C
2
.
4 THE PROPOSED
CLASSIFICATION APPROACH
As previously detailed, the samples initial set,
considered by the expert, is used in order to estimate
the probability density functions of different
thematic classes, which in turns are transformed into
possibility distributions through the application of
the Pr- Dubois-Prade’s transformation.
The estimation of these M possibility
distributions forms the first step in the proposed
approach. The second step consists in the
classification of each pixel of the analyzed image I
by firstly estimating the local possibility distribution
Figure 2: Synthetic image, possibility distributions of
classes C
1
, C
2
and the local possibility distribution in a
subzone around the pixel of interest P
0
.
around the pixel of interest P
0
. Second, the process
of assigning a class to the considered pixel P
0
is to
determine the nearest class via the similarity
function Sim
∞
used to measure the similarity
between this pixel’s local possibility distribution and
possibility distributions of each of the M classes
(Figure 2).
5 EXPERIMENTAL RESULTS
5.1 Simulated Data
For the experimental evaluation purpose, a new
synthetic image of size 96×128 pixel is generated
(Figure 3). Pixels from C
1
and C
2
are generated as
two Gaussian distributions G(m
1
=125, σ
1
=15) and
G(m
2
=100, σ
2
=20). This synthetic image is classified
using the proposed approach and the Bayesian
approach (Hand, 1981), respectively. The
Figure 3: (a) Synthetic image (b) Bayesian classification
(c) Proposed approach classification.
0 10 20 30 40 50 60 70
0
0.5
1
1.5
m
2
-m
1
D
Maximum distance
Manhattan
Euclidean
Information Affinity
Information closeness
0 10 20 30 40 50 60 70
0
0.2
0.4
0.6
0.8
1
1.2
1.4
sigma
2
-sigma
1
D
Maximum distance
Manhattan
Euclidean
Information Affinity
Information closeness
(
b
)
(
c
)
σ
2
=σ
1
=10
m
1
=110,
m
2
=120
(
a
)
0 50 100 150 200 250
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
gray level
possibility
Poss.dist.(C
1
)
Poss.dist.(C
2
)

(P
0
)
Subzone around P
0
C
1
: G
(m
1
,σ
1
)
C
2
: G
(m
2
,σ
2
)
C
1
Learning zone
C
2
Learning zone
C
1
Learning zone
C
2
Learning zone
C
1
: G
(m
1
,
σ
1
)
C
2
: G
(m
2
,
σ
2
)
a
b
c
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
274

classification error rate when using the possibilistic
approach with Sim
∞
function is 8.5% while the error
rate obtained by the Bayesian approach is 18.3%.
5.2 Medical Application
The proposed approach of classification is applied
on a mammographic image composed of two
classes: tumor and normal tissue (figure 4). This
image is extracted from the MIAS image database
(Mammographic Image Analysis Society).
Figure 4: (left) A mammographic image composed of two
classes, (right) Classified image using the proposed
approach.
A visual analysis of the obtained results shows
that the proposed approach allows obtaining an
interesting homogeneity of the regions determined
from samples based on measures limited to windows
of size 3 \times 3.
6 CONCLUSIONS
In this study, a classification approach was
developed based on the possibility theory that
enables the integration of contextual information and
a priori knowledge. Indeed, one of the key points of
the proposed approach is to characterize the pixel to
be classified taking into account its neighbourhood
through the creation of local possibility distribution.
Another key point of our approach is to propose a
classification method based on the similarity
between class possibility distribution and local
possibility distribution, and not on a membership
degree, of parameters extracted from the local
window, to possibility distributions of classes. The
first results on both the synthetic image and the real
medical image (compared to the results obtained
using a Bayesian approach) seem promising.
REFERENCES
Besag, J., 1986. On the statistical analysis of dirty
pictures. Journal of the Royal Society, series B, vol.
48, pp. 259-302.
Caloz, R., and Collet, C., 2001. Précis de télédétection :
Traitements numériques d’images de télédétection.
Presses de l’Université du Québec, Vol.3, 386 p,
Canada.
Dubois, D., Prade, H., 1980.Fuzzy Sets and Systems:
Theory and Applications. Academic Press, New York.
Dubois, D., Prade, H., 1983. Unfair Coins and Necessity
Measures: towards a possibilistic Interpretation of
Histograms. Fuzzy Sets and Syst. Vol.10, pp. 15-20.
Epanechnikov, V. A., 1969. Non-parametric estimation of
a multivariate probability density. Theory of
Probability and its Applications 14: 153–158.
Higashi, M., Klir, G. J., 1983. Measures of uncertainty and
information based on possibility distributions.
International Journal of General Systems, 9 (1), 43-
58.
Hand, D. J., 1981. Discrimination and Classification.
Wiley Series in Probability and Mathematical
Statistics.
Jenhani, I., Ben Amor, N., Elouedi, Z., Benferhat, S.,
Mellouli, K., 2007. Information affinity: A new
similarity measure for possibilistic uncertain
information. In Proceedings of the 9th European
Conference on Symbolic and Quantitative Approaches
to Reasoning with Uncertainty, 840-852.
Kim, K. E., 1996. Adaptive majority filtering for
contextual classification of remote sensing data.
international journal of remote sensing, Vol. 17, pp.
1083-1087.
Rakotoniaina, S.,and Collet, C., 2010. Amélioration de la
Qualité de la Classification d’une Image
Multispectrale à l’aide d’un classificateur contextuel,
Revue Télédétection, Vol. 9, pp. 259-27.
Shaban, M.A., and Dikshit, O.,2001. Improvement of
classification in urban areas by the use of textural
features : the case of Lucknow city, Uttar Pradesh,
International Journal of Remote Sensing, vol. 22, pp.
565-593.
Tso, B., and Mather, P. M., 2009. classification methods
for remotely sensed data. taylor & francis group.
Zadeh, L. A., 1978. Fuzzy Sets as a Basis for a Theory of
possibility. Fuzzy Sets Syst., vol. 1, PP.3-28, 1978.
Tumo
r
Normal
tissue
PossibilisticSimilaritybasedImageClassification
275