Droplet Tracking from Unsynchronized Cameras

L. A. Zarrabeitia, F. Z. Qureshi and D. A. Aruliah

Faculty of Science, University of Ontario Institute of Technology, Oshawa, ON, Canada

Keywords:

Stereo Reconstruction, Multi-view Geometry, Nonlinear Motion, Blood Flight, Parameter Estimation.

Abstract:

We develop a method for reconstructing the three-dimensional (3D) trajectories of droplets in ﬂight captured

by multiple unsynchronized cameras. Triangulation techniques that underpin most stereo reconstruction meth-

ods do not apply in this context as the image streams recorded by different cameras are not synchronized. We

assume instead a priori knowledge about the motion of the droplets to reconstruct their 3D trajectories given

unlabelled two-dimensional tracks in videos recorded by different cameras. Our approach also avoids the chal-

lenge of accurately matching droplet tracks across multiple video frames. We evaluate the proposed method

using both synthetic and real data.

1 INTRODUCTION AND

BACKGROUND

Recovering the three-dimensional structure of a scene

requires a system that can match features extracted

from at least two distinct images captured by cam-

eras at different spatial locations; once features are

matched, reconstruction proceeds using triangula-

tion (Hartley and Zisserman, 2004). A single monoc-

ular image is insufﬁcient for scene reconstruction un-

less some a priori information regarding scene geom-

etry is available. When targets in the scene are mov-

ing, the videos captured by the cameras must also be

synchronized.

The paper (Zarrabeitia et al., 2012) summarizes

a method for tracking droplets in ﬂight ﬁlmed by a

stereo camera pair. The videos consist of experimen-

tal simulations of blood-spattering events (a projec-

tile hitting simulated ﬂesh scattering blood droplets

through a scene). Following background removal

and segmentation of droplets in each video frame,

each individual foreground blob is tracked across a

sequence of video frames according to a polyno-

mial least-squares model that locally approximates

the projection of the global trajectory into each im-

age. This model-based tracking is designed to deal

gracefully with the similarity of droplets in shape,

size, and color, with the lack of feature points on in-

dividual droplets, and, most importantly, with incom-

plete droplet paths. Even though the cameras are syn-

chronized in this set of experiments, droplet positions

are available in every frame due to occlusions, noise,

or droplets exiting the view of one—but not both—

cameras. In fact, many targets segmented from one

camera’s video do not correspond to suitable matches

in the other’s due to false positives and false negatives

during background subtraction and 2D tracking.

The 3D trajectories extracted by the methods

in (Zarrabeitia et al., 2012) correspond to the sub-

set of 2D image trajectories as reconstructed from

each camera’s respective videos for which a match

could be found. The work in (Murray, 2012) uses

those 3D trajectories to estimate physical parameters

in an ordinary differential equation (ODE) model as-

sociated with each droplet tracked. In the present

paper, we demonstrate that the accuracy of ODE-

based motion estimation increases signiﬁcantly with

the number of measurements, so it is desirable to

maximize the number of available data points. The

unmatched points discarded in the reconstruction al-

gorithm of (Zarrabeitia et al., 2012), then, constitute

an unexploited potential source of information.

There is a strategy to estimate the 3D world co-

ordinates of a target captured by one camera but not

the other. The method of (Park et al., 2010) provides

a means to extract motion parameters from a set of

monocular images. Unfortunately, this approach re-

lies on approximating the motion model by a linear

combination of basis functions speciﬁed a priori. A

nonlinear ODE motion model as in (Murray, 2012)

involves the solution of an IVP (initial-value prob-

lem); this approach captures motions that cannot be

easily modelled by linear models. It does rely on ro-

bust IVP solvers which, fortunately, are mature and

widely available.

459

A. Zarrabeitia L., Z. Qureshi F. and A. Aruliah D. (2013).

Droplet Tracking from Unsynchronized Cameras.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 459-466

DOI: 10.5220/0004265104590466

 SciTePress

Thus, we propose a method to relax the require-

ment of synchronized cameras for trajectory recon-

struction in scenes with moving targets where non-

linear ODE motion models are appropriate. This ap-

proach is necessary in realistic tracking scenarios; for

instance, a feature might be occluded (or move out of

the frame or be lost due to noise) for a few frames in

the view of some cameras but while still being visi-

ble to others. Our approach does require an a priori

model of object motion; in particular, we assume that

each object in the scene moves according to an ODE

model described by some set of physical parameters.

With reasonable estimates of those physical param-

eters, it is possible to reconstruct the motion of ob-

jects not just between successive frames but through-

out a longer time interval. Moreover, even when si-

multaneous measurements are available, if the ODE

model faithfully describes the motion, our reconstruc-

tion based on estimating the motion parameters can

provide better three-dimensional reconstructions than

those produced by triangulation alone. We highlight

the fact that our technique retrieves the physical mo-

tion parameters without explicitly computing the spa-

tial locations of the target. As such, we can avoid bias

caused by errors in 3D reconstruction.

The present paper builds on techniques in (Mur-

ray, 2012) and in (Park et al., 2010). First, we general-

ize the extraction of motion parameters from monoc-

ular images from the linear to the nonlinear case. Sec-

ond, we use a nonlinear ODE model to estimate phys-

ical motion parameters and the 3D world coordinates

of droplets simultaneously. Our generalization loses

the elegance and computational efﬁciency of Park’s

work but is more appropriate in scenarios where non-

linear ODE models apply. We compare four dif-

ferent motion models: two are ODE-based two are

polynomial-based (speciﬁcally quadratic polynomi-

als). The accuracy of each model is assessed using

synthetic data and real data (as obtained from the

video experiments in (Zarrabeitia et al., 2012)).

2 3D RECONSTRUCTION FROM

SYNCHRONIZED CAMERAS

Let us consider the problem of 3D reconstruction us-

ing n synchronized pinhole cameras. Each camera i

is described by its 3 × 4 projection matrix P

, where

i ∈ [1,n]. For each camera we also deﬁne a projec-

tion operator ϕ

: R

→ R

that maps R

to the image

plane. Then P

and ϕ

are related by the following

equation:



(λ

λ)



s = P





, (1)

where λ

λ ∈ R

is a 3D point not lying on the plane

parallel to the image plane and passing through the

center of projection.

Now consider a set of simultaneous measurements

M = {hx

i}, representing the image coordinates

of an object at location λ

λ = λ

λ(t

) when viewed by

camera i with projection matrix P

. Generally speak-

ing, x

is a noisy estimate of ϕ

(λ

λ) due to sensing lim-

itations of physical cameras, such as occlusions, and

inaccuracies present in detection routines. This sug-

gests that the reconstruction problem consists of ﬁnd-

ing the location λ

λ that best explains the observations

. We can formalize this notion by introducing an er-

ror function e(λ

λ,M), minimizing which will yield the

location λ

λ that best explains the observations. One

such error function is deﬁned by the Euclidean dis-

tance between the observations and the expected lo-

cations of the projections given the operators ϕ

e(λ

λ,M) =

∑

− ϕ

(λ

λ)k

. (2)

It is straightforward to minimize the above error

function by solving the following least squares prob-

lem

λ = min

∑

− ϕ

(λ

λ)k

. (3)

It is worth remembering that the error measure (2)

is biased if the aspect ratio of a camera is not 1. This,

however, can be easily remedied when internal cam-

era parameters are known. The projection operators

are nonlinear (1) and so the least squares problem

described by (3) is also nonlinear. We can derive a

linear approximation to this least squares problem by

observing that vectors



(λ

λ)



and P





differ only by a scaling factor, suggesting that their

cross product is 0:









= 0 (4)





i,1:3

λ = −





i,4

(5)

λ = q

, (6)

where [·]

is the skew-symmetric representation of

the cross product (Hartley and Zisserman, 2004). The

third equation of (5) is a linear combination of the

previous two, so it can be safely discarded. The ma-

trix Q

and the vector q

in (6) span only the ﬁrst two

equations of (5).

If two or more measurements at time t are avail-

able, the 3D location of the object can be retrieved by

solving the linear least squares problem

)λ

λ = (q

) (7)

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

460

over the measurements recorded at time t. The so-

lutions of (3) and (7) do not necessarily agree if the

measurements are noisy. Speciﬁcally, the error asso-

ciated with (3) is related to the distance between the

projections of the guessed 3D location and the obser-

vations in the image plane; whereas, the error in (4)

depends upon both the sine of the angle between vec-

tors





and P





and their lengths.

3 LINEAR RECONSTRUCTION

OF 3D MOTION FROM

UNSYNCHRONIZED CAMERAS

Equations (3) and (7) require at least two simultane-

ous measurements of the target in order to reconstruct

its 3D location. In a stereo system, for example, at

most two measurements are available for a given tar-

get. If one of the measurements is unavailable (due

to, say, occlusion) or otherwise corrupted (due to a

misdetection or misclassiﬁcation) the 3D location of

the target cannot be estimated. In most cases it is not

even possible to determine which one of the two ob-

servations is corrupted.

If, however, we are given a motion model for a tar-

get, it is sometimes possible to estimate the location

of the target even when two simultaneous measure-

ments are not available. (Park et al., 2010) explores

this idea by assuming that the target’s motion can be

approximated by a linear combination of basis func-

tions Θ = (θ

,. ..,θ

); in particular,

= λ

λ(t) ≈

∑

j=1

(t) = Θ

C (8)

for some coefﬁcients C = (c

,. ..,c

)

∈ R

. Using

the linearization (6), we can then ﬁnd the parameters

C by solving the linear least squares problem

ΘC = q, (9)

where

Q =







0 .. . 0

0 Q

.. . 0

0 0 .. . Q







Θ =













and q =













4 NONLINEAR

RECONSTRUCTION OF 3D

MOTION FROM

UNSYNCHRONIZED CAMERAS

Equation (9) is easy to set up and fast to solve. How-

ever, it is limited to motion models that can be ap-

proximated by a linear combination of a ﬁnite set of

basis functions Θ. If the subspace hΘi does not con-

tain a reasonable approximation of the motion model

for the target in question, solving Equation (9) yields

an erroneous reconstruction. Furthermore, the error

measure obtained from (7) is generally different from

that of (2). These observations suggest, ﬁrstly, that it

is possible to estimate the 3D trajectory of a target

(given its motion model) from multiple unsynchro-

nized multi-view image measurements and, secondly,

that we need to minimize the error (2) directly.

Let L

(t) be a function that describes the loca-

tion of the target at time t. L

(t) is parametrized by

α ∈ R

and we assume that α

α is not known. Given

the set of observations M = {hx

i} and a set of

parameters α

α, the discrepancy between the model L

and the observations M is given by

(α

α,M) =

∑

i∈M

− ϕ

. (10)

The optimal set of parameters

α can be found by min-

imizing the error e

(α

α,M):

α = min

∑

i∈M

− ϕ

))k

. (11)

Notice that L

is a generalization of (8) so we can

use (11) to ﬁnd the parameters C by minimizing the

error measure (2). In this case, we can use the solution

C of (9) as the initial guess for (11). This strategy

can be generalized for any motion model whenever an

initial guess α

α can be inferred from the coefﬁcients of

some linear approximation.

5 SYNTHETIC EXPERIMENT

RESULTS

We simulate the motion of an spherical object mov-

ing under the effects of drag and gravity after an ini-

tial impact. This motion is given by the differential

equation (Murray, 2012)

v = −

κρ

kvkv

rρ

− g (12)

where κ represents the drag coefﬁcient, r is the ra-

dius, ρ

and ρ

are respectively the densities of the

DropletTrackingfromUnsynchronizedCameras

461

Table 1: Initial values for the synthetic experiments (Ray-

mond et al., 1996).

Variable Range Description

g (0,9.80665,0)

m/s

Acceleration due to gravity

1m/s ≤ kv

k ≤ 10 m/s Initial velocity vector

r 1mm ≤ r ≤ 4mm Sphere radius

1.1839 kg/m

Air density at 25

◦

1062 kg/m

Density of porcine blood

1.8616 × 10

−5

N · s/m

Dynamic viscosity of air at 25

◦

ﬂuid and the object, g is the gravitational acceleration

vector and v is the velocity vector.

The drag coefﬁcient κ is computed from the

Reynolds number Re, which depends on the velocity

v, the radius r, the density of the ﬂuid ρ

and the vis-

cosity of the ﬂuid µ

(Murray, 2012; Aggarwal and

Peng, 1995; Liu et al., 1993; Peng and Aggarwal,

1996):

κ =







(1 +

) if Re ≤ 1000

0.424 otherwise

(13)

Re =

2ρ

kvkr

(14)

A synthetic experiment consists of generating a

trajectory using equation (12) for some randomly se-

lected initial values of position, velocity and radius

and project them into two pre-selected cameras. The

values are chosen according to Table 1.

5.1 Simpliﬁed Flight Models

We attempt to ﬁnd the ﬂight parameters correspond-

ing to each of the projected trajectories under different

ﬂight assumptions. We consider four ﬂight models:

1. Murray’s model. L

corresponds to the solution

of equation (12), α

α = (λ

,r) ∈ R

2. Quadratic drag. From the well-known quadratic

drag equation and Newton’s second law of mo-

tion, we can derive:

v = −Kkvkv − g, α

α = (λ

,K) ∈ R

(15)

We can also derive this model from equation (12)

by assuming a constant drag coefﬁcient κ.

3. No drag. If we ignore the effects of drag and only

consider gravity, the motion of the a droplet is de-

scribed by:

(t) = λ

t +

, α

α = (λ

) ∈ R

(16)

4. Quadratic polynomial. A trivial generalization of

the no drag model is to approximate the ﬂight

with a quadratic polynomial. This model corre-

sponds to the unrealistic scenario of the drag force

being unknown but constant, in both direction and

magnitude:

(t) = λ

+ v

t + at

, α

α = (λ

,a) ∈ R

(17)

Murray’s model has 7 degrees of freedom, cor-

responding to the initial position λ

∈ R

, velocity

∈ R

and radius r ∈ R

. Similarly, the quadratic

drag model also has 7 degrees of freedom, counting

the constant drag coefﬁcient K. The two polynomial

models have respectively 6 and 9 degrees of free-

dom, corresponding to the non-ﬁxed coefﬁcients of

the polynomials (λ

,a ∈ R

Our goal is to evaluate whether equation (11) is

able to retrieve the ﬂight parameters of each synthetic

experiment, or at least a set of parameters that explain

the observations from the synthetic cameras, as well

as to evaluate the ability of the simpliﬁed ﬂight mod-

els to explain the observations.

For each experiment, we solve (11) using the

Levenberg-Marquardt algorithm. The IVPs (12) and

(15) are solved numerically using the LSODA rou-

tine, which features support for stiff problems such as

these. The initial guesses for λ

and v

are obtained

by solving the linear problem (9) with the set of basis

functions Θ corresponding to the quadratic polyno-

mial ﬂight model:





0 0 t 0 0 1 0 0

0 t

0 0 t 0 0 1 0

0 0 t

0 0 t 0 0 1





5.2 Parameter Retrieval

The ﬁrst synthetic experiment attempts to establish

the accuracy of the parameter retrieval using equation

(11). To this end, we generate a set of trajectories us-

ing some random values of initial position, velocity

and radius. These trajectories are then projected into

two virtual cameras to obtain one set of measurements

M per trajectory. To simulate misdetections and non-

synchronization, some measurements are randomly

eliminated. We then proceed to solve the optimiza-

tion problem (11) and compare the resulting parame-

ters with the known ground truth.

Table 2 shows the result with 100 trajectories,

each evolved for 0.5 seconds at a simulated framerate

of 1300 frames per second. Each row summarizes the

results after randomly eliminating some of the mea-

surements. For each row, we list the probability of

not removing a measurement, the average number of

measurements per path, the mean error in the estima-

tion of the initial location λ

, velocity v

and radius r,

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

462

Table 2: Accuracy of the estimated parameters from noiseless data, compared with the ground truth. The errors are given in

terms of the average distance between the estimated parameters and the true parameters, the average error displays the mean

distance between the reconstructed trajectory and the ground truth.

Probability

of keeping a

measurement

Avg. measure-

ments per path

error (cm) v

error, (m/s) radius error (mm) Avg. error (m)

0.5 653.16 1.11e-04 4.30e-06 3.45e-06 1.2e-06

0.1 131.08 2.54e-04 1.13e-05 9.85e-05 3.2e-06

0.05 66.15 1.09e-05 1.82e-06 8.81e-05 8.0e-07

Table 3: Like table 2, but with normal noise of σ = 5 added to the measurements.

Probability

of keeping a

measurement

Avg. measure-

ments per path

error (cm) v

error, (m/s) radius error (mm) Avg. error (m)

0.5 651.73 4.19e+00 1.71e-01 2.35e-01 5.1e-02

0.1 129.43 8.93e+00 3.67e-01 4.22e-01 1.1e-01

0.05 66.98 1.08e+01 4.09e-01 5.52e-01 1.3e-01

Figure 1: Reprojection into the two virtual cameras of some

of the trajectories used in Table 3. The dotted line repre-

sents the noisy data, the solid line is the ground truth, and

the dashed line shows the trajectory reconstructed from the

noisy data.

and the mean distance between the reconstruction and

the ground truth trajectory. In Table 3, normal noise

with σ = 5 was added to the measurements. Figure

1 shows the reconstruction for some of the noisy tra-

jectories from 5% of the measurements. Even with so

few points, the reconstructed trajectory is remarkably

similar to the ground truth functions.

5.3 Trajectory Reconstruction and

Extrapolation

In (Zarrabeitia et al., 2012), a 2D quadratic poly-

nomial approximation was employed to track blood

droplets in the image plane. It was found that the

quadratic model was able to accurately predict the ex-

pected locations of the droplets within a very small

time window. It was also noticed that the quadratic

predictions broke down quickly after a few frames

without a measurement, or if too many measurements

were used to estimate the model.

Table 4 compares the accuracy of the reconstruc-

tion if only a small window of time is available. The

accuracy is measured as the average deviation from

the ground truth for the entire simulation time. This

allows us to evaluate the predictive capacity of each

simpliﬁed ﬂight model, that is, how precisely each

model allows us to extrapolate from a small set of

measurements. We can see that the ODE models be-

haved signiﬁcantly better than quadratic polynomial

model. The no drag model also behaved signiﬁcantly

better than the quadratic polynomial model in the

noisy case for the ﬁrst two columns. Figure 2 sug-

gests why this happens: having more degrees of free-

dom, the quadratic polynomial model may overﬁt the

noise in the data, resulting in a very inaccurate extrap-

olation. This is consistent with the prediction break-

down observed in (Zarrabeitia et al., 2012). Without

noise (Figure 3), both ODEs were able to accurately

reconstruct the entire trajectory using only the ﬁrst

0.1s of ﬂight. The polynomial models also behaved

much better with noiseless data, but they were still

signiﬁcantly worse than the ODEs.

6 AN APPLICATION TO THE

BLOOD TRAJECTORY

RECONSTRUCTION PROBLEM

Our main reason for developing the nonlinear recon-

struction method (11) was the study of the motion pa-

rameters of blood droplets. Particularly, we wish to

DropletTrackingfromUnsynchronizedCameras

463

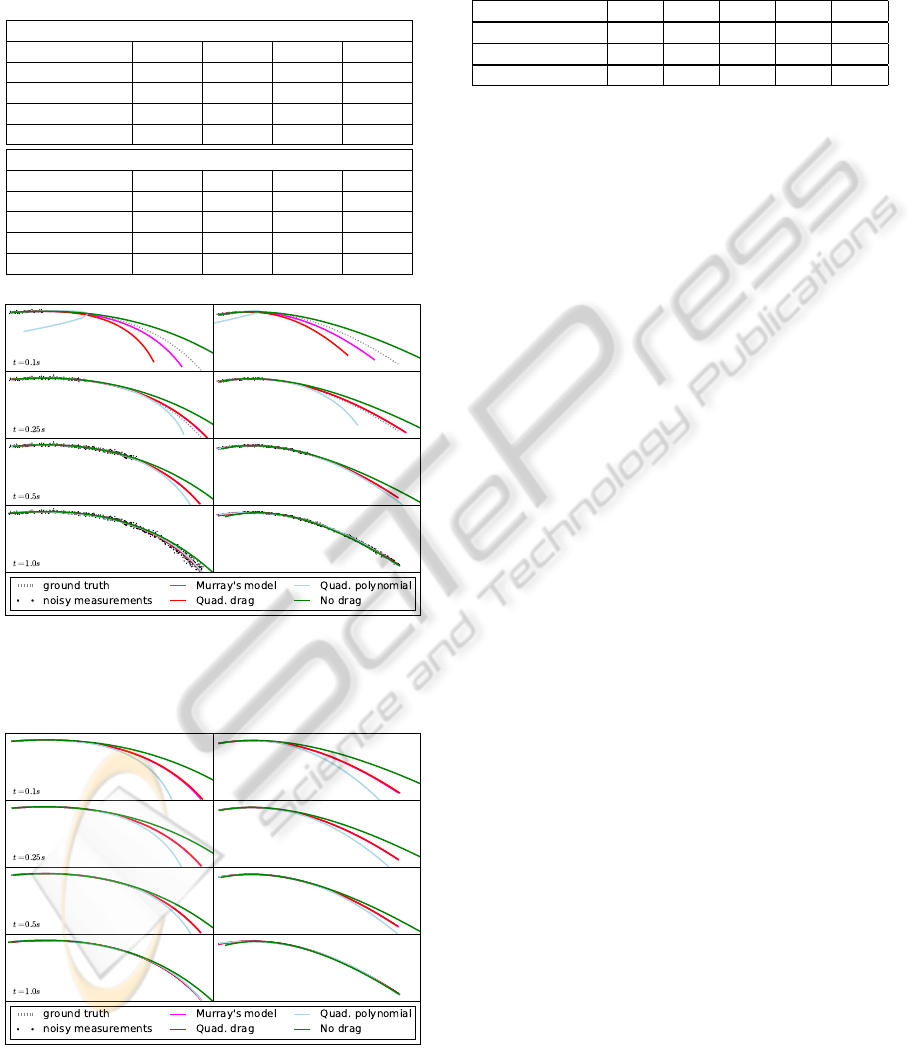
Table 4: Prediction accuracy, with noise (top) and without

noise (bottom). The values represent the mean distance, in

meters, between the ground truth and the estimated model

over the entire trajectory, when only measurements corre-

sponding to the ﬁrst 0.1s, 0.25s,0.5s and 1.0s of ﬂight are

used.

With noise

time (s) 0.1 0.25 0.5 1.0

Murray’s model 0.0041 0.00083 0.00022 9.9e-05

Quad. drag 0.005 0.00096 0.00024 9.9e-05

Quad. polynomial 0.12 0.0075 0.0011 0.00046

No drag 0.0048 0.0027 0.0032 0.0041

Without noise

time (s) 0.1 0.25 0.5 1.0

Murray’s model 1e-05 1e-05 1e-05 1e-05

Quad. drag 7.9e-05 5.6e-05 2.6e-05 1.3e-05

Quad. polynomial 0.00086 0.00071 0.0005 0.00032

No drag 0.0018 0.0019 0.0023 0.0029

Figure 2: Reconstruction of a trajectory from a small

amount of noisy data (σ = 5). Note how, in the ﬁrst row,

the quadratic polynomial model overﬁts the available data,

causing it to behave extremely badly outside of the interval.

Figure 3: Like Figure 2, but without any noise added to the

data.

construct a framework to validate whether (12) is a

Table 5: Average deviation from the ground truth, in cm,

using different reconstructions from noisy data, with detec-

tion accuracy of 0.1, 0.25, 0.5, 0.75 and 1.0. 50 random

trajectories of 1s duration with normal noise (σ = 5) were

used.

Method \ Accuracy 0.1 0.25 0.5 0.75 1.0

Triangulation 33.87 34.78 34.39 34.58 34.22

3D optimization 61.63 11.02 3.192 2.154 1.324

Unsynchronized 5.165 2.961 2.015 1.504 1.285

good approximation, and whether simpler approxima-

tions are suitable under some constraints. An exper-

imental apparatus to measure blood droplet trajecto-

ries is described in (Zarrabeitia et al., 2012; Murray,

2012). Furthermore, (Murray, 2012) used these tra-

jectories to develop and validate (12). However, as

tables 3 and 4 show, the accuracy of the reconstruc-

tion from noisy data depends greatly on the number

of measurements available. It is thus essential to max-

imize the number of useful measurements.

The approach in (Zarrabeitia et al., 2012) is only

able to retrieve 3D coordinates for simultaneous mea-

surements. Due to the noise and random misdetec-

tions, even perfectly synchronized cameras cannot

guarantee ﬁnding a pairing for most of the trajectory.

Moreover, the sensitivity of the stereo reconstruction

with respect to the measurements in the image plane

increases with the distance of the target to the camera

center. Conversely, this means that there is a region

around each reconstructed point that produces very

similar measurements, and the size of this region in-

creases with the depth of the target. Fitting a model to

these reconstructions ignores that they are not equally

accurate.

Table 5 illustrates this issue. The synchronized

reconstruction (triangulation) solves the location of

each point independently, using equation (7). Observe

the very high average deviation from the ground truth.

The 3D optimization consists of ﬁtting the model (12)

to the synchronized 3D reconstruction. It produces a

signiﬁcant improvement over equation (7), though it

still depends heavily on the accuracy of the detector.

Finally, the unsynchronized reconstruction proposed

in this paper, using Murray’s model (12) produces a

signiﬁcantly better approximation to the ground truth.

Ground truth is not available with real trajectories,

such as those measured by (Zarrabeitia et al., 2012)

(Figure 4). This makes it impossible to directly evalu-

ate the reconstruction accuracy. Instead, we can eval-

uate the prediction accuracy of the models. Figure 5

illustrates the reconstruction of a path from real mea-

surements obtained in (Zarrabeitia et al., 2012). The

droplet was recorded for about 0.5s, one of the longest

trajectories in that experiment. This makes it ideal for

evaluating the predictive power of the model, by ﬁt-

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

464

Figure 4: 2D trajectories measured by (Zarrabeitia et al., 2012).

Figure 5: Reconstruction of a real trajectory. Note that, con-

sidering only the ﬁrst 0.1s of ﬂight (top), the ODE models

were a near perfect ﬁt for the overall trajectory, while the

quadratic polynomial model behaved badly. Also note that

because the noise is signiﬁcantly lower than that of ﬁgure 2,

the reconstructions with t = 0.15 are nearly indistinguish-

able.

ting only a small window of time and comparing the

predictions with the actual measurements. The ﬁgure

shows that even with very few data points, the ODE

models were able to accurately predict the entire tra-

jectory.

A more complete test is summarized in Table 6.

This test was run over all the trajectories with at least

100 measurements per camera captured during a sin-

gle experiment. The errors shown are the average of

the distances, in pixels, between the predictions and

the measurements in the image plane. With incom-

plete data, the ODE models behaved signiﬁcantly bet-

ter than the polynomials.

6.1 A Note about Outliers

When dealing with a real detector, such as the one

described in (Zarrabeitia et al., 2012), outliers are

likely to occur. In particular, the parabolic tracker

from (Zarrabeitia et al., 2012) tends to produce out-

Table 6: Prediction accuracy for real paths. Because ground

truth is not available, the errors are given in terms of pixels

in the image plane.

Model \ time (s) 0.1 0.15 0.5

Murray’s model 0.058 0.042 0.016

Quad. drag 0.12 0.048 0.013

Quad. polynomial 0.75 0.2 0.013

No drag 1.4 0.082 0.03

liers at the beginning of the trajectories, when there

is not enough data to ﬁnd the quadratic coefﬁcients.

Outliers may also appear near the end of the trajec-

tory, when the tracker, unable to ﬁnd a new mea-

surement, may consume instead some blob near the

expected location. Most notably, the this also oc-

curs when the liquid droplet impacts a surface, as the

tracker may try to follow the bouncing particles be-

fore giving up (Figure 6, top left).

Both the linear approach (9) and the nonlinear (11)

are sensitive to outliers. In the linear case, they can be

handled with RANSAC, as we only need to solve a

small system of equations for each guess. However,

because our use of (9) is limited to computing a rough

initial guess for the Levenberg-Marquardt iteration,

we don’t need to ﬁlter out the outliers at this stage.

For the nonlinear case, RANSAC is prohibitively

expensive, as it would require to solve a nonlinear op-

timization problem with a differential equation as the

target function, for each candidate subset. Instead, we

follow a 2-pass approach (Figure 6): we use a robust

loss function, such as Huber loss, rewriting (11) as

α = min

∑

i∈M

− ϕ

))) (18)

(x) =



if |x| < δ

δ(|x| −

) otherwise.

(19)

to ﬁnd the outliers (top), followed by another opti-

mization pass with square loss, considering only the

inliers and using the solution of (18) as the initial

guess (bottom).

DropletTrackingfromUnsynchronizedCameras

465

Figure 6: Outlier detection. A ﬁrst pass ﬁts the ODE pa-

rameters using a robustiﬁed loss function (top). The outliers

are then discarded and a second pass computes the ﬁnal ﬁt

(bottom). The original data is represented in red, the ODE

solution is overlaid in black.

7 CONCLUSIONS

We propose a method capable of estimating the 3D

path of a particle from a set of unsynchronized multi-

view image measurements. Our method is able to reli-

ably reconstruct the 3D trajectory of a particle—given

a parametrized model L

(t) describing its motion—

even in the presence of occlusions, misdetections and

misclassiﬁcations. Unlike other attempts that rely

upon motion models to improve 3D estimation accu-

racy, the proposed method makes no linearity assump-

tions about the motion model.

We applied the proposed method to the problem

of estimating the 3D trajectories of blood droplets

as they move through the air under the inﬂuence of

drag and gravity. Physical experiments that were car-

ried out to record these blood droplets are described

elsewhere (Zarrabeitia et al., 2012). We also gen-

erated synthetic dataset that faithfully mimics those

captured from the physical experimental setup men-

tioned above. The synthetic dataset allowed us to

evaluate the proposed approach under controlled set-

tings. We compared the four motion models described

in the previous section and we found that the polyno-

mial motion models fair poorly at the task of extrapo-

lation, i.e., estimating the full 3D trajectory of a par-

ticle given a small set of initial measurements. ODE

based motion models, on the other hand, correctly ex-

trapolated the 3D trajectory of a particle even in the

presence of noisy measurements. We achieved simi-

lar results for the real dataset.

Our results summarized in Table 5 are both ex-

citing and encouraging. We conclude that 3D recon-

struction via triangulation (using synchronized mea-

surements) often exaggerates measurement errors, af-

fecting 3D trajectory estimation. The proposed tech-

nique side-steps this issue by solving for both the 3D

trajectory of a particle and its motion model concomi-

tantly. We show that the proposed method outper-

forms the traditional triangulation based 3D trajectory

reconstruction approach.

REFERENCES

Aggarwal, S. and Peng, F. (1995). A review of droplet

dynamics and vaporization modeling for engineering

calculations. Journal of engineering for gas turbines

and power, 117(3):453–461.

Hartley, R. and Zisserman, A. (2004). Multiple view geom-

etry in computer vision. Cambridge University Press,

edition.

Liu, A. B., Mather, D., and Reitz, R. D. (1993). Modeling

the effects of drop drag and breakup on fuel sprays.

NASA STI/Recon Technical Report N, 93:29388.

Murray, R. (2012). Computational and laboratory investi-

gations of a model of blood droplet ﬂight for forensic

analysis. Master’s thesis, University of Ontario Insti-

tute of Technology.

Park, H., Shiratori, T., Matthews, I., and Sheikh, Y. (2010).

3d reconstruction of a moving point from a series of

2d projections. Computer Vision–ECCV 2010, pages

158–171.

Peng, F. and Aggarwal, S. K. (1996). Droplet motion un-

der the inﬂuence of ﬂow, nonuniformity and relative

acceleration. Atomization and Sprays, Vol. 6:42–65.

Raymond, M. A., Smith, E. R., and Liesegang, J. (1996).

The physical properties of blood—forensic consider-

ations. Science & Justice: journal of the Forensic Sci-

ence Society, 36(3):153–160.

Zarrabeitia, L. A., Aruliah, D. A., and Qureshi, F. Z.

(2012). Extraction of blood droplet ﬂight trajectories

from videos for forensic analysis. In ICPRAM 2012

- Proceedings of the 1st International Conference on

Pattern Recognition Applications and Methods, vol-

ume 2, pages 142–153. SciTePress.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

466