
Multistage Naive Bayes Classifier with Reject Option for
Multiresolution Signal Representation
Urszula Libal
Institute of Computer Engineering, Control and Robotics, Wroclaw University of Technology, Wroclaw, Poland
Keywords: Multistage Classifier, Naive Bayes, Reject Option, Pattern Recognition, Wavelet, Resolution.
Abstract: In the article, two approaches to pattern recognition of signals are compared: a direct and a multistage. It is
assumed that there are two generic patterns of signals, i.e. a two-class problem is considered. The direct
method classifies signal in one step. The multistage method uses a multiresolution representation of signal
in wavelet bases, starting from a coarse resolution at the first stage to a more detailed resolutions at the next
stages. After a signal is assigned to a class, the posterior probability for this class is counted and compared
with a fixed level. If the probability is higher than this level, the algorithm stops. Otherwise the signal is
rejected and on the next stage the classification procedure is repeated for a higher resolution of signal. The
posterior probability is calculated again. The algorithm stops when the probability is higher than a fixed
level and a signal is finally assigned to a class. The wavelet filtration of signal is used for feature selection
and acts as a magnifier. If the posterior probability of recognition is low on some stage, the number of
features on the next stage is increased by taking a better resolution. The experiments are performed for three
local decision rules: naive Bayes, linear and quadratic discriminant analysis.
1 INTRODUCTION
Sometimes the direct approach to classification does
not give the desired results. Then a classifier with
reject option (
Devroye et al., 1996) may be used. The
object rejection is a cancellation of the object
assignment to one of the classes, if the decision is
not certain on a reasonable level. This approach can
reduce the risk of misclassification (Pudil et al.,
1992).
In opposition to a multistage classifier based on
decision trees (Burduk and Kurzyński, 2006);
(Kurzyński, 1988); (Libal, 2010), the new multistage
approach to classification is presented in this article.
There is proposed a multistage classifier, which is a
sequence of Bayes decision rules with the reject
option. The new classifier is dedicated to signal
recognition and uses wavelet representation of
signals. There are assumed only two classes of
signals. In case of inability to identify the class at
some stage (i.e. signal rejection), it will try to
classify the signal to one of the two classes at the
next stage. It should be noted that at each stage there
are still the same two classes considered, and the
number of steps of the algorithm is not determined
arbitrarily.
To avoid the curse of dimensionality (the empty
space phenomenon), the signal is represented by the
wavelet approximation coefficients in the following
way: at an early stage classifier uses signal
representation in a low resolution. And if it is not
enough (i.e. rejection case), then classifier will use
signal representation in an increased resolution at
the next stage. The method of obtaining wavelet
coefficient vectors
,
,…,
by the wavelet
decomposition of signals with the use of the Mallat
algorithm is described in the section 2.1.
2 MULTISTAGE CLASSIFIER
The considered problem is to classify a noised signal
to one of two classes. There is shown a multistage
algorithm with reject option, i.e. on every stage a
local classifier assigns an analysed signal to a class
from 1,2 or rejects it. If the signal was assigned to
class 1 or 2, then algorithm stops. On the other hand,
after the rejection signal stays unclassified and waits
for the classification on the next stage. The
difference between stages is a representation of the
289
Libal U..
Multistage Naive Bayes Classifier with Reject Option for Multiresolution Signal Representation.
DOI: 10.5220/0004266002890292
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2013), pages 289-292
ISBN: 978-989-8565-41-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

signal:
1)
- at the first stage a coarse signal
representation in wavelet bases is
considered (with a small number of wavelet
approximation coefficients for a low
resolution),
2)
- at the second stage and so on,
⋮
m)
- till a detailed representation in a high
resolution (with a large number of coefficients).
2.1 Signal Representation
A multiresolution signal representation, in the form
of the sequence
,
,…,
, can be obtained
by a wavelet transform of the signal (Mallat, 1989).
The wavelet decomposition of signal (Daubechies,
1992) allows to approximate signal for various
resolutions, lower than the initial resolution of a
signal before the transformation. Fast wavelet
decomposition can be performed by the Mallat
algorithm, shown in figure 1.
Figure 1: Wavelet decomposition by the Mallat algorithm.
At the first decomposition level it filtrates a
signal
with low- and high-pass filters and then
decimates the filtration results. This procedure
computations are very fast and give two coefficient
vectors: approximation
and detail
coefficients:
.1
At every following level the algorithm filtrates the
approximation of signal
(received at the
previous step) with low- and high-pass filters and
the results are also down-sampled, i.e.:
.2
As noticed by Mallat, the multiresolution
representation of a signal or an image is a very
effective method of extracting information (Mallat,
1989). In figure 2 are presented two patterns (in the
first row) generating two classes of noised signals
(second row). The approximation
of signal at
4
th
decomposition level (third row) reveals a noticeable
division between classes, especially for 9
th
coefficient.
Figure 2: Two class patterns, noisy signals for 10
and wavelet approximation coefficients
of 4
th
level.
2.2 Direct Classifier with Reject Option
The local Bayesian classifier
with reject option
assigns a signal to one class from the set 1,2
or rejects it what is denoted by zero. The signal is
represented by a sequence of wavelet approximation
coefficients
. The classification rule
is given
by formula
1,
if1
0,
ifmin
,1
2,
if
3
where the posterior probability of assigning a
signal to class 1, after observing values of wavelet
coefficient vector , is
.4
The posterior probability of assigning a signal to
class 2 is equal to 1
. The prior probabilities
of class occurrences are
and
. The probability
density functions in both classes are given by
and
.
The classification rule (3) can be transformed
into the following form
1,
if
∈
1,1
0,
if
∈
,1
2,
if
∈
0,
5
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
290

what leads to the one-stage local decision rule in the
multistage algorithm, defined in the next section 2.3.
2.3 Multistage Algorithm
The multistage algorithm has the following form:
Algorithm 1. Multistage Classifier
1: for from to 1
{
2: if
∈1,1
then class=1
END
3: if
∈,1
then class=0
GO TO STEP 1
4: if
∈0,
then class=2
END
}
5: return class
The maximum number of stages is . There will be
less stages if the posterior probability achieves an
appropriate level, dependent on the rejection
threshold .
2.4 Theoretical Risk
The difference between risk values for Bayes
classifiers with and without reject option (Libal,
2012), denoted by
and respectively, is
(6)
min
,1
⋅
⋅
0,
where
is the rejection area if the signal is
represented by a vector and the rejection threshold
is fixed to . The area
∅ only if there is
available the reject option, i.e. ∈0,0.5. If
0.5, there is no reject option and the area
∅ is an empty subspace of a feature space.
Examples of rejection areas are presented in figures
3 and 4.
3 EXPERIMENTS
There were 3 multistage classifiers tested with the
basic decision rules as:
1) naive Bayes,
2) linear discriminant analysis (LDA),
3) quadratic discriminant analysis (QDA).
Every one-stage rule was performed under
assumption that all features (i.e. wavelet
approximation coefficients on a fixed decomposition
level) are pairwise uncorrelated. The algorithm has 4
stages and the signals of length 128 were
decomposed for 4 levels by the Daubechies wavelet
family of order 2 (
Daubechies, 1992). The signal was
represented (if it was necessary):
at 1
st
stage by
, (10 coefficients),
at 2
nd
stage by
, (18 coefficients),
at 3
rd
stage by
, (34 coefficients),
at 4
th
stage by
, (65 coefficients).
The figures 3 and 4 shows in 2D the partition of
a feature space into decision areas of class 1 and 2
and rejection area, but the dimensionality of feature
space in performed experiments was always higher,
i.e. depending on the stage there were 10, 18, 34 or
65-dimensions.
Figure 3: Decision areas for classes and rejection area
(between lines) for LDA.
Figure 4: Decision areas for classes and rejection area
(between curves) for QDA.
MultistageNaiveBayesClassifierwithRejectOptionforMultiresolutionSignalRepresentation
291
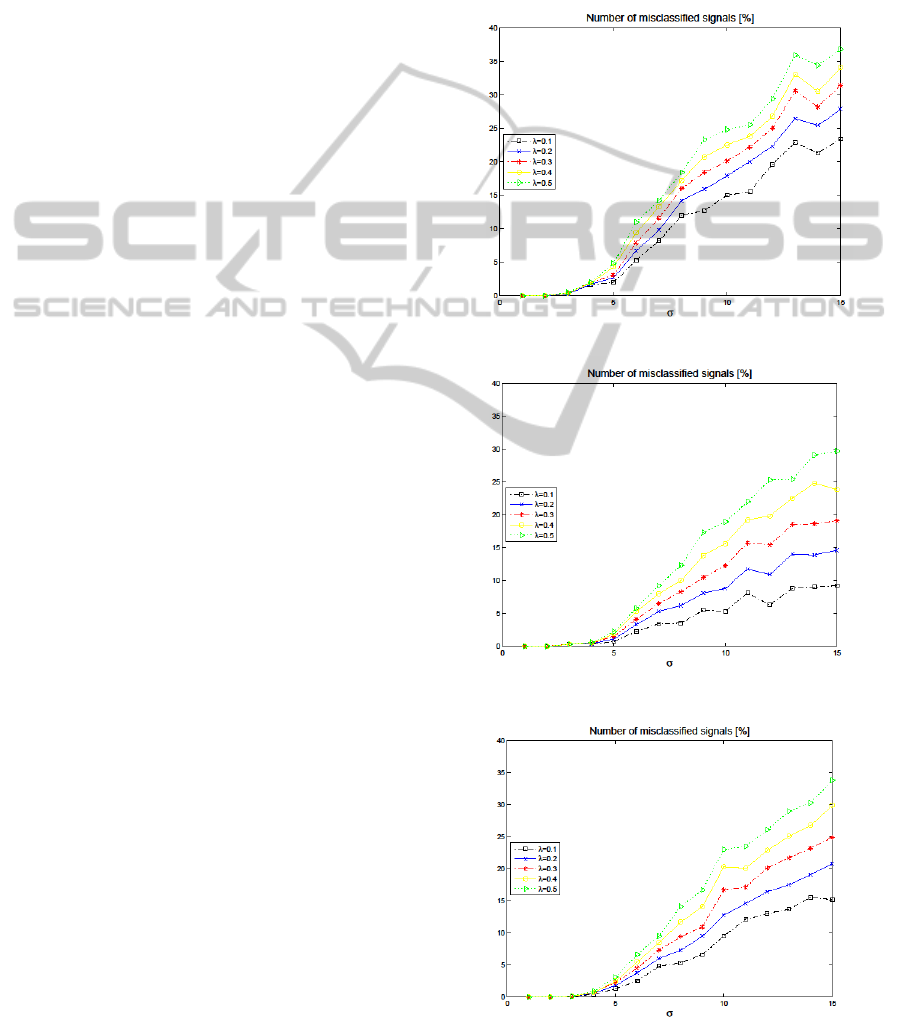
4 CONCLUSIONS
According to the inequality (6) the theoretical risk of
one-stage Bayes classifier without reject option is
higher than or equal to the risk of classifier
with
reject option, i.e.
.7
This fact has been confirmed by the experimental
results. In the figures 5, 6 and 7 is shown the risk of
incorrect classification of signals, containing class
patterns and a Gaussian white noise at the level of
(see figure 2). For the multistage classifier (i.e. for
0.1,0.2,0.3 and 0.4) the risk values from all
four stages were summarized. At the last stage
classifier has to choose a class from 1,2, so there
were no unclassified signals at the end. For 0.5
the classifier has no reject option and only one-stage.
The rejection threshold is a suffered loss after
rejecting a signal (choosing class 0). The loss after
choosing a wrong class from the set 1,2 is 1, and
there is no loss after choosing a correct class, what
means that the loss is equal to 0 then.
The lower the , the lower the risk of
misclassification. The application of the presented
classifier (given by algorithm 1) for wavelet
representation of signals improves the classifier
efficiency (see figures 5, 6 and 7). The lowest values
of experimental risk among the three methods were
obtained for linear discriminant analysis (LDA).
REFERENCES
Burduk, R. and Kurzyński, M., (2006). Two-stage binary
classifier with fuzzy-valued loss function. Pattern
Analysis & Applications, 9(4), pp.353-358.
Daubechies, I., (1992). Ten Lectures on Wavelets. Lecture
Notes Vol. 61, SIAM, Philadelphia.
Devroye, L. Györfi, L. and Lugosi, G., (1996). A
probabilistic theory of pattern recognition. Springer-
Verlag, New York.
Kurzyński, M., (1988). On the multistage Bayes classifier,
Pattern Recognition, 21(4), pp.355-365.
Libal, U., (2010). Multistage classification of signals with
the use of multiscale wavelet representation. In
MMAR’10, 15th IEEE Int. Conference on Methods
and Models in Automation and Robotics, pp.154-159.
Libal, U., (2012). Multistage pattern recognition of signals
represented in wavelet bases with reject option. In
MMAR’12, 17th IEEE Int. Conference on Methods
and Models in Automation and Robotics, pp.79-84.
Mallat, S.G., (1989). A theory for multiresolution signal
decomposition: the wavelet representation. Pattern
Analysis and Machine Intelligence, IEEE Transactions
on, 11(7), pp.674-693.
Pudil, P., Novovicova, J., Blaha, S., Kittler, J., (1992).
Multistage pattern recognition with reject option. In
Pattern Recognition, Vol.II. Conference B: 11th IAPR
Int. Conference on Pattern Recognition Methodology
and Systems, pp.92-95.
APPENDIX
Figure 5: Risk for naive Bayes classifier.
Figure 6: Risk for linear discriminant analysis (LDA).
Figure 7: Risk for quadratic discriminant analysis (QDA).
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
292
