
Resonant Acoustic Sensor System for the Wireless Monitoring
of Injection Moulding
F. M¨uller
1
, P. O’Leary
2
, G. Rath
2
, C. Kukla
3
, M. Harker
2
, T. Lucyshyn
1
and C. Holzer
1
1
Chair of Polymer Processing, Montanuniversitaet Leoben, Otto Gloeckel-Strasse 2, Leoben, Austria
2
Chair of Automation, Montanuniversitaet Leoben, Leoben, Austria
3
Industrial Liasion Department, Montanuniversitaet Leoben, Leoben, Austria
Keywords:
Pattern Recognition, Gibbs Error, Discrete Fourier Spectrum, Orthogonal Complement, Covariance Propaga-
tion, Discrete Fourier Transform.
Abstract:
The production of high quality plastic parts requires in-mould sensors to monitor the injection moulding pro-
cess. A novel wireless sensor concept is presented where structure borne sound is used to transmit information
from the inside of an injection mould to the outside surface, eliminating the need for cabling within the mould.
The sound is acquired and analyzed using new algebraic basis function techniques to enable the detection of
temporal occurrence of frequency patterns in the presence of large levels of noise. The temporal occurrence
of the resonators represents the passing melt front. The reduction of spectral leakage is computed by an al-
ternative method using low degree Gram polynomials. The computation of the pattern matching algorithm
yields both the correlation coefficients and their covariances which are used to determine the certainty of the
measurement. The paper presents the used mathematical background as well as real measurements performed
on an injection moulding machine. A test mould was equipped with two different resonant structures. Be-
sides calculating the correlation coefficients the 3σ confidence interval of the coefficients is computed. With
the novel algebraic approach a reliable separation of the two temporal points of occurrence of the resonant
structures was computed.
1 INTRODUCTION
Injection moulding is the most important manufactur-
ing process for plastic parts. In this highly dynamic
process a lot of effort went into the development of the
control algorithms of the injection moulding machine
concerning repeatability (Chen and Turng, 2005; Gi-
boz et al., 2007; Kamal et al., 1984). In contrast
the injection mould is often neglected in terms of
implementing control elements in form of sensors.
There are mainly two types of in-mould sensors that
are common, cavity wall temperature- and pressure-
sensors (Giboz et al., 2007) which always transmit
the measured values by wires. Since wires have some
disadvantages concerning mould design and mainte-
nance effort (Zhang et al., 2005), current research in
the field of wireless in-mould sensors presents differ-
ent approaches (Bulst et al., 2001; Gao et al., 2008;
Zhang et al., 2005).
In this paper a different approach is shown where
no active circuitry within the mould is required
(M¨uller et al., 2012). A distinctive structure borne
sound is generated on purpose by a mechanical res-
onator which is excited by the passing melt front.
Hence, the temporal event when the melt front passes
the resonator can be detected. This temporal resolu-
tion of the passing melt front is of special interest for
example for detecting the switch over point (from fill-
ing to holding pressure phase) or for hot runner bal-
ancing (Kazmer et al., 2010; Frey, 2004).
The main contributions of this paper are:
1. A new sensor concept is presented for wireless
monitoring of the filling of moulds during injec-
tion moulding;
2. Structure borne sound is used to implement wire-
less transmission of information from multiple
positions to a single accelerometer mounted out-
side the mould. This eliminates the need for ca-
bling within the mould, making the mould both
cheaper in construction and simpler to service;
3. The design of a mechanical resonator is combined
with a new signal processing method to enable
the detection of multiple events in the single time
153
Müller F., O’Leary P., Rath G., Kukla C., Harker M., Lucyshyn T. and Holzer C..
Resonant Acoustic Sensor System for the Wireless Monitoring of Injection Moulding.
DOI: 10.5220/0004266301530161
In Proceedings of the 2nd International Conference on Sensor Networks (SENSORNETS-2013), pages 153-161
ISBN: 978-989-8565-45-7
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
varying signal;
4. A new algebraic approach to the implementa-
tion of frequency domain pattern matching is pre-
sented. The new approach yields a numerically
very efficient solution to computing the desired
correlation coefficients. Furthermore and very im-
portant for measurements in an industrial environ-
ment, the new method also yields a method for
estimating the covariance of the correlation coef-
ficients. Consequently, the detection of an event
can be made with a given certainty.
2 PRINCIPLE OF OPERATION
The aim is to develop a system which is capable of de-
tecting when the melt front reaches specific regions in
a mould, i.e. the detection of discrete temporal events.
Multiple detections should be possible and there is
the further desire not to have any cabling within the
mould. This makes the mould simpler in construc-
tion and easier to service. The principle of operation
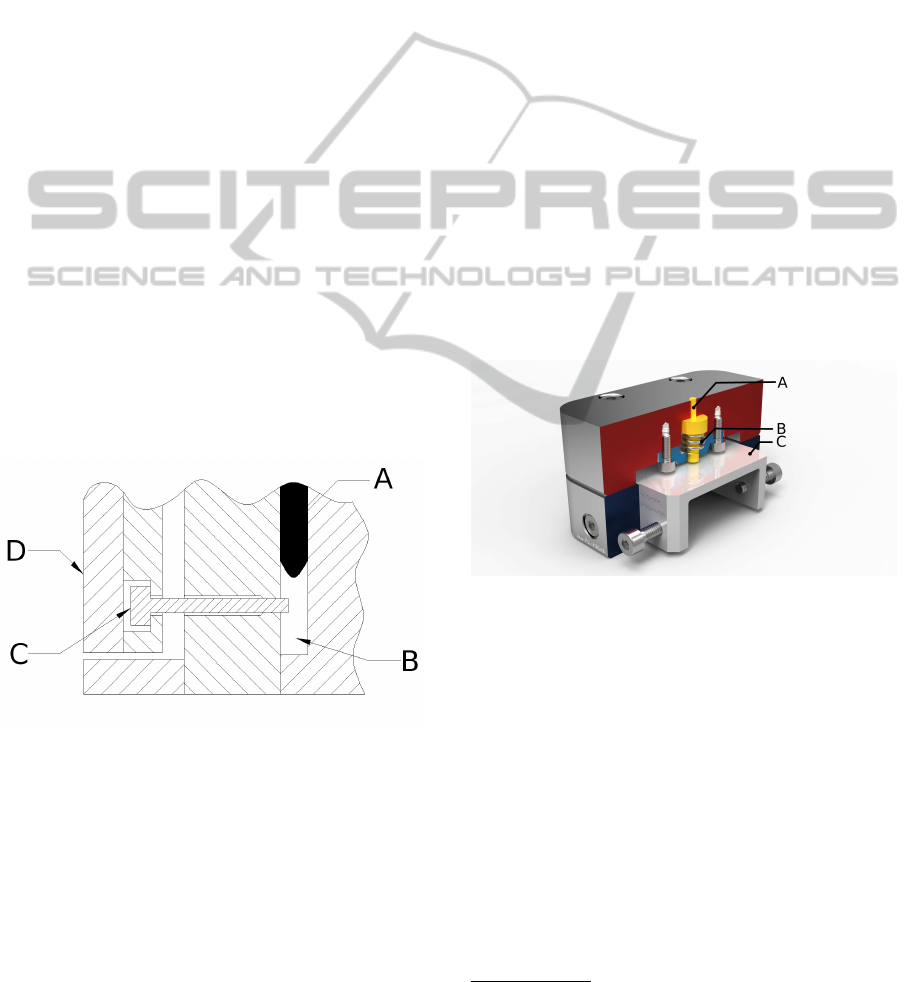
is very simple, see Figure 1: The dark portion in the
figure represents the melt (A) filling the cavity (B).
When the melt reaches the pin (C) it is depressed and
excites the resonator (D), which injects a characteris-
tic sound into the metal mass of the mould. This por-
tion of the system is purely mechanical. The sound is
acquired using a single accelerometer and analyzed.
Figure 1: Schematic drawing of the principle of operation.
The dark portion (A) represents the melt filling the cav-
ity (B). When the melt reaches the pin (C) it is depressed
and excited the resonator (D). This portion of the system is
purely mechanical (M¨uller et al., 2012).
The sensor system consists of three main portions:
1. Mechanical resonators, these are purely mechani-
cal devices which exhibit a characteristic damped
oscillatory behaviour. When excited they res-
onate and introduce structure borne sound into the
metallic mass of the mould.
2. A single accelerometer mounted on the outside of
the mould. This accelerometer detects the struc-
tural borne sound from all the mechanical res-
onators.
3. A signal acquisition and processing unit, which
acquires the signal from the accelerometer and
implements a new matrix algebraic approach to
pattern recognition. The system enables the detec-
tion of the time points of excitation of the different
mechanical resonators and with this the detection
of the melt front at the desired points in the mould.
This paper presents the development of the com-
plete detection system.
2.1 Mechanical Resonator
In Figure 2 a rendered section view of a mechanical
resonator is shown. The system consists of: a sprung
movable pin (A and B), and a resonant body (C). The
spring ensures the pin is in the correct position prior to
excitation. When the melt reaches the position in the
mould where the pin is, it accelerates the pin and ex-
cites the resonant body. The pin, spring and resonant
body form a damped resonator which emits a charac-
teristic acoustic signal into the metallic body of the
mould.
Figure 2: Rendered section view of one of the implemented
mechanical resonators. The pin (A) which is pushed by the
melt, the spring (B) which positions the pin and the reso-
nant body (C). This Figure shows the implemented 12[kHz]
resonator (M¨uller et al., 2012).
Two different resonator designs were imple-
mented for test purposes
1
:
1. A plate resonator, as shown in Figure 2, with a
primary resonant mode at 12[kHz], and
2. a tongue resonator, not shown, with a primary res-
onant mode at 3.8[kHz].
Both designs use the same mechanical components
(housing, pin and spring), only the resonant body is
exchanged. In this manner different resonant char-
acteristics can be simply implemented. The different
1
For simplicity in the rest of the paper the two resonators
are identified by their primary modal frequency.
SENSORNETS2013-2ndInternationalConferenceonSensorNetworks
154

oscillatory characteristics enable the separation of the
events from the different resonators in the signal ac-
quired from one and the same accelerometer.
2.2 Acoustic Detection
A single accelerometer is mounted on the outside
of the mould. It detects the structure borne sounds
from all the resonators. The accelerometer (352A60
from PCB Piezotronics) has a frequency range from
5−60000[Hz] and was sampled
2
with f
s
= 120[kHz].
The high frequency range has been chosen to improve
the performance of the system in the presence of sig-
nificant acoustic disturbances associated with the op-
eration of the machine.
The high sampling frequency gives a larger num-
ber of spectral components which can be used in the
pattern recognition to detect the desired oscillations.
The resonators have multiple harmonics which yield
multiple correlated components in the frequency do-
main. However, the wider range of noise acquired
with the higher sampling frequency is uncorrelated.
Consequently, a better signal to noise ratio can be
achievedin this manner. The signal acquisition is syn-
chronized with the start of the injection process.
2.3 Signal Processing
The aim of the signal processing is to implement
optimal detectors, optimal in terms of noise perfor-
mance, for the characteristic oscillations of the res-
onators. Due to the complex mechanical form and
internal reflections within the mould, the signals from
the resonators are not fully orthogonal. Consequently
classical correlation detectors (Fano, 1951) will not
function optimally. This paper presents a new al-
gebraic approach to signature recognition, which is
numerically efficient, while maintaining the advan-
tages of full spectrum pattern matching. In addition to
the matching of the pattern the new method also im-
plements the covariance propagation, which in turn
yields a confidence interval. Consequently, the cer-
tainty of the measurement is also determined. The
details are presented in the following section.
3 MATHEMATICAL
FRAMEWORK
In this paper a new algebraic implementation of a fre-
quency domain signature matching is implemented.
2
For test purposes the signal was acquired using a data
acquisition box from National Instruments (USB-6366).
There are two steps involved in signature matching:
1. Signature identification, i.e. identifying the op-
timal frequency domain signatures for each res-
onator. This task is performed a-priori to the mea-
surement and can be considered as a calibration of
the system.
2. Signature matching, which is formulated as a lin-
ear matrix algebraic computation. This method is
numerically efficient and the covariance propaga-
tion for the linear operator can be computed.
Before proceeding to these two steps it is neces-
sary to introduce a matrix algebraic approach to com-
puting a discrete Fourier transform (DFT) and a new
method for reducing the effects of the Gibbs phe-
nomena. In most common literature on digital signal
processing, e.g., (Press et al., 2002; Oppenheim and
Schafer, 1989), the computation of the DFT is formu-
lated as,
s(k) =
N−1
∑
n=0
y(n)e
− j2πkn/N
(1)
whereby, y(n) is the n
th
sample of the input signal, N
is the total number of samples available, and k defines
the discrete frequency f
k
= (2πkn/N) f
s
, with respect
to the sampling frequency f
s
. Given N input samples
there are N components in the discrete Fourier spec-
trum. Computing the discrete Fourier series is most
commonly called the discrete Fourier transform and
is most commonly implemented using the fast Fourier
transform (FFT) algorithm. The FFT and DFT are
functionally identical, the FFT is simply a numeri-
cally more efficient method of performing the com-
putation.
The computation of the DFT can also be formu-
lated as a matrix
3
operation. The discrete Fourier ba-
sis functions f(k),
f(k) , e
− j2πkn/N
, (2)
can be concatenated forming the columns of a matrix
F, such that
4
,
F ,
f(0),... , f(N − 1)
. (3)
Now given a vector y of N input samples, the com-
plete spectrum s, a vector, of the signal y is computed
as,
s = F y. (4)
Computing the discrete Fourier spectrum in this man-
ner is significantly less efficient than computing an
3
A brief note on nomenclature: matrices are indicated
by sanserif capital letters, e.g. H, and vectors by sanserif
lowercase letters, e.g. y.
4
The matrix F can be generated in MATLAB using the
code, F = dftmtx(N)
′
.
ResonantAcousticSensorSystemfortheWirelessMonitoringofInjectionMoulding
155

FFT if finally all spectral components are required.
However, as shall be seen, given the need to only
identify a low number of signatures the method offers
significant advantages, both with respect to numerical
efficiency as also in estimating confidence intervals.
Prior to computing the spectrum it is necessary to
take measures so as to limit the errors associated with
the Gibbs phenomena. The classical approach is to
use windowing (Press et al., 2002; Lindquist, 1988),
however, a new method based on polynomial approx-
imation was introduced recently, see (O’Leary and
Harker, 2011) for derivations and exact nature of the
computation. The signal is projected onto the orthog-
onal complement of a set of Gram polynomial basis
functions of low degree. The Gram polynomial ba-
sis functions up to degree d are also used to form the
columns of a matrix G
d
, the projection P onto the or-
thogonal complement can be computed as,
P = I − G
d
G
T
d
, (5)
where I is the unit matrix.
The spectrum with reduced spectral leakage is
now computed as,
s = F
I − G
d
G
T
d
y. (6)
It should be noted that, H , F
I − G
d
G
T
d
is once
again a matrix. In this manner reducing the Gibbs
effect has added no additional numerical complexity,
since H can be computed a-priori.
3.1 Signature Identification
The calibration procedure takes advantage of super-
position, in the assumption that the noise of the ma-
chine and the sound from the resonator can be re-
garded as additive signals. The i
th
resonator alone is
artificially activated while the machine is not running.
The signal from the accelerometer is acquired and the
corresponding spectrum is computed,
s
i
= H y. (7)
This procedure is repeated for each resonator yield-
ing a set of n initial spectral signatures one for each
resonator. Unfortunately, due to the complicated me-
chanical forms and internal acoustic reflections within
the form these vectors are not fully orthogonal.
The orthogonality of the signatures is achieved by
projecting them onto their mutual orthogonal comple-
ments. Given n signatures this is computed as,
ˆs
i
=
(
I −
∑
k
s
k
s
T
k
!)
s
i
∀ k ∈ [1. .. n],k 6= i. (8)
To support understanding it is helpful to formulate
this computation for two signatures,
ˆs
1
= s
1
− s
2
s
T
2
s
1
=
I − s
2
s
T
2
s
1
(9)
ˆs
2
= s
2
− s
1
s
T
1
s
2
=
I − s
1
s
T
1
s
2
. (10)
This computation yields a set of n orthogonalized sig-
natures ˆs
i
, which are complex vectors each of length
N. These are then used in the signature matching pro-
cess. The matrix of signatures S is formed by con-
catenating the individual orthogonalized vectors and
dividing them by their norm,
S =
h
ˆs
1
|ˆs
1
|
,.. .,
ˆs
n
|ˆs
n
|
i
. (11)
In this manner the matrix S has a unitary norm. Con-
sequently, S
+
, which is discussed next, has also a uni-
tary norm.
The orthogonalization process described by Equa-
tions 9 and 10 have worked well with the sensors used
in the experiment presented in this paper. However,
other experiments suggest that a diagonalisation of
the matrix of signatures, using singular value decom-
position, yields an even better separation of the sig-
nals with a lower cross sensitivity. This issue, how-
ever, is still the subject of further investigation.
3.2 Signature Matching
To support understanding it is helpful to take a more
fundamental look at the nature of the system and the
computation being performed. The excitation of the
pin can be approximated as a dirac pulse, in this case
the signatures correspond to the impulse response of
the resonators. For simplicity the orthogonalization
process is not considered now. The impulse response
corresponds to the first eigenfunction of the differ-
ential equation describing the dynamics of the res-
onator. Given a measurement of the resonator’s re-
sponse, with the addition of noise, the task is to per-
form de-convolution of the measured signal with the
response of the differential equation. This is funda-
mentally an inverse problem. In a lose sense it is
equivalent to inversion of the stochastic differential
equation for the system.
An algebraic approach to the computation has
been chosen since the Moore-Penrose pseudo-
inverse (Golub and Van Loan, 1996) provides a least
square approximation for the inversion of a rectangu-
lar matrix,
S
+
,
S
T
S
−1
S
T
, (12)
which ensures,
S
+
S = I. (13)
Computing S
+
is akin to inverting the eigenfunctions
s
i
contained in S which describe the differential equa-
tions of the resonators.
SENSORNETS2013-2ndInternationalConferenceonSensorNetworks
156

The input signal is continually acquired and a sub-
set of N values are selected to form the vector y. The
spectrum of the signal is computed as shown in Equa-
tion 6,
s
t
= H y. (14)
This is called the temporal varying signature s
t
. It
should be noted that it may contain zero or any num-
ber of the sought events. The correlation coefficient
to the n signatures is computed as,
c = S
+
s
t
= S
+
Hy, (15)
where c is an n element column vector
5,6
. The ma-
trix L can now be defined as L , S
+
H, this is of size
N × n, in the test case here n = 2 and N = 600. This
matrix is computed a-priori to measurement; conse-
quently computing the correlation coefficients at run-
time is numerically very efficient and can be written
as,
c = L y. (16)
The computation is repeated p samples later.
Computation in this manner is very closely related
to the short-time Fourier transform (STFT). For those
more familiar with classical digital signal processing:
the columns of L can be considered to be the coef-
ficients of a finite impulse response (FIR) filter (Op-
penheim and Schafer, 1989), with a decimation factor
p. Consequently, there is a bank of n FIR filters given
n resonators.
3.3 Covariance Propagation
The covariance (Brandt, 1998) for a vector is defined
as,
Λ
c
, {c − E(c)} {c − E(c)}
T
. (17)
Now substituting the relationship c = Ly, yields,
Λ
c
= {Ly − L E(y)} {Ly − L E(y)}
T
, (18)
and factoring out L,
Λ
c
= L {y − E(y)} {y − E(y)}
T
L
T
. (19)
5
To facilitate numerical efficiency the correlation coeffi-
cients can be computed as,
c = S
+
abs(Hy).
The norm of
S
+
is 1 and the norm of |H| = 1− 2/n, in the
application n = 600, therefor |H| ≈ 1. Consequently, this
numerical simplification does not change the norm of the
result.
6
Ideally this computation should yield only real values
for c; however, due to numerical errors small imaginary
components may remain. For this reason, it is suggested
to take only the real portion, i.e., R (c).
By definition Λ
y
, {y − E(y)} {y − E(y)}
T
, conse-
quently,
Λ
c
= L Λ
y
L
T
. (20)
If we can regard the input noise to the system as inde-
pendent identically distributed (i.i.d.) Gaussian errors
with standard deviation σ, the covariance of the input
is given by,
Λ
y
= σ
2
I, (21)
and consequently,
Λ
c
= σ
2
LL
T
. (22)
In this manner we also have an estimator for the co-
variance of the correlation coefficients. This is one of
the major advantages of using an algebraic approach
to solve this problem. No other computation method
would yield the covariance estimates in such a simple
manner.
3.4 Decision Process
Given the vector of correlation coefficients c and the
associated covariance matrix Λ
c
: a decision with a de-
sired confidence interval can be made.
There is a delay of N samples for the first deci-
sion and then a decision follows every P samples. The
group delay for an FIR filter with N symmetric coeffi-
cients is t
d
= N/(2 f
s
), for example in this application
with f
s
= 120[kHz] and a signature length of N = 600
there is a decision delay of t
d
= 2.5[ms] and a new de-
cision is available every t
r
= 0.42[ms].
4 EXPERIMENTAL SETUP
AND RESULTS
The experiments were performed on an Arburg in-
jection moulding machine (470A-1000) with a Poly-
Propylen (C7069-100NA) from Dow. The injection
speed was set to 60[cm
3
s
−1
]. The diameter of the
injection screw is 40[mm]. For the measurements a
test mould was built. The mould consists of two sym-
metrical cavities which are gated by a hot runner sys-
tem (Johannaber and Michaeli, 2004). The hot runner
system is equipped with an electromagnetic valvegate
control. Two test resonators with different designs
were implemented and installed in the test mould.
Figure 3 shows a picture of the clamped mould in
the injection moulding machine. The mould is shown
in the opened position. During processing the mould
is closed and charged with a clamping force of ap-
proximately 900[kN]. The two symmetric cavities are
indicated by A and B. The accelerometer in the pic-
ture is marked with C, which is mounted on the out-
side surface of the mould.
ResonantAcousticSensorSystemfortheWirelessMonitoringofInjectionMoulding
157

Figure 3: Picture of the mould clamped in the injection
moulding machine. The mould is shown in opened posi-
tion. During the production process the mould is closed and
charged with a clamping force of approximately 900[kN].
A and B indicate the two symmetrical cavities; C marks the
position of the accelerometer mounted on the outside sur-
face of the mould.
4.1 Experimental Signature
Identification
The machine is not running during identification of
the signatures. This reduces the spurious presence
of noise during this process. Since there are two
resonators implemented in the mould n = 2. As
previously mentioned a sampling frequency of f
s
=
120[kHz] was used. Both resonators were excited in-
dependently and their time response was measured.
In Figure 4 the time response as a function of time
for both resonators is shown. It is important to note
that the resonator nominally designed for 3.8[kHz]
has many overtones which lead to higher frequency
components than the 12[kHz] resonator.
The sampled data was segmented into packets
containing N = 600 samples. Each packet is projected
onto the orthogonal complement of a Gram polyno-
mial G
d
of degree d = 1 prior to computing the cor-
responding discrete Fourier spectrum, this suppresses
significant portions of the spectral leakage. The ob-
tained signatures are not fully orthogonal due to the
complex mechanical form of the mould as well as
acoustic reflections inside it.
Therefore the two signatures are then orthogonal-
ized according to Equations 9 and 10. The result-
ing orthogonalized signatures are shown in Figure 5.
Since the magnitude spectrum of a real signal is sym-
metric, only the first N/2, i.e., 300 values are shown.
From the spectrum it gets clear, that there are just
significant frequency components up to approximatly
20[kHz]. With a given sampling rate of 120[kHz]
0 1 2 3 4 5
−0.2
0
0.2
y
1
(t)
0 1 2 3 4 5
−0.5
0
0.5
y
2
(t)
Time [m s]
Figure 4: Top: the time response of the 12[kHz] resonator.
Bottom: the time response of the 3.8[kHz] resonator. It is
important to note that the resonator nominally designed for
3.8[kHz] has many overtones. This lead to higher frequency
components. Each of the time signatures consists of 600
samples. The shown results were measured independently
and are not shown synchronized.
this means that just the first 50 values of the spec-
trum are required for event identification. Since the
noise is distributed over 600 values of the spectrum
and just 50 of them are needed, this corresponds to
an implicit regularization. This yields a noise gain of
g
n
=
p
50/600.
The two orthogonalized signatures, ˆs
1
(ω) and
ˆs
2
(ω), are used during further processing.
0 10 20 30
0
0.2
0.4
ˆs
1
(ω)
0 10 20 30
0
0.2
0.4
ˆs
2
(ω)
Frequency [kHz]
Figure 5: Top: the spectrum of the impulse response of the
12[kHz] resonator. Bottom: the spectrum of the impulse re-
sponse of the 3.8[kHz] resonator. Here, as in Figure 4, the
higher frequency components associated with the harmon-
ics of the 3.8[kHz] are visible in the spectrum. Note there
are only significant magnitudes in the range up to approxi-
mately 20[kHz]. Given the sampling frequency of 120[kHz]
this means only 50 components are required to identify the
events. This corresponds to an implicit regularization, the
noise is distributed over 600 of which only 50 are used. This
yields a noise gain of g
n
=
p
50/600.
4.2 Experimental Signature Matching
During signature matching the machine is running
and the process is subject to large levels of spurious
noise emitted from the mechanisms of the injection
SENSORNETS2013-2ndInternationalConferenceonSensorNetworks
158
moulding machine and process. At the beginning of
the injection moulding cycle the valves are opened
which results in a large excitation of the time signal
at the beginning of the measurement (see beginning
of Figure 6). Despite having a fully symmetrical flow
channel system there will be an unbalanced filling
of the cavities, having tolerances and inhomogeneous
temperature distributions (Johannaber and Michaeli,
2004). To compensate the unbalanced filling and en-
sure simultaneous filling of both cavities the valves
are opened consecutively whereby the opening delay
is controlled by a closed loop controller. In each of
the cavities a resonator is implemented, the left cav-
ity with the 12[kHz] resonator, the right one with the
3.8[kHz] resonator.
The measurements were synchronized to the start
of the injection moulding process. The data acquisi-
tion box records the accelerometer channels for a du-
ration of 10[s]. The first 2[s] of the recorded signal
are shown in Figure 6. It can be seen that the signal
is perturbed with large levels of noise. It is assumed
that the noise is distributed as i.i.d. Gaussain noise
with σ = 1.6e−4.
0 0.5 1 1.5 2
−1
−0.5
0
0.5
1
Time [s]
y(t) [V]
Figure 6: First 2[s] of recorded accelerometer signal shown
in time domain. The signal is perturbed with noise over the
whole measurement. The noise is assumed as i.i.d Gaussian
noise, σ = 1.6e−4. The searched resonators both appear in
the time domain at approximately 1.1[s] after start of the
filling phase. The exact time point is estimated with the
correlation coefficient computation.
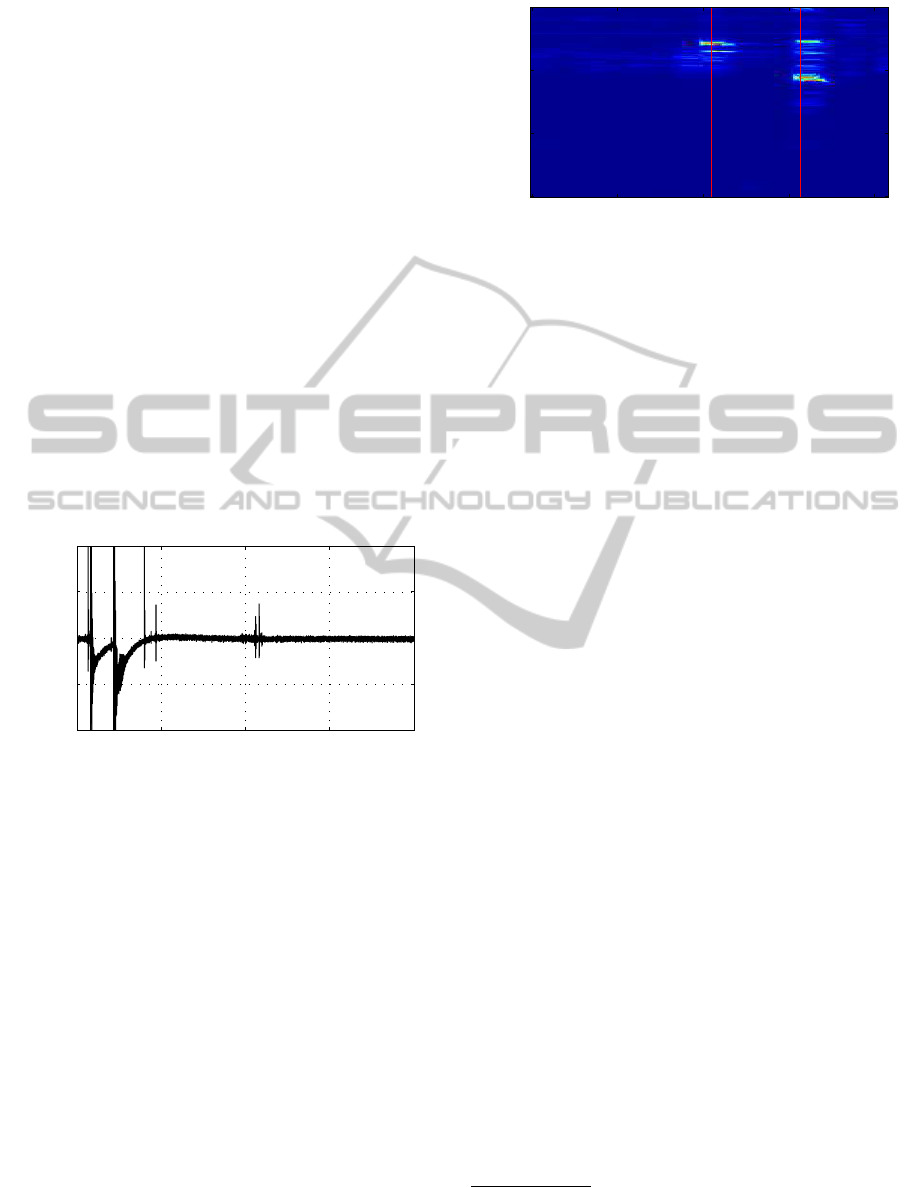
To support understanding, the short time Fourier
transform (Spectrogram) of the signal is computed
and shown in Figure 7. Thereby just the period
where the frequency patterns are expected is shown
in the spectrogram. At approximately 1.06[s] the
12[kHz] resonator is found, at approximately 1.08[s]
the 3.8[kHz] resonator. The temporal positions of the
events were identified using signature matching, i.e.
via the correlation coefficients which are discussed
later. This visualization is not required during normal
operation.
The correlation coefficients were computed as
proposed in Equation 15 and are shown with a
Frequency [kHz]
Time [s]
STFT
3.8 kHz12 kHz
1.02 1.04 1.06 1.08 1.1
0
20
40
60
Figure 7: Magnitude spectrogram of the accelerometer sig-
nal, in addition the time points when the resonator events
occurred are shown, for both the 3.8[kHz] and 12[kHz] res-
onators. The temporal positions of the events were identi-
fied using the signature matching, i.e. via the correlation
coefficients.
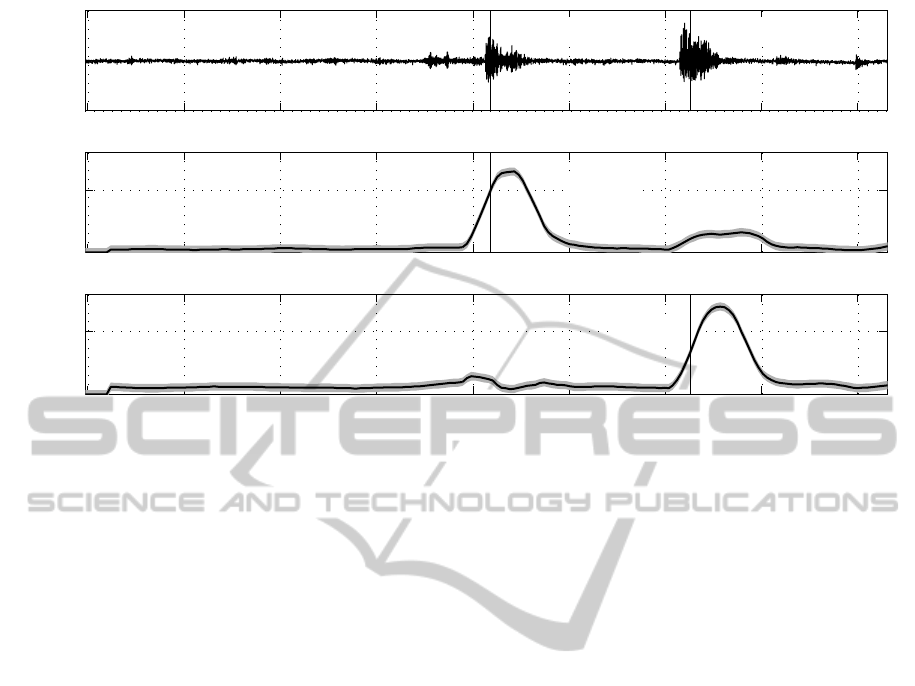
3σ (99.73%) confidence interval in Figure 8 (mid-
dle: c
1
(t) for the 12[kHz] resonator; bottom: c
2
(t) for
the 3.8[kHz] resonator). The top diagram shows the
recorded data y(t) in the time domain.
Regarding c
1
(t), the solid black line indicates the
computed coefficients. In addition, a gray band indi-
cates the 3σ (99.73%) confidence interval. The con-
fidence interval is calculated by the covariance matrix
Λ
c
, which is computed after Equation 22 as,
Λ
c
=
0.91630 0.79795
0.79795 0.91630
. (23)
Since the matrix Λ
c
is symmetric and has the identi-
cal values in the diagonal, a symmetric 3σ(99.73%)
confidence interval for both components, i.e. c
1
(t)
and c
2
(t), is calculated as ±2.8.
The value of c
1
, corresponding to the 12[kHz] res-
onator, stays at a low level up to 1.059[s] where a
peak appears. At 1.061[s] a black vertical line indi-
cates the detection of the 3.8[kHz] resonant structure.
The detection is computed with descriptive statistics
7
(Haase, 2002).
The second correlation coefficient c
2
, correspond-
ing to the 3.8[kHz] resonator, shows a peak starting at
1.080[s]. The temporal occurrence event was recog-
nized at 1.082[s].
For both detection events a cross correlation can
be observed. Since the cross correlations are small
compared to the peak values of c a reliable separation
of both events can be ensured.
Figure 8 (top) shows the time domain signal y(t)
of the recorded accelerometer data with indicated
events for both resonant structures. It has to be noted
7
Mainly the calculation of the standard deviation and the
skewness as well as a probability density function are used
for computing the detection.
ResonantAcousticSensorSystemfortheWirelessMonitoringofInjectionMoulding
159
1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.1
−0.5
0
0.5
y(t) [V]
3.8 kHz12 kHz
1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.1
0
50
12 kHz
c
1
(t)
1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.1
0
50
3.8 kHz
Time [s]
c
2
(t)
Figure 8: top: amplitude signal y(t) from the accelerometer, the time points for the identification of the two events are also
shown. Middle: the black line shows the correlation coefficient c
1
(t) for the 12[kHz] resonator as a function of time, the
gray region around the line is the 3σ, i.e., 99.73%, confidence interval for the correlation. Bottom: the black line shows the
correlation coefficient c
2
(t) for the 3.8[kHz] resonator as a function of time, the gray region around the line is the 3σ, i.e.,
99.73%, confidence interval for the correlation. Some cross sensitivity of the correlations can be observed. However, they are
sufficiently small to ensure a reliable separation of the two events.
that the coefficients c both start rising slightly before
the deflection of the time domain signal. This lead
from the fact that the signal is segmented into pack-
ets. These packets are evaluated at their center point.
In terms of the injection moulding process the
temporal detection point of the resonant structures in-
dicate the passing melt front.
5 CONCLUSIONS
In this paper a novel wireless in-mould sensor for in-
jection moulding was presented. The sensor is ca-
pable to detect the melt front at certain predefined
positions in the cavity. The data transmission is ob-
tained by the generation of distinctive sound which
is detected by an outside mould surface mounted ac-
celerometer. To separate multiple implemented sen-
sors a frequency pattern search is performed using a
new linear algebraic approach. This method yields a
numerically efficient approach for computing the cor-
relation coefficients. In addition, the covariance prop-
agation can be estimated which consequently yields
the computation of a confidence interval of the esti-
mated coefficients.
The proposed sensor system and the signal pro-
cessing were tested on an injection moulding ma-
chine. In the mould, two different resonant structures
were implemented. First the process of signature
identification was described. The obtained orthogo-
nalized signatures were used for the pattern match-
ing process. Injection moulding cycles were recorded
with an outside mounted accelerometer. The recorded
signal contains the sound of the resonators which is
superposed with large levels of noise from the ma-
chine, the mould and auxiliary units. However, the
described frequency domain pattern matching algo-
rithm was able to find both temporal points when the
resonant structures were excited. The detection of the
resonant structures corresponds to the detection of the
temporal moment of the passing melt front. In addi-
tion, the 3σ confidence interval of the computed cor-
relation coefficients was shown.
The process of orthogonalization of the signatures
yields space for further investigation with respect to
perturbation analysis, i.e. achieving optimal sensitiv-
ity for noise.
REFERENCES
Brandt, S. (1998). Data Analysis: Statistical and Computa-
tional Methods for Scientists and Engineers. Springer,
Berlin, 3rd edition.
Bulst, W.-E., Fischerauer, G., and Reindl, L. (2001). State
of the art in wireless sensing with surface acoustic
SENSORNETS2013-2ndInternationalConferenceonSensorNetworks
160

waves. IEEE Transactions on Industrial Electronics,
48(2):265–271.
Chen, Z. and Turng, L.-S. (2005). A review of current
developments in process and quality control for in-
jection molding. Advances in Polymer Technology,
24(3):165–182.
Fano, R. (1951). Signal-to-noise Ratio in Correlation
Detectors. Technical report (Massachusetts Institute
of Technology. Research Laboratory of Electronics).
Massachusetts Institute of Technology, Research Lab-
oratory of Electronics.
Frey, J. (2004). Method for automatically balancing the vol-
umetric filling of cavities. US Patent 2004/0113303
A1.
Gao, R., Fan, Z., and Kazmer, D. (2008). Injection mold-
ing process monitoring using a self-energized dual-
parameter sensor. CIRP Annals - Manufacturing Tech-
nology, 57(1):389–393.
Giboz, J., Copponnex, T., and M´el´e, P. (2007). Microin-
jection molding of thermoplastic polymers: a review.
Journal of Micromechanics and Microengineering,
17(6):96–109.
Golub, G. and Van Loan, C. (1996). Matrix Computations.
The Johns Hopkins University Press, Baltimore, 3
rd
edition.
Haase, S. (2002). Spectral and statistical methods for vi-
bration analysis in steel rolling. PhD Thesis Monta-
nuniversitaet Leoben.
Johannaber, F. and Michaeli, W. (2004). Handbuch
Spritzgiessen. Hanser, M¨unchen, 2nd edition.
Kamal, M. R., Patterson, W. I., Fara, D. A., and Haber, A.
(1984). A study in injection molding dynamics. Poly-
mer Engineering and Science, 24(9):686–691.
Kazmer, D. O., Velusamy, S., Westerdale, S., Johnston, S.,
and Gao, R. X. (2010). A comparison of seven filling
to packing switchover methods for injection molding.
Polymer Engineering & Science, 50(10):2031–2043.
Lindquist, C. S. (1988). Adaptive and Digital Signal Pro-
cessing with Digital Filtering Applications. Steward
& Sons.
M¨uller, F., Rath, G., Lucyshyn, T., Kukla, C., Burgsteiner,
M., and Holzer, C. (2012). Presentation of a novel
sensor based on acoustic emission in injection mold-
ing. Journal of Applied Polymer Science. In Press.
O’Leary, P. and Harker, M. (2011). Polynomial approxima-
tion: An alternative to windowing in fourier analysis.
IEEE Proceedings of I2MTC 2011.
Oppenheim, A. and Schafer, R. (1989). Discrete-Time Sig-
nal Processing. Prentice-Hall, Englewood Cliffs, NJ.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-
nery, B. P. (2002). Numerical Recipes in C++: The
Art of Scientific Computing. Cambridge University
Press.
Zhang, L., Theurer, C. B., Gao, R. X., and Kazmer, D. O.
(2005). Design of ultrasonic transmitters with de-
fined frequency characteristics for wireless pressure
sensing in injection molding. IEEE Transactions
on Ultrasonics Ferroelectrics and Frequency Control,
52(8):1360–1371.
ResonantAcousticSensorSystemfortheWirelessMonitoringofInjectionMoulding
161
