
Qualitative Vocabulary based Descriptor
Heydar Maboudi Afkham, Carl Henrik Ek and Stefan Carlsson
Computer Vision and Active Perception Lab., KTH, Stockholm, Sweden
Keywords:
Bag-of-Words Model, Image Classification.
Abstract:
Creating a single feature descriptors from a collection of feature responses is an often occurring task. As such
the bag-of-words descriptors have been very successful and applied to data from a large range of different
domains. Central to this approach is making an association of features to words. In this paper we present a
new and novel approach to feature to word association problem. The proposed method creates a more robust
representation when data is noisy and requires less words compared to the traditional methods while retaining
similar performance. We experimentally evaluate the method on a challenging image classification data-set
and show significant improvement to the state of the art.
1 INTRODUCTION
Most learning and inference algorithms require data
to be presented as points in a vector space. However,
in many scenarios data does not naturally lend itself to
such representations. One such example is when data
is represented as a collection of feature responses as
is common in Computer vision and natural language
processing. To be able to access and benefit from the
traditional learning techniques a common approach is
to translate the set of points and create a vector rep-
resenting the full collection of responses. When the
number of responses are fixed and can be assigned to
a specific order, the na¨ıve approach would be to con-
catenate the responses into one large vector. However,
this does not acknowledge that the responses comes
from the same domain. Neither is it likely that we
can induce a consistent order nor consistently recover
the same number of responses. A very simple, but
yet powerful method that overcomes these issues is
the bag-of-words model. The method requires that a
notion of similarity relating the elements in the col-
lection exist. Using this measure the space of features
can be discretized as a mixture of representative re-
sponses referred to as words. By associating each re-
sponse with a word a single feature vector can be con-
structed as the distribution of associations for the con-
stellation. This means that a single vector of a fixed
dimension can be constructed from constellation from
a varying number of elements. The standard bag-of-
words model used in computer vision is inspired from
the text and documents processing models (Russell et
al., 2006)(Sivic et al., 2005; Lazebnik et al., 2006).
These models usually assume that the effect of noise
with respect to word association and discovery is
neglect-able. While this might be a reasonable as-
sumption in text processing (Wang et al., 2005), it is
widely known that visual word discovery can be chal-
lenging due to the low level noise that exists in the im-
ages. The visual dictionary used to describe images is
often calculated using a clustering algorithm. Due to
the ambiguity that exist in the clustering algorithms
these words are not as well-defined as the words used
in text processing, which are usually selected from a
text dictionary. While the bag-of-word model relies
on the frequency of different words seen in the data,
resolving the ambiguity in visual word discovery can
be very beneficial.
In this paper we present a novel approach to con-
struct a fixed dimensional descriptor from a constel-
lation of feature responses within the bag-of-words
framework. Specifically, we will address issues re-
lating to the feature response to word association that
commonly present themselves for vision data by ac-
knowledging that word discovery is uncertain. The
proposed approach is related with feature pooling
methods such as (Boureau et al., 2010; Jarrett et al.,
2009) with the difference that in our work feature
pooling is not done on the statistics of occurrences
of the words but rather on feature responses that are
related to these words. These feature responses elim-
inate the ambiguity of features being assigned to dif-
ferent words in a way that each feature has a unique
response toward its associated word. In Sections 2
188
Maboudi Afkham H., Henrik Ek C. and Carlsson S. (2013).
Qualitative Vocabulary based Descriptor.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 188-193
DOI: 10.5220/0004266901880193
Copyright
c
SciTePress

Clustering
Local
Classifiers
Optimization
Vocabulary
Train
Dataset
Sift Features
Extract
Features
Image
Labeled
Features
Local
Evaluation
Feature
Pooling
Standard BOW
Proposed Descriptor
Label
Bagging
Figure 1: This figure compares the steps required for computing the bag-of-words histogram and the proposed descriptor.
Both methods use the same vocabulary for summarizing the image. Unlike bag-of-words model that relies on the frequency
of the words in the image, our method uses labeling produced by vocabulary for a local evaluation of the features and uses the
responses from this evaluation to summarize the image.
and 3 we will motivate and describe the proposed
descriptor. Section 4 we present a thorough experi-
mental evaluation and Section 5 concludes the paper.
2 RELATED WORKS
For a better understanding of the problem lets assume
that I is an image with {x
1
, . . . , x
n
} being a collec-
tion of features (Vedaldi and Fulkerson, 2008) ex-
tracted from it. In all different sections of this work it
is assumed that an already trained visual vocabulary
D = {w
1
, . . . , w
N
} is provided. Given this vocabulary
the mapping
l(x
i
) = argmin
w∈D
|x
i
− w|
2
, (1)
assigns each x
i
to its closest visual word in D. Having
this mapping each image is described using a N bin
histogram H, where the value of its i
th
bin is deter-
mined by
H[i] =
∑
x
k
∈I
(l(x
k
) == w
i
). (2)
As it can be seen every x
k
with similar l(x
k
) is
treated equally in this formulation. The down side
of this treatment is the fact the differences between
the features assigned to the same visual word are ne-
glected. It should be mentioned that this difference
does not appear in the bag-of-word models built on
text datasets since the words in the dictionary are
well-defined and are not the result of a generic clus-
tering algorithm. This ambiguity in assignment of
visual words has been addressed in many researches
(Zhang and Chen, 2009; Morioka and Satoh, 2010)
since the introduction of visual words in computer vi-
sion. Among the most influential works is the work
by (Savarese et al., 2006) in which they build a more
well-defined visual vocabulary by introducing rela-
tional spatial constraints in calculation of the vocab-
ulary. In their work they show that building such vo-
cabulary significantly improves the results. In other
approaches such as (Bouachir et al., 2009) the dif-
ferences between the features assigned to the same
words were highlighted by measuring the distance to
the closest cluster as a weight in calculation of Eq. 2
or using soft assigning each feature to several visual
words.
In this paper we take a slightly different approach
toward the bag-of-word models. While using the
same dictionary D, our approach is based on gath-
ering statistics of the quality of features assigned to
a certain visual word rather than their quantity. The
fundamental principle underpinning a bag-of-words
approach is that the elements of the dictionary D cap-
ture the local structures of the image. Here the goal is
to measure the quality of these structures with respect
to different target classes in a discriminative manner
and use this information to describe the image. In
other words the question being asked in this paper is
”How representative underpinning of the word is the
feature?” rather than ”How often a word is seen?”.
The assumption behind this work is that structures la-
beled as a certain visual word appear on different ob-
jects. This means there can be a significant difference
between them due to the fact that they have appeared
on completely difference objects. The difference be-
tween our method and the standard bag-of-words his-
togram can be seen in figure 1.
QualitativeVocabularybasedDescriptor
189
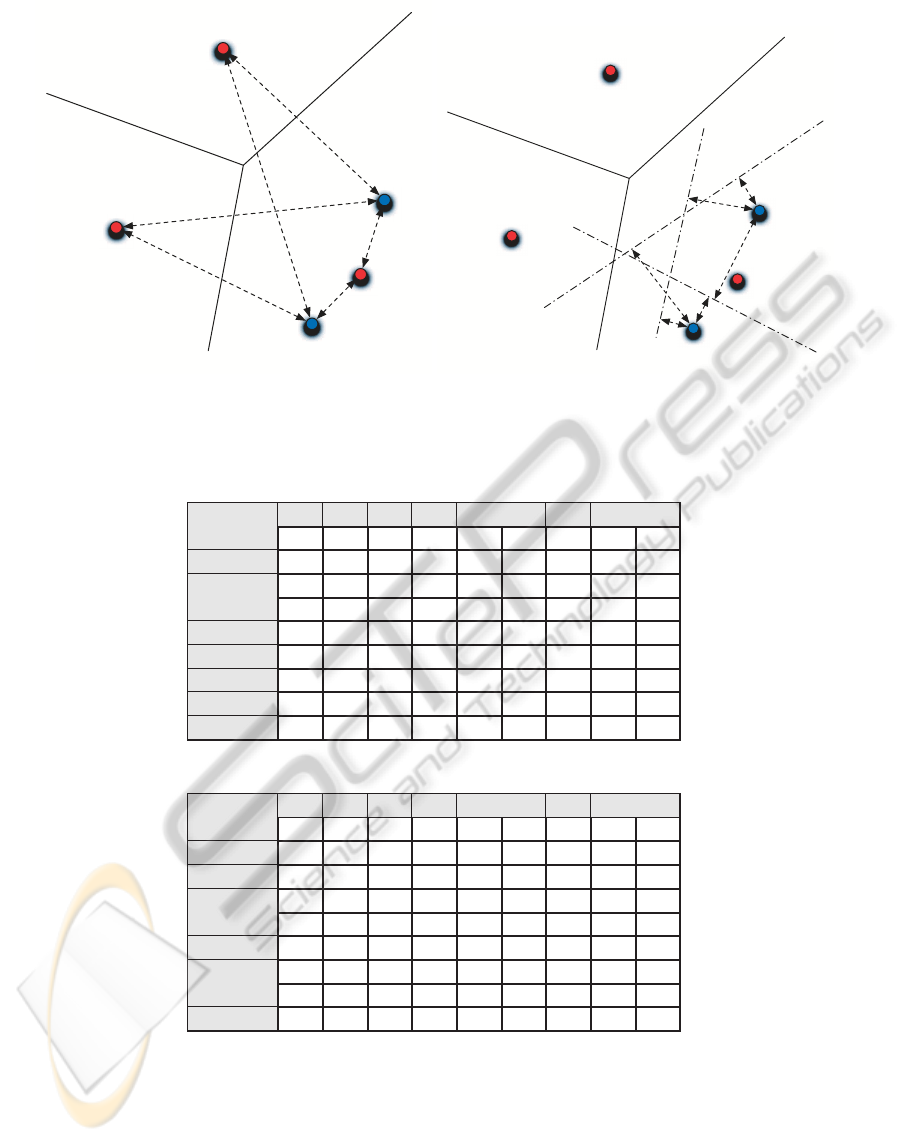
w
1
w
2
w
3
x
i
x
j
w
1
w
2
w
3
x
i
f
C
1
w
3
f
C
2
w
3
f
C
3
w
3
x
j
Figure 2: (Left) This figure describes how in a standard bag-of-words model in which two features x
i
and x
j
are assigned to
the word w
3
and their differences are neglected while is possible. (Right) to pull out their differences after being assigned to
w
3
using the f
C
w
hyperplanes. These differences are later used for constructing a feature descriptor.
Table 1: Confusion Matrix for max operator (Accuracy 94%) using a vocabulary of size 1500.
1 2 3 4 5 6 7 8 9
1-Cow 12 0 0 0 0 0 0 3 0
2-Plane 0 15 0 0 0 0 0 0 0
3-Face 0 0 15 0 0 0 0 0 0
4-Car 0 0 0 15 0 0 0 0 0
5-Bike 0 0 0 0 15 0 0 0 0
6-Book 0 0 0 1 0 14 0 0 0
7-Sign 0 0 0 0 0 2 13 0 0
8-Sheep 1 0 0 0 0 0 0 14 0
9-Chair 1 0 0 0 0 0 0 0 14
Table 2: Confusion matrix for bag-of-words histogram (Accuracy 88%) using a vocabulary of size 1500.
1 2 3 4 5 6 7 8 9
1-Cow 13 0 0 0 0 0 0 2 0
2-Plane 0 15 0 0 0 0 0 0 0
3-Face 0 0 14 0 0 0 1 0 0
4-Car 0 0 0 14 0 0 1 0 0
5-Bike 0 0 0 0 15 0 0 0 0
6-Book 0 0 0 0 0 15 0 0 0
7-Sign 1 0 0 0 0 1 11 0 2
8-Sheep 2 0 0 0 0 0 0 13 0
9-Chair 0 0 0 0 3 0 2 0 10
3 METHODOLOGY
To measure the quality of the features assigned
to the different visual words lets assume that
{(x
1
, y
1
), ..., (x
n
, y
n
)} is a set of labeled features ex-
tracted from an image dataset with y
i
∈ {C
1
, ..., C
M
}
and D is an already trained vocabulary with N words.
The goal here is to train class specific classifiers, f
C
w
,
for the features that have been assigned to each visual
word. These classifiers are trained by selecting as-
signed features and creating a binary labeling by as-
signing features with y
i
= C to 1 and others to −1. In
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
190

this work our classifier is formulated as a linear re-
gression and it is defined as
f
C
w
= argmin
f
1
n
∑
x
|x
T
f − ¯y
C
|
+ λ| f |
2
. (3)
Here the x is chosen only from the features with
l(x) = w and ¯y
C
represents the binary labeling of these
features with respect to class C. The value of λ can
be obtained through cross-validation. Figure 2 shows
how more detailed information can be extracted from
the features that were treated equally by the bag-of-
words model. In this figure we can see that the two
features x
i
and x
j
are both labeled as w
3
have a differ-
ent behavior with respect to the hyperplanes f
C
1
w
3
, f
C
2
w
3
and f
C
3
w
3
which encode class properties in this section
of the space. To estimate the quality of a feature (the
likelihood of belonging to class C while assigned to
the word w), we use the logistic function
P
C
w
(x) =
1
1+ exp(−a(x
T
f
C
w
))
. (4)
For any set of features extracted from an image we
wish to build a descriptor based on their quality rather
than their visual word quantity. To do so, the features
are initially labeled using a vocabulary D. As previ-
ously argued each word in D captures a certain struc-
ture on the image. Hence, the role of P
C
w
(x
i
) function,
Eq. 4, is to measure the quality the discovered struc-
tures assigned to the word w with respect to class C.
This is a one dimensional measurement correspond-
ing to the models confidence. To that end it is possi-
ble construct a (N.M) dimensional descriptor D, with
N being the size of the vocabulary and M the number
of classes. Each dimension of this vector corresponds
to responses associated with a certain word (w
n
) with
respect to a certain class (C
m
). The question here is
how one can summarize these values into a number
that can capture the qualitative properties of features
seen in the image. Here we analyze the max descrip-
tor defined as
D
max
[i] = max
P
C
m
w
n
(x) : x ∈ I, l(x) = w
n
, (5)
which focuses on pooling the features with the high-
est likelihood rather than relying on the quantitative
properties of the their labeling. This can also be seen
as a feature selection problem, where the highest like-
lihood features are used for describing the image. The
max pooling is dependent on the accuracy of P
C
w
(x)
functions and increasing their accuracy will result in
a better description of the image. Similar to max de-
scriptor it is also possible to define the mean descrip-
tor D
mean
by replacing the max operation in Eq. 5
with mean operation.
4 EXPERIMENTS
In this section we compare the performance of the
proposed descriptor with the standard bag-of-words
histogram as the baseline. For both descriptors the
same vocabulary is used for summarizing the image.
To compare the performance we use vocabularies of
different sizes, since the size of a vocabulary is usu-
ally associated with the performance of the bag-of-
words histogram as a descriptor. In this experiment
the sift features (Vedaldi and Fulkerson, 2008) as base
features which are densely sampled from an image
pyramid and the image pyramid consists of eight lev-
els. The visual vocabularies are computed using stan-
dard k-means algorithm.
The experiments of this paper are conducted on
the MSRCv2 dataset (Winn et al., 2005). Although
this dataset is relatively small compared to other
datasets, it is considered as a challenging and difficult
dataset due to its high intra-class variability. In this
work we have followed the experiments setup used in
(Zhang and Chen, 2009; Morioka and Satoh, 2010),
with a denser sampling of sift features from different
scale levels. In our experiment nine of fifteen classes
are chosen ({ cow, airplanes, faces, cars, bikes, books,
signs, sheep, chairs}) with each class containing 30
images. For each experiment, the images of each class
were randomly divided into 15 training and 15 test-
ing images and no background was removed from the
images. The random sampling of training and test-
ing images were repeated 5 times. In our experiment
a one-against-all linear SVM (Chang and Lin, 2011)
was learnt for each class and the test images were
classified to the class with the highest probability.
To compare the performance of bag-of-words his-
togram with the proposed descriptor, visual vocabu-
laries with different sizes {50, 100, 200, 300, 400,
500, 1000, 1500} were computed over the training
subset using standard k-means algorithm. Figure 3
shows how the max descriptor (Eq. 5) is either out
performing or has a comparable accuracy to the bag-
of-words histogram in all vocabulary sizes. Tables 1
and 2 compare the confusion matrices of best classifi-
cations using a vocabulary of size 1500 for both max
descriptor and bag-of-words histogram. These tables
show how a richer descriptor is obtained when quality
of word are measured rather in oppose to their quan-
tity. We also evaluate the mean summarizing, which
is created by replacing the max operator in Eq. 5 with
the mean operator. As it can be seen in figure 3 the
mean descriptor has a very low performance when
the size of the vocabulary is low. This low accuracy is
due to the fact that the background was not removed
and lots of low quality instances of visual words were
QualitativeVocabularybasedDescriptor
191

0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
0 200 400 600 800 1000 1200 1400
Accuracy
Vocabulary Size
Histogram
Max Descriptor
Mean Descriptor
Figure 3: This figure compares the average performance of different descriptors with respect to the size of the vocabulary.
Here the max descriptor shows a better performance than bag-of-words histogram in almost all vocabulary sizes. Since no
background was removed from the test images the performance of the mean descriptor is expected to be low when the size of
the vocabulary is small. It can be seen how with larger vocabulary sizes, where more sophisticated appear in the vocabulary,
the mean descriptor out performs the bag-of-words histogram by a large margin.
found in the test image. Meanwhile with increase of
the size of the vocabulary the accuracy of this descrip-
tor significantly increases. This increase is due to the
fact that with increase of the size of vocabulary more
sophisticated words are discovered.
The MSRCv2 has appeared in a variety of re-
searches as a testing platform for different algorithms.
Among those one can focus on (Zhang and Chen,
2009; Morioka and Satoh, 2010) where the authors
tend to build a more sophisticated vocabulary by
spatially combining local features into higher order
features. These higher order features either con-
sist of several visual words couples together (Zhang
and Chen, 2009) or are joint feature representations
(Morioka and Satoh, 2010). The difference between
their approach and the proposed approach is that fact
that our approach summarises the images using first
order statistics in a more discriminative manner. Ta-
ble 3 shows how our method is out preforming the
previously published methods on this dataset.
5 CONCLUSIONS
We proposed a method that looks at the bag-of-words
models from a qualitative perspective rather than a
quantitative perspective. We experimentally show
that by describing images based on the quality of the
Table 3: Comparison between the classification rates ob-
tained by the proposed method and the previously published
methods on MSRCv2 dataset.
Method Acc %
2
nd
order spatial (Zhang and Chen, 2009) 78.3± 2.6%
10
th
order spatial (Zhang and Chen, 2009) 80.4± 2.5%
QPC (Morioka and Satoh, 2010) 81.8± 3.4%
LPC (Morioka and Satoh, 2010) 83.9± 2.9%
Multi-Scale BOW 85.3± 3.2%
Mean Descriptor 88.5± 4.3%
Max Descriptor 89.2± 3.9%
visual words provides a better descriptor for image
classification. In this work a series of linear regres-
sions were used for measuring the quality of the local
features assigned to different visual words. Although
the performance of these local regressions are not dis-
cussed in this paper it is clear that their performance
has a direct effect on the resulting descriptor. This
facts provides a new tool for improving the perfor-
mance of vocabulary based models. Studies such as
(Afkham et al., 2012) have shown that it is possible to
improve the performance of these local classifiers by
combining severallocal features. Due to the complex-
ity, combining our method with such local classifiers
is left to the future works of this paper.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
192

ACKNOWLEDGEMENTS
This work was supported by The Swedish Foundation
for Strategic Research in the project “Wearable Visual
Information Systems”.
REFERENCES
Afkham, H. M., Carlsson, S., and Sullivan, J. (2012). Im-
proving feature level likelihoods using cloud features.
In ICPRAM (2), pages 431–437.
Bouachir, W., Kardouchi, M., and Belacel, N. (2009). Im-
proving bag of visual words image retrieval: A fuzzy
weighting scheme for efficient indexation. In Pro-
ceedings of the 2009 Fifth International Conference
on Signal Image Technology and Internet Based Sys-
tems, SITIS ’09, pages 215–220, Washington, DC,
USA. IEEE Computer Society.
Boureau, Y.-L., Ponce, J., and LeCun, Y. (2010). A theoret-
ical analysis of feature pooling in visual recognition.
In ICML, pages 111–118.
Chang, C.-C. and Lin, C.-J. (2011). LIBSVM:
A library for support vector machines. ACM
Transactions on Intelligent Systems and Tech-
nology, 2:27:1–27:27. Software available at
http://www.csie.ntu.edu.tw/ cjlin/libsvm.
Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y.
(2009). What is the best multi-stage architecture for
object recognition? In Proc. International Conference
on Computer Vision (ICCV’09). IEEE.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
bags of features: Spatial pyramid matching for rec-
ognizing natural scene categories. In Proceedings
of the 2006 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition - Volume 2,
CVPR ’06, pages 2169–2178, Washington, DC, USA.
IEEE Computer Society.
Morioka, N. and Satoh, S. (2010). Building compact local
pairwise codebook with joint feature space clustering.
In Proceedings of the 11th European conference on
Computer vision: Part I, ECCV’10, pages 692–705,
Berlin, Heidelberg. Springer-Verlag.
Russell, B. C., Efros, A. A., Sivic, J., Freeman, W. T.,
and Zisserman, A. (2006). Using multiple segmen-
tations to discover objects and their extent in image
collections. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition.
Savarese, S., Winn, J., and Criminisi, A. (2006). Discrimi-
native object class models of appearance and shape by
correlatons. In Proceedings of the 2006 IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition - Volume 2, CVPR ’06, pages
2033–2040, Washington, DC, USA. IEEE Computer
Society.
Sivic, J., Russell, B. C., Efros, A. A., Zisserman, A., and
Freeman, W. T. (2005). Discovering object categories
in image collections. In Proceedings of the Interna-
tional Conference on Computer Vision.
Vedaldi, A. and Fulkerson, B. (2008). VLFeat: An open
and portable library of computer vision algorithms.
http://www.vlfeat.org/.
Wang, X., Mohanty, N., and Mccallum, A. (2005). Group
and topic discovery from relations and text. In KDD
Workshop on Link Discovery: Issues, Approaches and
Applications (LinkKDD).
Winn, J., Criminisi, A., and Minka, T. (2005). Object cat-
egorization by learned universal visual dictionary. In
Proceedings of the Tenth IEEE International Confer-
ence on Computer Vision - Volume 2, ICCV ’05, pages
1800–1807, Washington, DC, USA. IEEE Computer
Society.
Zhang, Y. and Chen, T. (2009). Efficient kernels for iden-
tifying unbounded-order spatial features. In CVPR,
pages 1762–1769.
QualitativeVocabularybasedDescriptor
193
