
Nonlinearity Reduction of Manifolds using Gaussian Blur for
Handshape Recognition based on Multi-Dimensional Grids
Mohamed Farouk
1
, Alistair Sutherland
2
and Amin Shokry
3
1,2
School of computing, Dublin City University, Dublin, Ireland
3
Computer & Systems Eng. Dept., Faculty of Engineering, Alexandria University, Alex, Egypt
Keywords: Principal Component Analysis, Gaussian Blurring, Multi-dimensional Grids, Multi-stage Hierarchy.
Abstract: This paper presents a hand-shape recognition algorithm based on using multi-dimensional grids (MDGs) to
divide the feature space of a set of hand images. Principal Component Analysis (PCA) is used as a feature
extraction and dimensionality reduction method to generate eigenspaces from example images. Images are
blurred by convolving with a Gaussian kernel as a low pass filter. Image blurring is used to reduce the non-
linearity in the manifolds within the eigenspaces where MDG structure can be used to divide the spaces
linearly. The algorithm is invariant to linear transformations like rotation and translation. Computer
generated images for different hand-shapes in Irish Sign Language are used in testing. Experimental results
show accuracy and performance of the proposed algorithm in terms of blurring level and MDG size.
1 INTRODUCTION
Gestures are a useful way of communication
between people to express what they want to say in
everyday life. Hand shape recognition for gestures
provides a natural interaction between humans and
computers. The key problem in gesture interaction is
how to make hand gestures understood by
computers. Automatic sign language recognition is
one of the applications in that area. Signs can be
considered as continuous sequence of postures with
different hand shapes and positions within a small
interval of time under a certain gesture grammar.
Gesture recognition approaches can be divided
into glove-based and vision-based. The first
approach uses electronic gloves to gather the
information about the hand shape and its position via
a set of sensors. Data gloves give good information.
However, they are expensive and bring
cumbersomeness to the users. On the other hand,
vision-based methods use only a camera to capture
the hand shape in a natural way of interaction. There
are two categories of vision-based systems either a
model-based or appearance-based methods.
Model-based methods depend on the 3D
kinematics of a hand model. They provide a rich
description for the hand shapes. However, it is a
computationally expensive process. Appearance-
based methods depend on extracting the features of
the images from the input video frames. Generally
these methods have the advantage of real time
performance. There are different techniques used to
build classifiers in this category. PCA is one of these
techniques. PCA can be used as a feature extraction
and dimensionality reduction method. The data are
projected into the eigenspace defined by the
principal axes calculated from the covariance matrix
of the training data. In (Huang and Hu, 2010) PCA
is used to reduce the dimensionality of Gabor
filtered images where the SVM method is adopted to
carry out the recognition task. In (Shahbudin and
Hussain, 2010) the PCA technique is applied to
extract features from human shape silhouettes. In
(Gastaldi and Pareschi, 2005
) the recognition
process uses a statistical approach based on Hidden
Markov Models after using PCA for dimensionality
reduction and feature extraction from the input
sequence.
2 RELATED WORK
An “image pyramid” is a data structure that stores
different versions of an image at different scales.
These versions are decreased in resolution in regular
steps. The pyramid algorithm consists of a
convolution process between a target image and the
sequence of images that are stored in the different
303
Farouk M., Sutherland A. and Shokry A. (2013).
Nonlinearity Reduction of Manifolds using Gaussian Blur for Handshape Recognition based on Multi-Dimensional Grids.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 303-307
DOI: 10.5220/0004267103030307
Copyright
c
SciTePress

levels of the pyramid. It can be used in image
analysis to do pattern matching. This process is
concerned with finding a particular target pattern
that may exist at any scale within an image. (Adelson
and Anderson, 1984). The same structure is well
suited for a variety of other image processing tasks.
In (Yang and Yu, 2009
) an extension of the spatial
pyramid matching approach is proposed, which
computes a spatial-pyramid image representation
based on sparse codes. In (Zhang and Chai, 2011)
mask pyramids are used to build an algorithm that
localizes the selection process.
The multi-dimensional grid is a methodology
that can be used to cluster data into groups of similar
objects. The MDG divides the feature space into
hyper-rectangular blocks so that it organizes the
feature space surrounding the patterns and not the
patterns themselves (Schikuta ,1996). In (Amini and
Wah, 2011) grid clustering is used as a natural
choice for infinite data streams which are mapped to
finite grid cells where the synopsis information for
data streams is contained in the grid cells.
The convolution of a kernel described by a
Gaussian function with the pixels of an image is
commonly called a Gaussian blur. This process is
usually used as a low pass filter, to filter images
from noise that is inherent in the physical process of
acquisition. In (I. Stainvas and N. Intrator, 2000)
feed forward networks are trained on original as well
as Gaussian-blurred images to achieve higher
robustness to different blur operators. In (Z. Chen
and S. Nie, 2008) a Gaussian Blur filter is used to
help in the automatic segmentation of liver from CT
images by connecting isolated pixel clusters in the
extracted liver part from the binary image.
3 PROPOSED ALGORITHM
The proposed algorithm depends on data pyramids,
multi-dimensional grids, and image blurring to build
a classifier that uses manifolds in a Principal
Component Analysis space. The algorithm follows
the idea of data pyramids in that each level, in a
multistage hierarchy, consists of a different
eigenspace instead of using different image
resolution as described before. The different
eigenspaces at the different levels of the proposed
multistage hierarchy help in analysing an incoming
object from one level to another. The proposed
algorithm explores the effect of Gaussian blurring on
reducing the nonlinearity in the manifolds. Multi-
dimensional grids are used to divide the space
linearly into cells that cluster the data into small
groups of similar objects. A new incoming object is
labeled according to the objects within the cell, into
which it is projected. Our experimental results show
that blurring can affect the choice of the best grid
size in order to get the highest accuracy.
3.1 Linearizing the Manifolds by
Gaussian Blurring
The proposed algorithms explore the effect of image
blurring using Gaussian Kernels on the classification
process. To get a good generalization for the
problem, both the incoming object and the training
sample are blurred by the same Gaussian kernel. As
blurring has the effect of removing small changes
between objects, the classification process of a new
incoming object will be easier. At a certain blurring
level, it is possible to classify the incoming object
using the suitable distance measure.
To illustrate our algorithm, a dataset of computer
generated images of a human arm and hand are used.
The dataset consists of 20 different hand shapes
from the Irish Sign Language alphabet. To build a
“translation manifold”, PCA is applied to a set of
images that represent a hand-shape, which is
translated from -5 to +5 pixels in the horizontal and
vertical direction forming 121 objects as shown in
Figure 1. Image blurring reduces the nonlinearity of
the translation manifolds and makes the manifolds
more flat. It has the effect of grouping objects
together and so the feature space of the data starts to
shrink as it removes the small changes between
objects. The manifolds get closer together
numerically but they become more linear and more
parallel. Flattening the manifolds makes the
manifolds more linearly separated in the space.
Figure 1 shows two neighbouring manifolds before
and after blurring (using the 1
st
and 2
nd
eigenvectors).
Figure 1: The effect of blurring on separating the
Manifolds.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
304

3.2 Different PCA Spaces
Different PCA spaces are generated to fit the
requirements of each level in the multistage
hierarchy. To extract the effect of rotation on a hand
shape, PCA is applied to images of a certain shape at
different rotation angles. The resulting eigenspace
contains a “rotation manifold”. And to differentiate
between different hand shapes, PCA is applied to
images for the 20 shapes at the same rotation angle.
The resulting eigenspace contains a “shape
manifold”. The order of the shapes within a shape
manifold is quite interesting. Figure 2 illustrates how
PCA extracts the underlying structure within the
data. Hand shapes which are close together in the
manifold have similar images. The sequence starts
with “O” which is a closed compact shape and ends
with “L” which is a broad open shape.
Figure 2: Computer generated images for 20 Shapes in the
Irish Sign Language in the Sequence for a Shape
Manifold.
3.3 The Multistage Hierarchy
To be invariant to linear transformations like
translation and rotation, a large number of
translation manifolds are generated for the different
hand shapes at different rotations for the signer arm.
As the range of angles to be represented increases,
the number of manifolds increases and consequently
the space of manifolds to be searched becomes
larger. It is computationally expensive to project the
incoming object into all these different manifolds
where each manifold has its own set of eigenvectors.
In order to solve this problem, a multistage
hierarchical structure is used to reduce the search
space at each stage to find the right manifold to
search in and hence decide the shape, rotation, and
translation position of an incoming sign object.
The proposed algorithm uses multi-dimensional
grids that divide these different spaces into cells.
The objects within each cell can give enough
information to classify a new incoming object in an
accurate and efficient way. The MDG structure can
be built using the dominant set of eigenvectors. The
grid divides each direction of the space into equal
intervals based on the range of feature values of the
objects that is used to build that eigenspace.
At a certain blurring level, the nonlinearity of the
manifolds is reduced to a level that helps in getting
the best grid structure. The sides of the hyper-blocks
within this grid actually represent the linear decision
boundaries that split the objects into different
groups. The algorithm follows a hierarchical strategy
to classify the incoming object in an efficient and
accurate way as it is described in Figure 3.
Figure 3: Multistage Hierarchy Using MDGs.
3.3.1 Estimating the Rotation Angle
At a certain level of blurring, the dominant effect
will be the rotation of the signer arm. So it is
possible at the first stage to estimate a range of
rotation angles for the incoming object. Estimating
the range of rotation angles is done at the first stage
of the hierarchy, as rotation has the highest variation
in the data.
In Stage 1.A, each cell in the MDG is labelled
according to the minimum and maximum rotation
angles for the objects it holds. In order to classify a
new incoming object, it is blurred to the same level
of the MDG and projected into it. According to the
label of the cell it is projected into, estimation for the
range of angles for that object is obtained. A rotation
manifold for sign “H”, as the most centrally located
shape, is used to compute the eigenvectors and cells
of the MDG. Every fifth image is used in order to be
able to compute the covariance matrix. However,
this does not provide enough data to fill all the cells
of the MDG. So other objects from different shapes
NonlinearityReductionofManifoldsusingGaussianBlurforHandshapeRecognitionbasedonMulti-DimensionalGrids
305
at the same rotations are projected into the space to
fill in some of the empty cells. This improves the
accuracy of the proposed algorithm as projecting an
object into an empty cell leads to misestimating its
rotation angle and hence may cause a
misclassification for the shape in the next stage. The
size of the MDG, in terms of the number of
eigenvectors and the number of cells in each
direction, has an effect on the number of objects
within the cells and hence the range of angles within
them. The blurring level also has an effect on the
distribution of objects within the grid as it makes the
manifolds more flat and reduces the distances
between objects. A study about these factors and the
effect on both accuracy and performance is given in
the experimental results section.
In Stage 1.B, a sub-stage is applied by projecting
the incoming object into a smaller MDG. The goal
of this sub-stage is to increase the precision by
estimating a narrower range of angles while
preserving the accuracy. Smaller MDGs are
constructed using the 6 images from the training set
representing the range of angles intermediate
between the angles used for the bigger grid. The new
incoming object is projected again into one of these
smaller MDGs based on the range of angles that has
been estimated from the first bigger MDG at Stage
1.A where the range of angles estimated from this
smaller MDG is passed to stage 2.
3.3.2 Shape Classification
At the second stage shape manifolds are used to
classify the shape of an incoming object. This stage
is carried out only for objects with the estimated
range of rotation angles obtained at the first stage.
MDGs are constructed using shape manifolds for
each pair of angles. Each eigenspace is constructed
for all shapes and translation at a pair of angles in
order to be able to compute the covariance matrix.
According to the range of angles that has been
estimated by the first stage, a new incoming object is
projected into a number of MDGs in the second
stage which cover that range. The smaller the
number of angles from the first stage to be searched
in, the fewer MDGs will be searched and the more
speed is gained.
3.3.3 Final Classification
A final third stage is done using a nearest neighbour
search. According to the cell, which the incoming
object is projected into in the second stage, a nearest
neighbour search is done in the third stage for the
objects within that cell. If more than one MDG is
used to cover the estimated range of angles from the
first stage, the nearest neighbour object over all
MDGs from the second stage will be used to classify
the new incoming object to give a final decision
about its shape, rotation, and translation position.
Manhattan distance is used as a distance measure in
this stage. The number of eigenvectors, which are
used to compute the distance measure, will affect the
accuracy of the algorithm as will be discussed later
in the experimental results.
4 EXPERIMENTAL RESULTS
All the experiments are done on Intel Core 2 Duo
CPU @ 2.66GHz, 2.00 GB of RAM. Blurred images
are created using a two-dimensional Gaussian low-
pass filter of size [6,6] and with standard deviation
equals to 10. The results are based on a data sample
of 14520 objects. The sample represents the 20
shapes at the first 6 angles from +90 degrees to +180
degrees. The test set is created by 1 degree rotation
clock wise from the original set, where images in the
original set are 2 degrees a part.
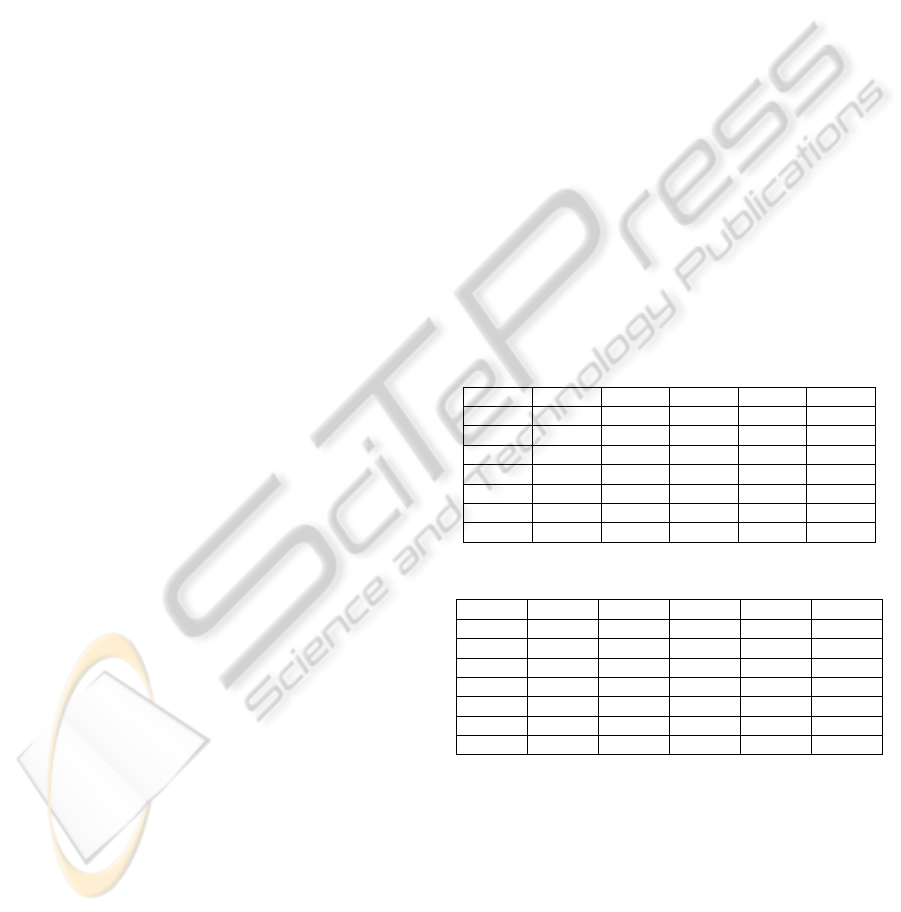
Table 1: Maximum range of angles at stage 1.A.
10^2 10^3 5^4 7^4 10^4
B0
21 11 11 11 11
B2
21 16 11 11 11
B4
16 11 11 11
6
B6
16 11 11
6 6
B8
16 11 11
6 6
B10
16 11 11 11
6
B12
16 11 11 11
6
Table 2: Accuracy at stage 1.A.
10^2 10^3 5^4 7^4 10^4
B0
98.2 90.8 94.9 94.5 85.8
B2
98.6 94.1 94.7 93.2 84.9
B4
99.0 92.9 94.2 92.6
82.8
B6
98.9 91.9 95.3
91.2 81.3
B8
99.0 93.1 92.9
91.1 80.5
B10
98.0 89.7 87.7 82.0
77.9
B12
98.5 90.1 93.8 79.45
76.0
The size of the MDG in Stage 1.A should
preserve the precision of the range of angles within
all nonempty cells to a maximum of 6 different
rotations and at a high level of accuracy in
estimating the rotation angle as well. Different
structures for the MDG in terms of the number of
eigenvectors and the divisions along each direction
are tested using different blurring levels. Table (1)
shows the maximum number of angles within the
cells using five different structures for the MDG and
at different blurring levels as well, where Table (2)
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
306

shows the accuracy of the estimation process of the
rotation angle at the same structures.
From the previous two tables, increasing the
MDG size increases the number of cells and
decreases the range of angles within them as fewer
objects are held by each cell. However, this reduces
the accuracy of the process as more empty cells are
generated within the MDG and the rotation angle of
an incoming object can be misestimated in that case.
From the previous tables, the size of [7x7x7x7] with
a blurring level of 6 is the best for constructing the
MDG in stage 1.A where all the nonempty cells
have a maximum of 6 different angles and an
accuracy of 91.2% in estimating the rotation angle.
To reach a precision of 4 rotation angles within the
nonempty cells in stage 1.B, the MDG of size
[7x7x7x7] is used under blurring level 6. The
accuracy of estimating the rotation angle at this size
reached 94.2%.
Based on using MDGs of size [4x4x4] and
blurring level 6 in stage 2, the proposed algorithm
reached 97.2% in detecting different hand shapes
using 17 eigenvectors for the distance measure in
stage 3, where each objects needs 0.064 sec to be
classified. Figure 4 shows the effect of using
different numbers of eigenvectors in the third stage
on the accuracy of shape detection.
Figure 4: Accuracy versus different number of eigen-
vectors.
5 CONCLUSIONS
Gaussian blur can be used to reduce the nonlinearity
of the manifolds in PCA spaces. MDGs can divide
the space linearly for a set of blurred images into
cells that hold information from a training set of
computer-generated objects. At the best blurring
level and the best number of cells in the MDGs, the
proposed algorithm reached an accuracy of 97.2%
where each object needs 0.064 sec to be classified.
REFERENCES
D. Huang, W. Hu, S. Chang, and M. Chen, 2010. Gabor
filter-based hand-pose angle estimation for hand
gesture recognition under varying illumination. Expert
Systems With Applications, pp.6031–6042.
Shahrani Shahbudin, Aini Hussain, Hafizah Hussain,
Salina A.Samad, and Nooritawati Md. Tahir, 2010
Analysis of PCA Based Feature Vectors for SVM
Posture. 6th International Conference on
Classification. Signal Processing and Its Applications,
pp.1 – 6.
Giulia Gastaldi, Alessandro Pareschi, Silvio P. Sabatini,
Fabio Solari and Giacomo M. Bisio, 2005. A man-
machine communication system based on the visual
analysis of dynamic gestures. International
Conference on Image Processing, pp.397-400.
E. H. Adelson, C. H. Anderson, J. R. Bergen, P. J. Burt,
and J. M.Ogden, 1984. Pyramid methods in image
processing. RCA Engineer,pp. 33-41.
J. Yang, K. Yu, Y. Gong, and T. Huang, 2009. Linear
spatial pyramid matching using sparse coding for
image classification, Computer Vision and Pattern
Recognition, pp. 1794-1801.
David C. Zhang, Sek Chai, and Gooitzen Van der Wal,
2011. Method of Image Fusion and Enhancement
Using Mask Pyramid, 14th International Conference
on Information Fusion, pp. 1-8.
E. Schikuta, 1996. Grid-Clustering: A Fast Hierarchical
Clustering Method for Very Large Data Sets. 13th Int.
Conf. On Pattern Recognition, pp. 101-105.
Amineh Amini, Teh Ying Wah, Mahmoud Reza Saybani,
and Saeed Reza Aghabozorgi Sahaf Yazdi, 2011. A
study of density-grid based clustering algorithms on
data streams. 8th International Conference on Fuzzy
Systems and Knowledge Discovery, pp.1652-1656.
Inna Stainvas and Nathan Intrator, 2000. Blurred face
recognition via a hybrid network architecture. 15th
International Conference on Pattern Recognition, pp.
805-808.
Z. Chen, S. Nie, L. Qian, and J. Xu, 2008. Automatic liver
segmentation method based on a gaussian blurring
technique for CT images. The 2nd International
Conference on Bioinformatics and Biomedical
ngineering, pp. 2516 - 2518.
NonlinearityReductionofManifoldsusingGaussianBlurforHandshapeRecognitionbasedonMulti-DimensionalGrids
307
