
MolMap
Visualizing Molecule Libraries as Topographic Maps
Martin Gronemann
1
, Michael J
¨
unger
1
, Nils Kriege
2
and Petra Mutzel
2
1
Institut f
¨
ur Informatik, Universit
¨
at zu K
¨
oln, K
¨
oln, Germany
2
Dept. of Computer Science, Technische Universit
¨
at Dortmund, Dortmund, Germany
Keywords:
Graph Drawing, Clustered Graphs, Topographic Maps, Drug Discovery, Molecule Libraries.
Abstract:
We present a new application for graph drawing and visualization in the context of drug discovery. Combining
the scaffold-based cluster hierarchy with molecular similarity graphs — both standard concepts in cheminfor-
matics — allows one to get new insights for analyzing large molecule libraries. The derived clustered graphs
represent different aspects of structural similarity. We suggest visualizing them as topographic maps. Since
the cluster hierarchy does not reflect the underlying graph structure as in (Gronemann and J
¨
unger, 2012), we
suggest a new partitioning algorithm that takes the edges of the graph into account. Experiments show that the
new algorithm leads to significant improvements in terms of the edge lengths in the obtained drawings.
1 INTRODUCTION
Drug discovery is a tedious and expensive process that
typically involves the experimental evaluation of large
compound libraries by high-throughput screening in
order to identify promising small molecules that bind
to a specific biological target. These compounds may
serve as a starting point for chemical modifications,
e.g., in order to reduce side effects or to improve
potency. A guiding principle during this process is
to elucidate and exploit the relationship between the
structure of a molecule and its biological properties.
In the course of the drug discovery process typi-
cally structural information on compounds as well as
experimental results are generated. Supporting the
drug discovery process based on this data by ade-
quate computational methods like, e.g., largely auto-
mated data mining algorithms, is a fundamental task
in cheminformatics (Brown, 2009). However, only
recently several sophisticated visual analysis tools for
this domain have been developed (Wetzel et al., 2009;
Klein et al., 2012; Lounkine et al., 2010; Strobelt
et al., 2012; Herhaus et al., 2009) with the aim to
allow the user to explore the chemical space and
make decisions based on his expert knowledge. These
tools often represent sets of molecules and their struc-
tural relations by means of graphs, and they rely on
graph drawing techniques for visualization. Since
structural relations are rather complex, different ap-
proaches have been developed, some of which orga-
nize molecules in a tree-like hierarchy while others
are based on pairwise similarities. The complexity of
structural relations, the amount of data and the differ-
ent perspectives chemists from different branches of
chemistry may have makes it difficult to find an ap-
proach that satisfies all needs.
Irwin recently summarized the problem as fol-
lows: “In principle, one would like to be able to or-
ganize and browse large chemical datasets [. . . ] as
easily as one can today browse maps on the inter-
net.” (Irwin, 2009) This comparison gives the im-
petus for our approach to represent molecule sets
by clustered graphs, which are then visualized as
topographic maps based on a method recently pro-
posed (Gronemann and J
¨
unger, 2012). The use of
clustered graphs allows us to model different aspects
of structural similarity between compounds in a single
graph and to visualize them in one picture in which
similar molecules appear close to each other. Clus-
tered graphs have not yet been applied to visualize
chemical compounds, the most likely reason is that
drawing them is difficult. This is caused by the re-
quirement to generate an appealing drawing of the
underlying graph that simultaneously represents the
hierarchy of nested subsets of its nodes. The issue
becomes especially challenging when the cluster hi-
erarchy does not reflect the “natural” clusters of the
underlying graph. This problem arises with our rep-
resentation of molecular data sets by clustered graphs
and was not addressed in (Gronemann and J
¨
unger,
515
Gronemann M., Jünger M., Kriege N. and Mutzel P..
MolMap - Visualizing Molecule Libraries as Topographic Maps.
DOI: 10.5220/0004267205150524
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (IVAPP-2013), pages 515-524
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

2012). Therefore we develop a new partitioning pro-
cedure that exploits the degrees of freedom in the al-
gorithm with the goal to obtain shorter edges. In order
to meet the requirements of the application domain,
our procedure also supports the display of structural
formulae of compounds and the superimposition of
a heat map that allows the representation of property
values.
2 RELATED WORK
A straight-forward and wide-spread approach to
browse compound datasets are molecular spread-
sheets depicting compounds and their properties in
table form. Recently several more sophisticated tools
for the visualization of compound sets have been de-
veloped. Many of these represent chemical com-
pounds by means of graphs:
In (Wawer et al., 2008) the concept of ‘Network-
like Similarity Graphs’ was introduced to study
structure-activity relationships of small molecules.
Here, compounds are represented by nodes and two
nodes are connected by an edge if their compounds
exceed a certain similarity threshold. These graphs
are then visualized using a force-directed layout algo-
rithm (Fruchterman and Reingold, 1991). In addition,
similarities are used to derive a hierarchical cluster-
ing of all nodes. However, for visualization only a
single clustering is selected instead of displaying the
full hierarchy. The approach was implemented by the
open-source application SARANEA (Lounkine et al.,
2010) based on the framework JUNG
1
. A different
application, also based on pairwise molecular simi-
larities, is HiTSEE (Strobelt et al., 2012). This tool
maps compounds on the plane trying to preserve dis-
tances derived from similarities by Multidimensional
Scaling (MDS).
Several concepts to organize compounds via hi-
erarchical classification schemes have been pro-
posed (Schuffenhauer and Varin, 2011). These are,
e.g., based on clustering algorithms or on domain spe-
cific methods based on rules incorporating chemical
knowledge. An approach of the second category is the
so-called scaffold tree (Schuffenhauer et al., 2007) on
which the visual analysis tool Scaffold Hunter (Wet-
zel et al., 2009; Klein et al., 2012) is based. For
visualization, a radial style tree drawing algorithm
is used. The tool MolWind (Herhaus et al., 2009)
is also based on the scaffold tree concept, but uses
NASA’s World Wind engine to map scaffolds to a vir-
tual globe. While MolWind is not directly related
1
http://jung.sourceforge.net
to graph drawing, we take up the MolWind idea to
map chemical information to intuitively understand-
able geographic representations, and realize it in the
realm of clustered graph drawing.
While clustered graph drawing is a lively research
topic in graph drawing (Sugiyama and Misue, 1991;
Huang and Eades, 1998) (see, e.g., in GDEA
2
), only
few approaches exist for drawing clustered graphs as
maps. Gansner et al. have suggested the use of ge-
ographic maps for enhancing clusters and visualiz-
ing similarities (Gansner et al., 2009; Gansner et al.,
2010). They first compute a partition of the nodes by
applying a cluster algorithm, then use a force-directed
method or MDS to compute a layout, and finally use
both to create a colored map. The combination of
the layout and clustering methods used for generating
the map, plays an important role regarding the visual
shape of the clusters in the final layout. In order to
obtain a map where the countries form compact ar-
eas, requires that the result produced by the layout
algorithm matches the partitioning of the clustering
step. Otherwise, the partitions are visually scattered,
this problem is referred to as fragmentation.
An alternative approach for visualizing hierarchi-
cally clustered graphs as topographic maps has been
suggested recently in (Gronemann and J
¨
unger, 2012).
Topographic maps have a long history in information
visualization. Mostly used for visualizing point dis-
tributions, they offer a natural way to explore data.
In (Fabrikant et al., 2010) the effect of using to-
pographic maps as metaphor is studied. They confirm
the usage of elevation levels as an effective way to en-
code similarities. Gronemann and J
¨
unger propose to
represent the complete hierarchy of a clustered graph
by elevation levels. The elevation model is defined
such that nodes in different subtrees are separated by
a valley. In other words, nodes in the same cluster
are placed together on a plateau. This simple idea
requires that the layout algorithm generates compact
areas for all clusters.
By using a treemap approach for the layout the
problem of fragmentation is avoided. Several meth-
ods for generating treemaps exist in the literature.
Starting with the work of (Johnson and Shneiderman,
1991), where a hierarchy is mapped on a space fill-
ing curve, most algorithms are based on a rectan-
gular subdivision scheme. A good overview over
the vast amount of treemap techniques can be found
in (Schulz, 2011).
2
Graph Drawing E-Print Archive,
http://gdea.informatik.unikoeln.de/
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
516

3 COMPOUND LIBRARIES
AND CLUSTERED GRAPHS
A clustered graph is a tuple (G,T ), where G = (V,E)
is graph and T = (V
T
,E
T
) is a rooted tree such that
the leaves of T are the nodes in V . Each inner node
v of T corresponds to a cluster of G comprising all
leaves of the subtree rooted at v. Therefore the inner
nodes of T are called cluster nodes, T is referred to as
cluster tree and defines a hierarchy of nested subsets
of V .
Approaches to explore chemical compound li-
braries typically allow the user to navigate between
regions of molecules with a similar structure. We
combine two orthogonal concepts from cheminfor-
matics to derive clustered graphs that represent two
different aspects of structural similarity.
3.1 Molecular Similarity Graph
A set of compounds with pairwise similarities can
be represented by a graph: Molecules are associated
with nodes and two nodes are connected by an edge
if their similarity exceeds a certain threshold. This
approach is applied in, e.g., (Wawer et al., 2008;
Lounkine et al., 2010). We additionally annotate
edges with the corresponding similarity values. For
a given set of molecules M we define a similarity
graph G(M) = (V,E) with edge weights w according
to V = M, E = {(u, v) ∈ V × V | sim(u,v) ≥ t}, and
w((u,v)) = sim(u,v) for all (u,v) ∈ E, where sim(·,·)
is a similarity measure defined on molecules and t is
a threshold value with direct influence on the density
of the graph.
While computing adequate structural similarity
measures for molecules is a wide and challenging re-
search topic on its own (Maggiora and Shanmuga-
sundaram, 2011), we rely on standard techniques of-
ten used in practice: Molecules are represented by
so-called fingerprints, i.e., binary vectors of constant
size, where bits encode the presence or absence of cer-
tain fragments (Brown, 2009). We employ the path-
based hash-key fingerprint provided by the chemin-
formatics toolkit CDK (Steinbeck et al., 2006). The
fingerprints are then compared with each other by
computing the Tanimoto coefficient in order to obtain
pairwise similarities.
3.2 Scaffold-based Cluster Hierarchy
A different approach to organizing chemical com-
pound sets is based on a hierarchical classification
scheme representing molecules by their core struc-
tures referred to as scaffolds. The scaffold tree al-
gorithm (Schuffenhauer et al., 2007) builds a tree-like
hierarchy of scaffolds. It essentially proceeds as fol-
lows: For each molecule in the dataset its scaffold
is created by pruning all terminal side chains. Then
the scaffold is successively simplified by removing a
single ring in each step such that the resulting parent
scaffold stays connected. The procedure stops when a
one-ring scaffold is obtained. Since in each step mul-
tiple rings can be removed, a unique parent scaffold
is selected by a set of rules incorporating chemical
knowledge with the aim to preserve the most charac-
teristic ring structure. When the procedure is applied
to a set of molecules, typically some have the same
scaffold and several scaffolds share the same parent
scaffold. A scaffold tree is obtained by merging these
multiple scaffolds and connecting all one-ring scaf-
folds to a virtual root. Figure 1 shows four scaffolds
and their relation in a scaffold tree branch.
Figure 1: A branch of a scaffold tree.
Generating the scaffold tree for a set of molecules
M and connecting all molecules to their scaffold
yields a valid cluster tree for the similarity graph
G(M). While the scaffold tree concept has been suc-
cessfully applied to various research tasks (Wetzel
et al., 2009; Bon and Waldmann, 2010), an obvi-
ous conceptual weakness is that side chains are not
taken into account although they may constitute key
functional groups (Irwin, 2009). Therefore, the com-
bination with a similarity graph based on a whole-
molecule structural similarity measure may help to al-
leviate this drawback.
4 EDGE-AWARE DRAWING
OF CLUSTERED GRAPHS
Visualizing the hierarchy provided by the scaffold tree
and drawing edges of the similarity graph at the same
time turned out to be a challenge. The main prob-
lem is that the hierarchy is not related to the similar-
ity graph, because nodes contained in a cluster are not
necessarily similar. When the original method pro-
posed in (Gronemann and J
¨
unger, 2012) is applied to
these graphs, the results are rather unpleasant. Es-
pecially on very sparse graphs, edge clutter occurs.
In (Gronemann and J
¨
unger, 2012), where a clustering
MolMap-VisualizingMoleculeLibrariesasTopographicMaps
517

a
b
h
d
e
f
g
c
(a) Clustered Graph
a b c d e
f g
h
(b) Input Cluster Tree
a b c d e
f g
h
(c) Extended Cluster Tree
Figure 2: Example of a clustered graph (a) with cluster tree (b). The extended cluster tree (c) contains dummy nodes deter-
mined by betweenness based clustering. Dashed shapes in (a) depict the clusters representing these dummy nodes.
method is applied to the input, and thus the clusters
are consistent with the placement algorithm, nodes
that are well connected are placed close to each other,
while nodes with higher graph theoretic distance are
located in different subtrees. Before we present two
improvements, we sketch the outline of the original
method. First, the input graph is clustered using the
algorithm of (Girvan and Newman, 2002) to obtain
a cluster hierarchy with the aforementioned proper-
ties. Then a tree mapping approach called fat polygon
partitioning, based on (de Berg et al., 2010), is used.
The nodes are placed inside their partition that form a
nested structure of convex polygons representing the
hierarchy. The layout is then transformed into a trian-
gle mesh by applying a Delaunay triangulation. This
mesh serves both as a basis for drawing a topographic
map and as a routing network for edge bundling. For
more details, see (Gronemann and J
¨
unger, 2012).
In the following we present two improvements
of the original method. First, we suggest to extend
the input hierarchy by adding virtual clusters with-
out changing the nested structure of the input. These
new clusters help to place highly connected groups of
nodes together. Second, the fat polygon partitioning is
modified to optimize edge length and to place clusters
based on an arbitrary edge set, while still generating
good polygons. The goal is to make the tree map al-
gorithm aware of the edges and exploit the degrees of
freedom offered by the input hierarchy and the poly-
gon partitioning. Finally, we evaluate the modifica-
tions based on the instances of our application area.
4.1 Extending the Input Hierarchy
The inner nodes of the scaffold tree usually contain
many children. In this case the fat polygon partition
must create a binary subtree for the subdivision pro-
cedure. However, since the provided input hierarchy
is not edge-aware, the subdivision procedure may re-
sult in edge clutter. This is due to the fact that highly
connected child clusters are placed in distant subtrees.
In order to solve this problem, we use edge between-
ness clustering to extend the input hierarchy. The al-
gorithm proposed in (Girvan and Newman, 2002) is
rather simple. For all edges, the betweenness score
is calculated and the edges with the highest score are
removed. This procedure is repeated until the graph
becomes disconnected. The connected components
serve as clusters on which the method recurses.
This method can easily be adapted to work on an
existing hierarchy. We traverse the input hierarchy
top-down. For each cluster C with children C
1
,...,C
n
,
n > 2, we construct a graph G(C) induced by the
underlying edge set E and the children of C. Let
V (C
i
) denote the graph nodes contained in the subtree
rooted at C
i
. Let E(C
i
,C
j
) = E ∩(V (C
i
) ×V (C
j
)) de-
note the edges having one end point in C
i
and the other
in C
j
. The obvious way to obtain the inter-cluster
edge weights w(C
i
,C
j
) is to sum up the ‘cluster-
parallel’ edge weights according to
w(C
i
,C
j
) =
∑
e∈E(C
i
,C
j
)
w(e).
The original algorithm is then used to obtain a hierar-
chy for this graph, which we can insert into the exist-
ing subtree. The leaves of the obtained hierarchy cor-
respond to the children of the cluster node C, which
can be replaced by the root of the hierarchy.
In Figure 2 a small example is displayed. The
dashed shapes are the newly inserted clusters after the
algorithm has decomposed as much as possible with-
out violating the nested structure of the input hierar-
chy. The newly created clusters are used as “ghost
clusters”, which are not visible on the final map. Their
only purpose is to group tightly connected compo-
nents together. In case that the result is not a bi-
nary tree, the transformation used in (Gronemann and
J
¨
unger, 2012) is applied. Notice that the extended hi-
erarchy is based on intra-cluster adjacency only and
does not take external edges into account. This issue
is addressed in the following section.
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
518
v
1
v
2
v
5
v
4
v
3
(a) (b)
v
1
v
2
(c)
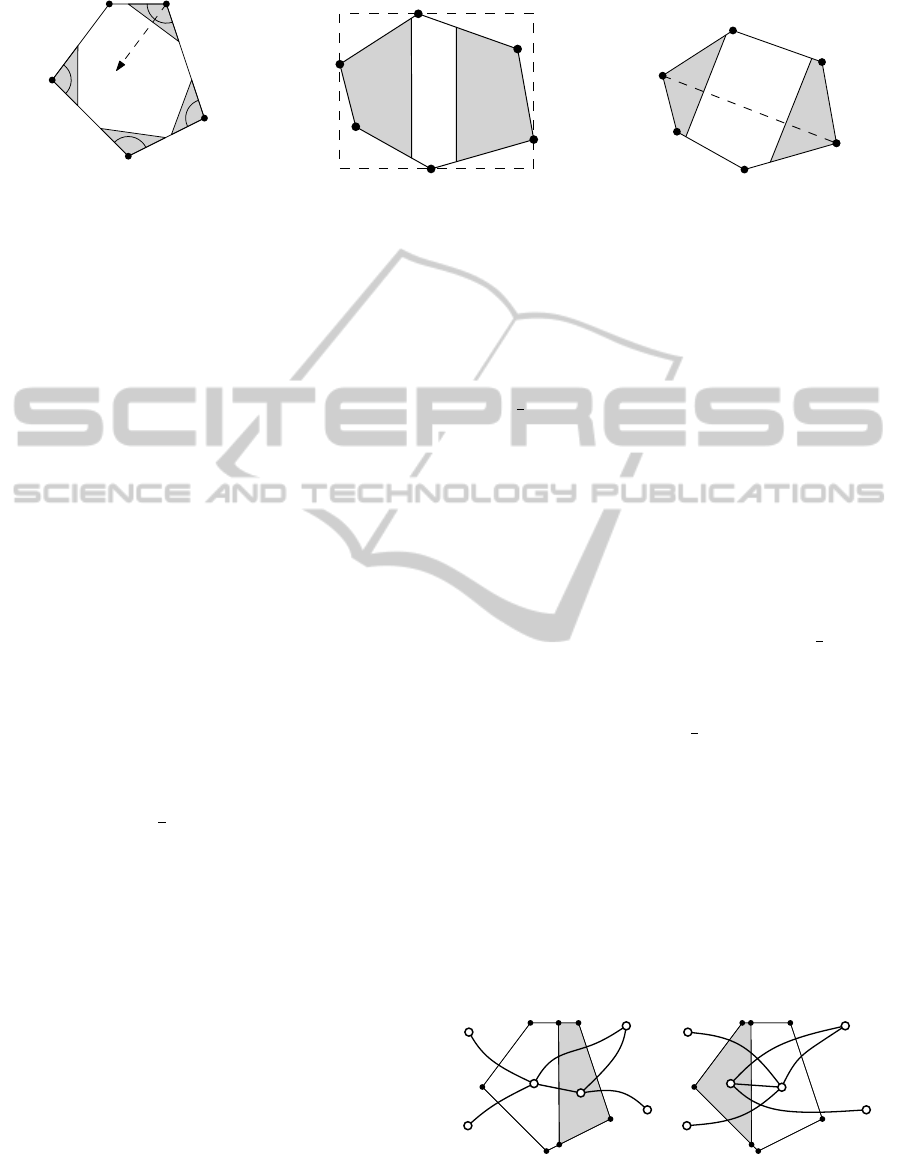
Figure 3: Enumeration of allowed cuts. In (a) we only want to cut off a small part of the polygon. The two choices when
choosing an axis-aligned cut and a cut perpendicular to the diameter defined by v
1
,v
2
are shown in (b) and (c), respectively.
4.2 Edge-aware Polygon Partitioning
In this section we investigate the degrees of freedom
of the polygon partitioning and how to exploit them
to minimize the length of edges between clusters.
A tree map based on fat polygon partitioning fol-
lows the same principle as most tree map algorithms.
The idea is to recursively subdivide a convex polygon
in order to obtain a nested structure of polygons repre-
senting the cluster tree. Starting with the root which
represents the boundary polygon the algorithm pro-
ceeds in a top-down manner: At each cluster node,
the associated polygon is split into two convex sub-
polygons which represent the subtrees rooted at the
two children. The cutting line is chosen, such that the
area of the subpolygons is proportional to the number
of leaves in the corresponding subtrees. We place the
graph nodes, i.e., the leaves of the tree, in the centroid
of the associated polygon computed by the partition-
ing.
The basic problem in the individual steps of the
partitioning algorithm can be summarized as follows:
We are given a convex polygon P with k vertices and
a parameter 0 < a ≤
1
2
, where a is the fraction of the
area we require for the smaller child. Let area(P) de-
note the area of P and diam(P) its diameter, i.e., the
maximum distance between two vertices of P. We
want to find a direction for a cutting line that par-
titions P into two subpolygons P
1
and P
2
, such that
area(P
1
) = a ·area(P) and area(P
2
) = (1 −a)·area(P).
When given a cut direction, we choose the orienta-
tion of the cutting line perpendicular to this direc-
tion. In general finding such a cut is easy for a con-
vex polygon. However, an advantageous character-
istic of the greedy algorithm proposed in (de Berg
et al., 2010) is that it yields polygons with bounded
aspect ratios, where the aspect ratio is defined as
asp(P) = diam(P)
2
/area(P). We want to preserve this
property without unnecessarily restricting the number
of allowed cuts.
In (de Berg et al., 2010) two main cases are dis-
tinguished: In the first case, when we want to cut
off a small piece, that is when a ≤ 1/k
2
, the bisector
at the vertex with the smallest interior angle is taken
as the cut direction. However, the guarantee of the
small aspect ratio only relies on the fact that the small-
est interior angle of a convex polygon is bounded by
π·(1−
2
k
) (de Berg et al., 2010). Thus, we are allowed
to choose any other bisector as long as the interior an-
gle at the corresponding vertex is small enough. In
Figure 3(a) an example is given, where we are allowed
to choose every bisector, except the one at v
2
, which
is not small enough.
In the second case, when a > 1/k
2
, the aspect ratio
of the boundary polygon must be considered. When
P has a good aspect ratio, i.e., asp(P) ≤ k
6
, we are
allowed to choose any direction for a cut (de Berg
et al., 2010). In this case and when a >
1
3
holds,
our implementation chooses an axis-aligned cut nor-
mal to the longest side of the bounding rectangle for
aesthetic reasons, see Figure 3(b). Otherwise, when
asp(P) > k
6
or 1/k
2
< a ≤
1
3
holds, we choose the
direction of the line representing the diameter of the
polygon. This is the line that connects any two ver-
tices of P with maximum distance to each other, cf.
Figure 3(c).
The key idea is to enumerate all allowed cuts for
a given polygon and a parameter a in each step of the
partitioning procedure and to take the one that min-
imizes the edge length. That is, we try to place the
polygon of a child cluster in the direction of clusters
to which it is highly connected. Figure 4 illustrates
(a) (b)
Figure 4: Example for two possible partitions of a polygon
with adjacencies to external clusters. In (a) the total edge
length is less compared to the partition in (b).
MolMap-VisualizingMoleculeLibrariesasTopographicMaps
519
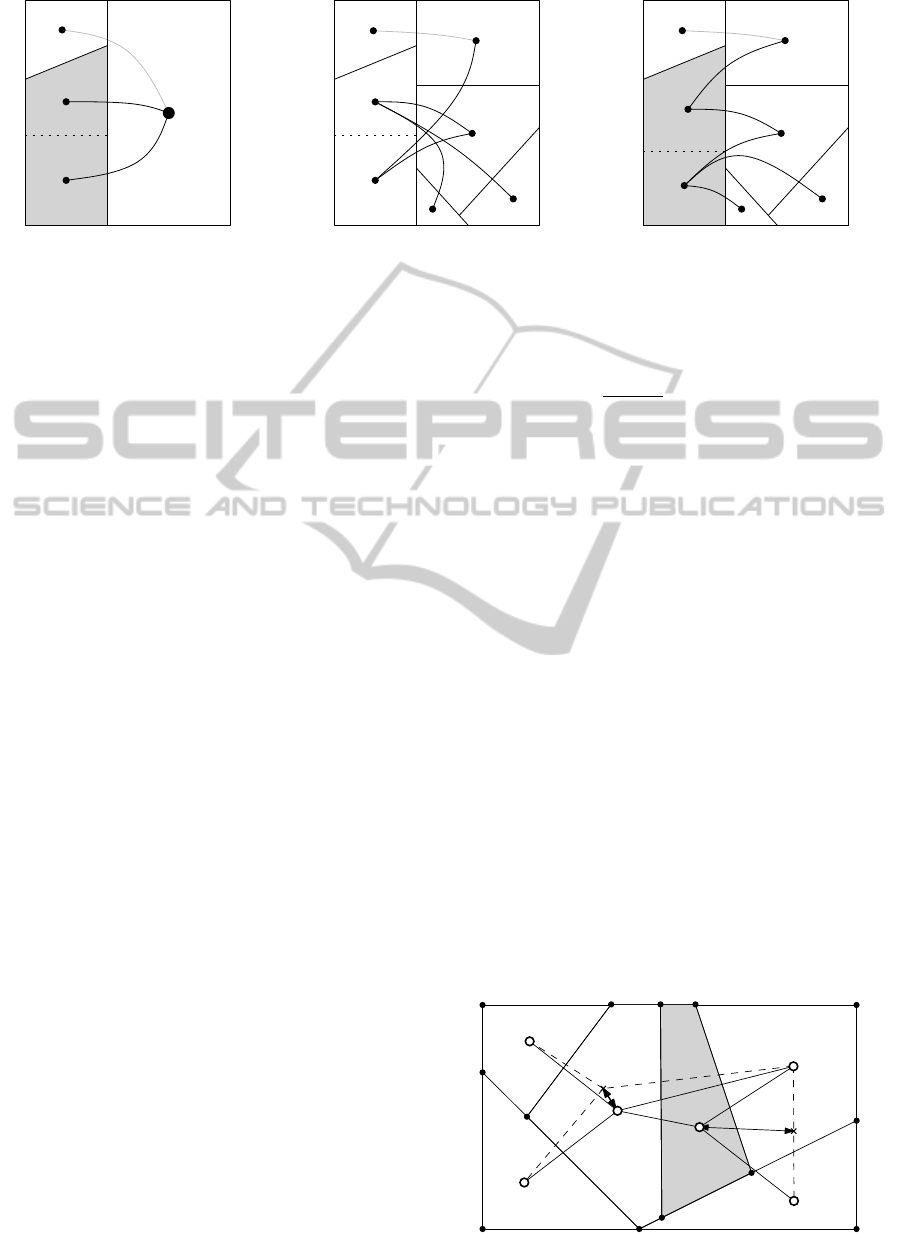
2
3
d, e,
a
b
c
f, g
(a) Initial situation
c
d
f
e
g
a
b
(b) Unbalanced refinement
b
a
c
d
f
e
g
(c) Balanced refinement
Figure 5: Example of layouts obtained for different refinement strategies.
the idea. We will apply this procedure in a top down
manner to obtain a partitioning that is optimized for
edge length. However, there is no accurate informa-
tion available as to where these adjacent clusters are
located because the corresponding polygon has not
been computed yet. Therefore, we propose a heuristic
to decide which cut to use based on the partial knowl-
edge of the surrounding clusters.
The available information on node positions de-
pends on the current state of the subdivision pro-
cess. While the cluster tree is typically traversed in a
depth-first fashion, we propose a different procedure
to achieve a more balanced level of refinement: The
subdivision process always splits the polygon cover-
ing the larger area first. We keep all cluster nodes
whose polygons still have to be partitioned in a pri-
ority queue Q ordered by area requirement. These
nodes, together with the leaves that have been pro-
cessed, form a layer L of nodes with associated poly-
gons that we call active. The polygons of all active
nodes cover the entire boundary polygon and realize
the preliminary layout on which the selection of an
allowed cut is based.
Figure 5 exemplifies the influence of the refine-
ment order. When partitioning the gray polygon con-
taining a and b in Figure 5(a) there is no accurate
information available on the positions of d,e, f ,g.
Therefore, the polygon of a is placed in the middle
since minimizing the distance representing the length
of three inter-cluster edges is prioritized. The result
of this bad decision is displayed in Figure 5(b). When
polygons are partitioned in order of decreasing size
the information on neighboring polygons is more ac-
curate. This typically results in a better final layout.
Figure 5(c) shows the cut that would be chosen after
the large right polygon has been refined.
We introduce additional notation to precisely de-
fine the criterion we use to assess the potential of a
cut to minimize edge lengths. Let C be a node of the
cluster tree. We use ctr(C) to refer to the centroid of
the associated polygon; awc(C) denotes the average
weighted center of the centroids of active polygons
adjacent to C weighted by inter-cluster edges, i.e.,
awc(C) =
1
w(C,L)
∑
P∈L
ctr(P) · w(C, P),
where w(C,L) =
∑
P∈L
w(C,P). The value of awc(C)
can be considered as the preferred location of (the
centroid of) the polygon associated with C.
Consider an active node C ∈ Q with children C
1
and C
2
. Each allowed cut assigns a subpolygon to the
two children, cf. Figure 3. The idea is to choose the
cut that minimizes the distance between the centroids
of the subpolygons and their preferred positions ac-
cording to the average weighted center. We define
the distance between the two points associated with a
node C as
dist(C) =
k
awc(C) −ctr(C)
k
if w(C,L) 6= 0,
0 otherwise.
Note that in the second case there are no edges leav-
ing the cluster C and the position of the polygon has
no effect on edge lengths. We choose the cut that min-
imizes
∑
i∈{1,2}
dist(C
i
) · w(C
i
,L), (1)
where the factor w(C
i
,L) reflects the impact of the in-
dividual children. Figure 6 illustrates the method for
a given cut.
awc(A)
awc(B)
ctr(B)
ctr(A)
Figure 6: Edge-aware cut selection
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
520

0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
1.0 1.5 2.0 4.0 8.0
Average Weighted Edge Length
Density
Input Hierarchy
Edge-aware FPP + Input Hierarchy
Extended Hierarchy
Edge-aware FPP + Extended Hierarchy
Figure 7: Comparison of the average weighted edge length.
Putting all the above steps together, we can outline
the algorithm: We start with the root of the tree, assign
it the boundary polygon given as input and add it to
Q. Then we repeat the following steps until all leaves
have been processed.
1. Pop a node C with its boundary polygon P from
the queue Q.
2. If C is a leaf, add it to the active nodes and go to
the first step, otherwise C must be partitioned.
3. Compute the fraction a of the area required for the
smaller child of C and check which case applies
based on a and P.
4. Enumerate all allowed cuts and choose the cut that
minimizes Equation (1).
5. Enqueue the two children in Q.
Notice that neither C nor its children are active during
the cut enumeration phase.
5 RESULTS & APPLICATION
In this section, we report on an experimental evalu-
ation of the proposed techniques to minimize edge
length and introduce several domain-specific exten-
sions.
5.1 Evaluation of Edge Length
In order to determine the effect on the layout, we
tested our approach on real-world datasets. The
instances were derived from a publicly available
pyruvate kinase high-throughput screening dataset
3
,
which has previously been used in (Wetzel et al.,
3
Available from PubChem BioAssay, AID 361
2009) and consists of 51, 415 compounds. We gener-
ated 20 subsets by randomly selecting 200, 400, 600
and 800 compounds, respectively. For each subset
we created clustered graphs according to the graph
model described in Section 3 with varying densities
by selecting suitable threshold parameters. We report
the average weighted edge length of these instances
drawn in the unit square. Figure 7 displays the re-
sults for different densities. It is clearly visible that
the two presented approaches affect the edge length
in a positive way. As expected, the effect is less when
the density increases. Interestingly, the changes made
to the fat polygon partitioning are significant even for
higher densities, unlike the extension of the cluster
hierarchy. The latter performs well on the sparse in-
stances, while the result is slightly worse for the high-
est density in comparison to the edge-aware fat poly-
gon partitioning. The runtime
4
for the largest instance
with |V | = 800 and |E| = 6400 is about 7s for the clus-
ter extension and 0.6s for the edge-aware fat polygon
partitioning.
Figure 8 shows an example which illustrates the
effectiveness of the proposed techniques. Note that
in Figure 8(a) there are several long edges, some of
which even cross the entire drawing area connecting
nodes in the bottom left corner (cluster A) to nodes
in the top right corner (cluster E). In such cases edges
are bundled to avoid visual clutter. However, a down-
side of edge bundling is that individual edges become
difficult to identify. In Figure 8(b) the same instance
is drawn using the proposed optimization techniques.
Here, the layout leads to short edges and individ-
ual connections are easily recognizable. Since highly
similar molecules are placed close to each other, this
drawing is also clearly preferable from the application
point of view.
4
Machine with Core i7 2.7 GHz and 8 GB RAM
MolMap-VisualizingMoleculeLibrariesasTopographicMaps
521

(a) Without improvements
(b) Extended hierarchy and edge-aware partitioning
Figure 8: Visual comparison of the layout generated by the
original approach (a) and the proposed method (b). Letters
indicate corresponding main clusters.
5.2 Representation of Chemical
Information
In this section we report on the application of our ap-
proach to a real-world dataset and describe several
extensions we incorporated to meet requirements of
the application area. To focus on relevant molecules
we filtered the dataset used in Section 5.1 for active
compounds with AC
50
≤ 10µM and decreasing activ-
ity direction, which yields a dataset with 432 com-
pounds. From this subset we selected all molecules
associated with scaffold tree branches containing at
least 10 compounds. The threshold for the similarity
graph was set to t = 0.5. While our approach also
works smoothly with larger datasets, we decided to
use this small focused dataset consisting of 256 com-
pounds to provide screen shots.
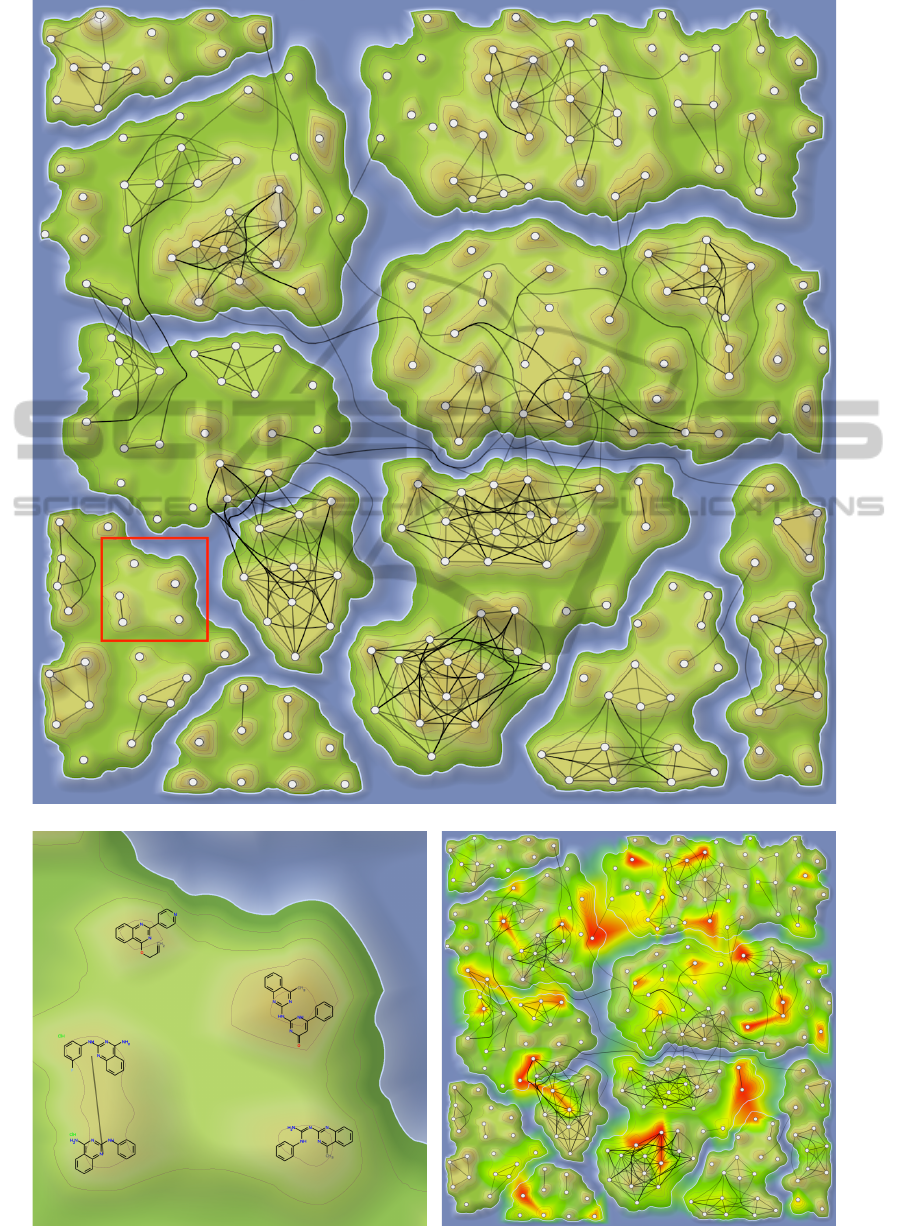
The resulting topographic map is shown in Fig-
ure 9(a). Since the water level is chosen such that each
scaffold tree branch is represented by one island, this
overview directly conveys to what extent branches are
populated by compounds. With our approach the alti-
tude represents the number of rings compounds have
and whenever two molecules are located on the same
hill, they share a common scaffold (according to the
scaffold tree) whose number of rings is represented
by the elevation level of the hill. While edges often
connect molecules on the same islands, there are also
edges connecting molecules placed on different is-
lands (see, e.g., the central island on the left hand side
and the small island south-east) indicating the pres-
ence of highly similar molecules in different branches
of the scaffold tree. Placing these molecules near each
other helps to generate continuous regions of highly
similar molecules and is achieved by our heuristic ap-
proach. Furthermore, we support additional annota-
tions to specifically foster the application in drug dis-
covery.
5.2.1 Depiction of Structural Formulae
The most widely used representation of chemical
compounds are 2D depictions of their structure. To
allow a detailed investigation of structural relation-
ships, we support displaying structural formulae. Fig-
ure 9(b) shows a close-up view of a region of an is-
land. The shown molecules are placed on the same el-
evated plateau indicating their common two-ring scaf-
fold. The two molecules on the left hand side even
share a scaffold with three rings.
5.2.2 Mapping of Properties
While the topographic map is generated taking only
structural similarity of molecules into account, relat-
ing structural features with certain properties is of ut-
most importance in drug discovery. We support the
visualization of molecular properties by superimpos-
ing a heat map, faintly reminiscent of a temperature
related weather map. Figure 9(c) shows an example
where regions of highly active molecules are high-
lighted in red. The color gradient from red to green
represents decreasing activity. Regions not colored
are populated by less active molecules. The heat map
is generated by computing a Delaunay triangulation
and, similar to the topographic map, visualized using
color encoded levels based on the property values.
6 CONCLUSIONS & OUTLOOK
Organizing compound libraries by structural similar-
ity in a way that allows for intuitive navigation for
chemical tasks is challenging. We proposed a clus-
tered graph model and adapted a technique to draw
them as topographic maps. We have already received
some first positive feedback from domain experts, and
the representation as topographic map has been well
accepted. However, a large-scale systematic evalua-
tion of the method based on a wide range of datasets
and different chemical workflows is out of the scope
of this article, but an important future task.
The goal to place similar molecules near each
other while respecting the cluster hierarchy leads to
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
522
(a) Real-world instance
(b) Close-up view (c) Superimposed heat map
Figure 9: Visualization of the real-world instance consisting of 256 molecules (a) and the same map with property annotations
(c). In (b) a close-up view of the region highlighted in red shows five molecules represented by structural formulae.
MolMap-VisualizingMoleculeLibrariesasTopographicMaps
523

the graph drawing problem to minimize edge length in
the known approach (Gronemann and J
¨
unger, 2012).
To achieve this goal we proposed a heuristic that ex-
ploits the degrees of freedom in the polygon partition-
ing procedure in order to avoid long edges. The effec-
tiveness of the method has been demonstrated by an
experimental evaluation using real-world instances.
ACKNOWLEDGEMENTS
We would like to thank Claude Ostermann and
Philipp Thiel for their valuable feedback and for shar-
ing their chemical knowledge. Research was sup-
ported by the German Research Foundation (DFG),
priority programme “Algorithm Engineering” (SPP
1307).
REFERENCES
Bon, R. S. and Waldmann, H. (2010). Bioactivity-guided
navigation of chemical space. Acc. Chem. Res.,
43(8):1103–1114.
Brown, N. (2009). Chemoinformatics - an introduction for
computer scientists. ACM Comput. Surv., 41(2).
de Berg, M., Onak, K., and Sidiropoulos, A. (2010). Fat
polygonal partitions with applications to visualization
and embeddings. CoRR, abs/1009.1866.
Fabrikant, S. I., Montello, D. R., and Mark, D. M. (2010).
The natural landscape metaphor in information visu-
alization: The role of commonsense geomorphology.
J. Am. Soc. Inf. Sci. Technol., 61(2):253–270.
Fruchterman, T. M. J. and Reingold, E. M. (1991). Graph
drawing by force-directed placement. Softw., Pract.
Exper., 21(11):1129–1164.
Gansner, E. R., Hu, Y., and Kobourov, S. G. (2010). GMap:
Visualizing graphs and clusters as maps. In Pacific
Visualization Symposium (PacificVis), pages 201–208.
IEEE.
Gansner, E. R., Hu, Y., Kobourov, S. G., and Volinsky, C.
(2009). Putting recommendations on the map: visual-
izing clusters and relations. In Proc. ACM Conference
on Recommender Systems, pages 345–348.
Girvan, M. and Newman, M. E. J. (2002). Community
structure in social and biological networks. Proc. of
the National Academy of Sciences, 99:7821–7826.
Gronemann, M. and J
¨
unger, M. (2012). Drawing clustered
graphs as topographic maps. In 20th International
Symposium on Graph Drawing.
Herhaus, C., Karch, O., Bremm, S., and Rippmann,
F. (2009). MolWind - mapping molecule spaces
to geospatial worlds. Chemistry Central Journal,
3(Suppl 1):P32.
Huang, M. and Eades, P. (1998). A fully animated interac-
tive system for clustering and navigating huge graphs.
In Graph Drawing, volume 1547 of Lecture Notes in
Computer Science, pages 374–383. Springer.
Irwin, J. J. (2009). Staring off into chemical space. Nat.
Chem. Biol., 5(8):536–537.
Johnson, B. and Shneiderman, B. (1991). Tree-maps: a
space-filling approach to the visualization of hierar-
chical information structures. In Proc. of the 2nd Con-
ference on Visualization, pages 284–291.
Klein, K., Kriege, N., and Mutzel, P. (2012). Scaf-
fold Hunter – visual analysis of chemical compound
databases. In Proc. Int. Conf. on Computer Graphics
Theory and Applications and Int. Conf. on Informa-
tion Visualization Theory and Applications (GRAPP
& IVAPP), pages 626–635.
Lounkine, E., Wawer, M., Wassermann, A. M., and Bajo-
rath, J. (2010). SARANEA: a freely available program
to mine structure-activity and structure-selectivity re-
lationship information in compound data sets. J.
Chem. Inf. Model., 50(1):68–78.
Maggiora, G. M. and Shanmugasundaram, V. (2011).
Molecular similarity measures. Methods in Molecu-
lar Biology, 672:39–100.
Schuffenhauer, A., Ertl, P., Roggo, S., Wetzel, S., Koch,
M. A., and Waldmann, H. (2007). The scaffold tree
- visualization of the scaffold universe by hierarchical
scaffold classification. J. Chem. Inf. Model., 47(1):47–
58.
Schuffenhauer, A. and Varin, T. (2011). Rule-based classi-
fication of chemical structures by scaffold. Molecular
Informatics, 30(8):646–664.
Schulz, H.-J. (2011). Treevis.net: A tree visualization ref-
erence. IEEE Computer Graphics and Applications,
31(6):11–15.
Steinbeck, C., Hoppe, C., Kuhn, S., Floris, M., Guha, R.,
and Willighagen, E. L. (2006). Recent developments
of the chemistry development kit (CDK) - an open-
source java library for chemo- and bioinformatics.
Current pharmaceutical design, 12(17):2111–2120.
Strobelt, H., Bertini, E., Braun, J., Deussen, O., Groth, U.,
Mayer, T. U., and Merhof, D. (2012). HiTSEE KN-
IME: a visualization tool for hit selection and analysis
in high-throughput screening experiments for the KN-
IME platform. BMC Bioinformatics, 13 Suppl 8:S4.
Sugiyama, K. and Misue, K. (1991). Visualization of struc-
tural information: Automatic drawing of compound
digraphs. IEEE Trans. SMC, 21(4):876–892.
Wawer, M., Peltason, L., Weskamp, N., Teckentrup, A.,
and Bajorath, J. (2008). Structure-activity relationship
anatomy by network-like similarity graphs and local
structure-activity relationship indices. J. Med. Chem.,
51(19):6075–6084.
Wetzel, S., Klein, K., Renner, S., Rauh, D., Oprea, T. I.,
Mutzel, P., and Waldmann, H. (2009). Interactive ex-
ploration of chemical space with Scaffold Hunter. Na-
ture Chemical Biology, 5(8):581–583.
IVAPP2013-InternationalConferenceonInformationVisualizationTheoryandApplications
524
