The Path Kernel
Andrea Baisero, Florian T. Pokorny, Danica Kragic and Carl Henrik Ek
KTH Royal Institute of Technology, Stockholm, Sweden
Keywords:
Kernel Methods, Sequential Modelling.
Abstract:
Kernel methods have been used very successfully to classify data in various application domains. Traditionally,
kernels have been constructed mainly for vectorial data defined on a specific vector space. Much less work has
been addressing the development of kernel functions for non-vectorial data. In this paper, we present a new
kernel for encoding sequential data. We present our results comparing the proposed kernel to the state of the
art, showing a significant improvement in classification and a much improved robustness and interpretability.
1 INTRODUCTION
Machine Learning methods have had an enormous
impact on a large range of fields such as Computer
Vision, Robotics and Computational Biology. These
methods have allowed researchers to exploit evidence
from data to learn models in a principled manner. One
of the most important developments has been that
of Kernel Methods (Cristianini and Shawe-Taylor,
2006), which embed the input data in a potentially
high-dimensional vector space with the intention of
achieving improved robustness of classification and
regression techniques. The main benefit of Kernel
Methods is that, rather than defining an explicit fea-
ture space that has the desired properties, the em-
bedding is characterised implicitly through the choice
of a kernel function which models the inner prod-
uct in an induced space. This creates a very natural
paradigm for recovering the desired characteristics of
a representation. Kernel functions based on a station-
ary distances (usually an L
p
−norm) have been partic-
ularly successful in this context (Buhmann and Mar-
tin, 2003). However, for many application domains,
the data does not naturally lend itself to a finite dimen-
sional vectorial representation. Symbolic sequences
and graphs, for example, pose a problem for such ker-
nels.
For non-vectorial data, the techniques used for
learning and inference are generally much less de-
veloped. A desirable approach is hence to first place
the data in a vector space where the whole range of
powerful machine learning algorithms can be applied.
Simple approaches such as the Bag-of-Words model,
which creates a vectorial representation based on oc-
currence counts of specific representative “words”,
have had a big impact on Computer Vision (Sivic
and Zisserman, 2009). These methods incorporate
the fact that a distance in the observed space of im-
age features does not necessarily reflect a similarity.
Another approach where strings are transformed into
a vectorial representation before a kernel method is
applied has been the development of string kernels
(Lodhi et al., 2002; Saunders et al., 2002). Such ker-
nels open up a whole range of powerful techniques for
non-vectorial data and have been been applied suc-
cessfully to Robotics (Luo et al., 2011), Computer
Vision (Li and Zhu, 2006) and Biology (Leslie and
Kuang, 2004). Other related works are based on con-
volution kernels (Haussler, 1999), which recover a
vectorial representation that respects the structure of
a graph. Another approach to define an inner prod-
uct between sequences is to search for a space where
similarity is reflected by “how well” sequences align
(Watkins, 1999; Cuturi et al., 2007; Cuturi, 2010).
In this paper, we present a new kernel for repre-
senting sequences of symbols which extends and fur-
ther develops the concept of sequence alignment. Our
kernel is based on a ground space which encodes sim-
ilarities between the symbols in a sequence. We show
that our kernel is a significant improvement compared
the state of the art both in terms of computational
complexity and in terms of its ability to represent the
data.
The paper is organised as follows: In §2, we out-
line the problem scenario and provide a structure for
the remaining discussion. §3 introduces our approach
and §4 provides the experimental results. Finally, we
conclude with §5.
50
Baisero A., T. Pokorny F., Kragic D. and Henrik Ek C. (2013).
The Path Kernel.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 50-57
DOI: 10.5220/0004267300500057
Copyright
c
 SciTePress

2 KERNELS AND SEQUENCES
Before we proceed with describing previous work for
creating kernel induced feature spaces for sequences,
we will clarify our notation and our notion of ker-
nels. When discussing kernels in the context of ma-
chine learning, we have to distinguish between sev-
eral uses of the word kernel. In this paper, a ker-
nel denotes any symmetric function k : X × X → R,
where X is a non-empty set (Haasdonk and Burkhardt,
2007). A positive semi-definite (psd) kernel is a ker-
nel k : X × X → R such that
∑
n
i, j
c
i
c
j
k(x
i
,x
j
) > 0 for
any {x
1
,...,x
n
} ⊂ X, n ∈ N and c
1
,...c
n
∈ R. If the
previous inequality is strict when c
i
6= 0 for at least
one i ∈ {1, . . . , n}, the kernel is called positive definite
(pd). Further specialisations, such as negative definite
(nd) kernels, exist and are of independent interest.
While strong theoretical results on the existence
of embeddings corresponding to psd kernels exist
(Berlinet and Thomas-Agnan, 2004, p.22), non-psd
kernel functions can still be useful in applications.
Examples of kernels that are known to be neither pd
nor psd, but which are still successfully used in clas-
sification include (Haasdonk, 2005). On another note,
there are also kernels which are conjectured to be psd,
and which have been shown to be psd in experiments,
but for which there currently is no proof for the cor-
responding positivity (Bahlmann et al., 2002).
In this work, we consider finite sequences of
symbols belonging to an alphabet set Σ, i.e. s =
(s
1
,s
2
,...,s
|s|
) denotes such a sequence, with s
i
∈ Σ,
and where |s| ∈ N
0
denotes the length of the sequence.
We denote a subsequence (s
a
,...,s
b
), for 1 6 a < b 6
|s|, by s
a:b
. When the indices a or b are omitted, they
implicitly refer to 1 or |s| respectively. The inverse of
a sequence s is defined by inv (s)
i
= s
|s|−(i−1)
.
In this work, we assume that we are given a psd
kernel function k
Σ
: Σ × Σ → R describing the similar-
ity between elements of the alphabet Σ and will refer
to k
Σ
as the ground kernel.
Given k
Σ
, we can now define the path matrix.
Definition 1 (Path Matrix). Given two finite se-
quences s,t with elements in an alphabet set Σ and
a kernel k
Σ
: Σ × Σ → R, we define the path matrix
G(s,t) ∈ R
|s|×|t|
by [G(s,t)]
i j
= k
Σ
(s
i
,t
j
).
We denote δ
00
def
= (0, 0), δ
10
def
= (1, 0), δ
01
def
= (0, 1),
δ
11
def
= (1,1) and S
def
= {δ
10
,δ
01
,δ
11
}. S is called the set
of admissible steps. A sequence of admissible steps
starting from (1,1) defines the notion of a path:
Definition 2 (Path). A path over a m × n path-matrix
M is a map γ : {1,...,
|
γ
|
} → Z
>0
× Z
>0
such that
γ(1) = (1,1), (1)
γ(i +1) = γ(i) + δ
i
, (2)
for 1 6 i <
|
γ
|
, with δ
i
∈ S,
γ(
|
γ
|
) = (m,n). (3)
|
γ
|
and δ
i
denote the path’s length and i
th
step re-
spectively. Furthermore, we adopt the notation γ(i) =
(γ
X
(i),γ
Y
(i)). A path defines stretches, or align-
ments, on the input sequences according to s
γ
X
=
(s
γ
X
(1)
,...,s
γ
X
(
|
γ
|
)
) and t
γ
Y
= (t
γ
Y
(1)
,...,t
γ
Y
(
|
γ
|
)
).
We denote the set of all paths on a m × n matrix
as Γ(m,n). Its cardinality is equal to the Delannoy
number D(m,n).
2.1 Sequence Similarity Measures
A popular similarity measure between time-series is
Dynamic Time Warping (DTW) (Sakoe and Chiba,
1978; Gudmundsson et al., 2008), which determines
the distance between two sequences s and t as the
minimal score obtained by all paths, i.e.
d
DTW
(s,t) = min
γ∈Γ
D
s,t
(γ), (4)
where D
s,t
represents the score of a path γ defined by
D
s,t
(γ) =
|
γ
|
∑
i=1
ϕ(s
γ
X
(i)
,t
γ
Y
(i)
), (5)
where ϕ is some given similarity measure. However,
DTW lacks a geometrical interpretation in the sense
that it does not necessarily respect the triangle in-
equality (Cuturi et al., 2007). Furthermore, this simi-
larity measure is not likely to be robust as it only uses
information from the minimal cost alignment.
Taking the above into consideration, Cuturi sug-
gests a kernel referred to as the Global Alignment
Kernel (Cuturi et al., 2007). Instead of considering
the minimum over all paths, the Global Alignment
Kernel combines all possible path scores. The kernel
makes use of an exponentiated soft-minimum of all
scores, generating a more robust result which reflects
the contents of all possible paths:
k
GA
(s,t) =
∑
γ∈Γ
e
−D
s,t
(γ)
. (6)
By taking the ground kernel to be k
Σ
(α,β) = e
−ϕ(α,β)
,
k
GA
can be described using the path matrix as
k
GA
(s,t) =
∑
γ∈Γ
|
γ
|
∏
i=1
G(s,t)
γ(i)
. (7)
The leading principle in this approach is hence a com-
bination of kernels on the level of symbols over all
ThePathKernel
51

A
N
N
A
B A N A N A
(a)
B A N A N A
A
N
N
A
0
0
1 1 1
1 1
1 1
1 1 1
0
0
0
0
0
0
0
0
0
0
0
0
(b)
A
N
N
A
B A N A N A
1 1 1
1 1 1
1 1
1 1
(c)
Figure 1: Illustration of the concept of paths and the contents of G(s,t) for s = “ANNA” and t = “BANANA”. On the left,
we illustrate a small number of paths which traverse G. The path kernel makes use of these, together with all the other
paths, to collect data from the matrix and to extract a final score. In the center, we display the contents of G(s,t), assuming
k
Σ
(α,β) = δ
αβ
, i.e. Kroenecker’s delta function. On the right, we highlight the corresponding diagonals whose number,
length and position relate to the similarity between the subsequences of s and t.
paths along G(s,t). Cuturi shows that incorporating
all the elements of G(s,t) into the final results can
vastly improve classification compared to using only
the minimal cost path. Furthermore, k
GA
is proven to
be psd under the condition that both k
Σ
and
k
Σ
1+k
Σ
are
psd (Cuturi et al., 2007), giving foundation to its geo-
metrical interpretation.
However, Cuturi’s kernel makes use of products
between ground kernel evaluations along a path. This
implies that the score for a complete path will be very
small if ϕ(s
i
,t
j
) is sufficiently large, which leads to
the problem of diagonally dominant kernel matrices
(Gudmundsson et al., 2008; Cuturi, 2010) from which
the global alignment kernel suffers. The issue is par-
ticularly troubling when occurring at positions near
the top-left or bottom-right corners of the path ma-
trix because it will affect many of the paths. Fur-
thermore, paths contribute with equal weight to the
value of the kernel. To reduce this effect it is sug-
gested in (Cuturi et al., 2007) to rescale the kernel
values and use its logarithm instead. We argue that
paths which travel closest to the main diagonal of the
path matrix should be considered as more important
than others, as they minimise the distortion imposed
on the input sequences, i.e. s
γ
X
and t
γ
Y
are then most
similar to s and t. To rectify this and to include a pref-
erence towards diagonal paths, a generalisation called
the Triangular Global Alignment Kernel was devel-
oped, which considers only a subset of the paths (Cu-
turi, 2010). This generalisation imposes a crude pref-
erence for paths which do not drift far away from the
main diagonal.
In this paper, we develop a different approach
by introducing a weighting of the paths in Γ based
on the number of diagonal and off-diagonal steps
taken. We manipulate the weights to encode a prefer-
ence towards consecutive diagonal steps while at the
same time accumulating information about all possi-
ble paths. Furthermore, by replacing the accumula-
tion of symbol kernel responses along the path using
a summation rather than a product, the kernel’s eval-
uation reflects more gracefully the structure of the se-
quences and avoids abrupt changes in value.
3 THE PATH KERNEL
In this section, we will describe our proposed kernel
which we will refer to as the path kernel.
Figure 1 illustrates the contents of a path matrix in
a simplified example, showing the emergence of diag-
onal patterns when the two sequences are in good cor-
respondence. Table 1 shows the resulting alignments
associated with the paths shown in Figure 1. We argue
that the values, the length and the location of these di-
agonals positively reflect the relation between the in-
puts and should thus be considered in the formulation
of a good kernel. High values imply a good match on
the ground kernel level, while their length encodes the
extent of the match. On the other hand, the position
relative to the main diagonal reflects how much the
input sequences had to be “stretched” in order for the
match to be encountered. We wish to have a feature
space where a smaller stretch implies a better corre-
spondence between the sequences.
Let us now define a new kernel that incorporates
different weightings depending on the steps used to
travel along a path.
Definition 3 (Path Kernel). For any sequences s,t, we
define
k
PAT H
(s,t)
def
=













k
Σ
(s
1
,t
1
)
+C
HV
k
PAT H
(s
2:
,t)
+C
HV
k
PAT H
(s,t
2:
)
+C
D
k
PAT H
(s
2:
,t
2:
)
|s| > 1|t| > 1,
0 otherwise,
(8)
where C
HV
and C
D
represent weights assigned to
vertical or horizontal steps and diagonal steps re-
spectively. By enforcing the constrains C
HV
> 0 and
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
52

Table 1: Stretches associated to the paths in Figure 1a with
the underlined substrings denoting a repeated symbol. Note
that, even though γ
2
and γ
3
produce the same stretches, they
traverse the matrix differently and should thus be consid-
ered separately.
stretches
γ
1
A N N A A A A A A
γ
2
A N N N N A
B B B B A N A N A B A N A N A
γ
3
A N N N N A
γ
4
A A A A A A N N A
B A N A N A B A N A N A A A A
C
D
> C
HV
, we aim to increase the relative importance
of paths with many diagonal steps.
The symmetry of the kernel is easily verifiable.
On the other hand, positive definiteness remains to
be proven, although all our experimental results have
yielded psd kernel matrices in practice.
3.1 Efficient Computation
Kernel methods often require the computation of a
kernel function on a large dataset, where the num-
ber of kernel evaluations will grow quadratic with
the number of data-points. It is hence essential that
the kernel evaluations themselves are efficiently com-
putable.
Not only can the path kernel be evaluated us-
ing a Dynamic Programming algorithm which avoids
the expensive recursion in (8) and which achieves a
computational complexity comparable with DTW and
k
GA
, but it can also be computed very efficiently using
the following alternative formulation:
k
PATH
(s,t) =
∑
i j
G(s,t)
i j
ω
PATH i j
, (9)
[ω
PATH
]
i j
= (10)
min(i, j)−1
∑
d=0
C
i+ j−2−2d
HV
C
d
D
(d, i − 1 − d, j − 1 − d)!.
The usefulness of (9) comes from the fact that the
contents of the weight matrix ω
PATH
do not really de-
pend on s,t since ω
PATH
can in fact be pre-computed
up to an adequate size
1
(see Figure 2). After this, the
evaluation of the kernel for input of sizes m and n is
achieved by simply selecting the sub-matrix ranging
from (1,1) to (m,n); the remaining matrix multiplica-
tion can then be efficiently carried out. By taking ad-
vantage of this, one can evaluate the kernel at speeds
depending only on the speed of the evaluation of G
and the speed of a simple matrix multiplication (with
the initial overhead consisting of the pre-computation
1
For any specific dataset, that would be the length of the
longest sequence.
Figure 2: On the left, a precomputed 15 × 15 weight
matrix with C
HV
= .3 and C
D
= .34 is used to select a
10 × 12 weight matrix which can then be used to evalu-
ate k
PAT H
(s,t) for input sizes |s| = 10 and |t| = 12. On the
right, the inversion invariant
˜
ω
PAT H
corresponding to
˜
k
PAT H
for the same input sizes is displayed.
of ω
PATH
). The weight matrix can also computed
through an efficient and very simple Dynamic Pro-
gramming algorithm similar to the one which can be
used to evaluate the kernel itself.
We call a kernel satisfying k(s,t) =
k(inv(s),inv (t)) inversion invariant. If a kernel
k does not naturally have this property, it can be
enforced by replacing k with
˜
k(s,t) =
k(s,t) + k(inv (s),inv (t))
2
. (11)
The path kernel is not originally inversion invariant,
but invariance can be enforced without the need for a
double computation of the kernel for each evaluation.
This is done by modifying the selected sub-matrix of
ω
PATH
as follows: for any two inputs with lengths m
and n, we replace the weight matrix ω
PATH
by
[
˜
ω
PATH
]
i j
=
ω
PATH i j
+ ω
PATH m−i+1,n− j+1
2
, (12)
and then proceed using this weight matrix.
3.2 Ground Kernel Choice
The path kernel is based on a ground kernel which,
apart from being a psd function, is not constrained in
any other way. However, we show in this paragraph
that an arbitrarily k
Σ
may lead to undesirable results.
Assume an alphabet and a ground kernel such that
α,β ∈ Σ, k
Σ
(α,α) = k
Σ
(β,β) = 1 and k
Σ
(α,β) = −1.
Given the input sequences s = (α,β,. ..,α,β) and
t = (β, α, . . . , β, α), one may be inclined to say that
s and t are very similar because each can be ob-
tained from the other by cyclically shifting the sym-
bols by one position. However, the contents of G(s,t)
show a collection of ones and negative ones organ-
ised in a chessboard-like disposition. This obviously
leads to heavy fluctuations during the computation of
k
PATH
(s,t) and to potentially very small values. Fur-
thermore, the issue is present even in the computation
ThePathKernel
53

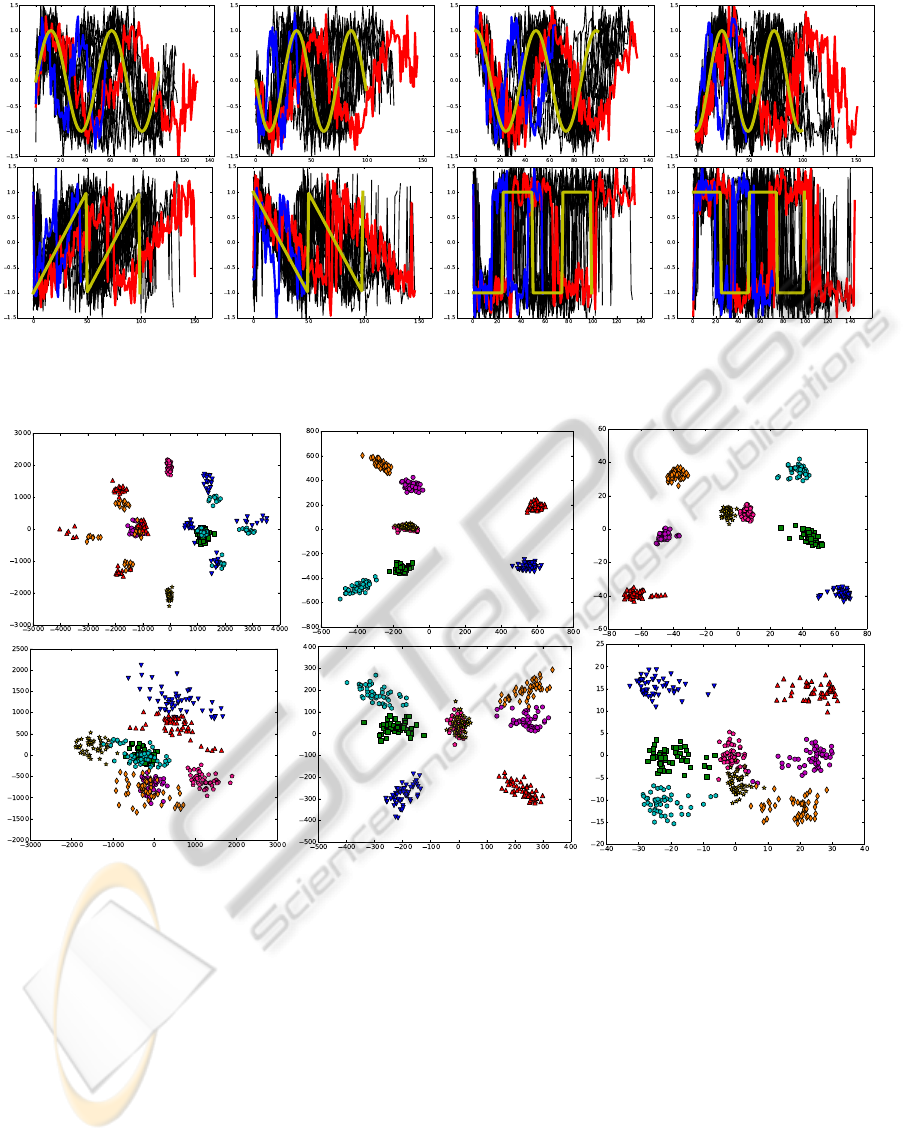
Figure 3: The figure above shows the eight different waveforms used for the classification for a noise level corresponding to
σ
{l,i,o}
= 5. The golden curve depicts the base waveform without noise while the blue and red curves show the shortest and
the longest noisy example respectively. The black curves display the remaining examples in the database.
Figure 4: The above figure displays the two dimensional principal subspace for the Global Alignment Kernel (left), Dynamic
Time Warping (middle) and the Path Kernel (right). The first row has a generating noise with σ
{l,i,o}
= 2, while, in the bottom
row, the noise is increased to σ
{l,i,o}
= 5, corresponding to the waveforms in Figure 3. The different waveforms are displayed
as follows: sine and -sine as a magenta circle and a green square, cosine and -cosine as a pink pentagon and a yellow star,
sawtooth and -sawtooth as a light-blue hexagon and an orange diamond and square and -square as a blue and a red triangle
respectively.
of k
PATH
(s,s) and k
PATH
(t,t) which is not desirable
under any circumstance.
This problem is however easily rectifiable by con-
sidering only ground kernels that yield non-negative
results on elements of Σ.
4 EXPERIMENTS
In this section, we present the results of experiments
performed with the proposed kernel. In particular, we
perform two separate quantitative experiments that, in
addition to our qualitative results, shed some light on
the behaviour of the proposed method in comparison
to previous work. In the first experiment, we generate
eight different classes of uni-variate sequences. Each
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
54

class consists of a periodic waveform namely ±sine,
±cosine, ±sawtooth and ±square. From these, we
generate noisy versions by performing three different
operations:
• The length of the sequence is generated by sam-
pling from a normal distribution N (100, σ
2
l
),
rounding the result and rejecting non-positive
lengths.
• We obtain an input sequence as |s| equidistant
numbers spanning 2 periods of the wave; we then
add to each element an input noise which follows
a normal distribution N (0,σ
2
i
).
• We feed the noisy input sequence to the gener-
ating waveform and get an output sequence, to
which we add output noise which follows a nor-
mal distribution N (0,σ
2
o
),
Figure 3 shows the sequences for the parameter set-
ting σ
{l,i,o}
= 5. This corresponds to the setting which
we will use to present our main results. We will com-
pare our approach to k
GA
as well as the non-psd ker-
nel obtained by using the negative exponential of the
DTW distance,
k
DTW
(s,t) = e
−d
DTW
(s,t)
. (13)
The path kernel has two different sets of parameters:
the ground kernel and the weights associated with
steps in the path matrix. In our experiments, we use a
simple zero mean Gaussian kernel with standard de-
viation 0.1 as ground kernel. The step weights C
HV
and C
D
are set to 0.3 and 0.34 respectively. We use
the same setting throughout the experiments. The be-
haviour of the kernel will change with the value of
these parameters. A complete analysis of this is how-
ever beyond the scope of this paper. Here, we focus on
the general characteristics of our kernel which sum-
marises all possible paths using step weights satisfy-
ing C
HV
< C
D
– implying a preference for diagonal
paths.
In order to get an understanding of the geomet-
ric configuration of the data that our kernel matrices
corresponds to, we project the three different kernels
onto their first two principal directions in Figure 4. It
is important to note that, as the DTW kernel has neg-
ative eigenvalues, it does not imply a geometrically
valid configuration of datapoints in a feature space.
From Figure 4, we get a qualitative understanding
of how the induced feature spaces looks like. How-
ever, a representation is simply the means to an end
and to be able to make a valuable assessment of its
useability, we need to use it to achieve a task. We do
so through two different experimental set-ups: The
first is meant to test the discriminative capabilities of
the representation; the second evaluates how well the
representation is suited for generalisation.
In order to test the discriminability of the feature
space generated by the path kernel, we perform a clas-
sification experiment using the same data as explained
above, and where the task is to predict the generat-
ing class of a waveform. We feed the kernel matrix
into an SVM classifier (Chang and Lin, 2001), use
a 2-fold cross-validation, and report the average over
50 runs. Due to the negative eigenvalues, the clas-
sification fails for the DTW kernel. For this reason,
we only present results for the remaining two kernels.
In Figure 5, the results for the classification with in-
creasing noise levels are shown. For moderate noise-
levels (up to σ
{l,i,o}
= 5), the global alignment and the
path kernel are comparable in performance, while –
at a higher noise level – the performance of the global
alignment rapidly deteriorates and at σ
{l,i,o}
= 9 its
performance is about chance, while the path kernel
still achieves a classification rate of over 80%.
0.0 0.5 1.0 2.0 3.0 5.0 6.0 7.0 8.0 9.0
Noise σ
0.0
0.2
0.4
0.6
0.8
1.0
Performance
log(k
GA
)
k
P AT H
Figure 5: We display the classification rate for predicting
the waveform type using an SVM classifier in the feature
space defined by the global alignment kernel (blue) and
the path kernel (green). The x-axis depicts the noise level
parametrized by σ
{l,i,o}
.
The classification experiment shows that the path
kernel significantly outperformed the global align-
ment kernel when noise in the sequence became sig-
nificant. Looking at the feature space, depicted in
Figure 4, we see that the path kernel encodes a fea-
ture space having more clearly defined clusters cor-
responding to the different waveforms. Additionally,
the clusters also have a simpler structure. This sig-
nifies that the path kernel should be better suited for
generalisation purposes, where it is beneficial to have
a large continuous region of support which gracefully
describes the variations in the data – rather than work-
ing in a space that barely separates the classes. We
now generate a new dataset consisting of 100 noisy
sine-waves (σ
{l,i,o}
= 5) shifted in phase between 0
and π. The data is split uniformly into two halves and
the first is used for training and the second for test-
ing. We want to evaluate how well the kernel is capa-
ThePathKernel
55

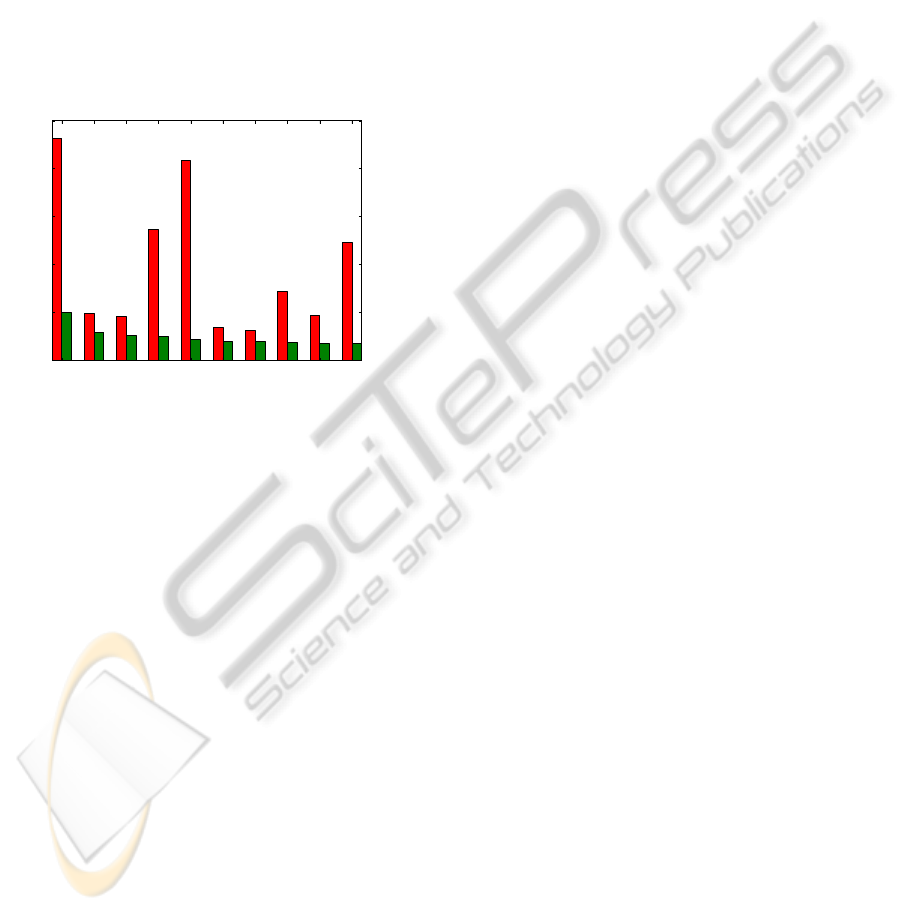
ble of generalising over the training data. To that end
we regress from the proportion of the training data
to the test data and evaluate how the prediction error
changes by altering this proportion. The prediction is
performed using simple least-square regression over
the kernel induced feature space. In Figure 6, the
results are shown using different sizes of the train-
ing data. As shown, the path kernel performs signif-
icantly better compared to the global alignment ker-
nel and the results improve with the size of the train-
ing dataset. Interestingly, the global alignment ker-
nel produces very different results dependent on the
size of the training dataset indicating that it is severely
over-fitting the data.
5 10 15 20 25 30 35 40 45 50
training examples
0
10
20
30
40
50
RMS Error
Figure 6: The above figure depicts the RMS error when
predicting the phase shift from a noisy sine waveform by
a regression over the feature space induced by the kernels.
The red bars correspond to the global alignment kernel and
the green bars to the path kernel. The y-axis shows the error
in percentage of phase, while the x-axis indicates the size of
the training dataset.
5 CONCLUSIONS
In this paper, we have presented a novel kernel for en-
coding sequences. Our kernel reflects and encodes all
possible alignments between two sequences by asso-
ciating a cost to each. This cost encodes a preference
towards specific paths. The kernel is applicable to
any kind of symbolic or numerical data as it requires
only the existence of a kernel between symbols. We
have presented both qualitative and quantitative ex-
periments exemplifying the benefits of the path kernel
compared to competing methods. We show that the
proposed method significantly improves results both
with respect to discrimination and generalisation es-
pecially in noisy scenarios. The computational cost
associated with the kernel is considerably lower than
competing methods, making it applicable to data-sets
that could previously not be investigated using ker-
nels.
Our experimental results indicate that the kernel
we propose is positive semi-definite. In future we
intend to investigate proving this property. Further-
more, in this paper, we have chosen a very simplis-
tic dataset in order to evaluate our kernel. Given
our encouraging results, we are currently working on
applying our kernel to more challenging real-world
datasets.
REFERENCES
Bahlmann, C., Haasdonk, B., and Burkhardt, H. (2002).
Online handwriting recognition with support vector
machines - a kernel approach. In 8th International
Workshop on Frontiers in Handwriting Recognition.
Berlinet, A. and Thomas-Agnan, C. (2004). Reproducing
kernel Hilbert spaces in probability and.
Buhmann, M. D. and Martin, D. (2003). Radial basis func-
tions: theory and implementations.
Chang, C. C. and Lin, C. J. (2001). LIBSVM: a library for
support vector machines.
Cristianini, N. and Shawe-Taylor, J. (2006). An introduction
to support Vector Machines: and other kernel-based
learning methods.
Cuturi, M. (2010). Fast Global Alignment Kernels. In In-
ternational Conference on Machine Learning.
Cuturi, M., Vert, J.-P., Birkenes, O., and Matsui, T. (2007).
A Kernel for Time Series Based on Global Aligh-
ments. In IEEE International Conference on Acous-
tics, Speech and Signal Processing, pages 413–416.
Gudmundsson, S., Runarsson, T. P., and Sigurdsson, S.
(2008). Support vector machines and dynamic time
warping for time series. IEEE International Joint
Conference on Neural Networks, pages 2772–2776.
Haasdonk, B. (2005). Feature space interpretation of SVMs
with indefinite kernels. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 27(4):482–492.
Haasdonk, B. and Burkhardt, H. (2007). Invariant kernel
functions for pattern analysis and machine learning.
Machine learning, 68(1):35–61.
Haussler, D. (1999). Convolution kernels on discrete struc-
tures. Technical report.
Leslie, C. and Kuang, R. (2004). Fast String Kernels using
Inexact Matching for Protein Sequences. The Journal
of Machine Learning Research, 5:1435–1455.
Li, M. and Zhu, Y. (2006). Image classification via LZ78
based string kernel: a comparative study. Advances in
knowledge discovery and data mining.
Lodhi, H., Saunders, C., Shawe-Taylor, J., Cristianini, N.,
and Watkins, C. (2002). Text classification using
string kernels. The Journal of Machine Learning Re-
search, 2:419–444.
Luo, G., Bergstr
¨
om, N., Ek, C. H., and Kragic, D. (2011).
Representing actions with Kernels. In IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems, pages 2028–2035.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
56

Sakoe, H. and Chiba, S. (1978). Dynamic programming
algorithm optimization for spoken word recognition.
IEEE Transactions on Acoustics, Speech and Signal
Processing, 26(1):43–49.
Saunders, C., Tschach, H., and Shawe-Taylor, J. (2002).
Syllables and other string kernel extensions. Proceed-
ings of the Nineteenth International Conference on
Machine Learning (ICML’02).
Sivic, J. and Zisserman, A. (2009). Efficient Visual Search
of Videos Cast as Text Retrieval. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
31(4):591–606.
Watkins, C. (1999). Dynamic alignment kernels. In Ad-
vances in Neural Information Processing Systems.
ThePathKernel
57