Exploiting Correlation-based Metrics to Assess Encoding Techniques

Giuliano Armano and Emanuele Tamponi

Department of Electrical and Electronic Engineering, University of Cagliari, Cagliari, Italy

Keywords:

Supervised Learning, Correlation, Metrics, Performance, Encoding Techniques, Classiﬁcation, Prediction.

Abstract:

The performance of a classiﬁcation system depends on various aspects, including encoding techniques. In

fact, encoding techniques play a primary role in the process of tuning a classiﬁer/predictor, as choosing the

most appropriate encoder may greatly affect its performance. As of now, evaluating the impact of an encoding

technique on a classiﬁcation system typically requires to train the system and test it by means of a performance

metric deemed relevant (e.g., precision, recall, and Matthews correlation coefﬁcients). For this reason, assess-

ing a single encoding technique is a time consuming activity, which introduces some additional degrees of

freedom (e.g., parameters of the training algorithm) that may be uncorrelated with the encoding technique to

be assessed. In this paper, we propose a family of methods to measure the performance of encoding techniques

used in classiﬁcation tasks, based on the correlation between encoded input data and the corrisponding output.

The proposed approach provides correlation-based metrics, devised with the primary goal of focusing on the

encoding technique, leading other unrelated aspects apart. Notably, the proposed technique allows to save

computational time to a great extent, as it needs only a tiny fraction of the time required by standard methods.

1 INTRODUCTION

When facing a difﬁcult classiﬁcation or prediction

task (e.g., protein secondary structure prediction, face

recognition, ﬁngerprint recognition), the corrispond-

ing system must be tuned with great care. Without

loss of generality,let us consider any such system as a

pipeline, consisting of two cascading parts: an encod-

ing module and a classiﬁer/predictor. The encoding

module is fed with input data, so to provide the clas-

siﬁer/predictor with a properly encoded input data, so

to facilitate the learning task.

Choosing a good encoding technique is crucial to

improve the overall performance of a system. How-

ever, to our best knowledge, no speciﬁc methods have

been proposed to assess an encoding technique in iso-

lation from the corresponding classiﬁer/predictor. In

fact, the system is typically considered as a whole,

and the overallperformanceis used as an indirect met-

ric to asses alternative encodings. This standard ap-

proach has some advantages; in particular, it provides

performance estimates of the ﬁnal system. For exam-

ple, precision and recall have clear meaning, as well

as ROC curves and Matthews correlation coefﬁcients.

It can be used to assess encoding techniques, accord-

ing to the following strategy: several systems, which

only differ for the encoding technique, can be tested

separately, giving rise to a comparative table that typ-

ically reports all performance metrics deemed rele-

vant. In presence of enough test data, one may assume

that statistical signiﬁcance holds. Hence, it becomes

viable to assume that, if any changes in the perfor-

mance indices were observed, they should depend on

the encoder. According to the selected performance

metric, one may also generate a ranking of encoders.

Unfortunately,the above strategy has some impor-

tant drawbacks, the main one being that every per-

formance evaluation is highly time consuming, often

making unfeasible the test of many different encoding

techniques. For example, a 10-fold cross validation of

a system based on neural networks devised for protein

secondary structure prediction usually takes several

hours to complete. Now, assuming that the technique

in hand is parametric, ﬁnding the optimal value of the

parameter may require weeks or months to complete

(as, for every value of the parameter, an experiment

should be run). Another drawback is that the encod-

ing technique is not assessed in isolation, being part

of a pipeline. This introduces some degrees of free-

dom that are uncorrelated with the encoder, e.g., the

parameters of the learning algorithm, thus reducing

the conﬁdence about statistical signiﬁcance of exper-

imental results. A trivial solution to this problem is

to increase the number of trials; however, this ends up

308

Armano G. and Tamponi E. (2013).

Exploiting Correlation-based Metrics to Assess Encoding Techniques.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 308-314

DOI: 10.5220/0004267503080314

 SciTePress

with incrementing the computational cost of experi-

ments.

Taking into account all existing drawbacks, it ap-

pears reasonable to look for alternative strategies for

assessing encoding techniques. In this paper, we pro-

pose a new strategy, able to measure the performance

of an encoding technique in isolation from the cor-

responding classiﬁer/predictor. This goal is achieved

by using input-output correlation-based metrics. In

particular, we show that the performance predicted by

these metrics is almost always equal to the actual per-

formance achieved by the encoders under exam when

put in a real pipeline, while the time needed for the

assessment is typically much smaller than the one re-

quired by the standard strategy described above. The

remainder of this work is structured as follows: Sec-

tion 2 introduces the terminology used, describes the

proposed metrics and shows how to use them for as-

sessing encoding techniques; Section ?? reports the

results obtained by applying the proposed metrics to

a speciﬁc problem (i.e., protein secondary structure

prediction); Section ?? concludes the paper and dis-

cusses about future research directions.

2 CORRELATION-BASED

METRICS FOR ASSESSING

ENCODING TECHNIQUES

In this section, after recalling and discussing the main

characteristics of of correlation coefﬁcients and cor-

relation matrices, speciﬁc metrics are described for

evaluating the correlation between input and output

data –under the assumption that inputs are encoded

according to a speciﬁc technique to be assessed.

2.1 Correlation Coefﬁcients and

Correlation Matrices

A correlation coefﬁcient or correlation index is a

quantitativeestimate of the tendency of a variable (the

controlled or dependent variable) to follow the varia-

tion of another variable (the control or independent

variable). In a general setting, correlation does not

imply causal effect; however, assuming that a cause-

effect relationship holds between two random vari-

ables, measuring the correlation between them can

give a hint about how strong this relationship is.

Many correlation coefﬁcients can only be com-

puted between scalar variables (e.g., Pearson product-

moment correlation coefﬁcient). In this case, it is re-

quired to deal with correlation matrices, deﬁned as

follows:

C(X, Y) = [Corr(X

)] i = 1, . . . , n j = 1, . . . , m

where X and Y are vectors of random variables and

and Y

are the i-th and j-th component of X and Y,

respectively. Corr(X,Y) is a correlation coefﬁcient

calculated between two scalar random variables.

When focusing on encoding techniques used in

a classiﬁcation/prediction task, the independent vari-

able X is typically a vector of real values (represent-

ing the encoded input data), whereas the dependent

variable Y is a simple output encoding for the corre-

sponding category. For example, given categories A,

B, and C, we can encode them using one-hot or nu-

meric encoding. In the former case, a possible assign-

ment would be:

A =









B =









C =









whereas in the latter case, a possible assignment

would be:

A = 1 B = 2 C = 3

It is worth noting that one-hot encoding can be

used to turn an m-class classiﬁcation task into m bi-

nary classiﬁcation tasks, one for each component of

the output encoding.

Two correlation matrices will be used exten-

sively hereinafter: the input-input correlation matrix

C(X, X), denoted as C

, and the input-output cor-

relation matrix C(X, Y), denoted as C

. Note that

is always a symmetric semi-deﬁnite positive n× n

square matrix, whereas the number of columns of

depends on the chosen output encoding.

More deﬁnitions follow, concerning the coefﬁ-

cients that have been used in the metrics proposed

hereinafter. Although some of them are very well

known, they are also reported for the sake of com-

pleteness and to clarify the notation used throughout

the paper.

2.1.1 Pearson Product-moment Correlation

Coefﬁcient

Also known as linear correlation coefﬁcient, it is in-

tended to measure the strength of a linear relationship

between two variables:

ρ(X,Y) =

Cov(X,Y)

Var(X)Var(Y)

where Cov(X,Y) and Var(X) denote the covariance

between X and Y and the variance of X, respectively.

ExploitingCorrelation-basedMetricstoAssessEncodingTechniques

309

An estimate of ρ(X,Y), say r, can be obtained from a

sample of N observations:

r =

∑

i=1

−

X)(Y

−

∑

i=1

−

∑

i=1

−

(1)

2.1.2 Correlation Ratio

Originally introduced by Fisher (Fisher, 1925) using

another notation, the correlation ratio can also be de-

ﬁned as:

(X|Y) =

Var[E(X|Y)]

Var(X)

where E(X|Y) denotes the expected value of X given

that Y has been observed. When Y can only assume

discrete values, the correlation ratio can be interpreted

as the ratio between the intraclass dispersion of X and

its overall dispersion. It can be shown (Lewandowski

et al., 2007) that:

(X|Y) = max

f(X)

( f(X),Y)

that is, η equals the linear correlation between Y and

an unknown function of X. Hence, the correlation ra-

tio can be used to highlight non-linear relationships

between variables. An estimate of η

on a sample of

N observations is:

≈

∑

(

−

∑

i=1

−

SSH

SSE

(2)

where n

is the number of observations that fall in the

category y, SSH =

∑

(

−

is the so called “be-

tween sum of squares” and SSE =

∑

i=1

−

the “within sum of squares”.

2.1.3 Wilks’ Generalized Correlation Ratio

The correlation ratio is a powerful coefﬁcient; how-

ever, it can be used only when X is a scalar. There are

many generalizations of this concept to the multivari-

ate case (see, for example (Rencher, 2002)), that is,

when X is a vector of random variables.

Let us ﬁrst deﬁne the “within sum of squares ma-

trix”, E, and the “between sum of squares matrix”, H:

E =

∑

i=1

−

∑

y·

H =

∑

y·

−

··

where N is the total number of samples, n

is the num-

ber of samples that fall in category y, x

y·

is the mean of

all the samples in category y and x

··

is the mean over

all the samples. Let us deﬁne the vector of non-null

eigenvalues of E

−1

H as

(λ

, λ

, . . . , λ

) = eig(E

−1

where λ

≥ λ

≥ . . . ≥ λ

. We can now deﬁne Wilks’

Lambda as:

Λ =

∏

i=1

1+ λ

from which we calculate Wilks’ generalized η

= 1− Λ

2.2 Devising Correlation-based Metrics

for Assessing Encoding Techniques

Be X a random variable whose sample x

is the encod-

ing of the i-th training sample taken from a training set

of N labeled data instances. Accordingly, the samples

of the random variable Y, are the output encoding

of the label associated with x

After selecting a particular correlation coefﬁcient,

and C

must be evaluated

. Unfortunately,these

correlation matrices contain too many data to be used

directly as a metric for assessing the performance of

an encoding technique. For this reason, a procedure

for extracting one or more synthetic values from these

matrices must be devised.

According to this view, we deﬁne a correlation-

based metric as a method for extracting one or more

synthetic values from the input-inputand input-output

correlation matrices, with the goal of predicting the

performance of the encoding technique under test. In

symbols:

m(E) := m(C

, C

)

where E represents the encoding technique. The di-

mension of the metric vector m(E) is determined by

the output encoding used to calculate C

; i.e.:

(E) = m

· j

, C

)

where the synthetic value m

(E) is a function of the j-

th column of the input-output correlation matrix c

· j

and of the input-input correlation matrix C

. Using

the output encodings recalled in Subsection 2.1 let us

now deﬁne two kinds of metrics:

• if the output encoding is one-hot, m

(E) extracts

information from the correlation between the in-

put encoding and the j-th label. The correspond-

ing metric is a one-hot metric, denoted as m

Except for the case of the generalized correlation ratio.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

310

• if the output encoding is numeric, m(E) has only

one component; hence, m(E) = m(E). We call

this metric a numeric metric, denoted as m

num

In order to obtain a validm

(E), this function should

obey two basic rules:

• Input-output Correlation: if two encodings have

the same C

and c

· j

, except for a speciﬁc c

then the one that has the higher input-output cor-

relation will also perform better than the other.

• Input-input Correlation: if two encoding have

the same C

and c

· j

, except for a single c

, then

the one with higher input-input correlation will

perform worse than the other (in so doing, the re-

dundancy of input encoding components can be

properly taken into account).

In practice, two different synthetic value functions

have been devised:

2.2.1 Max-sum Segment Function

mss

· j

, C

) = (1− β)

∑

i=1

| + β max

i=1,...,n

(3)

where:

β = α

0 < α ≤ 1

n(n− 1)

∑

i=1

∑

j=i+1

Notably,

is the mean value of the input-input

correlation matrix (as it is symmetric), and α is a pa-

rameter that regulates the dependence of m

(E) from

To understand why m

mss

deﬁnes a metric for E,

we should consider the following cases:

•

= 0, we infer the absence of redundancy in

the input encoding (in other words, total indepen-

dence holds). In this case, the value of m

mss

∑

i=1

|, so it equals the sum of the correla-

tion values between each component of the input

and the j-th output. If no redundancy in the input

encoding is observed, the value of the synthetic

function grows with each component of the input-

output correlation.

•

= 1, we observe that the components of the

input encoding are completely correlated with

each other (in other words, total redundancy

holds). This means that the same information

can be obtained by just removing all the com-

ponents but one. In particular, we preserve the

one that maximizes the input-output correlation:

max

i=1,...,n

• 0 < C

< 1, we expect the synthetic value be

somewhere in the middle between total redun-

dancy and total independence of the input encod-

ing components. For this reason, m

mss

assumes a

value in the segment deﬁned by the two extreme

points described above, moving toward one end or

the other, depending on the value of C

2.2.2 Multiple Determination Coefﬁcient

· j

, C

) =

· j

)

−1

· j

) (4)

When correlation is computed using Pearson’s

formula, the term under square root is the multiple

correlation coefﬁcient R

, but m

can be calculated

for any C

that is positive deﬁnite. This function can

be seen as a weighted scalar product of the input-

output correlation vector c

· j

. The inverse of the

input-input correlation matrix has the role of weight-

ing the various components of the input-output vector

in order to take into account redundancy between the

components of the input encoding.

3 EXPERIMENTAL RESULTS

3.1 Domain: Protein Secondary

Structure Prediction

We have tested correlation-based metrics in the

ﬁeld of protein secondary structure prediction (SSP),

which characterises itself as a complex learning prob-

lem. This research ﬁeld is particularly suitable for

assessing the proposed metrics, as various encoding

techniques have been proposed in literature, and ex-

perimental results show that the performance of a sec-

ondary structure predictor is highly dependent on the

adopted encoding technique.

Moreover, the standard strategy (i.e., k-fold cross

validation) appears not suitable due to the following

computational problems:

• secondary structure prediction is typically per-

formed with ensembles of stacked multilayer neu-

ral networks (see, for instance, (Jones, 1999)). As

each neural network embodies hundreds of input

neurons and tens of hidden layer neurons, assess-

ing a single encoding technique by means of a

standard strategy, on a speciﬁc setting of a speciﬁc

architecture, is computationally expensive (from

hours to days of training, depending on the avail-

able computing power);

ExploitingCorrelation-basedMetricstoAssessEncodingTechniques

311

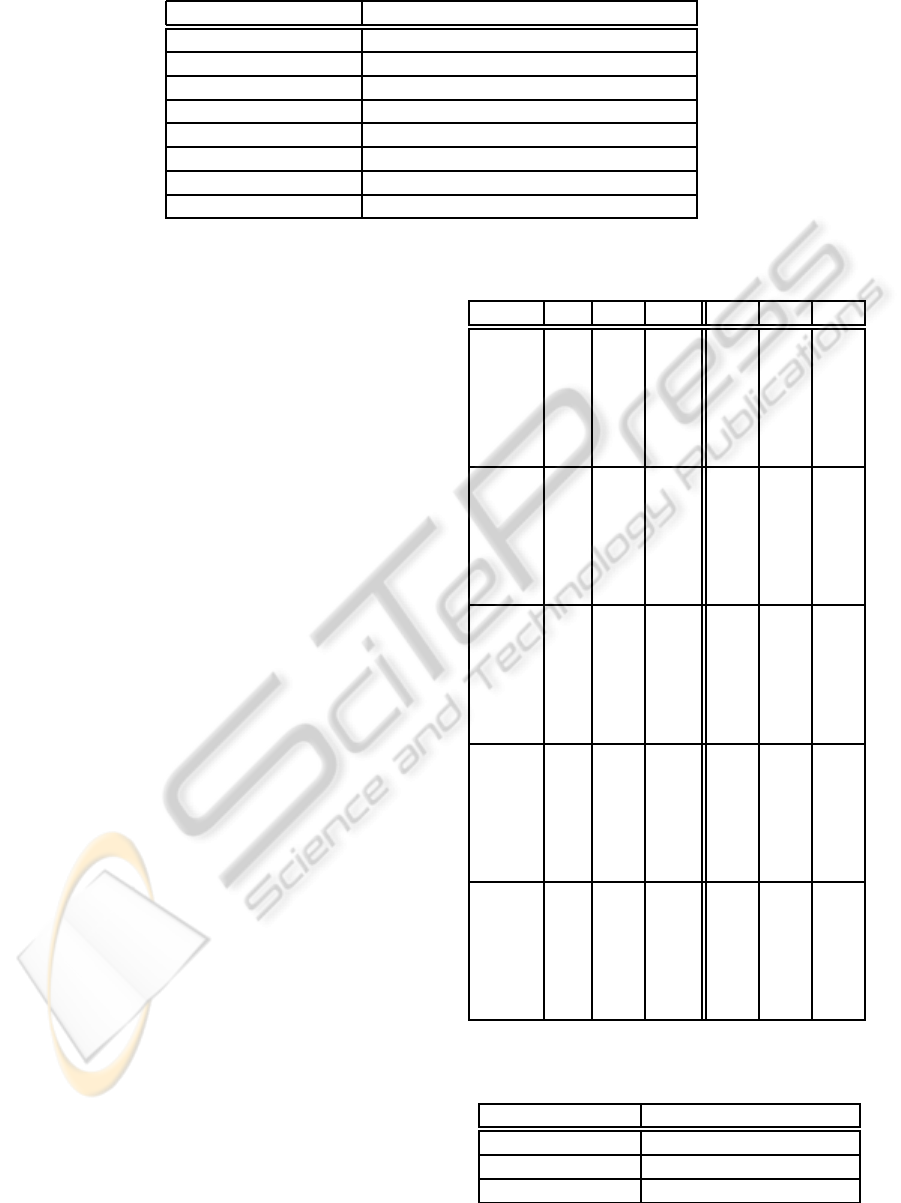
Table 1: Parameters for 10-fold cross validation.

Parameter Value

Complete dataset 3326 non redundant (¡ 25%) sequences

Total test sequences 700 at random

Hidden layer neurons 75

Max iterations 1000

Momentum 0.1

Learning rate 0.001

Validation % 10% (of the training set for each fold)

Stop after 30 iterations without improvements

• the prediction task is typically turned into a clas-

siﬁcation task by splitting the target protein into

ﬁxed-length slices obtained by means of a sliding

window. In doing so, each encoding becomes in

fact parametric, the parameter being the size of the

sliding window. Hence, the problem of ﬁnding an

optimal windowsize grows linearly with the num-

ber of values that the parameter can take. In other

words, the adopted standard strategy (e.g., based

on k-fold cross validation) must be repeated for

each value of the parameter.

3.2 Experimental Settings

Experiments have been performed using ﬁve differ-

ent encoding techniques: One Hot on the primary

structure (PSOH), Blosum Score Matrix (Henikoff

and Henikoff, 1992) (SCMA), PSI-BLAST Position-

Speciﬁc Scoring Matrix (Altschul et al., 1997)

(PSSM), Frequencies (Rost, 1996) (FREQ), and Sum

Linear Blosum (SLBL). For each encoding, six dif-

ferent window sizes have been tested (1, 5, 9, 13, 17,

and 21), for a total of 30 different settings.

The overall indices have been calculated with 10-

fold cross validation on a multilayer neural network,

using the parameters shown in Table 1. Table 2 shows

accuracy (called Q

in the ﬁeld of secondary structure

prediction), SOV (Rost et al., 1994) and Matthews

correlation coefﬁcients for every setting.

Using the parameters shown in Table 3, three dif-

ferent correlation-based metrics have been calculated:

• Multiple Determination Metric (MDM): correla-

tion matrices are calculated using Equation 1,

whereas the synthetic value is evaluated accord-

ing to the function deﬁned by Equation 4.

• Correlation Ratio with Max-Sum Segment syn-

thetic value function (CR-MSS): input-input cor-

relation matrix is calculated with Pearson coefﬁ-

cient, input-output correlation matrix using Equa-

tion 2, whereas the synthetic value is evaluated

according to the function deﬁned by 3.

Table 2: Performance evaluated with 10-fold cross valida-

tion (WS = window size).

Enc. WS Q

SOV C

PSOH

1 51.3 34.5 13.0 25.5 14.0

5 62.2 55.4 33.7 24.9 35.7

9 64.6 59.4 40.5 29.8 38.9

13 66.4 61.4 43.9 32.0 40.2

17 66.1 60.5 44.3 33.3 39.7

21 65.9 59.6 43.3 31.5 38.8

SCMA

1 52.1 36.9 13.6 16.2 14.5

5 62.1 55.2 33.2 25.4 35.0

9 66.0 60.8 41.7 31.4 40.1

13 66.8 62.1 45.0 34.8 40.6

17 67.6 62.8 46.6 36.3 41.2

21 67.0 61.7 45.8 35.2 40.9

FREQ

1 56.5 42.4 31.0 30.6 29.2

5 68.1 60.8 53.5 47.6 48.8

9 71.4 65.0 59.6 52.9 52.2

13 72.6 67.2 62.3 55.0 53.3

17 72.5 66.6 62.7 55.7 53.0

21 72.3 66.7 62.3 56.0 52.7

SLBL

1 58.3 45.6 33.3 31.0 31.5

5 69.0 63.6 54.4 48.3 50.5

9 72.3 68.0 61.0 53.9 54.0

13 74.5 71.2 64.4 58.1 55.2

17 74.7 71.4 65.3 58.4 55.4

21 74.7 71.1 64.7 58.2 55.3

PSSM

1 57.2 43.2 31.9 27.4 30.3

5 69.0 62.7 55.0 48.4 50.3

9 72.1 66.7 61.2 53.8 53.6

13 74.0 69.2 64.2 57.2 54.7

17 74.0 69.1 64.0 57.8 54.6

21 73.9 69.1 64.0 57.1 54.5

Table 3: Parameters used to calculate correlation-based

metrics.

Parameter Value

Complete dataset Same as cross validation

Total runs 10

Samples per run 10000

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

312

• Wilks’ Correlation Ratio Metric (WCRM): no cor-

relation matrices are required, as Wilks’ general-

ized correlation ratio is already a scalar value.

Table 4: Performance measured with MDM.

Enc. WS m

num

PSOH

1 8.0 5.0 5.0 8.0

5 23.0 16.0 15.0 23.0

9 24.0 22.0 22.0 27.0

13 28.0 25.0 24.0 28.0

17 30.0 28.0 24.0 30.0

21 31.0 30.0 27.0 32.0

SCMA

1 8.0 5.0 6.0 8.0

5 23.0 18.0 17.0 24.0

9 25.0 24.0 21.0 28.0

13 27.0 27.0 23.0 29.0

17 29.0 29.0 25.0 31.0

21 30.0 30.0 27.0 32.0

FREQ

1 12.0 10.0 10.0 13.0

5 30.0 30.0 28.0 32.0

9 33.0 38.0 33.0 36.0

13 35.0 41.0 36.0 38.0

17 37.0 43.0 37.0 39.0

21 38.0 44.0 39.0 40.0

SLBL

1 15.0 14.0 13.0 16.0

5 33.0 35.0 32.0 35.0

9 36.0 42.0 36.0 39.0

13 38.0 45.0 39.0 40.0

17 39.0 47.0 41.0 42.0

21 40.0 48.0 42.0 43.0

PSSM

1 16.0 16.0 14.0 17.0

5 33.0 37.0 33.0 35.0

9 36.0 43.0 37.0 38.0

13 37.0 45.0 40.0 39.0

17 39.0 47.0 41.0 41.0

21 40.0 48.0 42.0 42.0

Tables 4, 5, and 6 show the performances esti-

mated using the above metrics. Note that, depending

on the selected output encoding, the metric that eval-

uates the input encoding technique gives rise to either

a single value (numeric metric, m

num

) or to a vector of

values (one-hot metric, m

, m

, and m

), as discussed

in 2.2.

3.3 Assessment of Correlation-based

Metrics

The performances estimated with the proposed met-

rics have been compared with those measured using

10-fold cross validation. In particular, Spearman’s ρ

correlation coefﬁcient has been used to understand to

which extent the ranking generated by a correlation-

based approach predicts the ranking found by running

Table 5: Performance measured with CR-MSS.

Enc. WS m

num

PSOH

1 4.0 5.0 23.0 24.0

5 24.0 23.0 73.0 84.0

9 33.0 35.0 81.0 92.0

13 42.0 43.0 94.0 104.0

17 44.0 48.0 101.0 112.0

21 54.0 53.0 104.0 112.0

SCMA

1 5.0 5.0 23.0 27.0

5 23.0 23.0 73.0 86.0

9 35.0 35.0 81.0 96.0

13 43.0 43.0 94.0 109.0

17 48.0 48.0 101.0 117.0

21 53.0 53.0 104.0 122.0

FREQ

1 29.0 10.0 16.0 18.0

5 96.0 44.0 48.0 53.0

9 124.0 65.0 60.0 61.0

13 145.0 77.0 71.0 69.0

17 158.0 85.0 78.0 74.0

21 166.0 90.0 81.0 77.0

SLBL

1 58.0 9.0 38.0 42.0

5 198.0 44.0 120.0 137.0

9 240.0 68.0 137.0 162.0

13 283.0 85.0 158.0 187.0

17 313.0 101.0 169.0 208.0

21 335.0 115.0 174.0 224.0

PSSM

1 57.0 11.0 37.0 39.0

5 196.0 52.0 117.0 128.0

9 241.0 80.0 139.0 146.0

13 280.0 96.0 164.0 162.0

17 303.0 107.0 177.0 171.0

21 316.0 116.0 183.0 175.0

experiments by means of actual predictors (see Table

7).

Results show how Wilks’ correlation ratio metric

and multiple determination metric are almost com-

pletely correlated with the experimental results ob-

tained by running 10-fold cross validation. This result

makes them suitable for identifying the best encoding

technique among a set of candidates, without the need

to run time-consuming tests.

As for Table 8 highlights the speed-up obtained by

using the proposed approach versus 10-fold cross val-

idation (whose settings are reported in Table 1). Re-

sults clearly show that the latter strategy can be 300

times slower than the former.

ExploitingCorrelation-basedMetricstoAssessEncodingTechniques

313

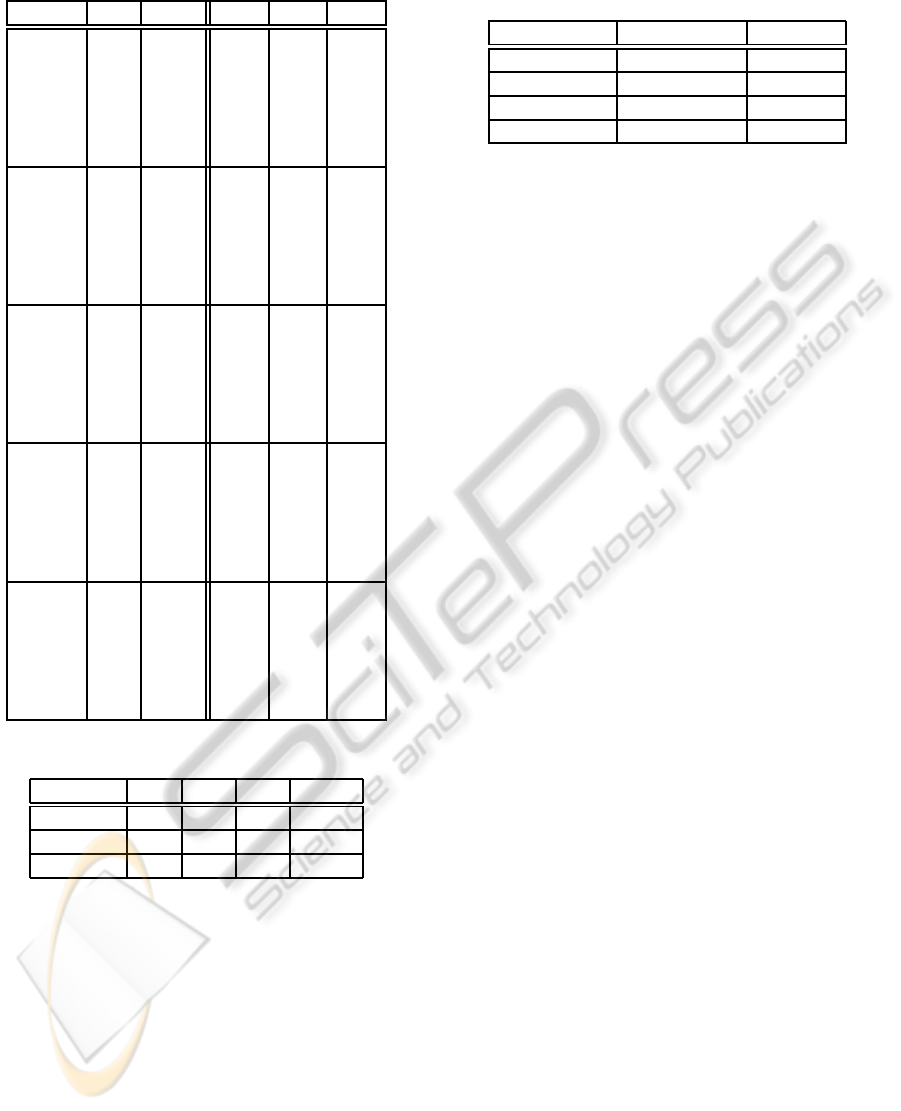
Table 6: Performance measured with WCRM.

Enc. WS m

num

PSOH

1 13.0 5.0 5.0 8.0

5 34.0 19.0 16.0 24.0

9 40.0 22.0 20.0 28.0

13 44.0 28.0 22.0 29.0

17 46.0 30.0 24.0 31.0

21 51.0 28.0 26.0 32.0

SCMA

1 12.0 5.0 6.0 8.0

5 35.0 18.0 17.0 24.0

9 42.0 24.0 21.0 28.0

13 46.0 27.0 23.0 29.0

17 48.0 29.0 25.0 31.0

21 50.0 30.0 27.0 32.0

FREQ

1 21.0 10.0 10.0 13.0

5 51.0 30.0 28.0 32.0

9 58.0 38.0 33.0 36.0

13 61.0 41.0 36.0 38.0

17 63.0 43.0 37.0 39.0

21 65.0 44.0 39.0 40.0

SLBL

1 26.0 14.0 13.0 16.0

5 56.0 35.0 32.0 35.0

9 63.0 42.0 36.0 39.0

13 66.0 45.0 39.0 40.0

17 68.0 47.0 41.0 42.0

21 69.0 48.0 42.0 43.0

PSSM

1 29.0 16.0 14.0 17.0

5 57.0 37.0 33.0 35.0

9 63.0 43.0 37.0 38.0

13 66.0 45.0 40.0 39.0

17 68.0 47.0 41.0 41.0

21 69.0 48.0 42.0 42.0

Table 7: Spearman’s ρ

Metric ρ

S,h

S,e

S,c

S,num

MDM 98 87 96 98

CR-MSS 92 65 76 92

WCRM 98 87 96 98

4 CONCLUSIONS AND FUTURE

WORK

In this paper, a family of methods to measure the per-

formance of encoding techniques used in classiﬁca-

tion tasks has been presented, based on correlation

between encoded input data and the corresponding

output. The proposed approach provides correlation-

based metrics, devised with the primary goal of focus-

ing on the encoding technique to be assessed, leading

other unrelated aspects apart. Experimental results

clearly show that the proposed approach is far more

Table 8: Time required to run the experiments described

above.

Strategy Average time Speed-up

10-fold x-val ∼90 -

MDM ∼8 10x

CR-MSS ∼5 18x

WCRM ∼0.3 300x

efﬁcient than a standard approach based on repeat-

edly training and testing classiﬁers or predictors with

different encodings. No apparent drawbacks have

been identiﬁed so far with the proposed strategy, as

the rankings obtained with correlation-based metrics

almost perfectly ﬁt the ones obtained with standard

strategies. Moreover, a very high speed-up has been

achieved, making a step further in the task of ﬁnding

an optimal encoding for speciﬁc and complex learn-

ing problems.

Future research directions are: i) applying the pro-

posed metrics to encoding techniques frequently used

in well-known and complex learning tasks; ii) de-

vising rules aimed at selecting the right metrics ac-

cording to the speciﬁc encoding to be assessed; and

iii) studying the possibility of using correlation-based

metrics in a framework for feature selection and ex-

traction.

REFERENCES

Altschul, S. F., Madden, T. L., Sch¨affer, A. A., Zhang,

J., Zhang, Z., Miller, W., and Lipman, D. J. (1997).

Gapped BLAST and PSI-BLAST: a new generation

of protein database search programs. Nucleic acids

research, 25(17):3389–3402.

Fisher, R. (1925). Statistical methods for research workers.

Edinburgh Oliver & Boyd.

Henikoff, S. and Henikoff, J. G. (1992). Amino acid sub-

stitution matrices from protein blocks. Proceedings of

the National Academy of Sciences of the United States

of America, 89(22):10915–10919.

Jones, D. T. (1999). Protein secondary structure prediction

based on position-speciﬁc scoring matrices. Journal

of molecular biology, 292(2):195–202.

Lewandowski, D., Cooke, R. M., and Tebbens, R. J. D.

(2007). Sample-based estimation of correlation ratio

with polynomial approximation. ACM Trans. Model.

Comput. Simul., 18(1):3:1–3:17.

Rencher, A. C. (2002). Methods of Multivariate Analysis.

John Wiley & Sons, second edition.

Rost, B. (1996). Phd: predicting one-dimensional protein

structure by proﬁle based neural networks. Methods

in Enzymology, 266:525–539.

Rost, B., Sander, C., and Schneider, R. (1994). Redeﬁn-

ing the goals of protein secondary structure prediction.

Journal of Molecular Biology, 235(1):13 – 26.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

314