
Graph-based Shape Representation for Object Retrieval
Ali Amanpourgharaei, Christian Feinen and Marcin Grzegorzek
Research Group for Pattern Recognition, University of Siegen, Holderlinstr. 3, Siegen, Germany
Keywords: Graph-based Shape Representation, Shape Description, Shape Similarity Measure, Image Retrieval.
Abstract: Shape analysis has been an area of interest and research in image processing for a long time. Developing a
discriminant shape representation and description method is a concern in many applications like image
retrieval systems. This paper presents a new shape representation model which is based on graphs. We also
present developed similarity measure technique to find correspondences between shapes. In our approach,
features extracted from boundary of the shape are used to build up a graph. By means of a novel solution for
attributed graph matching a new method for shape similarity measure is built up.
1 INTRODUCTION
There is little doubt that researches related to main
human sense or vision are among the most recent
stimulating research fields. Effective computer
vision systems are essential whenever necessary to
automate or to improve. Within recent years object
recognition has become a fundamental and
challenging problem in computer vision.
There are different properties like shape, texture,
colour, etc. used in object recognition. Among those
features, shape is most effective in semantically
characterizing the object and one can be perceived
and used for recognition and classification tasks
(Daliri and Torre, 2010). Shape representation is a
very important issue in computer vision and pattern
recognition. Using the shape of an object for object
recognition and image understanding are expanding
topics in computer vision and multimedia
processing. Hence, finding powerful shape
descriptors and matching measures are the central
issues in these applications (Xu et al., 2009).
This paper discribes the result of investigating a
new model for shape representation based on graphs
and new similarity measure technique to find
correspondences between different shapes in the
proposed methodology. Discrete curve evolution
(DCE) algorithm (Bai et al., 2007) is employed to
find important points of the shape’s boundary, which
has been simplified by polygonal approximation.
Features extracted from these points are stored in a
graph representing the shape. To find the similarity
between shapes, a new attributed graph matching
algorithm exploiting dynamic programming has
been developed. Our approach is invariant to affine
transformation and can handle partial occlusion.
Moreover, it is low computationally complex that is
very important in retrieval systems.
The paper is organized as follows: in Section 2
related works are discussed. Section 3 introduces a
novel graph-based shape representation and shape
similarity measure technique. Section 4 is dedicated
for evaluation of our approach and discussion about
the result. Finally, in Section 5 this work is
summarized by conclusion as well as discussion
concerning the future work.
2 RELATED WORKS
Several authors have already proposed methods for
shape representation. Some early works tried to use a
polygonal approximation for shape representation.
Maes (1991) represented a shape by polygon and
proposed a cyclic string matching technique for
polygonal shape recognition. However, the proposed
cost function to measure similarity is not robust
enough. Tan et al., (2008) used equilateral polygonal
approximation for shape representation. However,
they did not propose a solution to find similarity
measure based on their technique.
Probably the most relevant work to this paper has
been proposed by Bai and Latecki (2008). They
represent a shape by skeleton pruned using DCE
(Bai et al., 2007) to remove useless branches. DCE
algorithm selects important points of the skeleton
315
Amanpourgharaei A., Feinen C. and Grzegorzek M. (2013).
Graph-based Shape Representation for Object Retrieval.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 315-318
DOI: 10.5220/0004267703150318
Copyright
c
SciTePress
lying on the contour. The detained points are in fact
vertices of the polygon in our approach. To compare
the shapes, instead of geometric features, they use
geodesic paths between skeleton endpoints. The
result of applying their algorithm on Kimia 216
dataset demonstrates its robustness. However,
skeleton matching involves high degree of
computation (Bai and Latecki, 2008) and their
approach is not suitable for fast recognition.
Another approach which is comparable to our
approach is work of Berretti et al., (2000). In this
method the curvature zero-crossing points from a
Gaussian smoothed boundary are used to obtain
some primitives, called tokens. The feature for each
token is its maxi-mum curvature and its orientation.
Similarity between two tokens is measured by the
weighted Euclidean distance. Since the feature
includes curve orientation, it is not rotation
invariant. Matching of tokens also involves
thresholding which is chosen empirically.
3 SHAPE REPRESENTATION
AND MATCHING
In this Section we explain our approach for graph-
based shape representation and matching. First, the
graph-based model which stores extracted shape’s
features will be discussed. Then we introduce the
technique developed to measure shape similarity,
based on the proposed model
3.1 Graph-based Shape Representation
Many of presented techniques in literature for
contour based shape representation are either
complex (Bai and Latecki, 2008) or not invariant to
rotation, scale and translation. Moreover, none of
them are suitable to describe and represent complex
shapes which include more than one contour.
We exploit the graphs ability to describe
structured data and relation of information to
represent the shape. Our approach to model a shape
by a graph consists of extracting important
information of the shape’s contour and storing them
in a graph. Nodes of this graph correspond to
selected points of the boundary. To assure that
extracted features carry all spatial information of the
shape, in this work we consider some simple shapes,
uniformly filled areas enclosed by contours.
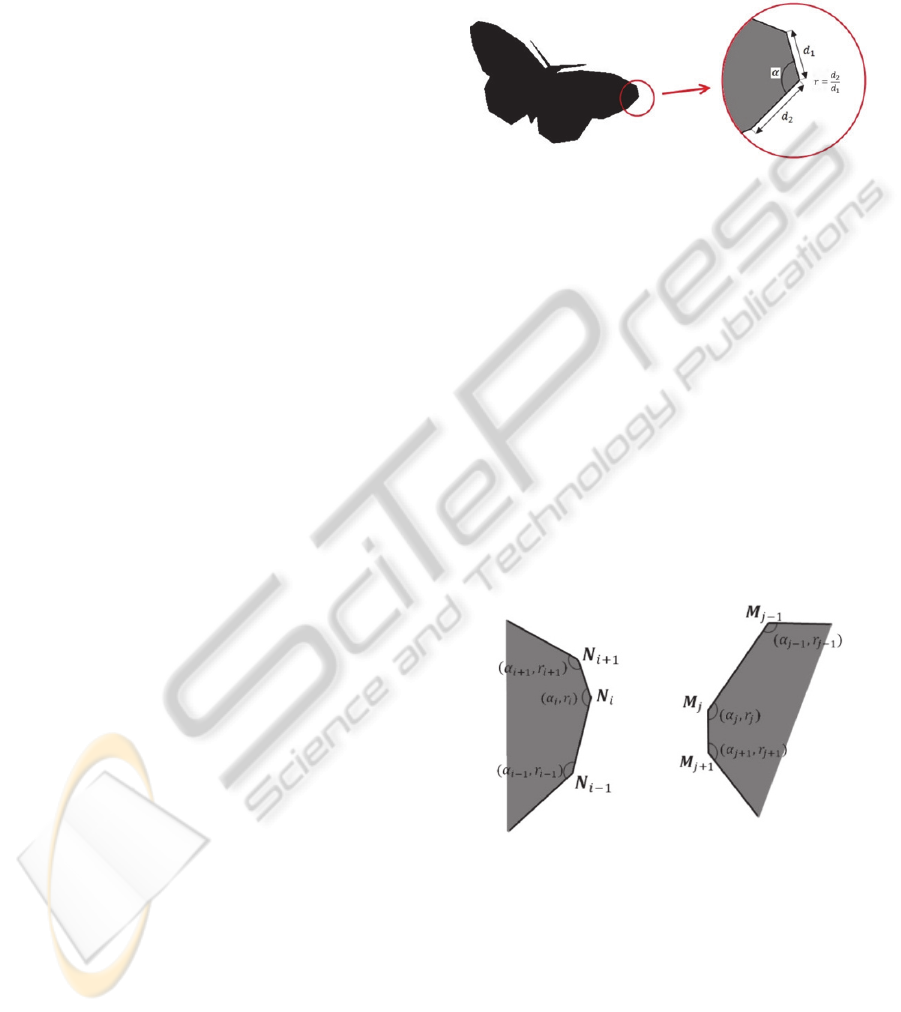
In our approach two attributes of a vertex of
polygon are selected so that they are invariant to
rotation, scale and translation, and are able to
completely characterize such kind of shapes. These
two attributes are interior angle α of each corner and
ratio r of the longer side to the shorter side of it.
These two attributes are depicted in Figure 1. These
two parameters are stored as attributes for each
vertex in an attributed graph.
Figure 1: Internal angle and ratio of longer side to shorter
side are two attributes of each vertex.
3.2 Shape Similarity Measure
Developing a shape similarity measure technique
based on the presented graph-based model
constitures the main part of our research.
Consider the similarity measure between two
nodes
and
from two different shapes (Figure
2), measuring distance between two feature vectors
and
is insufficient. The problem is that after
polygonal approximation, possibility of finding
similar corners among two shapes having similar
values for angle and ratio is high. Therefore some
other parameters increasing the robustness of the
error function to discriminate between similar areas
of two contours are needed.
Figure 2: Indexed vertices in two parts of different shapes
with attributes of each vertex. Neighbours are involved in
measuring similarity between
and
.
To find the new similarity measure and error
function, some experiments have been carried out.
Therefore, a range of different vertices has been
generated (Figure 3). The slight changes between
vertices in the prepared database have been
analysed. Then the required function and parameters
have been found. Carried out experiments revealed
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
316

that attributes of the neighbours are also important to
measure similarity between two areas.
Figure 3: Increasing dissimilarity by gradual changes of
the interior angle and side’s ratio.
To measure the distance between two feature
vectors, Euclidean norm is used. The difference
between two feature vectors is then formulated as:
(1)
Where,
is a constant factor balancing the
unknown influence of interior angel and side’s ratio.
The error function that includes measure of
difference between feature vectors of the two target
corners
and
as well as parts to involve their
neighbors in similarity measure is formulated as
follows:
∆
,
∆
,
(2)
Equation 2 consists of two main parts. First part is a
weighted difference between feature vectors of the
two target corners
and
. The second part is a
weighted sum of difference between two angels
adjacent to the target nodes (∆
,
, ∆
,
).
Experiments showed that using attributes of more
than two neighbours does not improve the result
significantly and just increase the computational
complexity.
The problem of finding correspondences between
two attributed graphs is a typical assignment
problem and it can be solved using Hungarian
algorithm. Unfortunately this algorithm cannot be
used to find the correspondences between two
shapes described by proposed error function because
it does not preserve the order of the match. This is
not acceptable in finding correspondences between
two shapes because the contour of each shape is an
ordered sequence of points. It means that, assuming
that two similar shapes, their correspondences also
have the same order. Therefore, we need to develop
another solution to this problem.
To explain our approach to solve the assignment
problem, consider we have two graphs 1 and 2
with and nodes respectively and we want to find
correspondences between their nodes. The
computational complexity of the algorithm is
. Usually this problem is NP hard. However,
the solution can be found exploiting dynamic
programming as well as applying additional criteria:
1. For each node
of graph 1, a node
of
graph 2 is acceptable as a correspondence, when
the value of error function is lower than a specific
threshold. This threshold indicates minimum
similarity between two nodes and is determined
experimentally.
2. Node
can be selected as a correspondence to
if it preserves the order of nodes of 2 which are
selected as acceptable matches for nodes of 1.
Based on these two rules and exploiting dynamic
programming we solved the problem searching for
longest sequence among candidate nodes for
matching. In the case that longest sequence is not
unique, we use path error: which can helps us to
select best solution among all valid ones.
(3)
This equation helps us to select the best solution
among all valid answers.
4 EXPERIMENTS AND RESULTS
Among various applications of shape representation
and matching, retrieval systems became very
important and popular during last decade (Desai et
al., 2007). One of the most popular methods to
evaluate the discrimination power of shape
representation models and similarity measure
techniques is to use them within a retrieval system.
To have an accurate evaluation of our method we
used Kimia 216 dataset (Sebastian et al., 2004). The
dataset consists of 216 shapes from 18 different
categories and for each category there are 12 images.
Figure 4: Result of finding correspondences between two
similar shapes.
To the discriminant performance of our
Graph-basedShapeRepresentationforObjectRetrieval
317

algorithm, all images in the dataset were used as
query and system searched for similar shapes among
other shapes of the dataset. Considering the fact that
each class consists of 12 images, 11 closest matches
to the query image were considered to see if they
belong to the same class as the query image. The
results of this investigation are illustrated in Table 1.
Table 1: Result of retrieval system using our model on
Kimia 216 dataset.
1
st
2
nd
3rd
4
th
5
th
Result 179 161 148 137 128
6
th
7
th
8
th
9
th
10
th
11
th
118 108 103 87 71 74
In this table, from left to right, correct positive
matches to all queries are sorted. First column
represents the best matches for all the queries. It
indicates that by selecting all 216 shapes as query,
for 179 of them, the best match was correct and for
37 of them the best match was false positive. The
positive feature of our approach which is
comparable to other methods is low computational
complexity. Unfortunately there is no feedback
about computational complexity of the other
methods and therefore comparison of computational
performance between them and our method is not
possible. However, by considering that average time
to find similar shapes of a query in our method is
less than 7 seconds (in a system with Intel Core Due
2 cpu and 4 GB ram), it seems that none of existing
approaches is comparable to it.
5 CONCLUSIONS AND FUTURE
WORKS
In this work three main issues are investigated. First,
the novel graph-based model for shape
representation is discussed. Then, the new technique
for measuring shape similarity is introduced and
finally the robustness of the model and similarity
measure technique is explained and verified using a
retrieval system.
In conclusion, evaluation of this method for
shape representation and results obtained by testing
shape similarity measure technique reveal the
potential power of this method for shape recognition
applications. A promising characteristic of our
method is good recognition speed which shows that
developing this method can lead to establish a fast
and robust technique for online applications.
Probably the main development possibility of
this work is applying this method for complex and
3D shape analysis. As mentioned, this type of shape
representation can be very helpful to describe
complex shapes which are composed of more than
one contour. The possibility to use this technique for
3D shape analysis can be also investigated.
Acknowledgment
ACKNOWLEDGEMENTS
This work was funded by the German Research
Foundation (DFG) as part of the Research Training
Group GRK 1564 "Imaging New Modalities".
REFERENCES
Daliri, M., Torre, V., 2010. Shape recognition based on
Kernel-edit distance. In Computer Vision and Image
Understanding 114, 1097–1103.
Xu, C, Liu, J., Tang, X., 2009. 2D Shape matching by
contour Flexibility. In IEEE Transaction on Pattern
Analysis and Machine Intelligence 31(1).
Maes, M., 1991. Polygonal Shape Recognition Using
String Matching Techniques. In Pattern Recognition
24(5), 433 – 440.
Tan, W., Zhao, S., Wu, C., Li, C., 2008. A Novel
Approach to 2-D Shape Representation Based on
Equilateral Polygonal Approximation. In International
Conference on Computer Science and Software
Engineering.
Bai, X., Latecki, L. J., 2008. Path similarity skeleton graph
matching. In IEEE Trans. Pattern Analysis and
Machine Intelligence 30(7), 1282 – 92.
Bai, X., Latecki, L. J., Liu, W., 2007. Skeleton Pruning by
Contour Partitioning with Discrete Curve Evolution.
IEEE Trans. In Pattern Analysis and Machine
Intelligence 29(3), 449 – 462.
Berretti, S., Bimbo, A. D., Pala, P., 2000. Retrieval by
shape similarity with perceptual distance and effective
indexing. In IEEE Trans. on Multimedia 2(4), 225 –
239.
Desai, P., Pujari, J, Parvatikar, S., 2007. Image Retrieval
using Shape Feature. In Communications in Computer
and Information Science. 1(3), 101-103
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
318
