Relevance and Mutual Information-based Feature Discretization
Artur J. Ferreira
1,3
and Mario A. T. Figueiredo
2,3
1
Instituto Superior de Engenharia de Lisboa, Lisboa, Portugal
2
Instituto Superior T´ecnico, Lisboa, Portugal
3
Instituto de Telecomunicac¸˜oes, Lisboa, Portugal
Keywords:
Classification, Feature Discretization, Mutual Information, Quantization, Supervised Learning.
Abstract:
In many learning problems, feature discretization (FD) techniques yield compact data representations, which
often lead to shorter training time and higher classification accuracy. In this paper, we propose two new FD
techniques. The first method is based on the classical Linde-Buzo-Gray quantization algorithm, guided by a
relevance criterion, and is able to work in unsupervised, supervised, or semi-supervised scenarios, depending
on the adopted measure of relevance. The second method is a supervised technique based on the maximization
of the mutual information between each discrete feature and the class label. For both methods, our experiments
on standard benchmark datasets show their ability to scale up to high-dimensional data, attaining in many cases
better accuracy than other FD approaches, while using fewer discretization intervals.
1 INTRODUCTION
A typical dataset is composed of categorical and/or
numeric features. The categorical features are dis-
crete by nature. The numeric features use real or
integer representations. In some cases, these fea-
tures have noisy values or show minor fluctuations
that are irrelevant or even harmful for the learning
task at hand. For such features, the performance of
machine learning and data mining algorithms can be
improved by discretization. Moreover, some learn-
ing algorithms require a discrete representation of
the data. In order to address these problems, the
use of feature discretization (FD) (Witten and Frank,
2005) techniques has been extensively considered in
the past. FD provides compact representations, with
lower memory usage, while at the same time it may
reduce the training time and improve the classifica-
tion accuracy. The literature on FD includes many
supervised and unsupervised techniques (i.e., making
use, or not, of class labels) (Witten and Frank, 2005;
Dougherty et al., 1995; Jin et al., 2009; Liu et al.,
2002; Kotsiantis and Kanellopoulos, 2006).
In this paper, we propose two new FD techniques.
The first one is based on the classical Linde-Buzo-
Gray (LBG) (Linde et al., 1980) quantization algo-
rithm, along with a relevance criterion that guides the
discretization process, being able to work in unsuper-
vised, supervised, or semi-supervised learning. The
second technique is supervised and is based on the
mutual information (MI) (Cover and Thomas, 1991)
between each (discretized) feature and the class label.
The remainder of this paper is organized as fol-
lows. Section 2 reviews the advantages and disad-
vantages of using FD techniques, describing some
unsupervised and supervised techniques. Section 3
presents our proposed methods for FD. The experi-
mental evaluation is carried out in Section 4 and the
paper ends in Section 5 with some concluding re-
marks and directions for future work.
2 FEATURE DISCRETIZATION
In this section, we provide some background on FD
techniques, reviewing their benefits and drawbacks.
Brief descriptions of unsupervised and supervised FD
techniques are provided in Subsection 2.1 and Sub-
section 2.2, respectively.
Regardless of the type of classifier considered, FD
techniques aim at finding a representation of each fea-
ture that contains enough information for the learning
task at hand, while ignoring minor fluctuations that
may be irrelevant for that task. The use of a discretiza-
tion technique will lead to a more compact (using less
memory), and hopefully to a better representation of
the data for learning purposes, as compared to the use
of the original features.
68
Ferreira A. and Figueiredo M. (2013).
Relevance and Mutual Information-based Feature Discretization.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 68-77
DOI: 10.5220/0004268000680077
Copyright
c
 SciTePress

A typical dataset with numeric features uses real
or integer representations. It has been found that the
use of FD techniques, with or without a coupled fea-
ture selection (FS) technique, may improve the results
of many learning methods (Dougherty et al., 1995;
Witten and Frank, 2005). Although supervised dis-
cretization may, in principle, lead to better classi-
fiers, it has been found that unsupervised FD meth-
ods perform well on different types of data (see for
instance (Yang and Webb, 2001)).
The quality of discretization is usually assessed by
two indicators: the generalization error and the com-
plexity, i.e., the number of intervals or equivalently
the number of bits used to represent each instance.
A possible drawback of FD is arguably the (time and
memory) cost of the discretization procedure.
A detailed description of many FD methods can
be found in (Dougherty et al., 1995; Jin et al., 2009;
Liu et al., 2002; Kotsiantis and Kanellopoulos, 2006)
and the many references therein.
2.1 Unsupervised Methods
The most common techniques for unsupervised FD
are (Witten and Frank, 2005): equal-interval binning
(EIB), which performs uniform quantization; equal-
frequency binning (EFB) (Chiu et al., 1991), which
obtains a non-uniform quantizer with intervals such
that, for each feature, the number of occurrences in
each interval is the same; proportional k-interval dis-
cretization (PkID) (Yang and Webb, 2001), which
computes the number and size of the discretization
intervals as functions of the number of training in-
stances.
EIB is obviously the simplest and easiest to imple-
ment, but is sensitive to outliers. In EFB, the quanti-
zation intervals are smaller in regions where there are
more occurrences of the values of each feature; EFB
is thus less sensitive to outliers, as compared to EIB.
In the EIB and EFB methods, the user can choose the
number of discretization bins. In contrast, the PkID
method sets the number and size of the discretization
intervals as a function of the number of training in-
stances, seeking a trade-off between bias and variance
of the class probability estimate of a na¨ıve Bayes clas-
sifier (Yang and Webb, 2001).
Recently, we have proposed an unsupervised
scalar FD method (Ferreira and Figueiredo, 2012)
based on the LBG algorithm (Linde et al., 1980). For
a given number of discretization intervals, LBG dis-
cretizes the data seeking the minimum mean square
error (MSE) with respect to the original representa-
tion. This approach, named unsupervised LBG (U-
LBG 1) and described as Algorithm 1, applies the
LBG algorithm to each feature independently and
stops when the MSE falls below a threshold ∆ or when
the maximum number of bits q per feature is reached.
A variant of U-LBG1, named U-LBG2, using a fixed
number of bits per feature q was also proposed. Both
U-LBG1 and U-LBG2 rely on the idea that a discrete
representation with low MSE is adequate for learning.
2.2 Supervised Methods
The information entropy minimization (IEM)
method (Fayyad and Irani, 1993), based on the
minimum description length (MDL) principle, is one
of the oldest and most often used methods for super-
vised FD. The key idea of using the MDL principle
is that the most informative features to discretize
are the most compressible ones. The IEM method
is based on the use of the entropy minimization
heuristic for discretization of a continuous value into
multiple intervals. IEM adopts a recursive approach
computing the discretization cut-points in such a
way that they minimize the amount of bits needed to
represent the data. It follows a top-down approach
in the sense that it starts with one interval and splits
intervals in the process of discretization.
The method termed IEM variant (IEMV)
(Kononenko, 1995) is also based on an entropy
minimization heuristic to choose the discretization
intervals. It applies a function, based on the MDL
principle, which decreases as the number of different
values for a feature increases.
The supervised static class-attribute interdepen-
dence maximization (CAIM) (Kurganand Cios, 2004)
algorithm aims to maximize the class-attribute in-
terdependence and to generate a (possibly) minimal
number of discrete intervals. The algorithm does not
Algorithm 1: U-LBG1.
Input: X, n× d matrix training set (n patterns, d features).
∆,q: maximum expected distortion and maximum
number of bits/feature.
Output:
e
X: n× d matrix, discrete feature training set.
Q
1
b
1
,..., Q
d
b
d
: set of d quantizers (one per feature).
1: for i = 1 to d do
2: for b = 1 to q do
3: Apply LBG to the i-th feature to obtain a b-bit
quantizer Q
b
(·);
4: Compute MSE
i
=
1
n
∑
n
j=1
(X
ij
− Q
b
(X
ij
))
2
;
5: if (MSE
i
≤ ∆ or b = q) then
6: Q
i
(·) = Q
b
(·); {/* Store the quantizer. */}
7:
e
X
i
= Q
i
(X
i
); {/* Quantize feature. */}
8: break; {/* Proceed to the next feature. */}
9: end if
10: end for
11: end for
RelevanceandMutualInformation-basedFeatureDiscretization
69

require a predefined number of intervals, as opposed
to some other FD methods. Experimental results re-
ported show that CAIM compares favorably with six
other FD discretization algorithms, in that the dis-
crete attributes generated by CAIM almost always
have the lowest number of intervals and the highest
class-attribute interdependency, achieving the highest
classification accuracy (Kurgan and Cios, 2004).
Finally, we mention class-attribute contingency
coefficient (CACC) (Tsai et al., 2008), which is an
incremental, supervised, top-down FD method, that
has been shown to achieve promising results regard-
ing execution time, number of discretization intervals,
and training time of the classifiers.
3 PROPOSED METHODS
3.1 Relevance-based LBG
As in U-LBG1 (Algorithm 1), our FD proposal,
named relevance-based LBG (R-LBG) and described
in Algorithm 2, uses the LBG algorithm, discretizing
data with a variable number of bits per feature. We
use a relevance function, denoted @rel, and a (non-
negative) stopping factor, ε. The relevance function,
producing non-negative values, is applied after each
discretization. R-LBG behaves differently, depend-
ing on the value of ε. If ε is positive, whenever there
is an increase below ε on the relevance between two
subsequent discrete versions (with b and b + 1 bits),
discretization is halted and b bits are kept, for that
feature; otherwise, with a significant (larger than ε)
increase on the relevance, it discretizes with one more
bit, assessing the new relevance. In summary, it dis-
cretizes a feature with an increasing number of bits,
stopping only when there is no significant increase
on the relevance of the recently discretized feature.
If ε = 0, each feature is discretized from 1 up to the
maximum q bits and the corresponding relevance is
assessed on each discretization. Then, the minimum
number of bits that ensures the highest relevance is
kept and applied to discretize that feature. Regardless
of the value of ε, the method discretizes data with a
variable number of bits per feature.
The relevance assessment r
ib
= @rel(Q
i
b
(X
i
);...),
of feature i with b bits, in line 5 of Algorithm 2, can
refer to unsupervised, supervised, or semi-supervised
learning. This depends on how the relevance function
makes use (or not) of the class labels. The value of ε,
when different from zero, should be set according to
the range of the @rel function.
There are many different choices for the rele-
vance criteria of R-LBG. In the unsupervised case, if
we consider @rel = MSE (between original and dis-
crete features) we have the unsupervised U-LBG1 ap-
proach. Another relevance criterion is given by the
quotient between the variance of the discrete feature
and the number of discretization intervals
NVAR(
e
X
i
) = var(
e
X
i
) / 2
b
i
, (1)
where b
i
is the number of bits of the discrete feature.
For the supervised case, we propose to compute
relevance by the mutual information (MI) (Cover and
Thomas, 1991) between discretized features
e
X
i
, with
b
i
bits and the class label vector y
MI(
e
X
i
;y) = H(
e
X
i
) − H(
e
X
i
|y)
= H(y) − H(y|
e
X
i
). (2)
where H(.) and H(.|.) denote entropy and conditional
entropy, respectively (Cover and Thomas, 1991).
There are many other (unsupervised and super-
vised) feature relevance criteria; in fact, all the criteria
used in feature selection methods to rank features are
Algorithm 2: R-LBG - Relevance-based LBG.
Input: X: n× d matrix training set (n patterns, d features).
y: n-length vector with class labels (supervised).
q: maximum number of bits per feature.
@rel,ε (≥ 0): relevance function, stopping factor.
Output:
e
X: n× d matrix, discrete feature training set.
Q
1
b
1
,..., Q
d
b
d
: set of d quantizers (one per feature).
1: for i = 1 to d do
2: pRel = 0; {/* Initial/previous rel. for feature i. */}
3: for b = 1 to q do
4: Apply LBG to the i-th feature to obtain a b-bit
quantizer Q
i
b
(·);
5: Compute r
ib
= @rel(Q
i
b
(X
i
);...), relevance of
feature i with b bits;
6: if (ε == 0) then
7: continue; {/* Discretize up to q bits. */}
8: end if
9: if ( (r
ib
− pRel) > ε) then
10: Q
i
(·) = Q
b
(·);
e
X
i
= Q
i
b
(X
i
); {/* High
increase. Store quantizer and discretize. */}
11: else
12: break; {/* Non-significant increase. Break
loop. Move on to the next feature. */}
13: end if
14: pRel = r
ib
; {/* Keep previous relevance. */}
15: end for
16: end for
17: if (ε == 0) then
18: for i = 1 to d do
19: Get b
i
= arg max
b∈{1,...,q}
r
i∗
{/* Max. relevance. */}
20: Q
i
(·) ← Apply LBG (b
i
bits) to the i-th feature;
21:
e
X
i
= Q
i
b
i
(X
i
); {/* Discretize feature. */}
22: end for
23: end if
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
70

1 2 3 4 5 6 7 8 9 10
0
0.2
0.4
0.6
0.8
q bits/feature
MI
MI evolution on R−LBG (MI)
Feat. 1
Feat. 12
Feat. 16
Feat. 18
2 4 6 8 10 12 14 16 18
0
0.2
0.4
0.6
0.8
Feature
MI with q=1 and q=10 bits
q=1
q=10
Figure 1: R-LBG (MI) discretization on the Hepatitis
dataset. Top: MI as a function of the number of bits
q ∈ {1, ... ,10}, for features 1, 12, 16, and 18. Bottom: MI
with q = 1 and q = 10 bits, for all the d = 19 features.
potential candidates to serve as a relevance measure
in R-LBG. The relevance function can also be cho-
sen such that it only uses the class label for those in-
stances for which it is available, thus being usable in
semi-supervised learning.
As an illustration of the supervised case, Figure 1
(top) shows the evolution of the MI between the class
label and some of the features discretized by the R-
LBG algorithm, using q ∈ {1,...,10} bits per feature,
for the Hepatitis dataset. In the bottom plot, we com-
pare the MI values obtained by discretizing with q= 1
and q = 10 bits, for each of the 19 features of the same
dataset. The top plot shows that for features 1, 16,
and 18, the MI grows with the number of bits and
then it levels off. For feature 12 (which is categori-
cal, thus originally discrete), as obviously expected,
an increasing number of bits does not lead to a higher
MI. Thus, our method handles both continuous and
categorical features and the relevance values provide
a feature ranking score. In practice, the choice of ad-
equate values of ε, which depends on the type of data,
can be done using these plots, by checking how the
MI increases. In the bottom plot, we see that some
features, such as 3, 4, 5, and 6, show no significant
MI increase, when moving from q = 1 to q = 10. On
the other hand, for features 14 to 18, we have a strong
MI increase, which usually corresponds to numeric
informative features.
3.2 Mutual Information Discretization
In this subsection we present the proposed supervised
FD method, named mutual information discretization
(MID). Essentially, the MID method consists in dis-
cretizing each feature individually,computing the dis-
cretization cut-points in order to maximize the MI of
the discrete feature with the class label. The key mo-
tivation for this FD proposal is that the MI between
features and class labels has been extensively used as
a FS criterion; see the seminal work in (Battiti, 1994)
and (Brown et al., 2012) for a review of MI-based FS
methods. It is thus expectable that a good criterion for
FS will also be adequate for FD.
The usual argument is based on bounds for the
probability of error which depend on the MI be-
tween the observations and the class label, namely
the Fano, Hellman-Raviv, and Santhi-Vardi bounds
(Brown et al., 2012), (Santhi and Vardy, 2006). The
Hellman-Raviv bound (Hellman, 1970) on the Bayes
risk is given by
err
Bayes
(
e
X
i
) ≤
1
2
H(
e
X
i
|y) (3)
while the Santhi-Vardy bound (Santhi and Vardy,
2006) is
err
Bayes
(
e
X
i
) ≤ 1− 2
−H(
e
X
i
|y)
. (4)
In order to maximize the MI (2), one must min-
imize H(
e
X
i
|y), that is, the uncertainty about the fea-
ture value, given a known class label. We have 0 ≤
H(
e
X
i
|y) ≤ H(
e
X
i
), with H(
e
X
i
|y) = 0 meaning deter-
ministic dependence (an ideal feature) and H(
e
X
i
|y) =
H(
e
X
i
) corresponding to independence between the
feature and the class label (a useless feature). On
the other hand, H(y) does not change with discretiza-
tion; thus, maximizing (2) is equivalent to minimiz-
ing H(y|
e
X
i
), that is, the uncertainty about the class
label given the feature. We have 0 ≤ H(y|
e
X
i
) ≤ H(y),
with H(y|
e
X
i
) = 0 corresponding to deterministic de-
pendence (again, the ideal case) and H(y|
e
X
i
) = H(y)
meaning independence (a useless feature). For an
ideal feature (one that is a deterministic injective
function of the class label), we have
MI(
e
X
i
;y) = H(
e
X
i
) = H(y). (5)
Of course, the maximum possible value for MI(
e
X
i
;y)
depends on both the number of bits used to discretize
X
i
and the number of classes c. If we discretize X
i
with b
i
bits, its maximum entropy is H
max
(
e
X
i
) = b
i
bit/symbol; the maximum value of the class entropy
is H
max
(y) = log
2
(c) bit/symbol, which corresponds
to c equiprobable classes. We thus conclude that the
maximum value of the MI between the class label and
a discretized feature (with b
i
bits) is
MI
max
(
e
X
i
;y) = min{b
i
, log
2
(c)}. (6)
RelevanceandMutualInformation-basedFeatureDiscretization
71

Figure 2: Illustration of the progressive and recursive par-
tition algorithm for feature discretization, using q = 3 bits,
leading to a 8-interval quantizer.
In the binary case c = 2, we have MI
max
(
e
X
i
;y) = 1
bit. Moreover, to attain the maximum possible value
for the MI, one must choose the maximum number
of bits q taking into account this expression; this im-
plies that q ≥ ⌈log
2
(c)⌉, which is more meaningful
for multi-class problems.
3.2.1 Algorithm Outline
At the discretization stage, we search for discretiza-
tion boundaries such that the resulting discrete fea-
ture has the highest MI with the class label. Thus,
as described above, by maximizing the MI at each
partition and each cut-point we are aiming at lever-
aging the performance of the discrete feature, leading
to higher accuracy. The method works in a recursive
way, by successively breaking each feature into inter-
vals, as depicted in Figure 2 with q = 3 bits yielding
a 8-interval non-uniform quantizer.
We propose two versions of the MID technique.
The first, named MID fixed, uses a fixed number of q
bits per feature. In summary, given a training set with
n instances and d features, X and a maximum number
of bits per feature q, the MID fixed method applies the
recursive discretization method just described, using
up to q bits per feature, yielding quantizer Q
i
(·) for
feature i and the discretized feature
e
X
i
= Q
i
(X
i
).
The second version, named MID variable allo-
cates up to q bits per feature, leading to a variable
number of bits per feature. As in R-LBG, we halt the
bit allocation for feature X
i
with b bits, whenever its
discretization with b+ 1 bits does not lead to a signif-
icant increase (larger than ε) on the MI(
e
X
i
;y). As a
consequence, the MID variable version will produce
1 2 3 4 5 6 7 8
0
0.5
1
1.5
#Bits (q)
MI
MI for features 1, 7, and 8 on the Wine dataset
Feat. 1
Feat. 7
Feat. 8
1 2 3 4 5 6 7 8 9 10 11 12 13
0
0.5
1
1.5
Feature
MI
MI with q ∈ {1,2,3,4} bits on the Wine dataset
q=1
q=2
q=3
q=4
Figure 3: MID for the Wine dataset (d = 13 features, c = 3
classes). Top: evolution of MI for features 1, 7, and 8, with
q ∈ {1,. .. ,8}. Bottom: MI between discretized features
and the class label, for q ∈ {1,2,3,4}.
fewer discretization intervals (and thus fewer bits per
instance), as compared to the MID fixed method. By
setting ε = 0, MID variable discretizes feature
e
X
i
, with
maximum MI, using the smallest possible number of
bits b
i
≤ q (it acts in a similar fashion as R-LBG).
The number of discretization intervals depends on the
value of ε; larger values will lead to fewer intervals.
Figure 3 (top) plots the evolution of MI for fea-
tures 1, 7, and 8 for the Wine dataset. We see an
increase in the first few bits and then the values of
MI level off. The average MI values for all d = 13
features are 0.4977, 0.6810, 0.8294, and 0.8294, for
q ∈ {1,2,3,4} bits, respectively. The training par-
tition has class entropy H
max
(y) = log
2
(3) = 1.585
bits. In the bottom plot, we see an overall increase
of the MI when moving from 1 to 3 bits; however, us-
ing q = 4, there is no appreciable increase on the MI.
4 EXPERIMENTAL EVALUATION
This section reports experimental results of our FD
techniques on several public domain datasets, for the
task of supervised classification. We use a 10-fold
cross validation (CV) strategy. In each fold, the quan-
tizers are learned in the training partition and then ap-
plied to the test partition. We apply linear support
vector machines (SVM), na
¨
ıve Bayes (NB), and K-
nearest-neighbors (KNN) (with K = 3) classifiers, of
the PRTools
1
toolbox (Duin et al., 2007).
Table 1 briefly describes the publicly available
datasets that were used in our experiments. We chose
1
www.prtools.org/prtools.html
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
72

Table 1: Datasets, with c classes, n instances, and listed by
order of increasing dimensionality d.
Dataset d c n Type of Data
Wine 13 3 178 Wine cultivar
Hepatitis 19 2 155 Biological
Ionosphere 34 2 351 Radar return
Colon 2000 2 62 Microarray
SRBCT 2309 4 83 Microarray
AR10P 2400 10 130 Face database
PIE10P 2420 10 210 Face database
Leukemia1 5327 3 72 Microarray
TOX-171 5748 4 171 Microarray
Brain-Tumor1 5920 5 90 Microarray
ORL10P 10304 10 100 Face database
Prostate-Tumor 10509 2 102 Microarray
Leukemia2 11225 3 72 Microarray
GLI-85 22283 2 85 Microarray
several well-known datasets with different kinds of
data, problems, classes, and dimensionality, includ-
ing datasets from the UCI repository
2
(Frank and
Asuncion, 2010), face database, and bioinformat-
ics datasets from the gene expression model selector
(GEMS) project
3
(Statnikov et al., 2005), and from
the Arizona state university (ASU)
4
repository (Zhao
et al., 2010).
The experimental results are organized as follows.
We start, in Subsection 4.1, by evaluatingthe behavior
of our supervised FD methods using a variable num-
ber of bits per feature. In Subsection 4.2, we com-
pare our methods with existing unsupervised and su-
pervised FD techniques (reviewed in Subsections 2.1
and 2.2, respectively). This evaluation is focused both
on the complexity and the generalization error. Sub-
section 4.3 provides some discussion on these results.
4.1 Analysis of Our Approaches
For both the R-LBG and MID variable algorithms,
we use different values of ε and assess the number
of discretization intervals and the generalization er-
ror. Table 2 reports experimental results with the av-
erage number of bits per instance (with q = 4 and
ε ∈ {0,0.1}) and the test set error rate for the linear
SVM classifier (No FD denotes the use of the original
features).
On the R-LBG algorithm, ε = 0 usually leads to a
larger number of bits per instance, as compared with
ε = 0.1. This happens because with ε = 0 we are
aiming at finding the maximum relevance, whereas
with ε > 0 we halt the discretization process at earlier
stages. For the MID variable algorithm, ε = 0 leads
2
archive.ics.uci.edu/ml/datasets.html
3
www.gems-system.org
4
featureselection.asu.edu/datasets.php
Table 2: Evaluation of R-LBG (@rel = MI) and MID vari-
able with q = 4. For each dataset, the first row displays
the total number of bits per instance and the second row the
test set error rate (%), of a 10-fold CV for the linear SVM
classifier. The best error rate is in bold face.
R-LBG (MI) MID variable
D. / No FD ε = 0 ε = 0.1 ε = 0 ε = 0.1
Wine 52.0 30.6 38.3 26.2
3.9 2.8 1.7 3.4 2.8
Hepatitis 46.5 68.8 28.5 65.6
21.3 15.5 21.9 18.7 18.1
Ionosphere 129.0 102.4 73.0 85.0
12.8 14.0 12.5 9.4 5.7
Colon 7954.6 7564.0 4682.0 6151.9
17.7 19.4 14.5 19.4 14.5
SRBCT 9222.5 8827.7 7144.2 7180.3
0.0 0.0 0.0 0.0 0.0
AR10P 9599.8 9583.2 8620.4 8640.4
0.8 0.8 0.8 0.0 0.0
PIE10P 9679.9 9662.5 8550.7 8543.4
0.0 0.0 0.0 0.0 0.0
Leukemia1 21248.2 19818.7 14636.9 15555.9
8.3 4.2 5.6 8.3 6.9
TOX-171 22988.5 21439.2 19012.4 20070.8
14.6 2.3 2.9 4.1 4.1
B-Tumor1 23649.6 22174.4 17531.0 17436.5
11.1 8.9 10.0 10.0 10.0
ORL10P 41215.6 41195.1 37410.3 37410.2
1.0 1.0 1.0 2.0 2.0
P-Tumor 41735.0 40431.3 25493.1 36598.8
10.8 7.8 7.8 7.8 7.8
Leukemia2 44300.1 40072.9 31124.0 30255.4
5.6 1.4 1.4 1.4 1.4
GLI-85 88561.7 84364.2 54906.9 72131.8
10.6 8.2 8.2 8.2 8.2
to the choice of the minimum bits per feature that en-
sure the maximum MI; for this reason, with ε = 0 we
usually have fewer bits per instance as compared with
ε > 0. Regarding the classification accuracy, ε = 0
usually attains the best results with a few exceptions.
We have assessed the statistical significance of our
results with the Friedman test (Friedman, 1940), to
the average test set error rates, as suggested by (Dem-
sar, 2006) and (Garcia and Herrera, 2008). For this
purpose, we have used the JAVA tool of (Garcia and
Herrera, 2008)
5
. For the results in Table 2, the Fried-
man test reported a p-value of 0.04164 < 0.05, stating
that these results are statistically significant.
In order to assess how discretization is affected
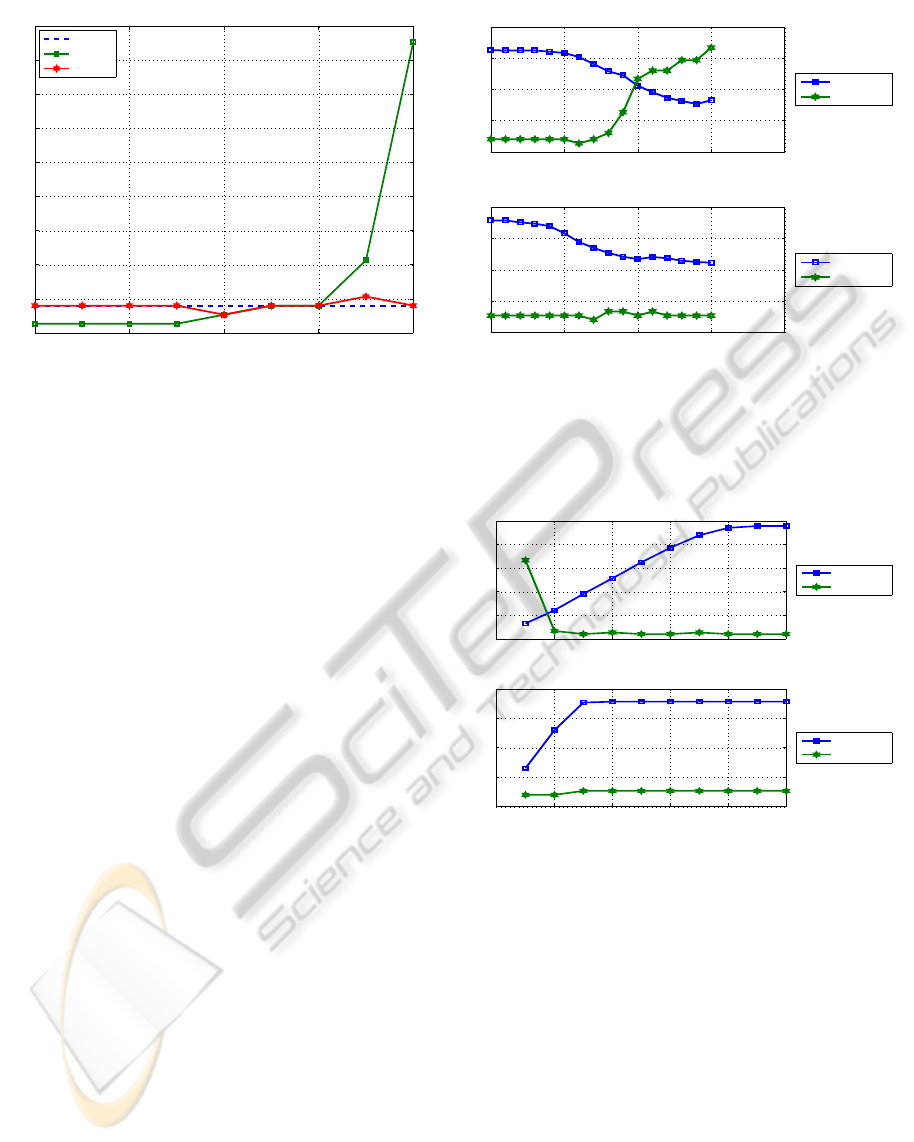
by the values of ε, Figure 4 shows the test set error
rate for a 10-fold CV of the NB classifier on data dis-
cretized by R-LBG and MID variable with q = 5 bits
and ε ranging in the real interval from 0 to 0.2, on the
Wine dataset. For the small values of ε, the R-LBG
algorithm leads to discrete features with lower test set
error rate than those obtained by the MID variable
algorithm. On both algorithms, by choosing values
5
sci2s.ugr.es/keel/multipleTest.zip
RelevanceandMutualInformation-basedFeatureDiscretization
73

0 0.05 0.1 0.15 0.2
0
5
10
15
20
25
30
35
40
45
ε
Err [%]
Test Set Error Rate on the Wine dataset
No FD
R−LBG
MID var
Figure 4: R-LBG (MI) and MID variable discretization on
the Wine dataset with q = 5 bits. Test set error rate (%)
of the NB classifier for a 10-fold CV, as function of the ε
parameter, ranging in the real interval from 0 to 0.2.
of ε from zero roughly up to 0.15, we get a gener-
alization error equal or better than the baseline error
(without FD). On the R-LBG algorithm, with ε close
to 0.2, the number of discretization intervals per fea-
ture drops yielding poor discretizations and the test
error rate degrades seriously. The MID algorithm is
less sensitive to the increase of the ε parameter; in
the MID variable approach, we have a wide range of
values of ε that lead to low generalization error.
Figure 5 shows the evolution of both the number
of bits/instance and the test set error rate for a 10-
fold CV of the NB classifier on data discretized by
R-LBG and MID variable with q = 5 bits and ε in the
real interval from 0 to 0.3, on the Wine dataset. As
ε increases, the number of discretization intervals and
thus the number of bits per instance decreases. The
test set error rate only becomes higher at larger val-
ues of ε. Again, the R-LBG algorithm shows higher
sensitivity with respect to the increase of this parame-
ter, since the test set error rate becomes unacceptably
high for ε close to 0.15. On the other hand, the MID
variable algorithm exhibits a more stable behavior as
compared to R-LBG; the corresponding test set error
rate does not increase so fast as in R-LBG, whenever
the number of bits per instance decreases.
Figure 6 shows the effect of varying the maximum
number of bits for discretization, q ∈ {1, .. ., 10}, for
both R-LBG and MID variable, keeping a fixed value
ε = 0.05 (again with both the NB classifier and the
Wine dataset). By increasing the maximum number
of bits per feature, MID variable uses fewer bits per
instance as compared to the R-LBG algorithm. The
classification accuracies are similar and they both ex-
hibit a stable behavior in the sense that an (excessive)
0 0.1 0.2 0.3 0.4
0
20
40
60
80
ε
R−LBG: Bits/Instance and Error on the Wine dataset
Bits/Inst.
Error [%]
0 0.1 0.2 0.3 0.4
0
10
20
30
40
ε
MID var: Bits/Instance and Error on the Wine dataset
Bits/Inst.
Error [%]
Figure 5: Number of bits/instance and the test set error rate
(%) for a 10-fold CV of the NB classifier on data discretized
by R-LBG and MID variable with q = 5 bits and ε in the real
interval from 0 to 0.3, on the Wine dataset for R-LBG (top)
and MID variable (bottom).
0 2 4 6 8 10
0
20
40
60
80
100
#Bits (q)
R−LBG: Bits/Instance and Error on the Wine dataset
Bits/Inst.
Error [%]
0 2 4 6 8 10
0
10
20
30
40
#Bits (q)
MID var: Bits/Instance and Error on the Wine dataset
Bits/Inst.
Error [%]
Figure 6: Number of bits/instance and the test set error
rate (%) for a 10-fold CV of the NB classifier on data dis-
cretized by R-LBG and MID variable with ε = 0.05, and
q ∈ {1,.. .,10} bits, on the Wine dataset.
increase on the maximum number of bits per feature
q does not degrade the test set error rate.
4.2 Comparison with Existing Methods
4.2.1 Unsupervised Discretization
First, we assess the behavior of R-LBG in unsuper-
vised mode, comparing it with five existing unsuper-
vised FD methods (see Subsection 2.1). We evaluate
the average number of discretization intervals and the
average 10-fold CV error (%), attained by each FD
method, with q = 3 bits. R-LBG uses @rel = NVAR
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
74

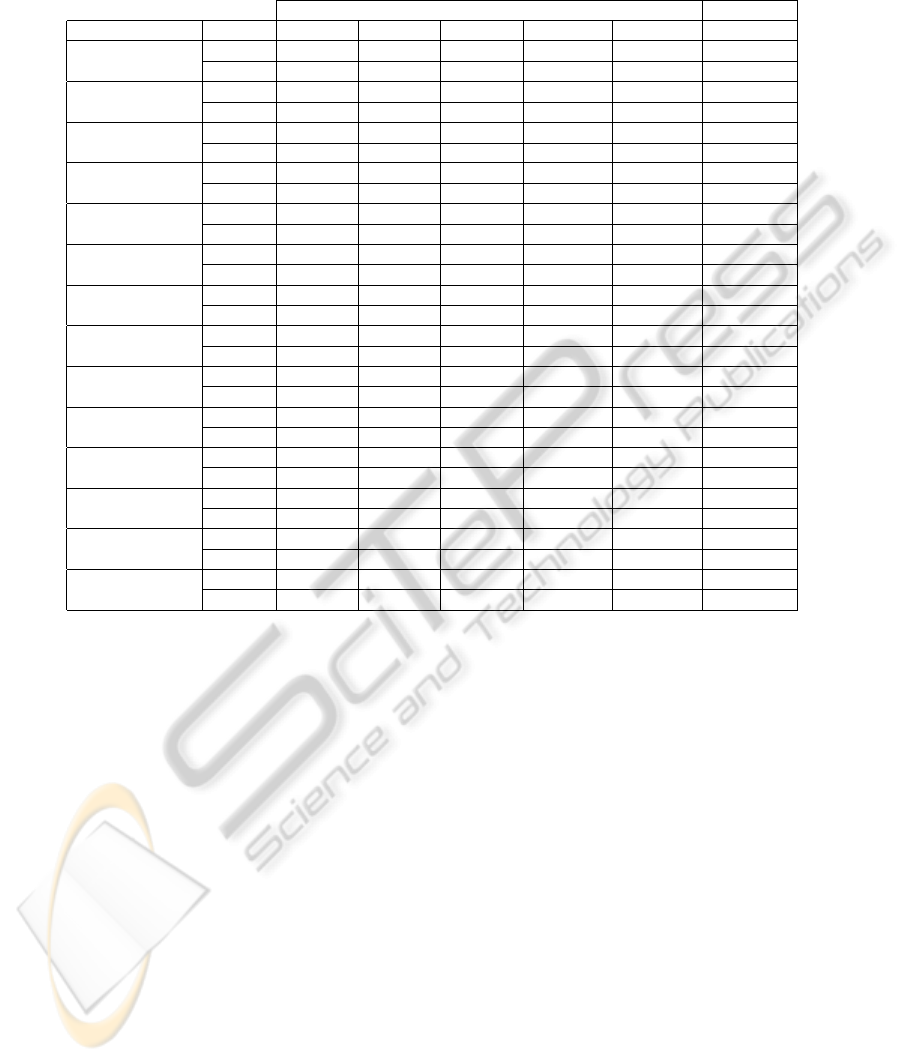
Table 3: Evaluation of unsupervised FD. For each dataset, the first row presents the average total number of bits per instance
and the second row has the average test set error rate (%), using a 10-fold CV for the linear SVM classifier. The best error rate
is in bold face. We have used q = 3 bit/feature, ∆ = 0.05range(X
i
) for U-LBG1, @rel = NVAR, and ε = 0.25, for R-LBG.
Existing Methods Proposed
Dataset No FD EIB EFB PkID U-LBG1 U-LBG2 R-LBG
Wine 39.0 39.0 52.0 22.0 39.0 14.8
4.5 3.4 4.5 3.9 3.9 3.4 7.9
Hepatitis 57.0 57.0 46.0 28.9 57.0 38.6
22.6 20.0 20.6 21.9 20.0 19.4 18.7
Ionosphere 99.0 99.0 145.0 44.9 99.0 75.4
12.8 11.1 13.1 16.2 10.8 14.0 11.4
Colon 6000.0 6000.0 6000.0 6000.0 6000.0 2534.4
19.4 16.1 11.3 12.9 14.5 14.5 11.3
SRBCT 6924.0 6924.0 6924.0 2825.3 6924.0 2641.2
0.0 0.0 0.0 0.0 0.0 0.0 1.2
AR10P 7200.0 7200.0 9267.8 7200.0 7200.0 6568.6
0.8 0.0 0.8 0.8 0.8 0.8 1.5
PIE10P 7260.0 7260.0 9680.0 7260.0 7260.0 3774.4
0.0 0.0 0.0 0.0 0.0 0.0 0.0
Leukemia1 15981.0 15981.0 15981.0 15981.0 15981.0 5733.0
5.6 2.8 4.2 4.2 4.2 4.2 2.8
TOX-171 17244.0 17244.0 22992.0 17244.0 17244.0 5847.6
9.9 1.2 1.8 1.2 1.8 1.8 8.2
Brain-Tumor1 17760.0 17760.0 23680.0 17760.0 17760.0 6085.4
13.3 8.9 11.1 11.1 8.9 8.9 11.1
ORL10P 30912.0 30912.0 41216.0 30912.0 30912.0 19385.4
1.0 1.0 1.0 1.0 1.0 1.0 1.0
Prostate-Tumor 31527.0 31527.0 42035.4 31520.0 31527.0 11394.0
10.8 8.8 8.8 8.8 8.8 8.8 8.8
Leukemia2 33675.0 33675.0 33675.0 33675.0 33675.0 12431.4
4.2 2.8 2.8 2.8 2.8 2.8 4.2
GLI-85 66849.0 66849.0 66849.0 66849.0 66849.0 25118.7
14.1 10.6 8.2 8.2 9.4 9.4 8.2
and ε = 0.25. Table 3 shows these values for the linear
SVM classifier.
For all datasets, the use of a FD technique leads to
equal or better results as compared to the use of the
original features. R-LBG leads to the best test set er-
ror rate in 7 out of 14 tests. Moreover, in the majority
of these tests, R-LBG computes fewer discretization
intervals, as compared to the other techniques. This
difference on the discretization intervals is most no-
ticed in the higher-dimensional datasets.
For the test set error rates in Table 3, the Friedman
test has reported a p-value of 0.04287 < 0.05, stating
that these results have statistical significance.
4.2.2 Supervised Discretization
We now assess the behavior of our methods for super-
vised FD. The MID fixed, MID variable, and R-LBG
methods, with q = 3 bits, are compared against the
four supervised FD techniques described in Subsec-
tion 2.2. R-LBG uses MI as the relevance measure.
For both R-LBG and MID variable we use ε = 0.1.
Table 4 reports linear SVM results for a 10-fold CV
and the average number of bits per instance.
Again, the use of a FD technique improves on the
test set error rate, as compared to the use of the orig-
inal features, for the 14 datasets considered in this
experimental evaluation. The CAIM and CACC al-
gorithms are not suitable for the higher-dimensional
datasets, since they both take a prohibitive running
time (hours) as compared to other approaches. One
of our approaches usually attains the best result, ex-
cept in three cases (two in which IEMV is the best and
one where CAIM attains the best result). Within our
approaches, the R-LBG and MID variable methods
attain the best results, which suggests:
i) the adequacy of MI between features and class la-
bels for discretization purposes;
ii) a variable number of bits per feature is preferable
to the use of a fixed number, regarding both com-
plexity and generalization error.
The p-value of the Friedman test for the error
rates of Table 4 (excluding both CAIM and CACC)
is 0.00461 < 0.05, showing statistical significance.
RelevanceandMutualInformation-basedFeatureDiscretization
75

Table 4: Evaluation of supervised FD. For each dataset, the first row presents the average total number of bits per instance and
the second row has the average test set error rate (%), using a 10-fold CV for the linear SVM classifier. The best error rate is
in bold face. We have used q = 3 bit/feature, @rel = MI, and ε = 0.1 for both R-LBG and MID variable.
Existing Methods Proposed Methods
Dataset No FD IEM IEMV CAIM CACC R-LBG MID fixed MID variable
Wine 19.8 21.3 39.0 39.0 27.4 39.0 23.0
5.1 2.2 1.7 2.8 2.8 3.9 2.8 1.7
Hepatitis 45.5 42.9 34.6 43.3 52.3 57.0 50.0
19.4 22.6 21.3 17.4 20.0 21.9 16.8 19.4
Ionosphere 84.4 83.0 65.0 96.9 85.0 99.0 73.3
12.5 11.7 9.4 10.5 12.5 10.8 7.7 6.0
Colon 11341.3 11089.3 4000.0 7431.2 5765.4 6000.0 5121.5
17.7 16.1 16.1 16.1 16.1 17.7 19.4 16.1
SRBCT 12476.1 9691.4 6924.0 6924.0 6248.1 6924.0 6553.5
0.0 0.0 0.0 1.2 0.0 0.0 0.0 0.0
AR10P 12903.6 7138.4 7200.0 7200.0 7145.6 7200.0 7266.3
0.8 2.3 20.0 0.8 0.0 0.0 0.0 0.0
PIE10P 9103.4 5264.0 7260.0 7260.0 7077.3 7260.0 7154.7
0.0 0.0 1.9 0.0 0.0 0.0 0.0 0.0
Leukemia1 28435.3 26034.7 * * 14656.1 15981.0 14278.0
5.6 40.3 56.9 * * 4.2 2.8 2.8
TOX-171 36134.8 28253.7 * * 15725.6 17244.0 15824.2
15.2 5.8 2.9 * * 2.9 3.5 4.7
Brain-Tumor1 32808.3 27133.5 * * 15674.3 17760.0 16343.6
14.4 20.0 35.6 * * 11.1 10.0 8.9
ORL10P 26475.7 24176.8 * * 30863.0 30912.0 30786.9
2.0 9.0 1.0 * * 2.0 2.0 2.0
Prostate-Tumor 54395.6 51964.7 * * 30695.0 31527.0 28506.3
8.8 12.7 11.8 * * 5.9 6.9 7.8
Leukemia2 48380.1 40447.3 * * 28857.3 33675.0 28670.8
5.6 8.3 6.9 * * 2.8 2.8 2.8
GLI-85 135866.9 130689.1 * * 64065.0 66849.0 58633.4
10.6 11.8 12.9 * * 9.4 9.4 10.6
4.3 Summary and Discussion
In the comparison with state-of-the-art techniques for
unsupervised and supervised FD, our methods im-
prove on the test set error rate, in the majority of the
tests. Our proposals scale well for high-dimensional
data, contrary to other approaches. The adequacy of
MI between features and class labels for discretization
has been shown. Discretizing with a variable num-
ber of bits per feature is preferable in terms of both
complexity and generalization error, as compared to a
fixed number of bits, since it allows to attain the best
trade-off between the number of discretization inter-
vals and the generalization error. Our methods show
stability regarding the variation of their input parame-
ters q and ε. An excessive value on q does not lead to
an excessive number of discretization intervals, since
both R-LBG and MID variable stop allocating bits,
whenever the relevance criterion is not fulfilled. The
choice of ε is set by the maximum possible value of
the MI between the feature and the class label; setting
ε from 0 to 10% of the maximum MI seems adequate
for different kinds of data.
5 CONCLUSIONS
In many machine learning and data mining tasks, FD
is a useful pre-processing step. Even in cases where
FD is not required, it may be used to attain compact
and adequate representations of the data. Often, the
use of FD techniques improves on the generalization
error and lowers the training time.
In this paper, we have proposed two FD tech-
niques. The first one is based on the unsupervised
Linde-Buzo-Gray algorithm with a relevance crite-
rion to monitor the discretization process. Depend-
ing on the relevance criterion, this technique works
in unsupervised, supervised, or semi-supervised prob-
lems. The second technique is supervised and is based
on mutual information maximization between the dis-
crete feature and the class label. It uses a recursiveap-
proach that finds the optimal cut points in the mutual
information sense, being able to work with a fixed or
a variable number of bits per feature.
The experimental evaluation of these techniques
was carried out on publicly available binary and
multi-class, medium and high-dimensional datasets,
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
76

with different types of data. Under a supervised
learning evaluationtask with different classifiers, both
techniques have shown improvement as compared to
unsupervised and supervised FD approaches. The
first technique has obtained similar or better results,
when compared to its unsupervised counterparts. For
the supervised FD tests, the second technique has
proved to be more effective regarding the number of
discretization intervals and the generalization error.
For both techniques, the classifiers learned on dis-
crete features usually attain better accuracy than those
learned on the original ones. Both techniques scale
well for high-dimensional and multi-class problems.
As future work, we will explore the embedding of
feature selection in the discretization process.
REFERENCES
Battiti, R. (1994). Using mutual information for select-
ing features in supervised neural net learning. IEEE
Transactions on Neural Networks, 5:537–550.
Brown, G., Pocock, A., Zhao, M., and Luj´an, M. (2012).
Conditional likelihood maximisation: A unifying
framework for information theoretic feature selection.
J. Machine Learning Research, 13:27–66.
Chiu, D., Wong, A., and Cheung, B. (1991). Information
discovery through hierarchical maximum entropy dis-
cretization and synthesis. In Proc. of the Knowledge
Discovery in Databases, pages 125–140.
Cover, T. and Thomas, J. (1991). Elements of Information
Theory. John Wiley & Sons.
Demsar, J. (2006). Statistical comparisons of classifiers
over multiple data sets. Journal of Machine Learning
Research, 7:1–30.
Dougherty, J., Kohavi, R., and Sahami, M. (1995). Su-
pervised and unsupervised discretization of continu-
ous features. In Int. Conf. Mac. Learn. (ICML), pages
194–202.
Duin, R., Juszczak, P., Paclik, P., Pekalska, E., Ridder, D.,
Tax, D., and Verzakov, S. (2007). PRTools4.1: A Mat-
lab Toolbox for Pattern Recognition. Technical report,
Delft Univ. Technology.
Fayyad, U. and Irani, K. (1993). Multi-interval discretiza-
tion of continuous-valued attributes for classification
learning. In Proc. Int. Joint Conf. on Art. Intell. (IJ-
CAI), pages 1022–1027.
Ferreira, A. and Figueiredo, M. (2012). An unsupervised
approach to feature discretization and selection. Pat-
tern Recognition, 45:3048–3060.
Frank, A. and Asuncion, A. (2010). UCI machine learning
repository, available at http://archive.ics.uci.edu/ml.
Friedman, M. (1940). A comparison of alternative tests of
significance for the problem of m rankings. The An-
nals of Mathematical Statistics, 11(1):86–92.
Garcia, S. and Herrera, F. (2008). An extension on ”sta-
tistical comparisons of classifiers over multiple data
sets” for all pairwise comparisons. Journal of Ma-
chine Learning Research, 9:2677–2694.
Hellman, M. (1970). Probability of error, equivocation, and
the Chernoff bound. IEEE Transactions on Informa-
tion Theory, 16(4):368–372.
Jin, R., Breitbart, Y., and Muoh, C. (2009). Data discretiza-
tion unification. Know. Inf. Systems, 19(1):1–29.
Kononenko, I. (1995). On biases in estimating multi-valued
attributes. In Proc. Int. Joint Conf. on Art. Intell. (IJ-
CAI), pages 1034–1040.
Kotsiantis, S. and Kanellopoulos, D. (2006). Discretization
techniques: A recent survey. GESTS Int. Trans. on
Computer Science and Engineering, 32(1).
Kurgan, L. and Cios, K. (2004). CAIM discretization algo-
rithm. IEEE Trans. on Know. and Data Engineering,
16(2):145–153.
Linde, Y., Buzo, A., and Gray, R. (1980). An algorithm for
vector quantizer design. IEEE Trans. on Communica-
tions, 28:84–94.
Liu, H., Hussain, F., Tan, C., and Dash, M. (2002). Dis-
cretization: An Enabling Technique. Data Mining and
Knowledge Discovery, 6(4):393–423.
Santhi, N. and Vardy, A. (2006). On an improvement over
R´enyi’s equivocation bound. In 44-th Annual Allerton
Conference on Communication, Control, and Com-
puting.
Statnikov, A., Tsamardinos, I., Dosbayev, Y., and Aliferis,
C. F. (2005). GEMS: a system for automated cancer
diagnosis and biomarker discovery from microarray
gene expression data. Int J Med Inf., 74(7-8):491–503.
Tsai, C.-J., Lee, C.-I., and Yang, W.-P. (2008). A dis-
cretization algorithm based on class-attribute contin-
gency coefficient. Inf. Sci., 178:714–731.
Witten, I. and Frank, E. (2005). Data Mining: Practical
Machine Learning Tools and Techniques. Elsevier,
Morgan Kauffmann.
Yang, Y. and Webb, G. (2001). Proportional k-interval dis-
cretization for na¨ıve-Bayes classifiers. In 12th Eur.
Conf. on Machine Learning, (ECML), pages 564–575.
Zhao, Z., Morstatter, F., Sharma, S., Alelyani, S., Anand,
A., and Liu, H. (2010). Advancing feature selection
research - ASU feature selection repository. Technical
report, Arizona State University.
RelevanceandMutualInformation-basedFeatureDiscretization
77