Multiclass Diffuse Interface Models for

Semi-supervised Learning on Graphs

Cristina Garcia-Cardona

, Arjuna Flenner

and Allon G. Percus

Institute of Mathematical Sciences, Claremont Graduate University, Claremont, CA 91711, U.S.A.

Naval Air Warfare Center, Physics and Computational Sciences, China Lake, CA 93555, U.S.A.

Keywords:

Graph Segmentation, Diffuse Interfaces, Learning on Graphs.

Abstract:

We present a graph-based variational algorithm for multiclass classiﬁcation of high-dimensional data, moti-

vated by total variation techniques. The energy functional is based on a diffuse interface model with a periodic

potential. We augment the model by introducing an alternative measure of smoothness that preserves sym-

metry among the class labels. Through this modiﬁcation of the standard Laplacian, we construct an efﬁcient

multiclass method that allows for sharp transitions between classes. The experimental results demonstrate that

our approach is competitive with the state of the art among other graph-based algorithms.

1 INTRODUCTION

Many tasks in pattern recognition and machine learn-

ing rely on the ability to quantify local similarities in

data, and to infer meaningful global structure from

such local characteristics (Coifman et al., 2005). In

the classiﬁcation framework, the desired global struc-

ture is a descriptive partition of the data into cate-

gories or classes. Many studies have been devoted

to the binary classiﬁcation problems. The multiple-

class case, where the data is partitioned into more than

two clusters, is more challenging. One approach is

to treat the problem as a series of binary classiﬁca-

tion problems (Allwein et al., 2000). In this paper, we

develop an alternative method, involving a multiple-

class extension of the diffuse interface model intro-

duced in (Bertozzi and Flenner, 2012).

The diffuse interface model by Bertozzi and Flen-

ner combines methods for diffusion on graphs with ef-

ﬁcient partial differential equation techniques to solve

binary segmentation problems. As with other meth-

ods inspired by physical phenomena (Bertozzi et al.,

2007; Jung et al., 2007; Li and Kim, 2011), it requires

the minimization of an energy expression, speciﬁ-

cally the Ginzburg-Landau (GL) energy functional.

The formulation generalizes the GL functional to the

case of functions deﬁned on graphs, and its minimiza-

tion is related to the minimization of weighted graph

cuts (Bertozzi and Flenner, 2012). In this sense, it par-

allels other techniques based on inference on graphs

via diffusion operators or function estimation (Coif-

man et al., 2005; Chung, 1997; Zhou and Sch

olkopf,

2004; Szlam et al., 2008; Wang et al., 2008; B

uhler

and Hein, 2009; Szlam and Bresson, 2010; Hein and

Setzer, 2011).

Multiclass segmentation methods that cast the

problem as a series of binary classiﬁcation problems

use a number of different strategies: (i) deal di-

rectly with some binary coding or indicator for the la-

bels (Dietterich and Bakiri, 1995; Wang et al., 2008),

(ii) build a hierarchy or combination of classiﬁers

based on the one-vs-all approach or on class rank-

ings (Hastie and Tibshirani, 1998; Har-Peled et al.,

2003) or (iii) apply a recursive partitioning scheme

consisting of successively subdividing clusters, until

the desired number of classes is reached (Szlam and

Bresson, 2010; Hein and Setzer, 2011). While there

are advantages to these approaches, such as possible

robustness to mislabeled data, there can be a consid-

erable number of classiﬁers to compute, and perfor-

mance is affected by the number of classes to parti-

tion.

In contrast, we propose an extension of the diffuse

interface model that obtains a simultaneous segmen-

tation into multiple classes. The multiclass extension

is built by modifying the GL energy functional to re-

move the prejudicial effect that the order of the la-

belings, given by integer values, has in the smoothing

term of the original binary diffuse interface model. A

new term that promotes homogenization in a multi-

class setup is introduced. The expression penalizes

data points that are located close in the graph but are

Garcia-Cardona C., Flenner A. and G. Percus A. (2013).

Multiclass Diffuse Interface Models for Semi-supervised Learning on Graphs.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 78-86

DOI: 10.5220/0004268100780086

 SciTePress

not assigned to the same class. This penalty is ap-

plied independently of how different the integer val-

ues are, representing the class labels. In this way, the

characteristics of the multiclass classiﬁcation task are

incorporated directly into the energy functional, with

a measure of smoothness independent of label order,

allowing us to obtain high-quality results. Alterna-

tive multiclass methods minimize a Kullback-Leibler

divergence function (Subramanya and Bilmes, 2011)

or expressions involving the discrete Laplace operator

on graphs (Zhou et al., 2004; Wang et al., 2008).

This paper is organized as follows. Section 2 re-

views the diffuse interface model for binary classiﬁca-

tion, and describes its application to semi-supervised

learning. Section 3 discusses our proposed multiclass

extension and the corresponding computational algo-

rithm. Section 4 presents results obtained with our

method. Finally, section 5 draws conclusions and de-

lineates future work.

2 DATA SEGMENTATION WITH

THE GINZBURG-LANDAU

MODEL

The diffuse interface model (Bertozzi and Flenner,

2012) is based on a continuous approach, using the

Ginzburg-Landau (GL) energy functional to measure

the quality of data segmentation. A good segmenta-

tion is characterized by a state with small energy. Let

u(x) be a scalar ﬁeld deﬁned over a space of arbitrary

dimensionality, and representing the state of the sys-

tem. The GL energy is written as the functional

(u) =

|∇u|

dx +

F(u) dx, (1)

with ∇ denoting the spatial gradient operator, ε > 0

a real constant value, and F a double well potential

with minima at ±1:

F(u) =



−1



. (2)

Segmentation requires minimizing the GL func-

tional. The norm of the gradient is a smoothing term

that penalizes variations in the ﬁeld u. The potential

term, on the other hand, compels u to adopt the dis-

crete labels of +1 or −1, clustering the state of the

system around two classes. Jointly minimizing these

two terms pushes the system domain towards homo-

geneous regions with values close to the minima of

the double well potential, making the model appro-

priate for binary segmentation.

The smoothing term and potential term are in con-

ﬂict at the interface between the two regions, with the

ﬁrst term favoring a gradual transition, and the second

term penalizing deviations from the discrete labels. A

compromise between these conﬂicting goals is estab-

lished via the constant ε. A small value of ε denotes a

small length transition and a sharper interface, while

a large ε weights the gradient norm more, leading to

a slower transition. The result is a diffuse interface

between regions, with sharpness regulated by ε.

It can be shown that in the limit ε → 0 this func-

tion approximates the total variation (TV) formulation

in the sense of functional (Γ) convergence (Kohn and

Sternberg, 1989), producing piecewise constant solu-

tions but with greater computational efﬁciency than

conventional TV minimization methods. Thus, the

diffuse interface model provides a framework to com-

pute piecewise constant functions with diffuse tran-

sitions, approaching the ideal of the TV formulation,

but with the advantage that the smooth energy func-

tional is more tractable numerically and can be mini-

mized by simple numerical methods such as gradient

descent.

The GL energy has been used to approximate the

TV norm for image segmentation (Bertozzi and Flen-

ner, 2012) and image inpainting (Bertozzi et al., 2007;

Dobrosotskaya and Bertozzi, 2008). Furthermore, a

calculus on graphs equivalent to TV has been intro-

duced in (Gilboa and Osher, 2008; Szlam and Bres-

son, 2010).

Application of Diffuse Interface Models

to Graphs

An undirected, weighted neighborhood graph is used

to represent the local relationships in the data set. This

is a common technique to segment classes that are

not linearly separable. In the N-neighborhood graph

model, each vertex z

∈ Z of the graph corresponds

to a data point with feature vector x

, while the weight

i j

is a measure of similarity between z

and z

. More-

over, it satisﬁes the symmetry property w

i j

= w

. The

neighborhood is deﬁned as the set of N closest points

in the feature space. Accordingly, edges exist be-

tween each vertex and the vertices of its N-nearest

neighbors. Following the approach of (Bertozzi and

Flenner, 2012), we calculate weights using the local

scaling of Zelnik-Manor and Perona (Zelnik-Manor

and Perona, 2005),

i j

= exp



−

||x

−x

τ(x

) τ(x

)



. (3)

Here, τ(x

) = ||x

−x

|| deﬁnes a local value for each

, where x

is the position of the Mth closest data

point to x

, and M is a global parameter.

MulticlassDiffuseInterfaceModelsforSemi-supervisedLearningonGraphs

It is convenient to express calculations on graphs

via the graph Laplacian matrix, denoted by L. The

procedure we use to build the graph Laplacian is as

follows.

1. Compute the similarity matrix W with compo-

nents w

i j

deﬁned in (3). As the neighborhood re-

lationship is not symmetric, the resulting matrix

W is also not symmetric. Make it a symmetric ma-

trix by connecting vertices z

and z

if z

is among

the N-nearest neighbors of z

or if z

is among the

N-nearest neighbors of z

(von Luxburg, 2006).

2. Deﬁne D as a diagonal matrix whose ith diago-

nal element represents the degree of the vertex z

evaluated as

∑

i j

. (4)

3. Calculate the graph Laplacian: L = D −W .

Generally, the graph Laplacian is normalized to guar-

antee spectral convergence in the limit of large sample

size (von Luxburg, 2006). The symmetric normalized

graph Laplacian L

is deﬁned as

= D

−1/2

L D

−1/2

= I −D

−1/2

W D

−1/2

. (5)

Data segmentation can now be carried out through

a graph-based formulation of the GL energy. To

implement this task, a ﬁdelity term is added to the

functional as initially suggested in (Dobrosotskaya

and Bertozzi, 2010). This enables the speciﬁcation

of a priori information in the system, for example

the known labels of certain points in the data set.

This kind of setup is called semi-supervised learning

(SSL). The discrete GL energy for SSL on graphs can

be written as (Bertozzi and Flenner, 2012):

SSL

(u) =

hu,L

ui+

∑

∈Z

F(u(z

))

∑

∈Z

λ(z

)

(u(z

) −u

))

(6)

In the discrete formulation, u is a vector whose com-

ponent u(z

) represents the state of the vertex z

, ε > 0

is a real constant characterizing the smoothness of

the transition between classes, and λ(z

) is a ﬁdelity

weight taking value λ > 0 if the label u

) (i.e. class)

of the data point associated with vertex z

is known

beforehand, or λ(z

) = 0 if it is not known (semi-

supervised).

Equation (6) may be understood as an example of

the more general form of an energy functional for data

classiﬁcation,

E(u) = ||u||

||u − f ||

, (7)

where the norm ||u||

is a regularization term and

||u − f ||

is a ﬁdelity term. The choice of the reg-

ularization norm ||·||

has non-trivial consequences

in the ﬁnal classiﬁcation accuracy. Attractive quali-

ties of the norm ||·||

include allowing classes to be

close in a metric space, and obtain segmentations for

nonlinearly separable data. Both of these goals are

addressed using the GL energy functional for SSL.

Minimizing the functional simulates a diffusion

process on the graph. The information of the few la-

bels known is propagated through the discrete struc-

ture by means of the smoothing term, while the po-

tential term clusters the vertices around the states ±1

and the ﬁdelity term enforces the known labels. The

energy minimization process itself attempts to reduce

the interface regions. Note that in the absence of the

ﬁdelity term, the process could lead to a trivial steady-

state solution of the diffusion equation, with all data

points assigned the same label.

The ﬁnal state u(z

) of each vertex is obtained by

thresholding, and the resulting homogeneous regions

with labels of +1 and −1 constitute the two-class data

segmentation.

3 MULTICLASS EXTENSION

The double-well potential in the diffuse interface

model for SSL ﬂows the state of the system towards

two deﬁnite labels. Multiple-class segmentation re-

quires a more general potential function F(u) that al-

lows clusters around more than two labels. For this

purpose, we use the periodic-well potential suggested

by Li and Kim (Li and Kim, 2011),

F(u) =

{u}

({u}−1)

, (8)

where {u} denotes the fractional part of u,

{u} = u −buc, (9)

and buc is the largest integer not greater than u.

This periodic potential well promotes a multiclass

solution, but the graph Laplacian term in Equation (6)

also requires modiﬁcation for effective calculations

due to the ﬁxed ordering of class labels in the multi-

ple class setting. The graph Laplacian term penalizes

large changes in the spatial distribution of the system

state more than smaller gradual changes. In a multi-

class framework, this implies that the penalty for two

spatially contiguous classes with different labels may

vary according to the (arbitrary) ordering of the la-

bels.

This phenomenon is shown in Figure 1. Sup-

pose that the goal is to segment the image into three

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

classes: class 0 composed by the black region, class

1 composed by the gray region and class 2 composed

by the white region. It is clear that the horizontal in-

terfaces comprise a jump of size 1 (analogous to a

two class segmentation) while the vertical interface

implies a jump of size 2. Accordingly, the smoothing

term will assign a higher cost to the vertical interface,

even though from the point of view of the classiﬁca-

tion, there is no speciﬁc reason for this. In this ex-

ample, the problem cannot be solved with a different

label assignment. There will always be an interface

with higher costs than others independent of the inte-

ger values used.

Thus, the multiclass approach breaks the sym-

metry among classes, inﬂuencing the diffuse inter-

face evolution in an undesirable manner. Eliminating

this inconvenience requires restoring the symmetry,

so that the difference between two classes is always

the same, regardless of their labels. This objective is

achieved by introducing a new class difference mea-

sure.

Figure 1: Three class segmentation. Black: class 0. Gray:

class 1. White: class 2.

3.1 Generalized Difference Function

The ﬁnal class labels are determined by thresholding

each vertex u(z

), with the label y

set to the nearest

integer:



u(z

) +



. (10)

The boundaries between classes then occur at

half-integer values corresponding to the unstable

equilibrium states of the potential well. Deﬁne the

function ˆr(x) to represent the distance to the nearest

half-integer:

ˆr(x) =



−{x}



. (11)

A schematic of ˆr(x) is depicted in Figure 2. The

ˆr(x) function is used to deﬁne a generalized differ-

ence function between classes that restores symmetry

in the energy functional. Deﬁne the generalized dif-

ference function ρ as:

ρ(u(z

),u(z

)) =







ˆr(u(z

)) + ˆr(u(z

)) y

6= y



ˆr(u(z

)) − ˆr(u(z

))



= y

(12)



aaa

Half-integer

Integer



ˆr(x)

Figure 2: Schematic interpretation of generalized differ-

ence: ˆr(x) measures distance to nearest half-integer, and ρ

then corresponds to distance on tree.

Thus, if the vertices are in different classes, the

difference ˆr(x) between each state’s value and the

nearest half-integer is added, whereas if they are in

the same class, these differences are subtracted. The

function ρ(x,y) corresponds to the tree distance (see

Fig. 2). Strictly speaking, ρ is not a metric since it

does not satisfy ρ(x,y) = 0 ⇒x = y. Nevertheless, the

cost of interfaces between classes becomes the same

regardless of class labeling when this generalized dis-

tance function is implemented.

The GL energy functional for SSL, using the new

generalized difference function ρ, is expressed as

MGL

SSL

(u) =

∑

∈Z

∑

∈Z

i j

[ρ(u(z

),u(z

))]

2ε

∑

∈Z

{u(z

)}

({u(z

)}−1)

∑

∈Z

λ(z

)

(u(z

) −u

))

. (13)

Note that ρ could also be used in the ﬁdelity term,

but for simplicity this modiﬁcation is not included. In

practice, this has little effect on the results.

3.2 Computational Algorithm

The GL energy functional given by (13) may be min-

imized iteratively, using gradient descent:

m+1

= u

−dt



δE

MGL

SSL

δu



, (14)

where u

is a shorthand for u(z

), dt represents the

time step and the gradient direction is given by:

δE

MGL

SSL

δu

= εG(u

)+λ

−u

) (15)

G(u

) =

∑

i j



ˆr(u

) ± ˆr(u

)



ˆr

) (16)

) = 2 {u

}

−3 {u

}

+ {u

} (17)

The gradient of the generalized difference function ρ

is not deﬁned at half integer values. Hence, we mod-

MulticlassDiffuseInterfaceModelsforSemi-supervisedLearningonGraphs

Algorithm 1: Calculate u.

Require: ε > 0, dt > 0,m

max

> 0,K given

Ensure: out = u

max

← rand((0,K)) −

, m ←0

for m < m

max

i ← 0

for i < n do

m+1

← u

−dt



ε G(u

) +

) + λ

−u

)



if Label(u

m+1

) 6= Label(u

) then

)

← k + {u

m+1

}

m+1

← (v

)

where k = arg min

0≤k<K

∑

i j

√

[ρ((v

)

)]

end if

i ← i + 1

end for

m ← m + 1

end for

ify the method using a greedy strategy: after detecting

that a vertex changes class, the new class that min-

imizes the smoothing term is selected, and the frac-

tional part of the state computed by the gradient de-

scent update is preserved. Consequently, the new state

of vertex i is the result of gradient descent, but if this

causes a change in class, then a new state is deter-

mined.

Speciﬁcally, let k represent an integer in the range

of the problem, i.e. k ∈[0,K −1], where K is the num-

ber of classes in the problem. Given the fractional

part {u} resulting from the gradient descent update,

deﬁne (v

)

= k + {u

}. Find the integer k that mini-

mizes

∑

i j

√

[ρ((v

)

)]

, the smoothing term in

the energy functional, and use (v

)

as the new vertex

state. A summary of the procedure is shown in Algo-

rithm 1 with m

max

denoting the maximum number of

iterations.

4 RESULTS

The performance of the multiclass diffuse interface

model is evaluated using a number of data sets from

the literature, with differing characteristics. Data and

image segmentation problems are considered on syn-

thetic and real data sets.

4.1 Synthetic Data

A synthetic three-class segmentation problem is

constructed following an analogous procedure used

in (B

uhler and Hein, 2009) for “two moon” bi-

nary classiﬁcation, using three half circles (“three

moons”). The half circles are generated in R

. The

two top circles have radius 1 and are centered at (0, 0)

and (3,0). The bottom half circle has radius 1.5

and is centered at (1.5, 0.4). We sample 1500 data

points (500 from each of these half circles) and em-

bed them in R

100

. The embedding is completed by

adding Gaussian noise with σ

= 0.02 to each of the

100 components for each data point. The dimension-

ality of the data set, together with the noise, make this

a nontrivial problem.

The difﬁculty of the problem is illustrated in Fig-

ure 3, where we use both spectral clustering decompo-

sition and the multiclass GL method. The same graph

structure is used for both methods. The symmetric

graph Laplacian is computed based on edge weights

given by (3), using N = 10 nearest neighbors and lo-

cal scaling based on the M = 10 closest point. The

spectral clustering results are obtained by applying a

k-means algorithm to the ﬁrst 3 eigenvectors of the

symmetric graph Laplacian. The average error ob-

tained, over 100 executions of spectral clustering, is

20% (±0.6%). The ﬁgure displays the best result ob-

tained, corresponding to an error of 18.67%.

The multiclass GL method was implemented with

the following parameters: interface scale ε = 1, step

size dt = 0.01 and number of iterations m

max

= 800.

The ﬁdelity term is determined by labeling 25 points

randomly selected from each class (5% of all points),

and setting the ﬁdelity weight to λ = 30 for those

points. Several runs of the procedure are performed

to isolate effects from the random initialization and

the arbitrary selection of ﬁdelity points. The aver-

age error obtained, over 100 runs with four differ-

ent ﬁdelity sets, is 5.2% (±1.01%). In general terms,

the system evolves from an initially inhomogeneous

state, rapidly developing small islands around ﬁdelity

points that become seeds for homogeneous regions

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

Figure 3: Three-class segmentation. Left: spectral clustering. Right: multiclass GL (adaptive ε).

and progressing to a conﬁguration of classes forming

nearly uniform clusters.

The multiclass results were further improved by

incrementally decreasing ε to allow sharper transi-

tions between states as in (Bertozzi and Flenner,

2012). With this approach, the average error obtained

over 100 runs is reduced to 2.6% (±0.3%). The best

result obtained in these runs is displayed in Figure 3

and corresponds to an average error of 2.13%. In

these runs, ε is reduced from ε

= 2 to ε

= 0.1 in

decrements of 10%, with 40 iterations performed per

step. The average computing time per run in this

adaptive technique is 1.53s in an Intel Quad-Core @

2.4 GHz, without any parallel processing.

For comparison, we note the results from the liter-

ature for the simpler two moon problem (R

100

, σ

0.02 noise). The best errors reported include: 6% for

p-Laplacian (B

uhler and Hein, 2009), 4.6% for ratio-

minimization relaxed Cheeger cut (Szlam and Bres-

son, 2010), and 2.3% for binary GL (Bertozzi and

Flenner, 2012). While these are not SSL methods the

last of these does involve other prior information in

the form of a mass balance constraint. It can be seen

that both of our procedures, ﬁxed and adaptive ε, pro-

duce high-quality results even for the more complex

three-class segmentation problem. Calculation times

are also competitive with those reported for the binary

case (0.5s - 50s).

4.2 Image Segmentation

As another test setup, we use a grayscale image of

size 191 ×196, taken from (Jung et al., 2007; Li and

Kim, 2011) and composed of 5 classes: black, dark

gray, medium gray, light gray and white. This image

contains structure, such as an internal hole and junc-

tions where multiple classes meet. The image infor-

mation is represented through feature vectors deﬁned

as (x

,pix

), with x

and y

corresponding to (x, y)

coordinates of the pixel and pix

equal to the inten-

sity of the pixel. All of these are normalized so as to

obtain values in the range [0,1].

The graph is constructed using N = 30 nearest

neighbors and local scaling based on the M = 30 clos-

est point. We use parameters ε = 1, dt = 0.01 and

max

= 800. We then choose 1500 random points (4%

of the total) for the ﬁdelity term, with λ = 30. Fig-

ure 4 displays the original image with the randomly

selected ﬁdelity points (top left), and the ﬁve-class

segmentation. Each class image shows in white the

pixels identiﬁed as belonging to the class, and in black

the pixels of the other classes. In this case, all the

classes are segmented perfectly with an average run

time of 59.7s. The method of Li and Kim (Li and

Kim, 2011) also segments this image perfectly, with

a reported run time of 0.625s. However, their ap-

proach uses additional information, including a pre-

assignment of speciﬁc grayscale levels to classes, and

the overall densities of each class. Our approach does

not require these.

4.3 MNIST Data

The MNIST data set available at http://

yann.lecun.com/exdb/mnist/ is composed of 70,000

images of size 28 × 28, corresponding to a broad

sample of handwritten digits 0 through 9. We use

the multiclass diffuse interface model to segment

the data set automatically into 10 classes, one per

handwritten digit. Before constructing the graph, we

preprocess the data by normalizing and projecting

into 50 principal components, following the approach

in (Szlam and Bresson, 2010). No further steps, such

as smoothing convolutions, are required. The graph

is computed with N = 10 nearest neighbors and local

scaling based on the M = 10 closest points.

An adaptive ε variant of the algorithm is imple-

mented, with parameters ε

= 2, ε

= 0.01, ε decre-

ment 10%, dt = 0.01, and 40 iterations per step. For

the ﬁdelity term, 7,000 images (10% of total) are cho-

sen, with weight λ = 30. The average error obtained,

over 20 runs with four different ﬁdelity sets, is 7%

MulticlassDiffuseInterfaceModelsforSemi-supervisedLearningonGraphs

Figure 4: Image Segmentation Results. Top left: Original ﬁve-class image, with randomly chosen ﬁdelity points displayed.

Other panels: the ﬁve segmented classes, shown in white.

(±0.072%). The confusion matrix for the best result

obtained, corresponding to a 6.86% error, is given in

Table 1: each row represents the segmentation ob-

tained, while the columns represent the true digit la-

bels. For reference, the average computing time per

run in this adaptive technique is 132s. Note that, in

the segmentations, the largest mistakes made are in

trying to distinguish digits 4 from 9 and 7 from 9.

For comparison, errors reported using unsu-

pervised clustering algorithms in the literature

are: 12.9% for p-Laplacian (B

uhler and Hein,

2009), 11.8% for ratio-minimization relaxed Cheeger

cut (Szlam and Bresson, 2010), and 12.36% for the

multicut version of the normalized 1-cut (Hein and

Setzer, 2011). A more sophisticated graph-based

diffusion method applied in a semi-supervised setup

(transductive classiﬁcation), with function-adapted

eigenfunctions, a graph constructed with 13 neigh-

bors, and self-tuning with the 9th neighbor reported

in (Szlam et al., 2008) obtains an error of 7.4%. Re-

sults with similar errors are reported in (Liu et al.,

2010). Thus, the performance of the multiclass GL

on this data set improves upon other published results,

while requiring less preprocessing and a simpler reg-

ularization of the functions on the graph.

5 CONCLUSIONS

We have proposed a new multiclass segmentation pro-

cedure, based on the diffuse interface model. The

method obtains segmentations of several classes si-

multaneously without using one-vs-all or alterna-

tive sequences of binary segmentations required by

other multiclass methods. The local scaling method

of Zelnik-Manor and Perona, used to construct the

graph, constitutes a useful representation of the char-

acteristics of the data set and is adequate to deal with

high-dimensional data.

Our modiﬁed diffusion method, represented by

the non-linear smoothing term introduced in the

Ginzburg-Landau functional, exploits the structure of

the multiclass model and is not affected by the or-

dering of class labels. It efﬁciently propagates class

information that is known beforehand, as evidenced

by the small proportion of ﬁdelity points (4% - 10%

of dataset) needed to perform accurate segmentations.

Moreover, the method is robust to initial conditions.

As long as the initialization represents all classes uni-

formly, different initial random conﬁgurations pro-

duce very similar results. The main limitation of

the method appears to be that ﬁdelity points must be

representative of class distribution. As long as this

holds, such as in the examples discussed, the long-

time behavior of the solution relies less on choosing

the “right” initial conditions than do other learning

techniques on graphs.

State-of-the-art results with small classiﬁcation

errors were obtained for all classiﬁcation tasks. Fur-

thermore, the results do not depend on the particular

class label assignments. Future work includes inves-

tigating the diffuse interface parameter ε. We con-

jecture that the proposed functional converges (in the

Γ-convergence sense) to a total variational type func-

tional on graphs as ε approaches zero, but the exact

nature of the limiting functional is unknown.

ACKNOWLEDGEMENTS

This research has been supported by the Air Force Of-

ﬁce of Scientiﬁc Research MURI grant FA9550-10-1-

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

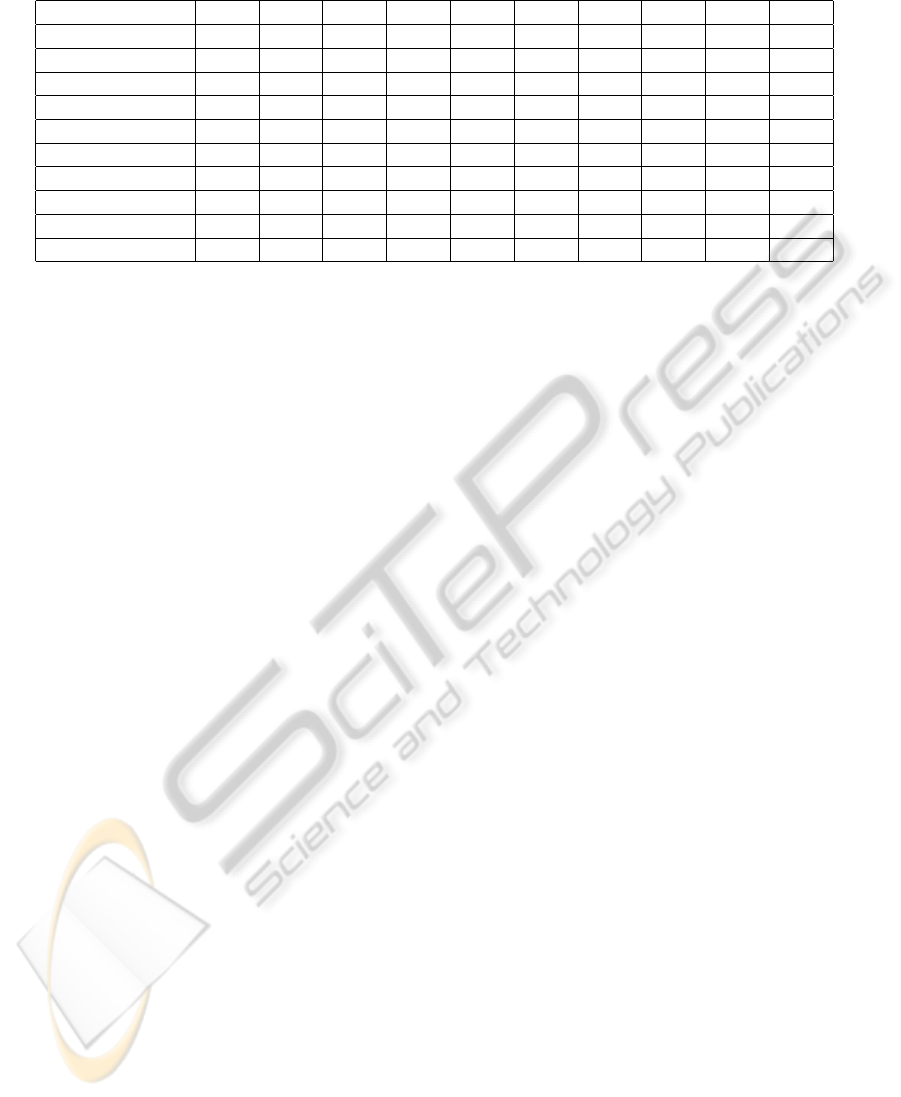
Table 1: Confusion Matrix for the MNIST Data Segmentation.

Obtained / True 0 1 2 3 4 5 6 7 8 9

0 6712 3 39 10 6 36 57 10 61 28

1 1 7738 7 15 9 1 9 23 36 12

2 24 50 6632 95 65 17 16 63 65 30

3 13 16 84 6585 8 218 5 42 153 84

4 5 6 27 8 6279 32 13 59 43 305

5 21 6 13 128 27 5736 57 3 262 34

6 91 26 50 11 35 91 6693 0 45 1

7 6 6 31 97 26 15 0 6689 24 331

8 27 15 86 156 21 110 25 16 6065 66

9 3 11 21 36 348 57 1 388 71 6067

0569 and by ONR grant N0001411AF00002.

REFERENCES

Allwein, E. L., Schapire, R. E., and Singer, Y. (2000). Re-

ducing multiclass to binary: A unifying approach for

margin classiﬁers. Journal of Machine Learning Re-

search, 1:113–141.

Bertozzi, A., Esedo

glu, S., and Gillette, A. (2007). Inpaint-

ing of binary images using the Cahn-Hilliard equation.

IEEE Transactions on Image Processing, 16(1):285–

291.

Bertozzi, A. L. and Flenner, A. (2012). Diffuse inter-

face models on graphs for classiﬁcation of high di-

mensional data. Multiscale Modeling and Simulation,

10(3):1090–1118.

uhler, T. and Hein, M. (2009). Spectral clustering based on

the graph p-Laplacian. In Bottou, L. and Littman, M.,

editors, Proceedings of the 26th International Confer-

ence on Machine Learning, pages 81–88. Omnipress,

Montreal, Canada.

Chung, F. R. K. (1997). Spectral graph theory. In Regional

Conference Series in Mathematics, volume 92. Con-

ference Board of the Mathematical Sciences (CBMS),

Washington, DC.

Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M.,

Nadler, B., Warner, F., and Zucker, S. W. (2005).

Geometric diffusions as a tool for harmonic analy-

sis and structure deﬁnition of data: Diffusion maps.

Proceedings of the National Academy of Sciences,

102(21):7426–7431.

Dietterich, T. G. and Bakiri, G. (1995). Solving multiclass

learning problems via error-correcting output codes.

Journal of Artiﬁcial Intelligence Research, 2(1):263–

286.

Dobrosotskaya, J. A. and Bertozzi, A. L. (2008). A wavelet-

laplace variational technique for image deconvolu-

tion and inpainting. IEEE Trans. Image Process.,

17(5):657–663.

Dobrosotskaya, J. A. and Bertozzi, A. L. (2010). Wavelet

analogue of the Ginzburg-Landau energy and its

gamma-convergence. Interfaces and Free Boundaries,

12(2):497–525.

Gilboa, G. and Osher, S. (2008). Nonlocal operators with

applications to image processing. Multiscale Model-

ing and Simulation, 7(3):1005–1028.

Har-Peled, S., Roth, D., and Zimak, D. (2003). Constraint

classiﬁcation for multiclass classiﬁcation and ranking.

In S. Becker, S. T. and Obermayer, K., editors, Ad-

vances in Neural Information Processing Systems 15,

pages 785–792. MIT Press, Cambridge, MA.

Hastie, T. and Tibshirani, R. (1998). Classiﬁcation by pair-

wise coupling. In Advances in Neural Information

Processing Systems 10. MIT Press, Cambridge, MA.

Hein, M. and Setzer, S. (2011). Beyond spectral clus-

tering - tight relaxations of balanced graph cuts. In

Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F.,

and Weinberger, K., editors, Advances in Neural In-

formation Processing Systems 24, pages 2366–2374.

Jung, Y. M., Kang, S. H., and Shen, J. (2007). Multiphase

image segmentation via Modica-Mortola phase transi-

tion. SIAM J. Appl. Math, 67(5):1213–1232.

Kohn, R. V. and Sternberg, P. (1989). Local minimizers

and singular perturbations. Proc. Roy. Soc. Edinburgh

Sect. A, 111(1-2):69–84.

Li, Y. and Kim, J. (2011). Multiphase image segmentation

using a phase-ﬁeld model. Computers and Mathemat-

ics with Applications, 62:737–745.

Liu, W., He, J., and Chang, S.-F. (2010). Large graph con-

struction for scalable semi-supervised learning. Pro-

ceedings of the 27th International Conference on Ma-

chine Learning.

Subramanya, A. and Bilmes, J. (2011). Semi-supervised

learning with measure propagation. Journal of Ma-

chine Learning Research, 12:3311–3370.

Szlam, A. and Bresson, X. (2010). Total variation and

cheeger cuts. In F

urnkranz, J. and Joachims, T., edi-

tors, Proceedings of the 27th International Conference

on Machine Learning, pages 1039–1046. Omnipress,

Haifa, Israel.

Szlam, A. D., Maggioni, M., and Coifman, R. R. (2008).

Regularization on graphs with function-adapted dif-

fusion processes. Journal of Machine Learning Re-

search, 9:1711–1739.

von Luxburg, U. (2006). A tutorial on spectral clustering.

Technical Report TR-149, Max Planck Institute for

Biological Cybernetics.

MulticlassDiffuseInterfaceModelsforSemi-supervisedLearningonGraphs

Wang, J., Jebara, T., and Chang, S.-F. (2008). Graph trans-

duction via alternating minimization. Proceedings of

the 25th International Conference on Machine Learn-

ing.

Zelnik-Manor, L. and Perona, P. (2005). Self-tuning spec-

tral clustering. In Saul, L. K., Weiss, Y., and Bottou,

L., editors, Advances in Neural Information Process-

ing Systems 17. MIT Press, Cambridge, MA.

Zhou, D., Bousquet, O., Lal, T. N., Weston, J., and

Sch

olkopf, B. (2004). Learning with local and global

consistency. In Thrun, S., Saul, L. K., and Sch

olkopf,

B., editors, Advances in Neural Information Process-

ing Systems 16, pages 321–328. MIT Press, Cam-

bridge, MA.

Zhou, D. and Sch

olkopf, B. (2004). A regularization frame-

work for learning from graph data. In Workshop on

Statistical Relational Learning. International Confer-

ence on Machine Learning, Banff, Canada.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods