On the Characterization of a Speed-boat Motion for Real-time

Motion Cueing

Sergio Casas, Inmaculada Coma, José V. Riera and Marcos Fernández

Institute of Robotics (IRTIC), University of Valencia, Valencia, Spain

Keywords: Real-time Simulation, Virtual Reality, Speed-boat, Motion Characterization, Motion Platform, Inertial Cues.

Abstract: Motion platforms are not uncommon for car and flight VR simulators. However, the same is not true about

watercraft. This paper presents an experimental characterization of a speed-boat in order to understand the

nature and magnitude of a typical small watercraft motion. Unlike other studies, this work focuses on real-

time simulation instead of on boat design issues. The purpose of the study is to guide the future process of

designing and parameterizing a suitable motion platform for a VR application. The characterization is

performed by placing two accelerometers, two gyroscopes, one GPS logger, one digital compass, and one

digital anemometer on a speed-boat at several ranges of motion and maneuvering. We analyze tilt, speed,

wind, steering, angular speed, acceleration and angular acceleration at both frequency and time domains.

Characterization results show that at least a 3-DoF heave-pitch-roll motion platform should be used.

1 INTRODUCTION

Motion platforms have been used since the

beginning of the VR era. However, their use has

been concentrated on flight and car simulators, and

there are, to our knowledge, much fewer approaches

to apply this technology to watercraft. In an effort to

make this technology usable and affordable for the

simulation of small boats, we present an

experimental characterization of a speed-boat. The

information obtained from this work will help us in

the design of the physics model of our simulator,

and in the design and construction of a suitable

motion platform. Unfortunately, we have not found

any related work that tries to characterize the 6

degrees of freedom (DoF) of a watercraft motion

with the purpose to reproduce it with a motion

platform in a real-time simulator. Nonetheless,

similar studies have been previously performed on

other types of vehicles, mainly land and air vehicles.

Although the behaviour of a marine vehicle is

substantially different to those ones, the procedure

could be extrapolated. One of the best works that

deals with the characterization of a vehicle for real-

time simulation is the one performed by G.

Reymond and A. Kemeny (Reymond and Kemeny,

2000). Throughout this paper, we will perform a

similar analysis but on a speed-boat.

The rest of the paper is organized as follows. In

section 2 we describe the sensors. Section 3 deals

with the analysis itself. Finally, section 4

summarizes the conclusions that we can draw from

our analysis.

2 CHARACTERIZATION SET-UP

In order to record the necessary data, we used a

laptop connected to a number of sensors placed on

the boat. In particular, we used two 3-axis

accelerometers, two 3-axis gyroscopes, one GPS

logger, one digital compass, one anemometer, a

microphone and a camera.

The accelerometers and gyroscopes were

Nintendo Wiimotes (with Motion Plus) used to

obtain linear accelerations and angular velocities

respectively. We used two of these devices, as one

was placed at the Center of Mass (CoM), and the

other one was placed on the rudder in order to track

the steering. The GPS logger selected was the Holux

M-241 (Holux, 2009). To ameliorate the effects of

its large vertical error, we used the GPS only to track

motion and speed over the XY plane. As its 1 Hz

update frequency is also quite poor; we can mix

information from the accelerometers and from the

GPS to obtain a better estimation of speed. The

275

Casas S., Coma I., Riera J. and Fernández M..

On the Characterization of a Speed-boat Motion for Real-time Motion Cueing.

DOI: 10.5220/0004272302750278

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 275-278

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

digital compass was an OS3000 (Ocean, 2007). The

anemometer was a Kestrel 4000 (Nielsen, 2009). We

also used a simple digital microphone and a webcam

in order to have the test recorded. The devices were

arranged as explained in Figure 1. As the data

acquired from the sensors was time-stamped, it was

fairly easy to synchronize it.

Figure 1: Sensor placement.

3 ANALYSIS AND RESULTS

In this analysis, we tested a Duarry Brio 620 speed-

boat propelled by a Suzuki DF 140 Four Stroke 140

hp engine. It has a weight of 911 kg and a size of

6.20 x 2.20 x 1.43 meters (length x width x height).

This can be considered an average speed-boat, and

this is the reason why we chose it. The test consisted

on 2030 seconds of boat manoeuvring near the Port

of Barcelona, which can be divided into certain time

zones (see Table 1).

All the calculations and analysis of the collected

data were performed using MATLAB 2009.

3.1 Global Analysis (Ranges)

Virtual vehicles are not critically affected by peak

values of speed, acceleration, or any other physical

magnitude. Nevertheless, as we intend to reproduce

the boat’s motion with a real motion platform with

real physical limits, measured peak values are

important in order to know whether or not our

motion platform will be able to withstand such

limits. Peak values need to be taken with caution for

they are usually the consequence of a precise and

unique moment, but they reveal some information.

Table 2 shows the peak values observed during our

experiments. Our frame of reference follows the X-

right, Y-forward, Z-up convention.

For instance, from this data, we can see that the

boat leans to positive pitch. This is a direct result of

the design and engineering of the speed-boat. Unlike

the pitch angle, roll angle is symmetrical around the

Y axis. Besides, roll maximum value is a little lower

than pitch (positive) peak value. Yaw angle is, not

surprisingly, unbounded.

Table 1: Test chronology.

Range(secs) Description

0-260

Set-up and testing (discarded)

260-440

Docked

440-550

Manoeuvres inside port

550-800

Slow navigation near port

800-980

Progressive acceleration

980-1320

Full-speed navigation

1320-1355

Braking and then stopped

1355-1553

Open sea moderate navigation

1553-1613

Navigation, braking and reverse motion

1613-1770

A variety of manoeuvres

1770-1885

Full speed turning

1930-2030

Stopped at sea

Forward acceleration peaks around 0.4 Gs and -

0.8 Gs. Negative accelerations are related to fluid

braking. Water is a very tough fluid to move

through, and it is able to stop the boat rapidly.

Positive accelerations should be related with engine

propelling. However, a further analysis will reveal

that both are a result of water hits instead of the

engine. Lateral acceleration peaks around ±0.5 G,

which is not much. It is symmetric as expected

because it is produced by turns and water hits.

Vertical acceleration ranges from -2 Gs to 1 G,

which is quite a larger range. This shows that one of

the most noticeable effects of being on a speed-boat

is water hitting when jumping from wave to wave.

Both positive and negative peaks are caused by

water waves hitting the boat. These accelerations are

very short but also very sharp, and thus, noticeable.

Angular velocities are also consistent with the

boat’s motion for they are lower around the Z axis

(yaw) than around the other two. Indeed, a boat

suffers high-frequency rotations around pitch and

roll axes, but although it is able to turn (yaw)

quickly, it cannot reach the angular velocities of the

other two axes. Angular velocity around Y axis is a

little greater (the difference is in fact greater because

of outliers) than around X axis. This is also

consistent with the boat design, because the boat is

longer than wider. Travel speed ranges from a few

knots when travelling backwards to more than 25

knots on forward advance. The boat is not designed

to travel backwards because it tends to sink, so

maximum backward speed is very limited.

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

276

Apparent wind speed ranges from 0 to more than 30

knots. It is similar to forward speed, as expected.

Table 2: Observed ranges.

Magnitude Min Max Units

Yaw

0.0 359.99 °

Pitch

-5.3 +21.73 °

Roll

-19.18 +19.86 °

Forward acceleration

-0.83 +0.42 Gs

Lateral acceleration

-0.45 +0.61 Gs

Vertical acceleration

-2.11 +1.15 Gs

Angular speed X

-118.1 +132.9 °/sec

Angular speed Y

-144.8 +110.9 °/sec

Angular speed Z

-42.6 +58.85 °/sec

Forward speed

-5.64 26.71 knots

Apparent wind speed

0.32 32.46 knots

3.2 Time Domain Analysis

A time-domain analysis of the data reveals some

interesting facts. The first one is that pitch and roll

show a different behaviour. They both depend on

swell and speed, but on a different fashion. While

pitch tends to increase with speed (because the

engine generates an off-axis force that creates a

lifting torque) and gets affected by waves, roll seems

to have an opposite behaviour, because roll is much

higher when the boat is stopped and at swell’s

mercy. To corroborate this, we computed the

Pearson correlation between forward speed and pitch

and the result was 0.826. The roll-speed correlation

was -0.218 that reveals some degree of inverse

correlation.

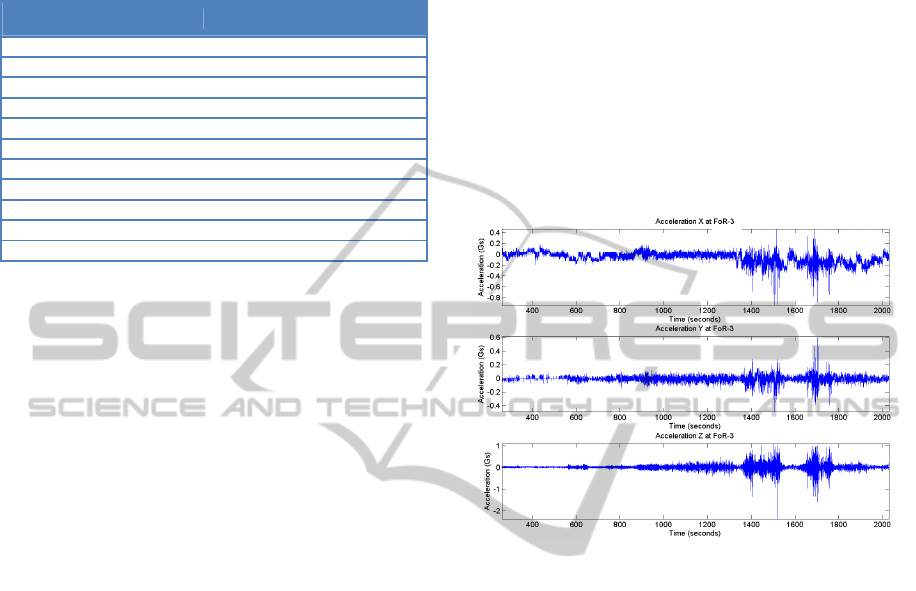
The time-domain analysis of the linear

acceleration reveals that, in spite of testing a speed-

boat with a 140 hp engine, no trace of a sustained Y

acceleration caused by the engine is found. We can

see that in Figure 2 (where we show time vs.

acceleration). Although a speed-boat could reach 30-

40 knots, it takes several seconds to reach that speed,

and the average Y acceleration is even smaller than

that of a utility car. If we compute the average

forward acceleration from 890 to 910 seconds

(maximum acceleration zone) the result is less than

0.2 Gs. The absence of high sustained accelerations

on the Y axis is good for the design of a motion

platform, because sustained accelerations produce

long displacements. X and Z accelerations show a

similar behaviour, although the Z acceleration is

larger and sometimes sharper.

The analysis of the angular acceleration shows

that all three components present a sinusoidal shape,

with some very sharp peaks, that are the result of

water hits, but, again, no trace of sustained angular

acceleration is found. This means that if we want a

motion platform to reproduce X and Y turns, we

need powerful engines to reproduce sharp changes,

but the absence of sustained acceleration assures us

to be within the limits. Regarding the Z axis, there is

some sustained angular speed that indicates that to

simulate that kind of motion we need a motion

platform with as large excursion as possible. In any

case, as the angular accelerations are not sustained

(not even on the Z axis), the motion platform could

trick that with an appropriate washout algorithm

(Reid and Nahon, 1985). For the sake of brevity we

cannot show graphs of all the tested magnitudes.

Figure 2: Linear acceleration.

3.3 Frequency Domain Analysis

Although on time domain we can see the behaviour

on different situations, the analysis of the spectral

distribution of the measures is necessary to asses

which motion cues will be compliant with the future

motion platform rendering performances. The best

way to analyse this is to calculate the cut-off peak-

to-peak maximum displacements. The peak-to-peak

amplitude of the displacement signals were

computed by applying a second-order high-pass

filter of cut-off frequency f



, to the accelerations,

and then double-integrating into positions, exactly

like Reymond and Kemeny did (Reymond and

Kemeny, 2000). The resulting curves of peak-to-

peak amplitudes for different cut-off frequencies are

shown in Figure 3.

As we can see, eliminating all frequencies lower

than 3 Hz the excursion needed for the motion

platform is (22.9, 13.7, 52.7) cm (X, Y, Z) which is

feasible. If we eliminate all frequencies lower than 5

Hz the excursion needs to be (12.3, 7.4, 28) cm,

which could be easier to achieve. As we decrease the

cut-off frequency under the 3 Hz limit, the limits

OntheCharacterizationofaSpeed-boatMotionforReal-timeMotionCueing

277

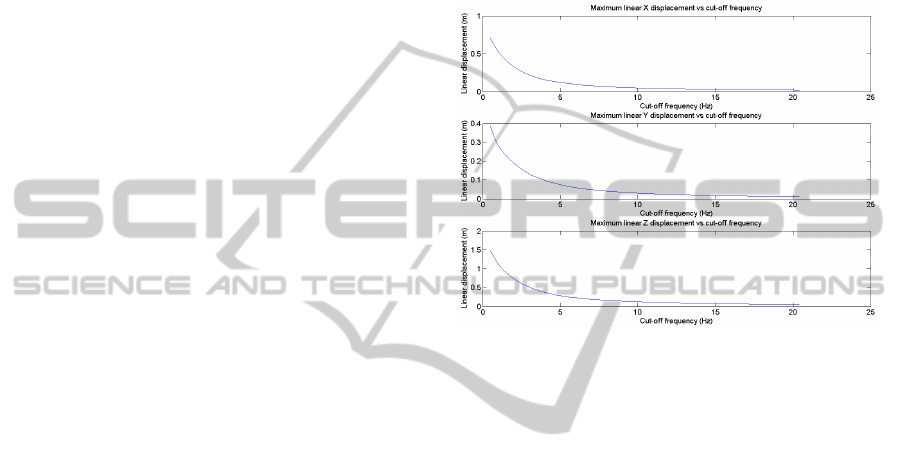
raise exponentially. As we can see, Z excursion

needs to be higher than X and Y. This is a

consequence of the absence of sustained X and Y

accelerations, and also a consequence of sea tide,

which lifts the boat whenever a wave passes under

it, creating a short but more sustained Z motion.

The same can be done with peak-to-peak angles.

In this case, pitch (X) and roll (Y) angles do not

need to be larger than (approximately) 20° and the

yaw angle (Z) is unbounded. This means that pitch

and roll movements could be simulated directly

without filtering provided that the motion platform

withstands those limits (Nahon, 1990). Z turns have

to be filtered because yaw motion is not constrained

but the motion platform usually is. This is consistent

with the measurements of Section 3 and with the

nature of the motion. Following with the analysis,

with a 3 Hz cut-off frequency, the excursion needed

is (12.18, 10.9, 9.4)° (X, Y, Z). With a 5 Hz limit,

the excursion needs to be (10.8, 9.7, 6.6)°, and with

a 10 Hz limit, we need (8.52, 8.53, 3.87)°. Here, an

increase in the cut-off frequency does not change as

much as it did with the translational limits (with the

exception of yaw) and the 3 Hz limit is totally

feasible without losing much information.

4 CONCLUSIONS

Some conclusions can be drawn from our study. On

the qualitative side, we can affirm that the four

major cues when sailing a speed-boat are pitch, wind

speed, roll and heave. Pitch is the major cue because

it is directly linked to the throttle and, at full speed,

considerable pitch angles are reached. Wind speed is

quite important because, unlike in a car, no

windshield protects you from the air, and the feeling

of the wind is fairly intense. Roll is less significant

at high speeds but when the boat is turning or

stopped, it is also quite noticeable. And heave is also

important when the boat hits a wave. These

qualitative conclusions are consistent with our data.

On the quantitative side, the most important

conclusion is that sustained accelerations (low

frequencies) are rather small and that water, and not

the propeller, is the main cause of inertial cues. This

is a significant result because it means that it is more

important to be able to produce fast but sharp

movements than long accelerations. Therefore, the

motion platform excursions do not have to be very

long. However, the engines should be strong enough

to move the platform as quickly as possible. Another

conclusion that can be extracted is that motion along

Z axis is the most important of the linear motions.

As aforementioned, pitch and roll rotations also

reveal very important, because they change sharply

and they define the behaviour of the boat. On the

contrary, yaw rotations tend to be less important

compared to the former. Thus, if we were to choose

a motion platform design, we would build a 3-DoF

pitch-roll-heave motion platform. In our opinion,

this is the minimum necessary to reproduce the

major inertial cues of the boat.

Figure 3: Cut-off peak-to-peak maximum linear

displacements.

Future work includes, of course, building a

suitable motion platform and a real-time simulator to

use it. Some of the future work is already published

in (Casas et al., 2012).

REFERENCES

HOLUX Technology Inc. Holux M-241 Spec., 2009. Web

page: http://www.holux.com/JCore/en/products/

products_spec.jsp?pno=341. Visited: 07/2012.

Nahon, M.A. and Reid, L.D., 1990. Simulator Motion

Drive Algorithms: A Designer’s Perspective. In

Journal of Guidance, Control, and Dynamics, Vol. 13,

No. 2. , pp. 356-362.

Nielsen Kellerman (Kestrel official site), 2009. Kestrel

4000 Data Sheet. http://www.nkhome.com/

pdfs/Kestrel_specs.pdf. Visited: 07/2011.

Ocean Server Technology Inc. ,2007. OS3000 Features.

http://www.oceanserver.com/download/Release_OSI_

060107.pdf. Visited 07/2012.

Reid, L.D. and Nahon, M.A., 1985. Flight Simulation

Motion-Base Drive Algorithms: Part 1 – Developing

and Testing the Equations. In UTIAS Report No. 296.

Reymond, G. and Kemeny, A., 2000. Motion cueing in the

Renault Driving Simulator. In Vehicle System

Dynamics, pp. 249-259.

Casas S. et al., 2012. On the Real-time Physics Simulation

of a Speed-boat Motion. In GRAPP 2012, pp. 121-128

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

278