The Case for Physics Visualization in an Animator’s Toolset

Ari Shapiro and Andrew W. Feng

Institute For Creative Technologies, University of Southern California, Los Angeles, U.S.A.

Keywords:

Physical Simulation, Character Animation.

Abstract:

By associating physical properties with a digital character’s joint and bones, we are able to visualize explicitly

a number of properties that can help animators develop high-quality animation. For example, proper ballistic

arcs can be shown to demonstrate proper timing and location of a character during ﬂight. In addition, a

center of mass that accurately reﬂects the posture of the character can be shown to help with a balanced

appearance during walking or running. In addition, motion properties not previously considered, such as

angular momentum, can be easily identiﬁed when blatantly violated by an animator. However, very few in-

house or commercial system employ such tools, despite their nearly transparent use in an animator’s workﬂow

and their utility in generating better-quality motion. In this paper, we argue the case for incorporating such

toolset, describe an algorithm for implementing the tools, and detail that types of uses for such a tool.

1 MOTIVATION

Techniques for animating characters in both visual ef-

fects and fully digital features have seen only incre-

mental improvement in the recent past. While high

quality motion, such as that generated via motion cap-

ture, can be used under limited circumstances, much

character animation is still created through hand-

constuction by animators, often using video or motion

capture as reference. The resulting motion quality

of character animation varies greatly according to the

skill of the artist; expert animators can produce high-

quality motion, while novice animators often produce

low-quality motion. The tools traditionally used for

generating character animation have changed very lit-

tle; curve editors, key-framing capabilities and in-

verse kinematics chains. Many animation passes are

required in order to convincingly animate the proper

parts of the character with increasing amounts of de-

tail. These traditional tools are focussed on kinematic

movement; movement of a character in space over

time, and generally do not restrict the ability of the

animator to create any arbitrary movement, even non-

physical ones. The ﬂexibility of these animation tools

make it quite easy for even a non-skilled user to pro-

duce some kind of character movement, albeit low in

quality. The high quality character animation seen

in visual effects and 3D scenes is produced through

painstaking efforts of coordinating movements of the

character’s joints by restricting such movements to

those that appear natural or appropriate the scene.

In fact, great efforts are spent to make characters

appear balanced in their poses, ﬂuid in their move-

ments, and to demonstrate an implied sense of mass.

Many seminal animation principles such as squash-

and-stretch, anticipation and follow-through are in-

tended to guide animators towards generating motion

that loosely obeys the laws of physics, since doing

so has been shown to produce more pleasing anima-

tion results. Oddly, very few of such tool sets have

attempted to incorporate physical parameters explic-

itly, such as body masses, moments of inertia. By

including these physical parameters into an anima-

tor’s toolset, an animator can get explicit feedback to-

wards generating motion that better adheres to the ba-

sic principles of animation. For example, consider the

following exerpt from Richard Williams’ ”The An-

imator’s Survival Kit” p. 36 (Williams, 2009)when

explaining the principle of spacing by using a bounc-

ing ball:

”The ball overlaps itself when it’s at the slow part

of the arc, but when it drops fast, it’s spaced further

apart. That’s the spacing. The spacing is how close or

far apart those clusters are. That’s it. It’s simple, but

it’s important. The spacing is the tricky part. Good

animation spacing is a rare commodity.”

Here Williams points out that it is difﬁcult to do

spacing well through traditional hand-drawing meth-

ods. Likewise, it is also difﬁcult, although can be

done more quickly with kinematic toolsets. With-

247

Shapiro A. and W. Feng A..

The Case for Physics Visualization in an Animator’s Toolset.

DOI: 10.5220/0004273702470253

In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information

Visualization Theory and Applications (GRAPP-2013), pages 247-253

ISBN: 978-989-8565-46-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Visualization of physical properties of a digital

character. Shown in blue is the original path generated by

an animator. Shown in red is the path generated by the tools

after consider the mass and moment of inertia of the char-

acter. Note that the timing (knots) and the path are visibly

different from each other. By incoporating such visualiza-

tion tools into an animator’s workﬂow, better coherence be-

tween animations can be achieved, in addition to creating

more plausible motions.

Figure 2: Timing during a jump. Here a monkey jumps

up and down on a giant octopus. The blue line indicates

the original path and timing from the animator. The red

line indicates the proper timing according to physics. The

middle image shows the maximum height of the monkey

during the jump timed according to physics and gravity. The

bottom image shows the maximum height of the monkey as

determined by the animator. Note that the poses created

by the animator remain intact and are not changed by the

physics tools, thus preserving the level of control for the

animator.

out incorporating dynamical information, the anima-

tor would not know either the exact center of mass,

nor the effect of gravity on the ball. The absence

of explicit physical parameters forces the animator to

guess the effect of physics on a character.

2 BACKGROUND

Applying physics to synthesize character animation

is an ongoing research area for computer graphics,

and in recent years has achieved interesting results

(Ye and Liu, 2012; Coros et al., 2011). These tech-

niques vary from creating dynamic control mecha-

nism (Wang et al., 2012; Mordatch et al., 2010),

to using optimization (Liu, 2009; Mordatch et al.,

2012; Jain et al., 2009; McCann et al., 2006), to

machine learning (Levine et al., 2012; Wang et al.,

2008) and even sketching interfaces (Popovi´c et al.,

2003). However, the overall motion quality of such

techniques falls well below the threshold needed for

visual effects or feature ﬁlms. In fact, even motion

capture data is frequently not used directly in feature

ﬁlms since the timing and positioning of each shot is

speciﬁc and subject to the whim of the director or an-

imation lead. Instead, such motion clips are used as a

visual reference, then replicated by an animator digi-

tally. In addition, generating physically valid charac-

ter motion typically requires setting many unintuitive

parameters, as the impact of such settings has a global

effect on the ﬁnal simulation.

In addition, the process of creating animation is

a creative process with a history extending long be-

fore the advent of the digital pipeline. Animators are

trained on a traditional 3D pipeline and toolset, and

changes to such a workﬂow are not easily accepted.

Even when a new method could be used in place of

traditional animation method, there can be resistance

from animators to changing their pipeline unless the

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

248

results both clearly superior and simultaneously re-

quire little or no change in their workﬂow. Thus the

integration into a production pipeline is as important

a factor as is the method itself. An animator requires

a non-invasive tool that does not change his creative

process while providing him enough control over the

ﬁnal outcome. Tight communication between the tool

creators and the users are essential for the tool to be

useful for an animator’s creative process.

Indeed, the animation phase typically runs in a

contrary fashion to the other pipeline phases. For

example, when lighting a scene, the normal lighting

equations would be applied which are roughly based

on physical phenomenae, then later altered to achieve

speciﬁc lighting effects. Thus lighting starts from be-

ing realistic, then changes (perhaps becoming less re-

alistic or less physically-based) to accommodate the

needs of the scene. The same goes for other types

of simulation; a rigid body simulation will be run us-

ing normal physical settings (such as earth-like grav-

ity and non-penetration constraints) and then altered

according to the needs of the scene, perhaps satisfy-

ing fewer physical phenomenae. Even modellers will

start with a scan and texture of a real object, then alter

that object for its speciﬁc use in the shot. By con-

trast, an animator will start from a non-moving char-

acter, then perform rough animation, then slowly re-

ﬁne the animation until it is acceptable for the shot.

Thus, unlike the other pipeline steps, animation starts

from an unrealistic form, and then is fashioned to be-

come more realistic. The effect is that models, par-

ticle effects, lights, backgrounds and other static as-

pects of digital or digitally enhanced scenes can look

highly realistic, yet cartoony,non-plausible animation

is readily identiﬁed on the characters in the scene and

a pervasive aspect of modern digitially produced re-

sults.

To our knowledge, very few efforts have been

done to integrate simulation tools into an animator’s

pipeline to help an animator produce physically real-

istic motions.

3 IMPLEMENTATION OF

PHYSICS VISUALIZATION

INTO AN ANIMATOR’S

WORKFLOW

To implement a physics-based visualization, each of

the character’s joints must be associated with three

additional properties that are not typically present in

most character rigs; mass, moment of inertia and den-

sity. Many character rigs include a rigid skinning, as

opposed to a smooth skinning, where each joint is as-

sociated with a polygonal geometry. By using such a

rig, the calculation of physical properties can be auto-

mated:

• Determine the volume of the polygonal shape

• Determine the mass of the joint/bone by multiply-

ing the density by the volume calculated in Step

• Determine the moment of inertia by sampling the

polygonal object

Note that while this automated method will gener-

ate values for each joint, some adjustments will need

to be made, particularly if the size of the polygonal

geometry associated with each joint is out of propor-

tion with the character’s true dimensions. For ex-

ample, cartoon-like characters can often have large

heads, and assuming that the entire polygonal struc-

ture is of uniform density can yield exagerated re-

sults. Such exaggerations can be determined by ob-

serving the ﬁnal center of mass. A large head will

cause the center of mass to be very high up the char-

acter’s body. Similarly, misproportioned limbs can re-

sult in a wildly varying center of mass during move-

ment. In most cases, adjusting the density of each

joint can bring the relative values of each body part in

better balance with each other.

Details of implementing visualizations of linear

and angular momentum can be found in (Shapiro and

Lee, 2011).

4 ADVANTAGES OF PHYSICS

VISUALIZATION

By incorporating dynamics-based parameters into an

animator’s toolset, new insight is gained into proper

ballistic arcs, conservation of angular momentum,

balance and scaling. This is done by associating a

joint in the skeleton hierarchy with both mass and

moment of inertia. Once such parameters have been

added to a character, the following visualizations can

be seen explicitly by the animator:

1) Proper arcs during ﬂight. The law of conser-

vation of linear momentum implies that all objects

moving through space will fall according to gravity

and their initial velocities, assuming no other forces

affect them in ﬂight. Thus, accurate ballistic paths for

both simple objects, such as balls, or complex objects

such as characters, can be easily generated by an ani-

mator by specifying both a start and an end point. The

tool can then produce physically correct ballistic tra-

jectory through simple computation based on initial

TheCaseforPhysicsVisualizationinanAnimator'sToolset

249

Figure 3: Proper paths as dictate by physics and gravity.

(Left image) An object travels from the red sphere on the

left side to the red sphere on the right side, with each circle

represents the position of the center of mass of the object in

1/24 second increments. Note that there is only one proper

path that travels the distance in exactly one second. (Middle

image) A second path can be designed to move from the

green ball to the red ball, but it will take more time to do

so, since space and time are interconnected. (Right image)

There are an inﬁnite number of paths that can be taken, but

each takes a different amount of time. It is not common

knowlege in the animation community that there is only one

valid time for each ballistic path.

position a, initial velocity b, and gravity g using Eq.

1.Such a tool can be used to rough an animation of

a character jumping or falling from a great height, or

the calculation can be reversed in order to determine

where a character originated from in order to land into

the foreground of a scene.

r(t) = a+ tb+

g (1)

2) Proper timings during ﬂight. While the shape

of a ballistic arc can be reasonably duplicated without

physics-based tools, it is difﬁcult to replicate proper

timing of a character’s movement along such a path.

Thus, while an animator may create a proper path for

a character to follow, the timing may be inconsistent,

or overly slow or fast for the size of the object. In fact,

the idea that space and time are interconnected, and

thus, under realistic conditions, an object has only one

time that is appropriate for a given path, is not widely

known in the animation community, see Figure 3. The

timing of a path contributes greatly to its plausible

effect. Animators have a tendency to exaggerate the

ﬁnal phase of a jump or fall in order to demonstrate

the increased energy of the character during this part

of the movement. Proper timings along ballistic arcs

can be generated that properly match the energy of

the moving characters, while maintaining an energetic

appearance.

3) Proper Center of Mass. Many animation rigs

either implicitly or explicity contain a center point for

the character, meant to indicate the center of mass, or

balance point of the character. However, the true cen-

ter of mass of a character varies according its instan-

taneous pose. For example, if a character is kneeling

with his arms extended, the center of mass of such

a character is in fact outside and in front of his body.

Likewise, during some phases of a jump, a character’s

Figure 4: A character does a ﬂip during a jump. Note that

the original animated path (blue) shows inconsistent move-

ments during the ﬂipping motion. This is caused when the

animator refers to a static center that doesn’t adjust based

on pose changes, rather than the true center of mass. The

physics-based path produces a proper ballistic arc.

center of mass is behind the character (see Figure 5.)

Thus, a proper center of mass varies from frame to

frame, and cannot be considered to be a ﬁxed point.

Thus, showing the center of mass of a character on

the ground in front of them can assist an animator

with balance during high-energy activities, such as

walking or running. In addition, characters can fol-

low realistic-looking paths while doing ﬂips in the air,

see Figure 4. Without a dynamically-changing center-

of-mass, a ﬂipping character will not follow a proper

path.

4) Proper Rotations During Flight. The law of

conservation of angular momentum implies that the

angular momentum of a rotating object will be pre-

served. Practically, this means that the sum of all ro-

tations of a character need to remain constant during

ﬂight phases. Angular momentum can be visualized

by a line segment derived from a vector, showing both

direction and magnitude extending from the center of

mass of the character (see Figure 6.) While there is no

easy method to ﬁx problems with angular momentum,

severe violation of the law of conservation of angu-

lar momentum can be seen through sudden changes

in the direction of the line segment, such as switch-

ing from one direction to the opposite one. Such vi-

olations frequently occur during character jumps for

the following reason; animators are trained to bring

the feet of their characters forward in preparation of

a landing, but are not trained to counterbalance the

forward movement of a character’s legs with move-

ment of the character’s arms in the opposite direc-

tion. Thus, many hand-tuned animations of jumping

character show reverses in the angular momentum of

a character during ﬂight (see Figure 7.). Such sub-

tleties of animation are not easily discerned even by

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

250

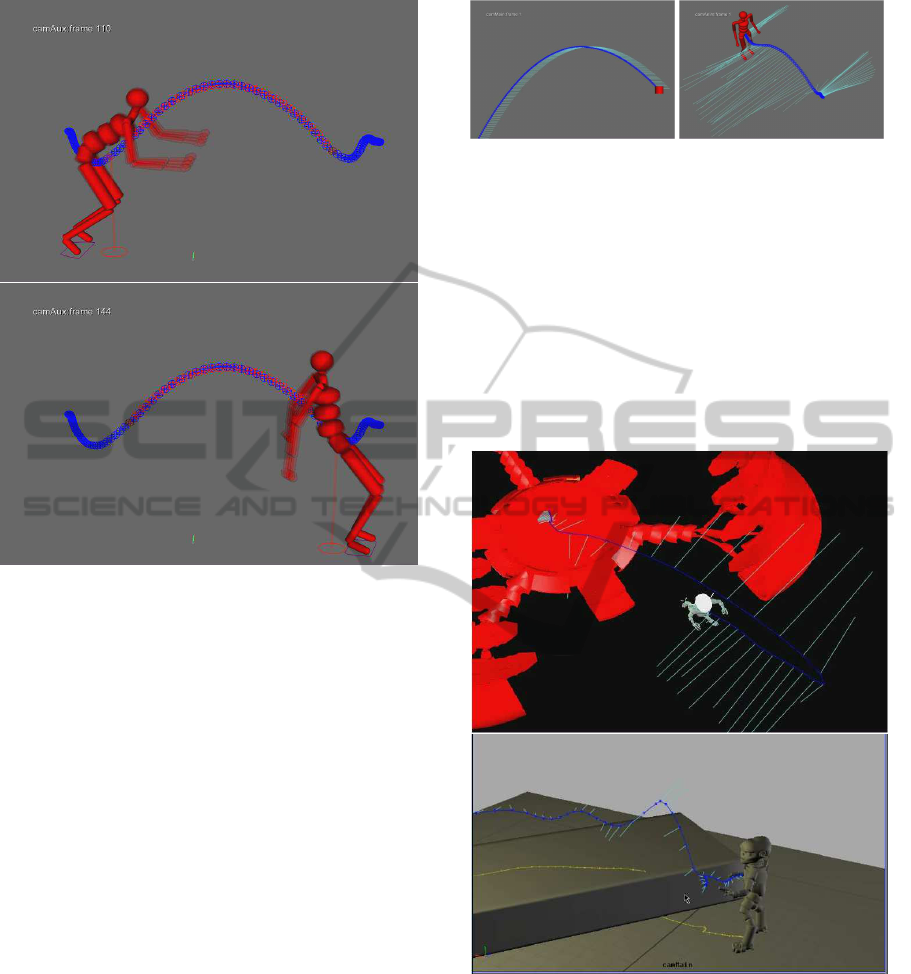
Figure 5: Visualization of a motion-captured jump. The

blue arc indicates the actual path of the characer, while the

red arc indicates the physics-based path according to the

model. (Left image) The red line projecting the the ground

represents the center of mass of the character. Notice that

during the takeoff phase, the center of mass is in front of

the character. (Right image) The character during the land-

ing phase of the jump. Notices that the center of mass is

now behind the character since most of the character’s mass

(arms, torso) are behind the character for a moment during

the last phase of the jump for another frame. This demon-

strates the dynamic nature of a character’s center of mass

that cannot be accurately represented as a ﬁxed point on a

character rig.

highly trained animators, since such rules of physics

are not widely taught. A tool can correct the charac-

ter’s angular momentum h based on velocity v

, iner-

tia J

from each body part i, to the desired momen-

tum h

∗

by adjusting character’s global orientation at

each key frame. However, proper correction of an-

gular momentum requires a greater understanding of

strategies that humans and other animals use to orient

themselves during ﬂight, such as windmilling arms or

other appendages like tails.

5) Proper Treatment of Character Scale. The size

of a character affects the movement of character, and

the speed of movement is used by the human mind to

determine the size of an object. Given two objects that

occupy the same amount of visual space on a screen,

we can determine which one is larger by the speed

Figure 6: (Top image) Visualization of angular momentum

for an object in ﬂight that rotates counter clockwise. An-

gular momentum can be visualized as the blue line segment

representing the axis of rotation extending from the cen-

ter of mass of the object. Note that during the entire ﬂight

phase of the object, the momentum remains in the same di-

rection and is the same length. This indicates that the axis

of rotation is the same, and the momentum doesn’t change.

(Bottom image) Visualization of angular momentum of a

motion-captured character during a jumping motion. Notice

that during the ﬂight phase, the axis of rotation is generally

in the same direction. The magnitude (length) changes, but

this is due to inaccuracies in the physical modeling, and

noise during motion capture.

Figure 7: (Top image) A character is hit with a projectile

and is throw backwards onto the red machine. Notice that

near the end of the motion, the character’s axis of rotation

switches from one side to the other, indicating an impossible

in-ﬂight rotation. Subtleties like this momentum switch can

be easily visualized by animators. (Bottom image) A char-

acter jumps onto a platform. Notice the switch in rotation

direction during ﬂight. This particular example is caused

by failing to bring the arms down to counterbalance moving

the legs forward.

of its movement and the relative speed of movement

of nearby objects. Since gravity affects objects in a

TheCaseforPhysicsVisualizationinanAnimator'sToolset

251

Figure 8: (Left image) A ball being thrown to the height

of 15 feet above a normal-sized person’s head, which takes

slightly more than 2 seconds to complete (Right Image) A

ball being thrown 150 feet above the head of a 60 foot giant,

which takes slightly more than 6 seconds to complete. Note

that we can determine the relative sizes of the characters by

the speed of their motion.

nonlinear way, a simple heuristic can be determined

that indicates how motion should be scaled according

to its size: square root of scale factor. Speciﬁcally,

we can determine the time t required for for an ob-

ject to travel to height h using Eq. 2. In other words,

objects that are four times as large should appear to

move twice as slowly (Pollard, 1999). The correct

treatment of the motion scale is a common pitfall for

an animator. Since animators are most familiar with

motion of a human scale, they usually produce physi-

cally incorrect motions for very large characters. The

impact of this mismatch between size and speed can

be readily seen in numerous feature ﬁlms and clips

that include giant-sized characters, often moving at

the speed of normal-sized ones.

t =

(2)

6) Uniform treatment of characters by numerous

animators. Live-action ﬁlms and animated movies of-

ten utilize dozens of animators in parallel who often

work on the same digital characters in different shots

in order to meet the deadline of the project. Thus,

the movement of a single digital character can be in-

terpreted differently by any number of animators de-

signing their motion. While some processes are set up

in order to reach uniformity, such as dailies sessions,

these processes are often subjective. Physics-based

tools allows each shot to be annotated with various

physical paths, balance points, and momentum mark-

ers. Thus, it can become easier to evaluate the same

character across multiple shots when constructed by

different animators.

7) Synchronization of Digital Character’s With

Live Actors and Physics-Based Effects Often times,

digital characters occupy the same scene as live ac-

tors. Thus, disparities between the quality of motion

of a live actor and a digital actor can be obvious to

the viewer. Thus it is to the animator’s advantage to

understand the impact of real world physics on a live

Figure 9: A large octopus jumping 25 feet across and 15 feet

high into a pool of water. The octopus in this scene is very

large, but is animated as if it is very small, thus violating

physical plausibility. By replacing the giant octopus with a

more familiar object of the same size, the discrepency be-

tween the size of the object and the motion becomes clear

to the animator.

actor, and thus on the digital character as well. In

addition, many visual effects are generated from algo-

rithms that incorporate rules about the physical world,

such as rigid body simulations, water and particle ef-

fects, and so forth. Thus there are occassions where

maintaining a character’s physical validity is impor-

tant to the shot when combined with such effects. For

example, if a character and an object are both mov-

ing through the air, they should obey similar motion

rules.

5 DISCUSSION

The inclusion of physical parameters, such as mass

and moment of inertia into a rigged character can pro-

duce visualizations of the center of mass, linear and

angular momentum and ballistic paths. While phys-

ically valid motion does not always appear more vi-

sually appealling than non-physically valid motion,

there are many cases where it does improve the qual-

ity of perceived motion(Shapiro and Lee, 2011). In

GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications

252

addition, the presence of changes in rotation during

ﬂight can be clearly seen only with the incorpora-

tion of such tools. We believe that increased aware-

ness of problems with angular momentum will re-

sult in higher-quality animations once the animation

community develops rules or guidelines for correct-

ing such problems. In addition, the advent of such

tools into an animator’s pipeline can be done inob-

trusively; a button can be pressed by the animator to

render a non-destructive path against which the cur-

rent animation is compared. The animator still retains

control over all aspects of the animation.

One argument against the use of physics-based

tools in character animation states that a ﬁlm or movie

is an artistic endeavor and the presence of physically-

valid motion does not necessarily make the animation

look more visually appealling. Indeed, it is some-

times desirable to exagerate motion in order to con-

vey a particular character motion or storytelling idea.

While this is true, the ability to compare an animation

against the natural world can lead to better motion

quality quickly under certain circumstances. So while

physically realistic motion is not always needed, it is

helpful to understand it for comparison. In addition,

many classic animation texts refer heavily to physical

phenomenae, and develop rules for mimicking them,

such as squash-and-stretch, anticipation, spacing and

so forth.

The authors have noticed that animators have

expressed the greatest amount of trepidation about

physics-based visualizations when discussing charac-

ters of large scale. Physics-based examples of large

objects and creatures are generally at odds with an an-

imators sense of space and time for large objects. The

authors believe that this is due to a lack of familiarity

with large creatures (such as ﬁfty-foot tall characters)

in the real world. We don’t see giants in this world,

and thus it is difﬁcult to imagine what their move-

ments look like. Thus, large creatures are often ani-

mated as if they are much smaller, often human-sized.

While it is arguable what this motion should look like

from an artistic standpoint, the application of physics

reveals how such creatures would likely move were

they to exist in our world. The authors believe that the

use of such tools for large creatures will result in im-

proved quality motion once these techniques become

widespread.

REFERENCES

Coros, S., Karpathy, A., Jones, B., Reveret, L., and van de

Panne, M. (2011). Locomotion skills for simulated

quadrupeds. ACM Trans. Graph., 30(4):59:1–59:12.

Jain, S., Ye, Y., and Liu, C. K. (2009). Optimization-based

interactive motion synthesis. ACM Transaction on

Graphics, 28(1):1–10.

Levine, S., Wang, J. M., Haraux, A., Popovi´c, Z., and

Koltun, V. (2012). Continuous character control with

low-dimensional embeddings. ACM Transactions on

Graphics, 31(4):28.

Liu, C. K. (2009). Dextrous manipulation from a grasping

pose. ACM Transactions on Graphics (SIGGRAPH),

28(3).

McCann, J., Pollard, N., and Srinivasa, S. (2006). Physics-

based motion retiming. In Proceedings of the 2006

ACM SIGGRAPH/Eurographics symposium on Com-

puter animation, pages 205–214. Eurographics Asso-

ciation.

Mordatch, I., de Lasa, M., and Hertzmann, A. (2010). Ro-

bust physics-based locomotion using low-dimensional

planning. ACM Trans. Graph., 29(4):71:1–71:8.

Mordatch, I., Todorov, E., and Popovi´c, Z. (2012). Discov-

ery of complex behaviors through contact-invariant

optimization. ACM Trans. Graph., 31(4):43:1–43:8.

Pollard, N. (1999). Simple machines for scaling human mo-

tion. In In Proceedings of Computer Animation and

Simulation ’99.

Popovi´c, J., Seitz, S. M., and Erdmann, M. (2003). Motion

sketching for control of rigid-body simulations. ACM

Trans. Graph., 22(4):1034–1054.

Shapiro, A. and Lee, S.-H. (2011). Practical character

physics for animators. Computer Graphics and Ap-

plications, IEEE, 31(4):45 –55.

Wang, J. M., Fleet, D. J., and Hertzmann, A. (2008). Gaus-

sian process dynamical models for human motion.

IEEE Trans. Pattern Anal. Mach. Intell., 30(2):283–

298.

Wang, J. M., Hamner, S. R., Delp, S. L., and Koltun,

V. (2012). Optimizing locomotion controllers us-

ing biologically-based actuators and objectives. ACM

Trans. Graph., 31(4):25:1–25:11.

Williams, R. (2009). The Animator’s Survival Kit–Revised

Edition: A Manual of Methods, Principles and For-

mulas for Classical, Computer, Games, Stop Motion

and Internet Animators. Faber & Faber, Inc.

Ye, Y. and Liu, C. K. (2012). Synthesis of detailed hand

manipulations using contact sampling. ACM Trans.

Graph., 31(4):41:1–41:10.

TheCaseforPhysicsVisualizationinanAnimator'sToolset

253