
Rotationally Invariant 3D Shape Contexts using Asymmetry Patterns
Federico M. Sukno
1,2
, John L. Waddington
2
and Paul F. Whelan
1
1
Centre for Image Processing & Analysis, Dublin City University, Dublin 9, Ireland
2
Molecular and Cellular Therapeutics, Royal College of Surgeons in Ireland, Dublin 2, Ireland
Keywords:
3D Geometric Descriptors, Rotational Symmetry, Craniofacial Landmarks.
Abstract:
This paper presents an approach to resolve the azimuth ambiguity of 3D Shape Contexts (3DSC) based on
asymmetry patterns. We show that it is possible to provide rotational invariance to 3DSC at the expense
of a marginal increase in computational load, outperforming previous algorithms dealing with the azimuth
ambiguity. We build on a recently presented measure of approximate rotational symmetry in 2D defined as the
overlapping area between a shape and rotated versions of itself to extract asymmetry patterns from a 3DSC
in a variety of ways, depending on the spatial relationships that need to be highlighted or disabled. Thus, we
define Asymmetry Patterns Shape Contexts (APSC) from a subset of the possible spatial relations present in
the spherical grid of 3DSC; hence they can be thought of as a family of descriptors that depend on the subset
that is selected. This provides great flexibility to derive different descriptors. We show that choosing the
appropriate spatial patterns can considerably reduce the errors obtained with 3DSC when targeting specific
types of points.
1 INTRODUCTION
Geometric descriptors for three dimensional (3D)
data are important for a wide range of applications,
as they constitute a core element for the identifica-
tion of corresponding points in relation to object re-
trieval (Tombari et al., 2010), recognition (Frome
et al., 2004), surface registration (Bariya et al., 2012)
and landmark identification (Creusot et al., 2011; Pas-
salis et al., 2011).
The increased availability of 3D data in the last
decade has generated much research in this area and
several 3D descriptors have been proposed. Depend-
ing on the data that is targeted, the descriptors can be
purely geometric (Johnson and Hebert, 1999; Rusu
et al., 2009; Zhang, 2009; Chen and Bhanu, 2007)
or include additional functions that are attached to
the geometry, such as radiometric information (Steder
et al., 2011; Zaharescu et al., 2012).
Among purely geometric descriptors, which are
the most general type, 3D shape contexts (and exten-
sions derived from them) have attracted considerable
interest due to their good performance in diverse ap-
plications. Indeed, a recent comparison of geometric
descriptors in the context of craniofacial landmark lo-
calization highlighted 3D shape contexts as one of the
most accurate algorithms (Sukno et al., 2012).
Shape contexts in 3D are based on the distribu-
tion of distances with respect to the point of interest,
estimated by means of a histogram over a spherical
grid (elevation, azimuth and radius). The spherical
grid is centered at the point of interest and its North
Pole is oriented in the direction of the normal to the
surface. This is enough to uniquely determine the el-
evation and radial bins but leaves unresolved the ori-
gin of azimuth bins. Different approaches have been
taken to resolve this ambiguity:
• In one of the earliest works (Frome et al., 2004),
the 3D Shape Contexts descriptor (3DSC) was in-
troduced, without actually resolving the azimuth
ambiguity. The authors compute multiple descrip-
tors to account for all possible rotations (as many
as the number of azimuth bins). During matching,
when comparing descriptors of different points,
all possible rotations are tested and the one that
produces the highest similarity score is retained.
• As an alternative that achieves invariance to the
azimuth angle, Frome et al. explored the use of
Spherical Harmonics. Similarly to other descrip-
tors (Kazhdan et al., 2004), they proposed to keep
only the magnitude of the Spherical Harmonic co-
efficients, which are rotationally invariant. We
will refer to this approach as Harmonic Shape
Contexts (HSC) (Frome et al., 2004).
7
M. Sukno F., L. Waddington J. and F. Whelan P..
Rotationally Invariant 3D Shape Contexts using Asymmetry Patterns.
DOI: 10.5220/0004274600070017
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (GRAPP-2013), pages 7-17
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

• A third option (Kortgen et al., 2003; Tombari
et al., 2010) consists of performing Singular Value
Decomposition (SVD) on the support region (i.e.
all points within the considered sphere) to iden-
tify the principal axes and disambiguate the sign
by considering the heaviest tail of each axis as
the positive direction. Thus, a unique axis can be
identified to set the azimuth origin, obtaining the
Unique Shape Contexts (USC) descriptor.
It would be desirable to avoid the evaluation of
multiple descriptors as done by (Frome et al., 2004).
Such a strategy increases the computational load dur-
ing matching, can suffer from false matches (due to
an unfortunate rotation of the descriptor of a non-
corresponding point) and adds considerable complex-
ity to the application of machine learning techniques
that can be useful upon the availability of a training
set. Despite the above efforts to obtain shape context
descriptors without azimuth ambiguity, the best per-
formance is still obtained by using 3DSC (i.e. com-
puting multiple descriptors).
The performance of HSC was found comparable
to 3DSC in some cases (Frome et al., 2004) but at
the expense of a huge increase in computational load.
On the other hand, USC was reported to perform
slightly better than 3DSC in terms of precision-recall
curves for a task of feature matching on synthetically
transformed shapes (Tombari et al., 2010). However,
USC was found considerably less accurate than 3DSC
when targeting specific points on a craniofacial land-
mark localization task (Sukno et al., 2012). As we
will show, this can be explained by the instability of
the sign disambiguation on objects that present a high
variability, such as the human face. That is, the di-
rection of the axes determined by the proposed dis-
ambiguation step cannot be assured to be consistent
across a population of facial scans. Since USC rely
on the unique definition of the azimuth bins, the lack
of consistency has an important effect on accuracy.
In this paper we present a different approach to re-
solve the azimuth ambiguity based on asymmetry pat-
terns and show that it is possible to attain rotationally
invariant shape contexts that obtain comparable accu-
racy to 3DSC for the localization of craniofacial land-
marks and remarkably outperform 3DSC for specific
points like the outer eye corners and nose corners.
We build on a recently presented measure of ap-
proximate rotational symmetry in 2D (Guo et al.,
2010), defined as the overlapping area between a
shape and rotated versions of itself. We show that
such a measure can be extended to 3DSC and derive
asymmetry based on the absolute differences between
overlappingbins of the descriptorand rotated versions
of itself. Both measures depend of the rotation angle
but not on the selection of the origin of azimuth bins,
which allows us to obtain patterns that capture the ro-
tational asymmetry of the descriptor over the azimuth
but are invariant to the rotation of its bins.
The asymmetry patterns can be defined in a va-
riety of ways, depending on the spatial relationships
that need to be highlighted or disabled. Thus, we
define Asymmetry Patterns Shape Contexts (APSC)
from a subset of the possible spatial relations present
in the spherical support region; hence they can be
thought of as a family of descriptors that depend on
the subset that is selected.
Concrete examples of APSC are evaluated by
defining some of the simplest possible spatial pat-
terns. We show that the performance of APSC de-
pends heavily on the selection of these spatial pat-
terns, which can be useful to target different types
of points. Regarding the complexity, the computa-
tion of an APSC descriptor is slightly more expen-
sive than a single 3DSC but produces considerable
savings at matching time (due to the rotational in-
variance) and memory (APSC requires half the mem-
ory of 3DSC). This computationalefficiencycontrasts
with prior work exploring the use of symmetry in geo-
metric descriptors using Spherical Harmonics (Kazh-
dan et al., 2004)
In the next section we provide the definition of
APSC as well as a brief review of 3DSC. Experimen-
tal evaluation is presented in Section 3, followed by
a discussion of results (Section 4) and concluding re-
marks (Section 5).
2 ASYMMETRY PATTERNS
SHAPE CONTEXTS
Computation of the APSC descriptor starts by com-
puting a 3DSC descriptor (Frome et al., 2004), from
which the asymmetry patterns are later extracted.
2.1 3D Shape Contexts
This descriptor is based on a 3D-histogram computed
on a spherical support region centered at the interest
point, v, considering a neighborhood N
v
= {w|kw−
vk ≤ r
N
}, namely all points within a radius r
N
. The
North pole of the sphere is oriented with the normal
vector at the interest point n
v
. The default structure
has N
E
= 11 elevation bins and N
A
= 12 azimuth bins,
both uniformly spaced, and N
R
= 15 radial bins loga-
rithmically spaced as follows:
r
k
= exp
ln(r
min
) +
k
N
R
ln
r
N
r
min
(1)
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
8

where r
k
is the k-th radial division from a total of N
R
,
r
N
is the radius of the spherical neighborhood and r
min
is the radius of the smallest bin.
The logarithmic sampling is aimed at assigning
more importance to shape changes that are closer to
the interest point. The contribution to the histogram
of a point w that falls in bin (i, j,k) will be:
ρ
w
3
p
V
i, j,k
−1
(2)
where i, j and k are the indices of elevation, azimuth
and radial bins, respectively. The normalization by
bin volume, V
i, j,k
, accounts for the large difference
between bin sizes (especially along radius and eleva-
tion), while the inverse local point density ρ
w
aims to
correct variations in sampling density and is estimated
as the count of points in a small sphere centered at w.
As the spherical support region is defined based
on v and n
v
, there is an ambiguity in the origin of
the azimuth bins. This is dealt with by calculating N
A
descriptors per point, covering all possible shifts. The
computation of multiple descriptors is done for the
model (i.e. during training), so that during matching
only one descriptor is computed and matched to the
multiple descriptors by choosing the one that yields
the smallest Euclidean distance:
d(x, y) = min
0≤a<N
A
v
u
u
t
N
E
−1
∑
i=0
N
A
−1
∑
j=0
N
R
−1
∑
k=0
(x
i, j+a,k
− y
i, j,k
)
2
(3)
where x and y are the descriptors to compare and
the addition j + a is modulo N
A
(i.e circular) so that
x
i, j+a,k
is an azimuth rotation of x
i, j,k
(i.e. about the
North-South axis of the sphere) by a bins.
2.2 Rotational Symmetry
In a recent work, Guo et al. (Guo et al., 2010)
presented continuous measures of approximate bilat-
eral and rotational symmetry. Specifically, given a
shape m in 2D and a rotation angle φ about the z-axis
(i.e. perpendicular to the plane containing the shape),
they defined the rotational central symmetry degree
S
c
(m,φ) to be the area of intersection of shape m with
a rotated version of itself by an angle φ, R(m,φ), nor-
malized by the area of shape m:
S
c
(m,φ) =
Area(m ∩ R(m,φ))
Area(m)
(4)
Defined in this way, S
c
(m,φ) measures the degree of
rotational symmetry of shape m from 0 (no symme-
try) to 1 (perfect symmetry at the considered angle).
We can adapt this symmetry measure to the 3DSC
descriptor by convertingthe area overlapinto the min-
imum value of overlapping bins. That is, as the sup-
port region of the descriptor is spherical, the overlap
of rotated shapes (in terms of area or volume) is al-
ways perfect, but not the values assigned to the coin-
ciding bins. For example, assume we extract from a
3DSC descriptor x the ring composed by all the bins
at a given elevation i and radius k; this will generate a
shape m represented as a sequence of N
A
non-negative
values from the corresponding bins:
m
j
= x
i, j,k
, m
j
≥ 0∀ j ∈ [1;N
A
] (5)
We can define the symmetry degree of the sequence
m as follows:
S (m,a) =
∑
j
min(m
j
,m
j+a
)
∑
j
m
j
(6)
where, as before, j + a is the addition modulo the car-
dinality of m (N
A
in this example).
Notice that the angular parameter φ used in the
area-based definition is replaced by the shift parame-
ter a, which represents a discrete azimuth rotation of
2π/N
A
. Thus, S behaves analogously to S
c
.
Figure 1 shows an example sequence m that corre-
sponds to a ring with perfect rotational symmetry ev-
ery 120 degrees and the sequence resulting from the
concatenation of the symmetry degree for all possible
discrete rotations:
P
S
(m) = S (m,1),S (m,2),.. . ,S (m,N
A
) (7)
The sequence P
S
(m) is the symmetry pattern of the
sequence m which indicates how symmetric is the
ring that originated m for different angles of azimuth
rotation. However, from the definition of S (m,a), it
is clear that the generated pattern is invariant to the
origin chosen for the azimuth bins, i.e.
P
S
(m) = P
S
(R(m,a)),∀a ∈ Z (8)
Circular plot
of the sequence
0 90 180 270 360
0
0.5
1
Sequence values
0 90 180 270 360
0.4
0.6
0.8
1
Azimuth rotation [deg]
Symmetry degree
Figure 1: Example of a sequence with perfect rotational
symmetry at shifts of 120 degrees. A circular representation
is provided on the left by varying the distance to the centre
proportionally to the sequence values, which are shown on
the top-right plot. The bottom-right plot shows the resulting
symmetry pattern.
RotationallyInvariant3DShapeContextsusingAsymmetryPatterns
9

2.3 Asymmetry Patterns
It is interesting to define asymmetry as the comple-
ment of symmetry, also between 0 and 1, as follows:
A (m,a) = 1 − S (m,a) (9)
In the Appendix we show that this definition implies:
A (m,a) =
1
2
∑
j
|m
j
− m
j+a
|
∑
j
m
j
(10)
which is the mean of absolute differences between m
and R(m,a) with an appropriate normalization factor.
While such normalization is important to facilitate a
meaningful interpretation of the asymmetry value in
[0;1], it is not desirable in our case as it removes po-
tentially useful information. Thus we define:
A
1
(m,a) =
∑
j
|m
j
− m
j+a
| (11)
As stated above, this measure captures the average
difference between bins of the sequence originated
from a ring and one azimuth-rotated version of itself.
However, other functions of |m
j
−m
j+a
| would be ap-
plicable, with the only requisite being that they are
summations over all the elements of the sequence. For
example, it would be possible to use the central mo-
ments of any order (indeed our definition of A
1
is a
scaled version of the first-order moment).
We will restrict ourselves to the use of asymmetry
as defined in (12). Considering all possible azimuth
rotations of the sequence that generate distinct values,
we obtain the following asymmetry pattern:
P
A
(m) = A
1
(m,1),A
1
(m,2),.. ., A
1
(m,⌊
N
A
2
⌋) (12)
where ⌊x⌋ is the integer part of x. Defined in this way
the asymmetry pattern accounts for approximately
half the possible rotations. This is because the re-
maining ones would only generate repeated values (as
A
1
(m,a) is an even function with respect to a):
∀a ∈ [1;N
A
] : A
1
(m,a) = A
1
(m,−a) (13)
where both addition and substraction are modulo N
A
operations. Then it follows that:
∀a ∈ [1;N
A
] : A
1
(m,a) = A
1
(m,N
A
− a) (14)
Intuitively, this can be understood from the defi-
nition as an overlap between m and a rotated version
of itself by an angle φ that we can call m
′
= R(m,φ).
The overlap between the two would be the same if we
rotate both m and m
′
by any angle, for example −φ,
which would transform shape m into R(m,2π − φ)
and shape m
′
into m. Hence, the overlap between
m and R(m,φ) is equivalent to the overlap between
m and R(m,2π − φ) and the same applies to both the
symmetry and asymmetry measures defined above.
2.4 Spatial Relationships
So far we have worked with a sequence m defined
as in (6), namely the bins of a ring at fixed elevation
and radius from the spherical support of a 3DSC. This
choice seems natural as it allows to transform each
(i-k) ring of a 3DSC descriptor x into an asymmetry
pattern that is invariant to the choice of azimuth.
Azimuth
Elevation
Figure 2: The World map as an example of a shell with (ide-
ally) constant radius. The azimuth (longitude) and elevation
(latitude) bins are also indicated.
Azimuth
Elevation
Figure 3: The same spherical shell as in Figure 2 after ar-
bitrary and independent azimuth rotations of two rings with
constant elevation (4-th and 8-th bins).
However, such a choice only takes into account
the spatial relationships within each (i-k) ring. To il-
lustrate this suppose that we consider all bins of x at
a fixed radius. This is a spherical shell and we could
represent it on a Cartesian plane similarly to a World
map, as the one shown in Figure 2, where the latitude
is the elevation and the longitud is the azimuth. If
we consider the representation of each ring indepen-
dently, then any azimuth shift of a ring has no effect in
our representation and both the correct World map of
Figure 2 and the example with shifted rings in Figure
3 will generate the same set of patterns. A similar rea-
soning can be applied to the relation between shells of
different radii. In contrast, when shifted versions of x
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
10

are generated to select the best match for 3DSC as in
equation (4), the whole sphere rotates at once and all
spatial relations are kept.
The above is not necessarily bad and, as we will
show, sometimes it might be useful to disable certain
spatial relationships. However, in the general case this
can lead to a loss of discriminant information.
The choice of what spatial relations are considered
is related to the definition of m. It is easy to verify
that each of the generated sequences must cover all
azimuth bins, as otherwise we would lose the invari-
ance of the patterns to azimuth rotations, but there is
no restriction regarding the variation of elevation and
radius within the sequence. In other words, equation
(6) is just a specific choice of m that leads to one of
many possible APSC. A few straightforward alterna-
tives include:
• Considering diagonals
1
, where the variation of
azimuth is accompanied by a variation in eleva-
tion and/or radius:
m
j
= x
i+ j, j,k
(15)
m
j
= x
i+ j, j,k+ j
(16)
• Jointly considering two (or more) rings that are
neighbors:
m
1, j
= x
i, j,k
, m
2, j
= x
i+1, j,k
A
2
(m,a) =
∑
j
|m
1, j
− m
1, j+a
| + |m
2, j
− m
2, j+a
|
(17)
Notice that, when jointly considering two or more
rings, the overlap is computed only between rings
with the same definition. All additions are circular,
modulo the corresponding number of bins (N
E
, N
A
and N
R
respectively for i, j and k).
In principle, the definition of the sequences can be
arbitrary and the aboveare just a few intuitivechoices.
Thus, APSC can be though of as a family of descrip-
tors with a flexible definition that allows to adapt them
to highlight or disable specific spatial relationships.
We will discuss the advantages and limitations of this
fact in Section 4.
3 EXPERIMENTAL EVALUATION
In this section we compare the performance of Asym-
metry Patterns Shape Contexts to the following three
algorithms, that constitute competing alternatives:
1
Given that the support region is spherical the resulting
sampling pattern is not a diagonal but we use this name in
analogy to the shape it would take if the bins were repre-
sented in a Cartesian grid.
• 3D shape contexts (3DSC) (Frome et al., 2004),
which generate descriptors that are not invariant
to azimuth rotations.
• Harmonic Shape Contexts (HSC) (Frome et al.,
2004), which achieve invariance to azimuth rota-
tions by decomposing each spherical shell at fixed
radius r
k
of a 3DSC descriptor into Spherical Har-
monics keeping only the modulus of the resulting
coefficients.
• Unique Shape Contexts (USC) (Tombari et al.,
2010), which compute a 3DSC with a unique ori-
entation of the spherical support region based on
the principal axes in a neighborhood of the inter-
est point and a sign disambiguation step.
In all cases we used the default configuration as
indicated in the original papers: N
E
= 11 elevation
bins, N
A
= 12 azimuth bins and N
R
= 15 radial bins.
The radius of the spherical support region was set to
r
N
= 30 mm and the minimum radius to r
min
= 1 mm
(see (1)). Spherical Harmonics were computed up to
order N
SH
= 16. Thus, 3DSC and USC had a total of
N
E
× N
A
× N
R
= 1980 bins while HSC had a total of
N
R
× N
SH
× (N
SH
+ 1)/2 = 2040 bins.
Regarding APSC, as mentioned before they can be
considered a family of descriptors with many possible
instances depending on the spatial relations selected
to construct the sequences m from which the asym-
metry patterns are derived. We performed tests using
the fixed elevation and radius rings (azimuth rings, for
short) as defined in (6) and eight other simple patterns
resulting from the diagonals (i.e. jointly changing the
bin indexes of azimuth with radius and/or elevation),
adjacent rings (either in elevation or radius) and com-
binations of diagonals and azimuth rings. From these,
we selected 5 representativecases to report, for which
we provide the corresponding equations in Table 1.
Results for the remaining four are available on-line
2
.
All sequences in Table 1 are computed starting
from a 3DSC descriptor x, whose elements are in-
dexed by (i, j,k) = (elevation, azimuth, radius). We
always generate sequences for all possible combina-
tions of i and k (while varying j), which results in a
full coverage of the bins of x. In the case of two se-
quences considered jointly (bottom three rows of the
table), they are combined to generate the asymmetry
pattern as indicated in (18). For each sequence, which
has always N
A
= 12 bins, an asymmetry pattern of
length ⌊
N
A
2
⌋ = 6 is generated. Thus, each APSC de-
scriptor has only N
E
× N
A
× ⌊
N
A
2
⌋ = 990 bins.
2
http://fsukno.atspace.eu/Research.htm
RotationallyInvariant3DShapeContextsusingAsymmetryPatterns
11

Table 1: Description of some specific spatial patterns for APSC descriptors. In all cases the sequences are generated by
varying the azimuth index j.
Abbreviation Sequence(s) equation Description
D
AR
m
j
= x
i, j,k+ j
Azimuth-Radius diagonal
D
AER
m
j
= x
i+ j, j, k+ j
Azimuth-Elevation-Radius diagonal
A+E m
1, j
= x
i, j,k
, m
2, j
= x
i+1, j,k
Azimuth ring + Elevation neighbors
A+R m
1, j
= x
i, j,k
, m
2, j
= x
i, j,k+1
Azimuth ring + Radial neighbors
A+D
AER
m
1, j
= x
i, j,k
, m
2, j
= x
i+ j, j, k+ j
Azimuth ring + Azim-Elev-Rad diagonal
3.1 Data
We frame our evaluation in the task of craniofacial
landmark localization. This landmark-based evalu-
ation has two important advantages with respect to
evaluations based on keypoints (i.e. points that are
considered highly discriminant or salient from the
point of view of a descriptor): i) all descriptors are
evaluated in the same set of points which are not nec-
essarily salient and, as in the case of facial landmarks,
can include diverse (local) geometries that pose dif-
ferent degrees of challenge to the descriptor; ii) the
evaluation is done on real world examples (e.g. a pop-
ulation of faces where anatomical correspondences
have been manually annotated) instead of using syn-
thesized examples obtained by modifying a given ex-
ample by some set of transformations (Tombari et al.,
2010; Bronstein et al., 2010; Steder et al., 2011).
Our test dataset consisted of 144 facial scans
acquired by means of a hand-held laser scanner
(FastSCAN
TM
, Colchester, VT, USA). Special care
was taken to avoid occlusions due to facial hair. The
extracted surfaces were subsampled by a factor of
4 : 1, resulting in an average of approximately 21.3
thousand vertices per mesh. The dataset contains ex-
clusively healthy volunteers who acted as controls in
the context of craniofacial dysmorphology research.
Each scan was annotated with a set of anatomical
landmarks, in accordance with definitions in (Hen-
nessy et al., 2002) (based on (Farkas, 1994)), from
which we target the 22 points indicated in Figure 4.
The fact that the test dataset was acquired in the
context of clinical research makes it especially suited
for tests in localization accuracy. As it can be ob-
served in Figure 4 these are high quality scans, which
have been carefully annotated by experts based on an-
thropometric definitions. Recent studies on manual
identification of 3D facial landmarks indicate that the
intra- and inter-observer uncertainty of this type of
annotations are typically between 1 mm and 2 mm
(Aynechi et al., 2011; Toma et al., 2009).
Figure 4: Example of the facial scans from the test dataset
with the annotation of the 22 landmarks used in this study:
en = endocanthion; ex = exocanthion; n = nasion; a =
alare; ac = alar crest; nt = nostril top; prn = pronasale; sn
= subnasale; ch = cheilion; cph = crista philtrum; li =
labiale inferius; ls = labiale superius; sto = stomion; sl =
sublabiale; pg = pogonion; (Hennessy et al., 2002).
3.2 Accuracy Discriminated by
Landmark
In this section we evaluate the performance of each
descriptor for the different landmarks on an individ-
ual basis. This is done using the expected local ac-
curacy e
L
(r
S
) defined by (Sukno et al., 2012). For
each descriptor and landmark that is targeted, e
L
(r
S
)
is computed as follows:
1. Start from an annotated set of shapes, in this case
facial surfaces represented by meshes M
i
.
2. For every vertex v ∈ M
i
compute a descriptor
score, s(v), which measures how similar is the de-
scriptor of vertex v to that of the landmark being
targeted.
3. For every vertex v ∈ M
i
compute also the Eu-
clidean distance to the correct position of the tar-
geted landmark, say d(v).
4. For each M
i
consider a neighborhood of radius r
S
around the ground truth position of the targeted
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
12

Table 2: Expected local accuracy [mm] for the different descriptors and landmarks. If a plateau is found, its value and limits
are indicated, otherwise (n.p - no plateau) is indicated. For each landmark (rows), the best descriptor is highlighted in boldface
as well as the ones with no statistically significant difference to it. The latter are further highlighted with an asterisk.
Lmk HSC USC 3DSC
APSC
D
AR
D
AER
A+E A+R A+D
AER
en 1.3* 1.9 1.4 1.5 1.5 1.4* 1.3 1.3*
(2) (2 - 24) (3 - 25) (3 - 25) (3 - 25) (3 - 25) (3 - 24) (3 - 25) (3 - 25)
ex 4.5
n.p
4.3 2.9 3.9 5.4 4.7 3.1*
(2) (16 - 90) (13 - 88) (6 - 67) (19 - 48) (13 - 88) (14 - 89) (8 - 88)
n
1.8 4.6 1.5 1.6* 1.6* 2.3 2.0 1.7*
(3 - 200) (5 - 12) (3 - 200) (4 - 200) (4 - 64) (4 - 200) (3 - 200) (4 - 200)
a 1.4*
n.p
1.4 2.9
n.p
2.1 1.8 2.0
(2) (3 - 26) (4 - 27) (6 - 12) (4 - 25) (4 - 26) (6 - 26)
ac 2.1* 5.8 4.7 9.0
n.p
2.3 2.1 5.1
(2) (5 - 25) (14 - 25) (9 - 25) (16 - 24) (7 - 25) (4 - 11) (14 - 25)
nt 2.0 12.2 8.0 6.9 7.5 2.3 2.2 6.6
(2) (4 - 8) (14 - 200) (14 - 200) (12 - 200) (11 - 200) (5 - 8) (5 - 9) (11 - 200)
prn
1.4 1.4 1.2 1.3 1.3* 1.3* 1.3* 1.3
(3 - 200) (2 - 200) (2 - 200) (3 - 200) (2 - 200) (2 - 200) (2 - 200) (3 - 200)
sn
1.8
n.p
1.6 1.8* 2.0 1.9 1.9 1.9
(4 - 200) (4 - 55) (4 - 22) (5 - 16) (3 - 200) (3 - 200) (4 - 200)
ch 3.8 2.4 2.1 2.5 2.9 2.8 2.9 2.3*
(2) (11 - 22) (4 - 42) (5 - 19) (9 - 29) (10 - 39) (6 - 18) (5 - 20) (5 - 28)
cph 2.1 13.3 8.4 7.1 7.0
n.p
7.7 2.7
(2) (4 - 9) (20 - 34) (18 - 200) (17 - 86) (16 - 59) (16 - 200) (5 - 8)
li
5.0 2.7 2.3 4.4 3.4 4.9 4.8 3.8
(16 - 51) (7 - 48) (5 - 10) (16 - 37) (11 - 45) (10 - 15) (9 - 15) (15 - 95)
ls
4.1
n.p
2.3* 2.7 2.2 5.2 5.7 3.8
(6 - 14) (8 - 46) (8 - 13) (6 - 11) (14 - 200) (10 - 54) (7 - 200)
sto
2.7* 2.9 2.2 2.5* 6.1 4.0 4.5 3.1
(6 - 14) (8 - 46) (8 - 78) (7 - 17) (14 - 40) (9 - 14) (11 - 89) (12 - 54)
sl
5.4 3.0 3.2* 5.5 7.4 4.7 6.0 6.2
(10 - 54) (10 - 18) (11 - 27) (13 - 79) (16 - 29) (11 - 77) (12 - 84) (17 - 62)
pg
7.0 11.6 5.4 7.9 7.1 7.6 5.6* 5.7*
(10 - 200) (19 - 120) (10 - 200) (19 - 200) (13 - 200) (13 - 26) (13 - 23) (10 - 200)
landmark and select v
max
i
as the vertex with the
maximum score in this neighborhood. Its distance
to the ground truth is d(v
max
i
).
5. There is one value of d(v
max
i
) for each mesh;
e
L
(r
S
) is their expected value over the test set:
e
L
(r
S
) = E[d(v
max
i,r
S
)] (18)
v
max
i,r
S
= {v ∈ M
i
|d(v) ≤ r
S
∧ ∀w 6= v,
d(w) ≤ r
S
,w ∈ M
i
: s(v) ≥ s(w)} (19)
where E[x] is the expected value of x. That is, given
a target landmark, for each mesh M
i
we consider a
neighborhood of radius r
S
around the ground truth
position of the landmark and select v
max
i
as the ver-
tex with the maximum score in this neighborhood.
We are interested in the expected distance of these
maximum-score vertices to the targeted landmark.
We used the negative Euclidean distance to a tem-
plate as the descriptor score. The template for each
landmark was computed as the median of descriptors
over a training set. The training and test sets were
obtained from the set of 144 facial scans described
above by means of 6 fold cross validation.
An indicative example is provided in Figure 5,
showing the obtained curves of e
L
(r
S
) for the nose
corner using USC, 3DSC and APSC (computing pat-
terns over A+E rings). The three curves show an ini-
tial growth of the error with the search radius until
they reach a nearly flat region or plateau. This is the
most important part of the curve because it provides
both the accuracy and usable local range of the de-
scriptor for the analyzed landmark. In other words,
for search radii at which e
L
(r
S
) is flat the descriptor
shows a stable behavior.
Hence, the first plateau is identified as the main
RotationallyInvariant3DShapeContextsusingAsymmetryPatterns
13

0 5 10 15 20 25 30 35 40 45 50
10
0
10
1
Search radius [mm]
Average Local Accuracy [mm]
USC
3DSC
APSC (A+E)
Figure 5: Average accuracy curves of USC, 3DSC and
APSC (computing patterns over A+ E rings) targeting the
nose corners (ac). Error bars indicate a 95% confidence in-
terval.
feature of the local accuracy curves, allowing to char-
acterize them with just three numbers: the value of
e
L
(r
S
) at the plateau and the plateau limits, in terms
of r
S
(Sukno et al., 2012). Table 2 summarizes the
results for all descriptors and landmarks.
Continuing with the example from Figure 5, it is
interesting to analyze the behavior of e
L
(r
S
) for radii
beyond the plateau: for the three descriptors in the
plot there is a sudden increase of the error at radii be-
tween 25 and 30 mm. Typically this obeys to the pres-
ence of a strong source of false positives (i.e. points
with very high score but not too close to the target
landmark) at the distance where the error increase is
observed. In this case, the source of false positives
is the bilaterally symmetric point (i.e. the other nose
corner), which is indeed typically located at 25 to 30
mm. This explains the strong coincidence in the up-
per plateau limits shown in Table 2 for nose corners
(ac) or the inner eye-corners (en), as the bilaterally
symmetric points are relatively close to each other.
The sources of false positives are not necessarily
the symmetric point to the one targeted and depend on
the descriptor that is used. There are also two special
types of points: i) the ones without false positives in
the analyzed range (which we set to 200 mm for the
human face); ii) points that do not show a stable be-
havior in terms of e
L
(r
S
), which are indicated in Table
2 by n.p (no plateau).
From the results in Table 2 we can conclude that:
• For the majority of landmarks, at least one of the
specific patterns of APSC that we tested showed
comparable performance to the best descriptor.
• For eight landmarks (ex(2), ac(2), nt(2) and
cph(2)) there were one or more APSC descrip-
tors that significantly outperformed 3DSC. Inter-
estingly, HSC also outperformed 3DSC for ac, nt
and cph, but not for ex.
• There were four landmarks (a(2), li and sl) for
which none of the tested APSC achieved sufficient
performance when compared to 3DSC.
• The performance of APSC descriptors depend-
ing strongly on the spatial patterns that are con-
sidered. Jointly considering two rings produced
lower errors than APSC derived from single rings.
3.3 Overall Accuracy
While the description of local accuracy curves based
on the first plateau allows to simplify the comparison
on a per-landmark basis, inferring the overall perfor-
mance of a descriptor from Table 2 is not straightfor-
ward as the radii of the plateaus vary considerably for
each landmark and descriptor.
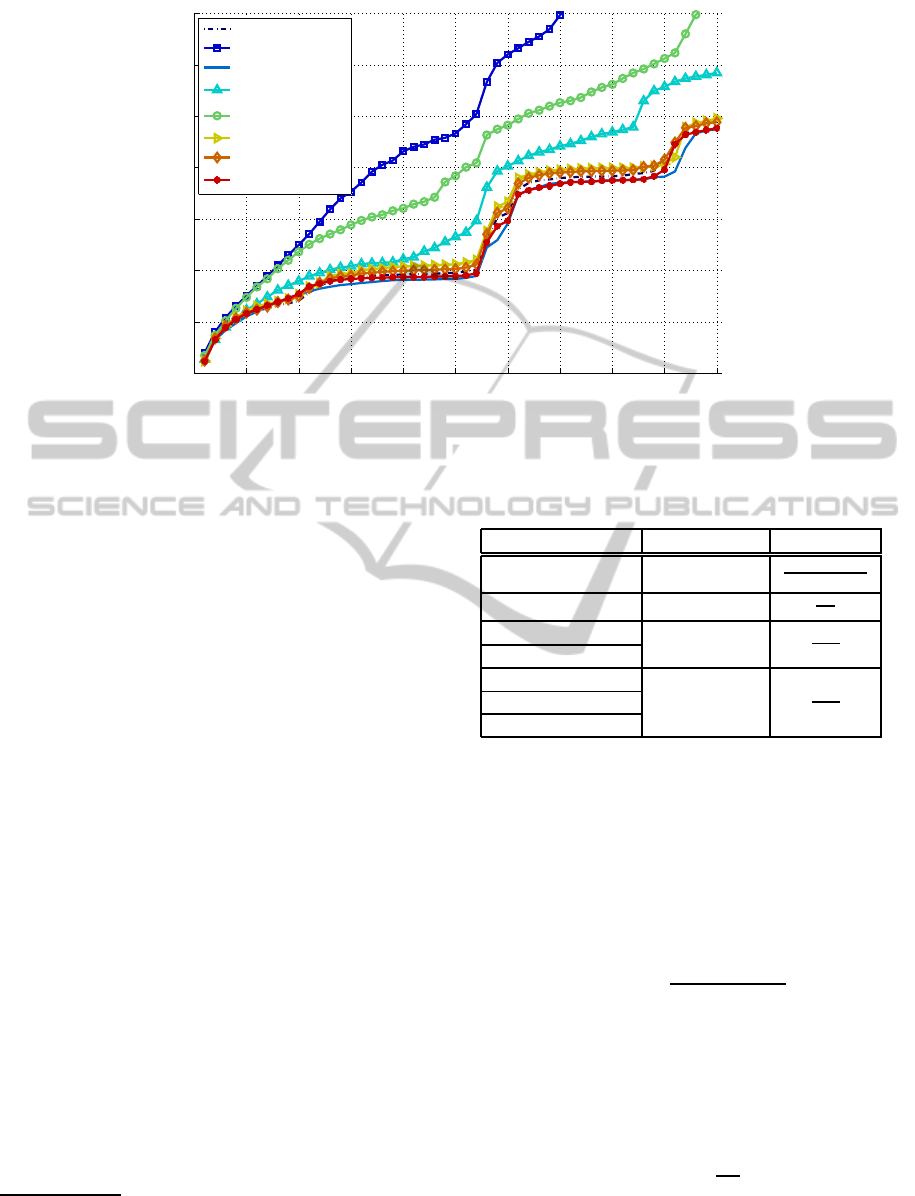
Hence, in Figure 6 we provide curves of e
L
(r
S
)
averaged over all 22 landmarks for each descriptor.
Observe that 3DSC, HSC and the three APSC using
patterns of two rings (A+E, A+R and A+D
AER
) show
very similar overall accuracy. Although we do not
show error bars (to keep the plot as clear as possible),
it is evident that the differences between these five de-
scriptors are not statistically significant. On the other
hand, USC and the two APSC based on a single ring
(D
AE
and D
AER
) showed poorer performance.
Therefore, the plots in Figure 6 confirm that, in
general, considering individual rings (either at con-
stant radius and elevation or in diagonal form) implies
a loss of important information, as all spatial relation-
ships between different rings are not taken into ac-
count (Section 2.4). Nevertheless, Table 2 shows that
for some particular cases this might not have an im-
pact in local accuracy (e.g. nasion, pronasale, labiale
superius) or might even be beneficial (exocanthion).
3.4 Implementation and Complexity
Our implementations of 3DSC and USC are based on
the Point Cloud Library (Rusu and Cousins, 2011)
with some modifications to improve the computa-
tion speed by removing redundant operations and in-
cluding multi-threading with OpenMP (Dagum and
Menon, 1998). Additionally, a trilinear interpolation
was included in the construction of the histograms as
it was experimentally found to improve the perfor-
mance of all tested descriptors.
It is interesting to analyze the sign disambigua-
tion step when deriving the axes for USC: the ori-
entations of the generated normals
3
were not consis-
tently pointing inwards or outwards for 30% to 35%
3
As indicated in (Tombari et al., 2010) none of the ref-
erence axes derived for USC actually coincide with the true
normal as the contribution of each point to the covariance
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
14
0 5 10 15 20 25 30 35 40 45 50
0
2
4
6
8
10
12
14
Search radius [mm]
Average Local Accuracy [mm]
HSC
USC
3DSC
APSC (D
AR
)
APSC (D
AER
)
APSC (A+E)
APSC (A+R)
APSC (A+D
AER
)
Figure 6: Average accuracy curves of all tested descriptors considering all landmarks together (by averaging).
of points. This is easy to verify and correct in our
case as the input data are facial surfaces. The results
reported in this paper include the correction of the
reference frame orientation to ensure that all normals
were pointing outwards of the object, which reduced
the overall error of USC by approximately 10%. The
latter suggests that similar inconsistencies might also
exist in the sign of the other axes (and hence in the
origin of the azimuth bins), which explains the lower
accuracy of USC with respect to the other methods
that were tested.
Regarding the computational complexity, there
are two different aspects to consider: i) the compu-
tation of the descriptor and ii) the point-wise compar-
isons or matching.
The fastest descriptor to compute is 3DSC, as all
the others are built from it plus some additional step.
In the case of USC the additional step is dominated
by an SVD on a neighborhood of the point of interest.
For APSC and HSC the additional step is carried out
based on the 3DSC bins and is therefore decoupled
from the sampling density of the mesh. However, the
computation of the histogram to build the 3DSC de-
scriptor depends on the number of neighbors consid-
ered and, therefore, on the density of the mesh.
The above hampers for an exact analysis of com-
plexity. Thus, in Table 3 we provide numerical results
for the computation time of the descriptors, in rela-
tive terms to the computation time of 3DSC, which
in our experiments averaged 3.45 seconds on an In-
tel Xeon E5320 @1.86 GHz. Note that HSC was
matrix is weighted by the distance to the interest point.
Nonetheless, this deviation with respect to the true normal
is much smaller than the 180 degrees of a sign flip.
Table 3: Computational complexity of the descriptors rela-
tive to 3DSC.
Descriptor Computation Matching
HSC 11.1
N
SH
(N
SH
+1)
2N
E
N
2
A
USC 1.23
1
N
A
APSC (D
AR
)
1.05
1
2N
A
APSC (D
AER
)
APSC (A+E)
1.09
1
2N
A
APSC (A+R)
APSC (A+D
AER
)
approximately an order of magnitude slower than all
other descriptors as it required the decomposition of
each fixed-radius shell into Spherical Harmonics. As-
suming that the N
SH
×(N
SH
+1)/2 basis functionsare
pre-computed, we still need to perform the projection
into each of them of every shell, which roughly im-
plies N
A
× N
E
complex multiplications and additions.
Thus, the whole decomposition takes at least:
O
N
A
N
E
N
R
N
SH
(N
SH
+ 1)
2
(20)
The above cost is considerably higher than the
cost of computing APSC, which for each ring m takes
only O(N
2
A
/2) additions. Thus, if considering only
single rings, the total complexity added by APSC to
the computation of 3DSC is:
O
N
A
N
E
N
R
N
A
2
(21)
This cost grows linearly with the number of rings
jointly considered, so it doubles for the last three rows
RotationallyInvariant3DShapeContextsusingAsymmetryPatterns
15

of Table 3. Note that the complexities in (21) and
(22) are not directly comparable as the first one is a
lower bound based on complex additions and multi-
plications while the latter involvesonly real additions.
The matching time depends exclusively on the
bins for all descriptors. Hence, the relative complex-
ity to that of 3DSC can be easily derived and is shown
in Table 3. Being the fastest to compute, 3DSC are
also the slowest to match as they require to compute
the N
A
distances that correspond to all possible az-
imuth rotations, as in equation (4). All other descrip-
tors are azimuth invariant and hence compute a single
distance. In the case of HSC, as the number of bins is
different to 3DSC, the relative computation time de-
pends on the choice of N
SH
, but approaches (1/N
A
)
with the default parameters. Finally, all APSC have
just half as many bins as 3DSC and USC which makes
them the fastest to match.
4 DISCUSSION
From the results presented in the previous section we
can conclude that APSC allows to construct descrip-
tors that perform comparably to 3DSC, in terms of
overall accuracy, with little extra load in the computa-
tion of the descriptor (< 10% in our experiments) and
run several times faster during matching.
With respect to the previousalternativesto achieve
azimuth-invariance in shape contexts, APSC showed
similar accuracy to HSC at a much lower computa-
tional load (an order of magnitude) and outperformed
USC both in terms of accuracy and speed.
However, the greatest potential of APSC is their
flexibility to derive different descriptors depending on
the spatial patterns that are selected to construct the
sequences m, from which asymmetry is extracted. As
shown in Table 2, specific choices of spatial patterns
might produce considerably lower errors than those
obtained with 3DSC for certain landmarks.
The spatial patterns that were tested correspond
to some straightforward definitions from a large set
of possibilities. While the wrong choice of spatial
patterns might negatively affect the performance, it
would be expected that more elaborated strategies to
choose these patterns, such as feature selection, would
bring further improvement. While feature selection
strategies would also be possible in 3DSC, the issue of
azimuth ambiguity can considerably complicate the
search of an optimal solution.
It might be argued that none of the tested APSC
was optimal for all landmarks and a potential reduc-
tion of the error generalized through the majority of
points would require different APSC to targeted dif-
ferent landmarks. Nonetheless such a strategy is pos-
sible and is analogous to previous works in land-
mark localization that adopt different features to lo-
calize each facial landmark (Gupta et al., 2010; Se-
gundo et al., 2010). Moreover, combining two or
more APSC can be far more efficient than combining
other different descriptors, as the extra computation
required would be rather marginal (all spatial patterns
are extracted from the same 3DSC, which would be
computed only once). For example, from Table 3 we
see that all five APSC descriptors tested in this paper
can be computed together with less than 1.4 times the
computational load of a single 3DSC descriptor.
5 CONCLUSIONS
In this paper we present a new family of 3D geo-
metric descriptors, Asymmetry Patterns Shape Con-
texts (APSC). These descriptors provide invariance to
azimuth rotations to the popular 3D Shape Contexts
(3DSC) by adapting a simple measure of rotational
symmetry that has been recently proposed based on
the overlap of a shape with rotated version of itself.
The asymmetry patterns are computed from se-
quences of bins extracted from a 3DSC descriptor by
varying the azimuth index and, optionally, the radial
and/or elevation bins. This allows to define differ-
ent APSC descriptors to highlight or disable some of
the spatial patterns present in the spherical grid of a
3DSC, which can be used to specialize the descriptor
for different types of points.
We evaluated five examples of APSC in terms of
local accuracy by targeting 22 craniofacial landmarks
on a set of 144 facial scans. The accuracy was mea-
sured in terms of distance to ground truth consisting
of expert annotations. Our results showed that APSC
can achieve comparable overall accuracy to 3DSC,
providing invariance to azimuth rotations at the ex-
pense of a small overhead in the computation of the
descriptor, which did not exceed 10%. On the other
hand the rotation invariance reduces the time required
for matching two descriptors by twice the number of
azimuth bins. APSC were also showed to perform
better than previous approachesthat provided azimuth
invariance to shape contexts.
ACKNOWLEDGEMENTS
The authors would like to thank their colleagues in
the Face3D Consortium (www.face3d.ac.uk), and the
financial support provided from the Wellcome Trust
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
16

(grant 086901/Z/08/Z) and the Marie Curie IEF pro-
gramme (grant 299605, SP-MORPH).
REFERENCES
Aynechi, N., Larson, B., Leon-Salazar, V., et al. (2011). Ac-
curacy and precision of a 3D anthropometric facial
analysis with and without landmark labeling before
image acquisition. Angle Orthod, 81(2):245–252.
Bariya, P., Novatnack, J., Schwartz, G., et al. (2012). 3D
geometric scale variability in range images: features
and descriptors. Int J Comput Vis, 99(2):232–255.
Bronstein, A., Bronstein, M., Castellani, U., et al. (2010).
SHREC 2010: robust correspondence benchmark. In
Eurographics Workshop on 3D Object Retrieval.
Chen, H. and Bhanu, B. (2007). 3D free-form object recog-
nition in range images using local surface patches.
Pattern Recogn Lett, 28(10):1252–1262.
Creusot, C., Pears, N., and Austin, J. (2011). Automatic
keypoint detection on 3D faces using a dictionary of
local shapes. In Proc. 3DIMPVT, pages 204–211.
Dagum, L. and Menon, R. (1998). OpenMP: an industry
standard API for shared-memory programming. IEEE
Computat Sci Eng, 5(1):46–55.
Farkas, L. (1994). Anthropometry of the head and face.
Raven Press (New York), 2nd ed.
Frome, A., Huber, D., Kolluri, R., et al. (2004). Recogniz-
ing objects in range data using regional point descrip-
tors. In Proc. ECCV, pages 224–237.
Guo, Q., Guo, F., and Shao, J. (2010). Irregular shape
symmetry analysis: Theory and application to quan-
titative galaxy classification. IEEE T Pattern Anal,
32(10):1730–1743.
Gupta, S., Markey, M., and Bovik, A. (2010). Antopometric
3D face recognition. Int J Comput Vis, 90(3):331–349.
Hennessy, R., Kinsella, A., and Waddington, J. (2002).
3D laser surface scanning and geometric morpho-
metric analysis of craniofacial shape as an index of
cerebro-craniofacial morphogenesis. Biol Psychiat,
51(6):507–514.
Johnson, A. and Hebert, M. (1999). Using spin images
for efficient object recognition in cluttered 3D scenes.
IEEE T Pattern Anal, 21(5):433–449.
Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2004).
Symmetry descriptors and 3D shape matching. In Eu-
rograph. Symp. on Geometry process, pages 115–123.
Kortgen, M., Park, G., Novotni, M., et al. (2003). 3D shape
matching with 3D shape contexts. In Central Europ
Seminar on Comput Graph.
Passalis, G., Perakis, N., Theoharis, T., et al. (2011). Us-
ing facial symmetry to handle pose variations in real-
world 3D face recognition. IEEE T Pattern Anal,
33(10):1938–1951.
Rusu, R., Blodow, N., and Beetz, M. (2009). Fast point fea-
ture histograms (FPFH) for 3D registration. In Proc.
ICRA, pages 3212–3217.
Rusu, R. and Cousins, S. (2011). 3D is here: Point cloud
library (PCL). In Proc. ICRA, pages 1–4,
Segundo, M., Silva, L., Bellon, O. P., et al. (2010). Auto-
matic face segmentation and facial landmark detection
in range images. IEEE T Syst Man Cy B, 40(5):1319–
1330.
Steder, B., Rusu, R., Konolige, K., et al. (2011). Point fea-
ture extraction on 3D range scans taking into account
object boundaries. In Proc. ICRA, pages 2601–2608.
Sukno, F., Waddington, J., and Whelan, P. (2012). Com-
paring 3D descriptors for local search of craniofacial
landmarks. In Proc. ISVC, pages 92–103.
Toma, A., Zhurov, A., Playle, R., et al. (2009). Re-
producibility of facial soft tissue landmarks on 3D
lasser-scanned facial images. Orthod Craniofac Res,
12(1):33–42.
Tombari, F., Salti, S., and Stefano, L. D. (2010). Unique
shape context for 3D data description. In Proc. ACM
Workshop on 3D object retrieval, pages 57–62.
Zaharescu, A., Boyer, E., and Horaud, R. (2012). Keypoints
and local descriptors of scalar functions on 2D mani-
folds. Int J Comput Vision, 99(2):232–255.
Zhang, Y. (2009). Intrinsic shape signatures: a shape de-
scriptor for 3D object recognition. In Proc. ICCV
Workshops, pages 689–696.
APPENDIX
Starting from the definition of A and S :
A (m,a) = 1− S (m,a) = 1 −
∑
j
min(m
j
,m
j+a
)
∑
j
m
j
=
∑
j
m
j
−
∑
j
min(m
j
,m
j+a
)
∑
j
m
j
(22)
Now we use the following equality:
2
∑
j
m
j
=
∑
j
max(m
j
,m
j+a
) + min(m
j
,m
j+a
)
(23)
which holds because for every pair (m
j
,m
j+a
) one el-
ement is the maximum and the other one the mini-
mum, hence adding both guarantees to include each
element of m exactly twice in the summation (recall
that j + a is an addition module the cardinality of m).
Then, in (23):
∑
j
m
j
−
∑
j
min(m
j
,m
j+a
) =
=
1
2
∑
j
max(m
j
,m
j+a
) − min(m
j
,m
j+a
)
=
1
2
∑
j
|m
j
− m
j+a
| (24)
which directly leads to our final result:
A (m,a) =
1
2
∑
j
|m
j
− m
j+a
|
∑
j
m
j
(25)
RotationallyInvariant3DShapeContextsusingAsymmetryPatterns
17
