Suitable Optical Filter for Self-phase Modulation Regenerators

Gábor Fekete and Eszter Udvary

Broadband Infocommunications and Electromagnetic Theory, Budapest University of Technology and Economics,

Egry József utca 18. H-1111, Budapest, Hungary

Keywords: 2R, Nonlinearity, Optical Filter, Optical Regenerator, Reshaping, SPM.

Abstract: In this paper a 2R all-optical regenerator will be presented, which based on the nonlinear self-phase

modulation. The regenerator was simulated with the VPI TransmissionMaker and its optical filter module

was examining, because the optical filter is the main element of these types of regenerators.

1 INTRODUCTION

Long haul optical networks need regenerators

because of fibre attenuation and the dispersions.

Signal reshaping can be performed in the electrical

or optical domain, although the 3R (re-amplifying,

reshaping, retiming) regenerator exists only in the

electrical domain. Nonlinear effects in the optical

networks are usually the source of signal distortion,

but they are the bases of the all-optical regenerators’

reshaping mechanism. A nonlinear device can be a

nonlinear fibre or a semiconductor optical amplifier

(SOA). In this paper a 2R optical regenerator will be

introduced which will use the nonlinear self-phase

modulation (SPM) effect for reshaping. The

regenerator was simulated with the VPI Photonics

TransmissionMaker 8.7 (VPI) software. Increased

attention was given to the optical filter, because its

price can be high if special needs arise or special

parameters are required.

2 NONLINEAR PHASE

MODULATION

There are two types of nonlinear phase modulation:

self-phase modulation (SPM) and cross-phase

modulation (XPM). In the first case the signal’s own

intensity causes an additional phase modulation on

the signal, while in the second case the phase

modulation is caused by another signal’s intensity.

Nonlinear phase-modulation is based on the optical

Kerr-effect. The refractive index of the fibre core

changes as light propagates through on it. The value

of this change can be calculated (Ferreira, 2011)

with equation (1), where n

is the nonlinear index of

the fibre and I is the intensity of the propagating

light. This refractive index change causes different

propagation velocity which results different

propagation times, so the signal’s phase will

different at every point of the fibre. It seems that not

only the signal’s intensity was modulated, but its

phase too. In fact it was modulated only in its

intensity. The phase change can be calculated

(Ferreira, 2011) with equation (2), where i is the

channel number index. The first term on the right of

(2) represents the phase change due to SPM, while

the second term is the change caused by XPM. The

created regenerator in VPI was based on the SPM

effect.

Inn







(1)





















 ji

)t(I2)t(I

Ln2







(2)

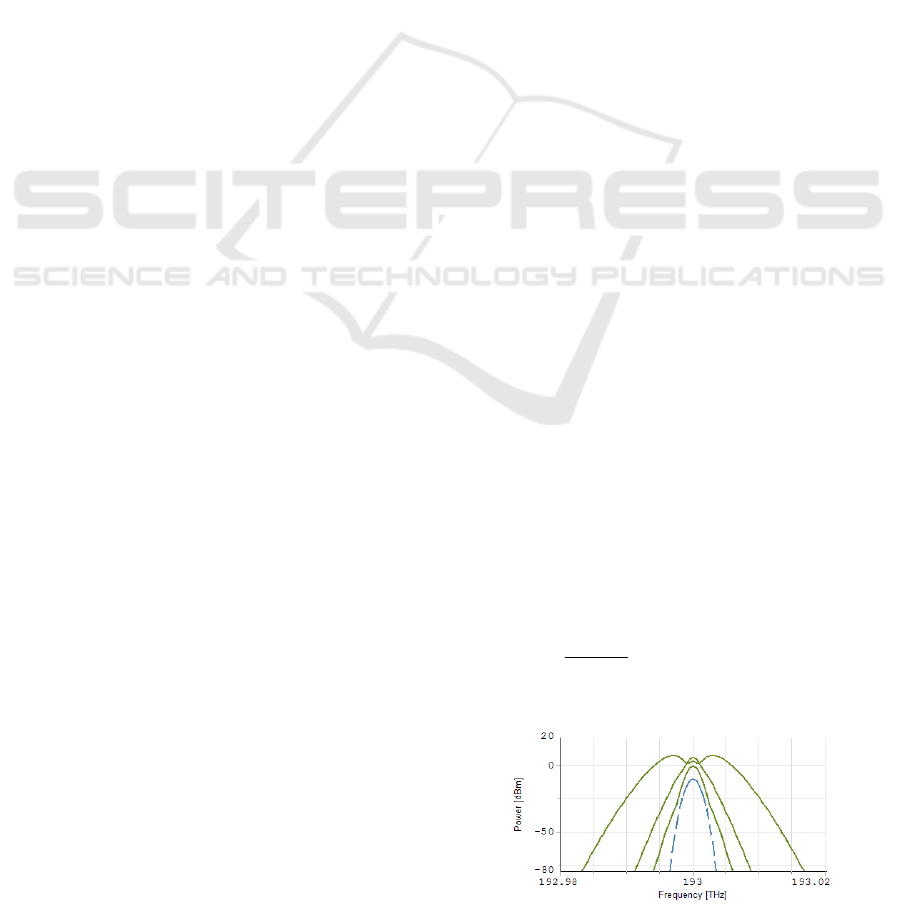
Figure 1: Spectral broadening caused by SPM. The blue

dash curve is a 2mW pulse’s spectrum without the effect

of SPM, while the green solid curves show the spectral

broadening effect on a 20, 100, 600mW (from inside to

outside) power pulse.

Fekete G. and Udvary E..

Suitable Optical Filter for Self-phase Modulation Regenerators.

DOI: 10.5220/0004275300680072

In Proceedings of the International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2013), pages 68-72

ISBN: 978-989-8565-44-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

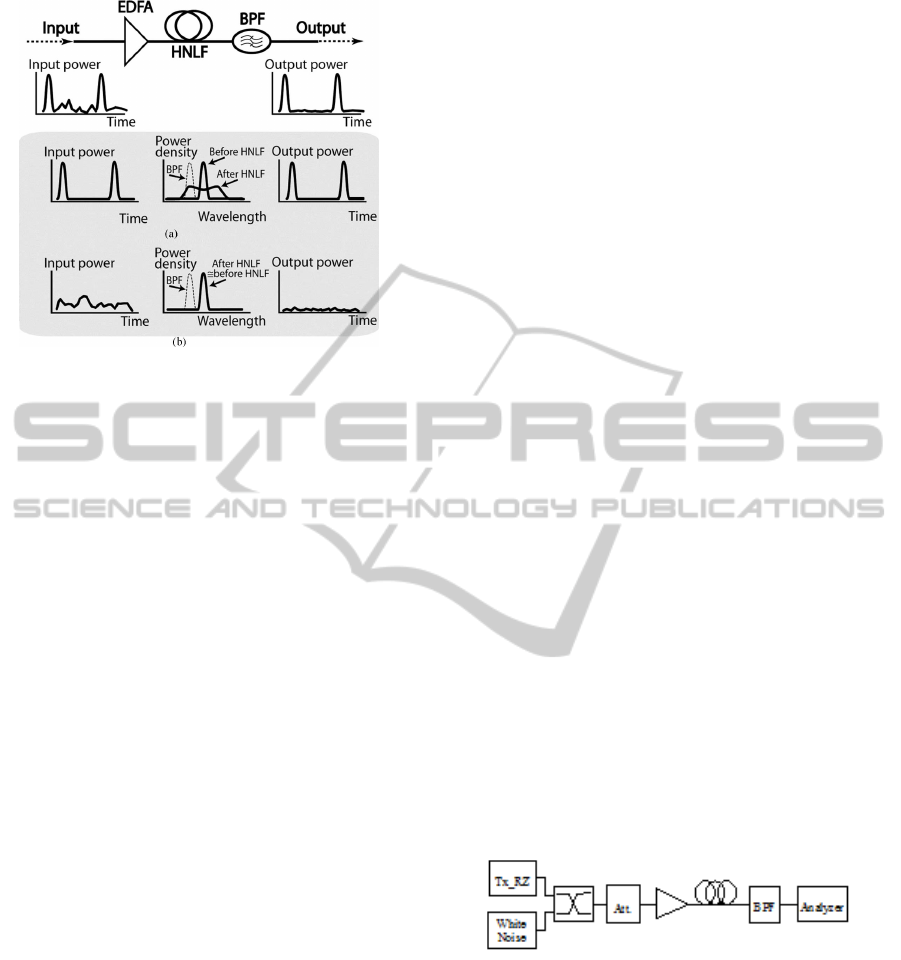
Figure 2: Block diagram of the simulated SPM

regenerator. (a) Signal and (b) noise are in the time and

frequency domain. (Rochette, Fu, Ta’eed, Moss and

Eggleton, 2006).

SPM does not change the pulse shape in the time

domain. It just causes spectrum broadening in the

frequency domain. Higher intensity causes bigger

spectral broadening as reported in Figure 1. It was

simulated with the VPI and the SPM effect was

produced by the regenerator’s nonlinear fibre

section. The blue dash curve shows the spectrum of

a pulse with 2mW power after the fibre. In this case

the fibre’s nonlinearity was turned off. Then it was

turned on, but the effect of SPM was negligible, so it

is not observable. The green curves show how the

signal’s spectrum broadening at higher pulse power

levels.

3 WORKING PRINCIPLE

SPM regenerators consist of three elements: an

amplifier, a fibre and an optical band pass filter

(Figure 2). Use of a highly nonlinear fibre is

recommended, because of the higher nonlinear effect

and it needs less power to reach its nonlinear

behaviour. The optical amplifier can be a commonly

used EDFA (Erbium Doped Fibre Amplifier) or a

SOA. It has to amplify the signal at least to a

minimum power level, which needs for the effect of

SPM to start taking place. If we reach or exceed that

power, the signal’s spectrum will be broadening by

the SPM. The regenerator’s principle of operation

(Mamyshev

, 1998) can be seen on Figure 2. The

pulse’s intensities are much higher than the noise

level and the pulses have coherent phase, while the

noise does not. Their spectrums’ shapes are very

similar, but completely different in the time domain.

The nonlinearity of the fibre will broaden the

signal’s spectrum, but the noise spectrum will not

broaden, because its power is too low for any

noticeable broadening, as we saw in Figure 1. One

piece of the broadened spectrum has to fall into the

optical band pass filter’s bandwidth, otherwise only

noise is at the output of the regenerator. The

regenerator works properly, if the whole noise’s

spectrum is filtered out by the filter. Its centre

frequency is shifted away a little bit due to the noise.

This can be critical in the DWDM (Dense

Wavelength Division Multiplexing) systems, where

the wavelength accuracy is important.

4 SIMULATIONS

The transmitter produces 2mW high RZ (return to

zero) pulses at 193.1THz with a bit rate of 0.5Gbps.

Its bit sequence was set to an alternating stream. The

signal degradation was simulated with a white noise

block and an attenuator. The white noise was added

to the signal with a coupler which introduced an

additional attenuation of 3dB. The noise was

considered Gaussian-distributed and its spectral

power density was 10

-16

W/Hz. The attenuator was

placed after the coupler. It created an overall loss of

10dB. In the regenerator a black box amplifier was

used, because only the amplifier’s gain was

important in our investigation, not the amplifying

technique. Its gain was 30dB and it also added noise

to the signal. A standard single mode fibre was used

instead of a highly nonlinear fibre, because its price

is much lower, but we had to use higher intensity for

the nonlinear effect to appear and a longer fibre

span.

Figure 3: Block scheme of the simulated regenerator.

These two disadvantages can easily eliminate the

price benefit of the standard fibre. In the simulation

the fibre’s length was 80km, which is four times

longer, than an average dispersion compensating

fibre’s length which is used in networks. An optical

filter was placed at the output of the regenerator and

an analyzer connected to its output to monitor the

signal (Figure 3). Three filter types were simulated,

which had different kind of transfer function. The

1GHz wide spectrum is broadened to 5.5GHz using

SuitableOpticalFilterforSelf-phaseModulationRegenerators

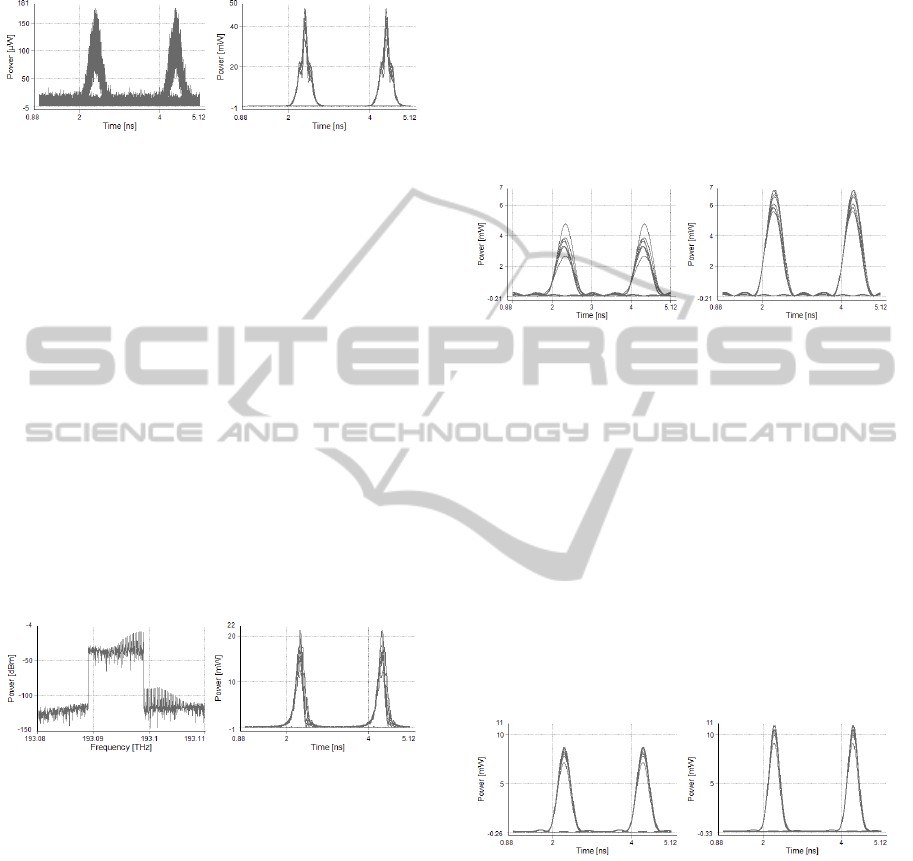
these settings. The width of the spectrum was

measured between the -3dB points.

Figure 4: (a) Nearly closed eye diagram at the regenerator

input. (b) Output eye diagram is distorted by nonlinearity

and noise.

4.1 Ideal (Rectangular) Filter

In the simulation the filter’s attenuation in the stop

band was 80dB. Because of its ideal feature it was

used for examine the filter roles and the required

filter’s bandwidth. The filter’s bandwidth was set to

10GHz and its centre frequency was equal to the

signal’s frequency. The regenerator with these

properties works as a simple amplifier. However the

fibre produces a strong nonlinearity because of the

input power level. It distorts the output signal. The

filter filters out those noise components, which are

out of the broadened signal’s spectrum. This can

improve the signal quality if the noise is out of the

signal band (Figure 4).

Figure 5: Spectrum and eye diagram at the filter’s output.

In the second case the filter centre frequency was

shifted by 6GHz to the 193.094THz, so that the

signal’s centre frequency was filtered out. The

filter’s other properties did not change. The result

can be seen on Figure 5. Half of the filtered signal is

part of the broadened signal and the other half of it is

the noise. The pulses fluctuated stronger and their

power decreased twofold compared to the previous

case (Figure 4). This simulation shows that the

filter’s pass band must contain only a part of the

broadened signal’s spectrum.

Final simulations with the rectangular filter were

carried out to find the optimal centre frequency and

bandwidth. One of the -3dB point was at

approximately 193.0972THz. This point and the

5.5GHz signal broadening rather limited our options.

There is no sense to use lower frequencies than the -

3dB point’s frequency because they are near to the

noise floor. The centre frequency of the filter was set

up to 193.097 and 193.098THz. The filter’s

bandwidth was 2GHz, because if it had been bigger,

we would have used the other half of the spectrum,

which contains the noise (Figure 2). The higher

centre frequency choice is better (Figure 6) because

of the higher output power. The fluctuations at the

high level are quite similar.

Figure 6: Eye diagrams at the output, when the filter’s

centre frequency was (a) 193.097THz and (b)

193.098THz. The bandwidths were same.

4.2 Trapezoid Filter

These filters are a better model to represent the real

filters because their slope is limited. In the

simulation the filter’s centre frequency was set to

193.098THz and its bandwidth was 2GHz. The

filter’s slope was 40 and 20dB/GHz. The eye

diagrams can be found in Figure 7. They are opened

eye and the fluctuations are approximately 1mW

high. When the filter’s slope was changed to

20dB/GHz the eye had a slightly larger fluctuation.

Figure 7: Eye diagrams after the filter when its slope was

(a) 40 and (b) 20dB/GHz.

4.3 Butterworth Filter

This is a real filter type, which has maximal flat

band pass. It has smaller slope between the pass

band and the stop band, than the trapezoid filter. Its

slope was about 5dB/GHz. The simulated filter was

second order filter and its centre frequency was also

set to 193.098THz with a bandwidth of 2GHz. The

spectrum at the regenerator’s output can be seen in

Figure 8. The eye diagram is opened, but it is

(a)

(b)

(a) (b)

PHOTOPTICS2013-InternationalConferenceonPhotonics,OpticsandLaserTechnology

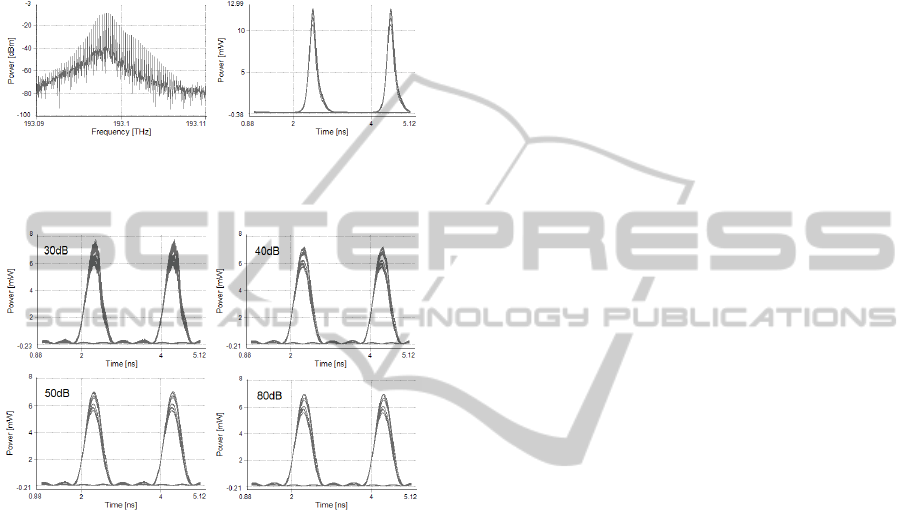
moderately asymmetric. It shows that the edges from

high level to low level have a little bit smaller slope

at the end than the low to high edges. This time the

fluctuation was 2mW at the high level. It exceeds

the previous case’s result by 1mW. This

considerable change results from the filter’s smaller

slope which causes worse noise spectrum filtering.

Figure 8: The output spectrum and the eye diagram when a

second order Butterworth filter was used.

Figure 9: Eye diagrams at the output of the regenerator at

different filter’s stop band attenuation.

4.4 Attenuation at the Stop Band

The stop band attenuation is one of the critical

aspects of the filters. If it is too low, the filter will

not be sufficiently attenuating the disturbing

components, so the output signal will be distorted. In

this simulation the minimum stop band attenuation

was examined. A rectangular filter was used with

2GHz bandwidth with a centre frequency of

193.098THz. The filter’s stop band attenuation was

changing from 30 to 80dB with 10dB increments.

The eye diagrams are shown in Figure 9. At 30 and

40dB attenuation the filter can no adequately

suppress the disturbing components, so the signal

has a fast fluctuation at the high levels. Beside this

fast fluctuation the output signal also shows slow

changes. The pulses differ from each other by a

small proportion. There are not any significant

changes in the eye diagrams from the 50dB stop

band attenuation. The pulses at the output differ

from the others, but this difference has a maximum

of 1mW. There are no fast changes on the high

levels. In conclusion the output filter has to have at

least 50dB attenuation at the stop band and it needs

to reach this value as fast as it possible.

5 CONCLUSIONS

We demonstrated with simulations the nonlinear

SPM effect and how it can be used in optical

regenerators. The simulation showed that a standard

fibre can be used instead of a highly nonlinear fibre.

Using a standard fibre the spectrum broadening will

be smaller or the signal’s power has to be higher at

the nonlinear device’s input to get the same

spectrum broadening. The regenerated signal’s

quality mainly depends on the filter. The signal

frequency must be shifted away to get right

regeneration. The signal regeneration depends on the

filter’s slope too. Higher filter’s slope gives better

signal reshaping as we showed. We also presented

that the signal’s shape do not improve if the stop

band attenuation of the filter is higher than 50dB.

All in all the applied filter’s pass band has to be out

of the range of the input noisy signal’s spectrum, but

inside of the broadened spectrum. That part of

broadened spectrum should be selected practically

where the signal’s power is maximal. The filter has

to attenuate 50dB out of the pass band and the slope

between the pass band and stop band has to be as

high as possible.

ACKNOWLEDGEMENTS

The authors acknowledge the Hungarian National

Research Foundation (OTKA) project No. CK

77997 and the Ericsson Hungary for funding their

research.

REFERENCES

Mário F. S. Ferreira, 2011. Nonlinear effects in optical

fibers, John Wiley & Sons, Inc., Hoboken, New Jersey

Masayuki Matsumoto, 2004. Performance Analysis and

Comparison of Optical 3R Regenerators Utilizing

Self-Phase Modulation in Fibers, IEEE.

Martin Rochette, Libin Fu, Vahid Ta’eed, David J. Moss,

Benjamin J. Eggleton, 2006. 2R Optical Regeneration:

An All-Optical Solution for BER Improvement, IEEE

P. V. Mamyshev, 1998. All-optical data regeneration

based on self-phase modulation effect, ECOC’98.

SuitableOpticalFilterforSelf-phaseModulationRegenerators

L. B. Fu, M. Rochette, V. G. Ta’eed, D. J. Moss, B. J.

Eggleton, 2005. Investigation of self-phase modulation

based optical regeneration in single mode As2Se3

chalcogenide glass fiber, OPTIC EXPRESS Vol. 13,

No.19.

T. Berceli and P. Herczfeld, 2010. Microwave Photonics—

A Historical Perspective, IEEE Trans. on Microwave

Theory and Techniques, Vol. 58, No.11, pp. 2992-

3000.

PHOTOPTICS2013-InternationalConferenceonPhotonics,OpticsandLaserTechnology