
On the Detection and Matching of Structures on Less-textured Scenes
Wan-Lei Zhao
1
, Wonmin Byeon
2
and Thomas M. Breuel
2
1
INRIA Rennes, Rennes Cedex, France
2
University of Kaiserslautern, Gottlieb-Daimler-Str, Kaiserslautern, Germany
Keywords:
Local Structure, Less-Textured Scene, Object Matching.
Abstract:
Due to the lack of non-zero gradients around the structures in the less textured scenes, current local feature
can hardly be applied in less textured object detection. To deal with this issue, two types of local structures,
namely, corner and closed region are proposed in this paper. They are based on purely object contours, which
are easier to obtain in less textured scenes. Compare to existing detectors, these features describe objects’
local structures in a better way. In addition, these new type of local structures also bring the advantage that
allows us to have different level of abstraction on the object structures. Its effectiveness has been evaluated
under various transformations.
1 INTRODUCTION
Keypoint features have been widely explored in the
last decade due to its unique advantages over global
features. They have been successfully applied in wide
range of applications and systems, such as wide base-
line matching (Matas et al., 2002), object retrieval and
detection (Sivic and Zisserman, 2003; Lowe, 2004),
and near-duplicate image/video detection (Sivic and
Zisserman, 2003; Douze et al., 2010). Keypoints have
been defined as the local extremas of certain measure-
ment, which ensures their saliency and robustness to
various image transformations. In general, one key-
point feature only represents one local structure in an
image. It therefore has high chance of coinciding with
the canonical structure of an object, which makes it
possible to recognize objects by assembling their par-
tial views. Since the keypoint had been introduced,
this principle has been successfully adopted in differ-
ent object detection tasks on the textured images.
Many successes have been reported in different
contexts about keypoint features, unfortunately most
of the research about keypoint feature detection and
application has been concentrating on the texture im-
ages. Although the exploration on keypoint feature
can be partly attributed to the original search for cor-
ners in the less textured objects (Smith and Brady,
1995), few light has been truly shed on how to identify
and make use of keypoint features in the less textured
contexts. In contrast to the actual world with rich in
less textured visual objects, research has not concen-
trated on the detection of less textured object. Fig-
(a) Swan (b) Blox (c) X-ray imaging
on Lunggage
Figure 1: Typical examples of less textured objects with
Harris-Affine points displayed.
ure 1(a)-(c) show three typical examples of less tex-
tured objects. These types of objects are frequently
observed in different circumstances. The importance
of identifying these objects has been witnessed in re-
cent works (Hinterstoisser et al., 2012; Hinterstoisser
et al., 2009; Kim et al., 2007; Mery, 2011). However,
the existing detectors are unable to identify the local
structures correctly. For instance, as shown in Fig-
ure 1(a)-(c), although the Harris-Affine points in Fig-
ure 1(a)-(c) are roughly located in the object corners,
the characteristic scales estimated for the keypoints
are mostly wrong. This is mainly because there are
insufficient gradients around the corner. As a con-
sequence, meaningful local structures are no longer
desirable in these cases. Compared to object detec-
tion in the texture images, due to the lack of suitable
features, effective solution is still slow to occur in the
less textured cases.
Observing that it is hard to recover the correct
local structures on the less textured objects with ex-
isting detectors, we propose to identify them based
449
Zhao W., Byeon W. and M. Breuel T..
On the Detection and Matching of Structures on Less-textured Scenes.
DOI: 10.5220/0004275404490454
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 449-454
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

purely on an edge image. By returning back to orig-
inal way for corner detection, we basically identify
two types of local structures, namely corners (also
termed as junctions in some cases) and closed regions
(visually closed region or blob structures). We ob-
serve that these two types of structure already cover
most of identifiable local structures of an object. Our
approach achieves scale and affine invariances with-
out complicated scale and affine estimation (Mikola-
jczyk and Schmid, 2004) or simulation (Morel and
Yu, 2009). In addition, with the detected structure,
we are able to distinguish one compact local patch as
background and foreground side. Meanwhile, it also
allows to match either between compact local patches
or pure object contours.
The remainder of this paper is organized as fol-
lows. The related work about keypoint detection and
objects detection in less textured images has been re-
viewed in Section 2. Section 3 details the proposed
local structure extraction method in the less textured
scene. Section 4 presents the evaluation of proposed
keypoint features on standard benchmark in compar-
ison to representative keypoint detectors. Section 5
concludes our findings and overview our future work.
2 RELATED WORK
Corners have been recognized as the most salient and
robust structures latent in a visual object. Experi-
ments have shown that removing the corners from
images impedes human recognition, while removing
most of the straight edge information does not (Tuyte-
laars and Mikolajczyk, 2008). The general procedure
of corner detection involves the localization of corner
and the search for the underlying structure around the
corner. The latter makes it possible for feature rep-
resentation and afterwards matching among corners.
For edge based methods (Smith and Brady, 1995;
Mokhtarian et al., 1998; He and Yung, 2008), most
of the research (Smith and Brady, 1995; Mokhtarian
et al., 1998; He and Yung, 2008) are limited to lo-
calizing the corners, while further exploration on how
the complete corner structure can be utilized are left
untouched. In contrast, most of the saliency function
based approaches (Mikolajczyk and Schmid, 2004;
Tuytelaars and Mikolajczyk, 2008)are able to both lo-
calize and scale the corner structures. However, these
approaches are not suitable for less textured scenes.
As we know, in the saliency function based ap-
proaches, the detection of canonical structure of a
corner is achieved by automatic scale selection (Lin-
derberg, 1998), usually either trace or determinant
on Hessian matrix is adopted to select characteris-
(a) Corner and its characteristic
scales
(b) Saliency curves on Corner struc-
ture
Figure 2: Corner structure and its scale space saliency
curves defined on Hessian matrix (H). The charactertistic
scales are found at where Trace(H) and Det(H) attain their
local maxima respectively. The expected scale is illustrated
with dashed ellipse in (a).
tic scale in the scale space. In texture images, the
detected scales are not expected to perfectly cover
corners (Tuytelaars and Mikolajczyk, 2008). Once
the structure is functionally salient, the texture field
around the structure helps to distinguish it out. How-
ever, due to the lack of textures, this doesn’t hold
for less textured scenes. Figure 2(a) and (b) show
a corner structure and its saliency functions in scale
space respectively. As shown in Figure 2(b), due to
the lack of significant gradient levels, function peaks
correspond to visually insignificant scales. While the
expected scale (ellipse in dashed line in Figure 2(a))
has been missed. As a result, Trace(H) and Det(H)
either produce no meaningful scale (e.g., Figure 1(b)
and (c)) or detect multiple characteristic scales around
one corner (e.g., Figure 1(c)).
Besides the risk of missing object true structure
in the less textured image, the performance of corner
detector can also be affected by complex background
on which the object lies. In general, corners are of-
ten found near object boundaries as this is where the
intensity change usually occurs. The region extrac-
tion process is often based on measurements on non-
planar structures, e.g., including background or an-
other facet of the object (Tuytelaars and Mikolajczyk,
2008). In these cases, the robustness to background
changes will be affected for most of existing detec-
tors (Tuytelaars and Mikolajczyk, 2008).
In (Pantofaru et al., 2006), region based context
feature is proposed to cope with the less textured ob-
jects. It models the relationship between closed re-
gions and identify spatial proximityamong object fea-
tures. It aims to capture the object shapes and their
discriminative surface. However, it is still difficult to
obtain reliable feature regions and proper structure of
the object due to unstable segmentations.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
450

3 EDGE BASED DETECTION OF
LOCAL STRUCTURES ON LESS
TEXTURED OBJECT
3.1 Pre-processing
The procedure of keypoint extraction begins with
the edge detection. Canny edge detection algo-
rithm (John, 1986) is first applied on the input im-
age. The choice of Canny edge detection is mainly
due to its simplicity and stability in different situa-
tions. In order to ensure the detected edge is ex-
actly one pixel wide, the edge detection results are
further processed with thinning algorithm proposed
in (Zhang and Wang, 1996). Followed by the thin-
ning, the bitmap of edges has been parsed into graph
representation. In the graph representation, we main-
tain the original connectivity and sequential orders of
the pixels along the edges. After this pre-processing,
each disconnected contour is ready and will be treated
independently for local structure detection in the later
stages.
3.2 Corner Detection
There are several ways available for corner detection
along object contours (Mokhtarian et al., 1998; Nak-
agawa and Rosenfeld, 1979; Liu et al., 2009; He and
Yung, 2008). Most of the approaches define corners
on the local maximum of the edge curvature. After
a comparative study over the effectiveness of differ-
ent definitions about the curvature, we adopt approach
presented in (Nakagawa and Rosenfeld, 1979). Ac-
cording to (Nakagawa and Rosenfeld, 1979), the cur-
vature in edge pixel P(x,y) can be defined as
θ = |arctan(
y
2
− y
1
x
2
− x
1
)|, (1)
where P
b
(x
1
,y
1
) and P
f
(x
2
,y
2
) are points W
0
pixels
before and after the current pixel P respectively along
the edge. W
0
is empirically set to 7 and kept the same
across all our experiments in the paper. With the help
of Eqn. 1, curvature of each pixel along the edge can
be sequentially calculated and kept in order. Then this
curvature sequence has been undergone several runs
of linear smoothing. Followed by the smoothing, the
corner detection starts from either ends of the edge
segment. The edge points are recognized as corners
when they attain the local maximum on Eqn. 1. Since
each disconnected edge is treated separately, process
above has been repeated on each edge curve.
As observed in Figure 3(b), the detected corner
point (e.g., c
1
, c
2
or c
3
) carries very limited informa-
tion if we view them alone. As a matter of fact, it
is the curved structure centering on the corner (e.g.,
curve dc
1
c
2
and dc
2
c
3
in Figure 3(b)) distinguishes the
corner (e.g., c
2
in Figure 3) out. Based on this obser-
vation, we integrate two neighboring segments with
the corner as a uniform local structure. This time
the corners we discovered are the local curved struc-
tures. For each corner structure, the concave side can
be approximated by an inscribed triangle which con-
nects the three consecutive corners (e.g., c
1
, c
2
and c
3
in Figure 3(b)). Furthermore, the affine region over
this local structure can be approximated by a circum-
scribed ellipse of this triangle. The ellipse is known
as Steiner ellipse (Kimberling and Hofstadter, 1998)
which is defined in Eqn. 2.
a(x− x
0
)
2
+ b(x− x
0
)· (y− y
0
)+ c(y− y
0
)
2
= 1, (2)
where
x
0
=
x
1
+ x
2
+ x
3
3
, y
0
=
y
1
+ y
2
+ y
3
3
Additionally, we define matrix B as
B =
(x
1
− x
0
)
2
(x
1
− x
0
) · (y
1
− y
0
) (y
1
− y
0
)
2
(x
2
− x
0
)
2
(x
2
− x
0
) · (y
2
− y
0
) (y
2
− y
0
)
2
(x
3
− x
0
)
2
(x
3
− x
0
) · (y
3
− y
0
) (y
3
− y
0
)
2
,
(3)
and B
i
(i = 1, 2,3), which shares all the elements with
B except that the ith column has been replaced by
(1,1,1)
T
. The parameters in Eqn. 2: a, b and c can be
determined by Eqn. 4.
a =
Det(B
1
)
Det(B)
,b =
Det(B
2
)
Det(B)
,c =
Det(B
3
)
Det(B)
, (4)
where Det(·) is the determinant of a matrix. Up-to-
now, the corner structure has been approximated by
an affine region. The affine invariance now becomes
achievable if we assume this affine region has been
transformed from a structure norm by linear transfor-
mation based on Eqn. 5.
T =
a b/2 0
b/2 c 0
0 0 1
(5)
Figure 3 demonstrates the process of corner detection
and affine region approximation. Especially, the de-
tected local structure that has been normalized by the
T
−1
is shown in bottom right of Figure 3(b).
3.3 Closed Region Detection
Although in the edge image, salient structures of an
object can be largely decomposed into corners, there
is still another type of local structure we fail to cover.
For example, no corner will be detected on a circle
OntheDetectionandMatchingofStructuresonLess-texturedScenes
451

(a) X-ray imaging on a handgun (b) Detect corners on an edge from (a)
Figure 3: Corners detection on Canny edge of input image.
since the curvatures along the edge are constant. In
other cases, corners can be detected while we still
miss the local structure as a whole, since corners are
overheadly decomposed. Intuitively the more compli-
cated the local structure is, the more distinguishable
it is. As a result, detecting this type of local struc-
ture which has been missed in corner detection is also
expected.
Observing that these local structures appear as
closed curve with arbitrary shapes in the edge image.
Our algorithm only considers edge segment open on
one side. In the case that the expected closed segment
has been broken in several ways, we believe they can
still be roughly approximated by corners individually.
The problem of detecting closed (or semi-closed)
curve region can be generalized into a traditional
shortest path searching between any two end-points in
the connected edge segments. The end-point refers to
either end-point of a segment or a junction at which
more than one segment joins with each other. They
are treated as vertex in a graph representation. Sim-
ilarly, the segment which connects two end-points is
treated as an edge in between two vertices. The edge
weight is consequently assigned to the length of the
segment. Shortest path searching is therefore exhaus-
tively undertaken for all the end point pairs. Since
we have limited number of vertices in the graph, the
detection can be fulfilled efficiently.
As noticed before, the closed region R would be
in an arbitrary shape and orientation. As a result, di-
rect matching of one closed region with its linearly
transformed counterpart involves probing the whole
transformation space (anisotropic scaling and rota-
tion), which is in prohibitively high cost. To handle
this issue, similar to corner detection, we superimpose
an approximated affine region on the detected closed
(or nearly closed) structure. This is done by collect-
ing all the points which fall inside the region. Such
that the covariance matrix in Eqn. 6 defined on these
points regularizes an ellipse centering on the region
center µ(R).
Σ(R) =
1
|R|
∑
x∈R
(x− µ)(x− µ)
T
, (6)
(a) Canny edge from
Figure 1(b)
(b) Corners found on
(a)
(c) Closed Regions
found on (a)
Figure 4: Corners and closed regions detected from input
edge image.
where
µ(R) =
1
|R|
∑
x∈R
x. (7)
Similar to corner structure, with the help of the affine
adaptation, the detected closed region can be nor-
malized. Visually relevant regions which have been
affinely transformed become comparable once being
normalized with their Σ
−1
(R)s respectively.
3.4 Detect Local Structure in Multiple
Scales
Traditionally, the purpose of detecting keypoints in
multiple scales is to select a proper characteristic
scale on which the saliency function attains local ex-
trema. Similar local structures will coincide on simi-
lar characteristic scales, such that the local structures
with different scaling are comparable to each other.
Thus, scale invariance is achieved. In our case, both
the corner and closed region maintain the same shape
under arbitrary isotropic scaling. Once normalizing
the local structure into fixed-size patch (e.g., 41 × 41
in SIFT (Lowe, 2004)), scale invariance is achiev-
able. However, according to scale space theory (Lin-
derberg, 1998), the purpose of detecting keypoints in
multiple scales in its nature is to simulate the vision
effect of viewing objects from different distances. In
our case, object contour varies when it has been ob-
served from different distances. Edge detection un-
der different scales may generate different object con-
tours and this in turn results in different local struc-
tures. As a consequence, detecting corners and closed
region in multiple scales could help us to identify dif-
ferent local structures as much as possible. More im-
portantly, if a group of local structures are repeatedly
observed that are located in the same contour, the lay-
out of object parts can be captured. As a result, de-
tecting local structures in multiple scale also helps us
to relate local stuctures according to object layout. In
the implementation, the scale space is simulated by
varying σ
k
increasingly (σ
k
= k·σ
0
,k = 1,2, ...) while
the ‘low’ and ‘high’ thresholds are fixed to 0.15 and
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
452
(a) Corners (b) Closed Regions
Figure 5: Local structures detected (6 scales and 3 octaves)
on the first image of Graffiti sequence.
0.75 respectively. To ensure the stableness of detected
structures, only structures appear in at least two con-
secutive scales are kept. In addition, similar to (Lowe,
2004), it is no need to keep the image in its original
size when σ
k
is considerably high. The scale space is
actually simulated by three octaves. In each octave,
four scales with increasing σ
k
are generated.
4 OBJECTS RECOGNITION IN
LESS-TEXTURED AND
TEXTURE RICH SCENES
The experiments in this section investigate the effec-
tiveness of the proposed local feature against differ-
ent transformations under object recognition task. In
order to have a clear picture about its suitability in
different contexts, the experiments are conducted on
both textured and structured (less textured) images.
Similar to (Mikolajczyk et al., 2005), we investigate
the repeatability score of the proposed detector (de-
noted as ‘corner’) in comparison to popular detec-
tors which achieve scale and affine invariance. They
are namely Harris-Affine (Mikolajczyk and Schmid,
2004) based on saliency function, IBR (Tuytelaars
and Gool, 1999) and EBR (Turina et al., 2001) which
are based on image edges, and Salient region (Kadir
et al., 2004) that is based on image intensity lev-
els. The following experiment is conducted based
on the image sequences and testing software provided
by K. Mikolajczyk (Mikolajczyk and Schmid, 2005).
The transformations incorporated in these image se-
quences range from viewpoint changes, scaling and
rotation to different levels of blur. In each transforma-
tion type, detectors are tested with both structured and
textured scenes. Detected corners and closed regions
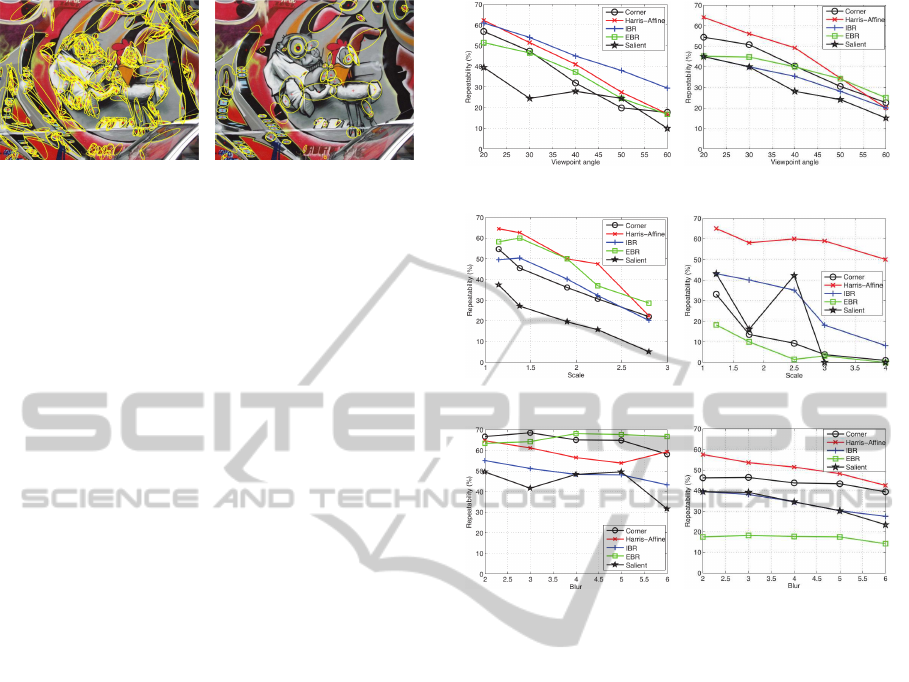
on ‘Graffitti’ image are shown in Figure 5. For the
structures extracted by other detectors (Harris-Affine,
IBR, EBR and Salient region), please refer to (Miko-
lajczyk et al., 2005).
As shown in Figure 6, Harris-Affine overall out-
performs other detectors, while Salient region are in-
(a) Viewpoint change for structured:
Graffitti sequences
(b) Viewpoint change for textured
scene: Wall sequences
(c) Scale for the structured scene:
Boat sequences
(d) Scale for the textured scene:
Bark sequences
(e) Blur for the structured scene:
Bikes sequences
(f) Blur for the textured scene: Trees
sequences
Figure 6: Repeatability of Local structures in comparison to
popular keypoint detectors under different transformations.
effective in most of the cases. Compared to the per-
formances in structured scenes, all edge based ap-
proaches (corner, IBR and EBR) suffer considerable
performance drops under the scenes that are full of
textures. The instability of these approaches is mainly
due to the low reliability of edge detection in tex-
tured scene. However, if we consider these struc-
tured scenes only, the proposed approach demon-
strates more stable performances than others in less
textured scenes. This implies our approach is rather
suitable on structured (shown in figures on the left
column) than the textured cases. Although Harris-
Affine demonstrates stable performance in terms of
repeatability, due to the reason explained in Section 2,
it is not really promising for less textured scene,
which will be verified in our second experiment.
5 CONCLUSIONS
We have presented our approach on extracting salient
local structures, namely corners and closed regions,
in less textured scenes. As illustrated in the paper,
OntheDetectionandMatchingofStructuresonLess-texturedScenes
453

these features can be easily adapted with the local ob-
ject structures and demonstrate stable performances
in less textured scenes. Moreover, as they are derived
from object contours, these structures have the flex-
ibility of allowing different levels of abstraction on
the descriptors. To alleviate the instability of image
contour detection and apply this feature extraction on
different object types are the directions to explore in
the future.
ACKNOWLEDGEMENTS
This work is part of the SICURA project supported
by Federal Ministry for Education and Research, Ger-
many with ID FKZ 13N11125.
REFERENCES
Douze, M., J´egou, H., and Schmid, C. (2010). An image-
based approach to video copy detection with spatio-
temporal post-filtering. IEEE Transactions on Multi-
media, 12(4):257–266.
He, X. C. and Yung, N. H. C. (2008). Corner detector based
on global and local curvature properties. Optical En-
gineering, 47(5).
Hinterstoisser, S., Cagniart, C., Ilic, S., Sturm, P., Navab,
N., Fua, P., and Lepetit, V. (2012). Gradient response
maps for real-time detection of texture-less objects.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 34(5):876–888.
Hinterstoisser, S., Kutter, O., Navab, N., Fua, P., and Lep-
etit, V. (2009). Real-time learning of accurate patch
rectification. pages 2945–2952.
John, C. (1986). A computational approach to edge detec-
tion. IEEE Transactions on Pattern Analysis Machine
Intelligence, 8(6):679–698.
Kadir, T., Zisserman, A., and Brady, M. (2004). An affine
invariant salient region detector. In In Proceedings
of the 8th European Conference on Computer Vision,
pages 345–457.
Kim, G., Hebert, M., and Park, S.-K. (2007). Preliminary
development of a line feature-based object recognition
system for textureless indoor objects. Recent Progress
in Robotics: Viable Robotic Service to Human.
Kimberling, C. and Hofstadter, D. (1998). Triangle cen-
ters and central triangles. Number 129 in Congressus
numerantium. University of Manitoba.
Linderberg (1998). Feature detection with automatic scale
selection. International Journal of Computer Vision,
30(2):79–116.
Liu, J., Jakas, A., AI-Obaidi, A., and Liu, Y. (2009). A
comparative study of different corner detection meth-
ods. In IEEE International conference on Computa-
tional intelligence in robotics and automation, pages
509–514.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. International Journal on Com-
puter Vision, 60(2):91–110.
Matas, J., Chum, O., Urban, M., and et. al (2002). Robust
wide baseline stereo from maximally stable extremal
regions. In British Machine Vision Conference, pages
384–393.
Mery, D. (2011). Automated detection in complex objects
using a tracking algorithm in multiple x-ray views. In
IEEE Workshop on Object Tracking and Classifica-
tion Beyond the Visible Spectrum in Conjunction with
Computer Vision and Pattern Recognition, pages 41–
48.
Mikolajczyk, K. and Schmid, C. (2004). Scale and affine in-
variant interest point detectors. International Journal
of Computer Vision, 60:63–86.
Mikolajczyk, K. and Schmid, C. (2005). A perfor-
mance evaluation of local descriptors. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
27(10):1615–1630.
Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,
Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L. V.
(2005). A comparison of affine region detectors. Inter-
national Journal of Computer Vision, 65(1-2):43–72.
Mokhtarian, Farzin, and Suomela, R. (1998). Robust im-
age corner detection through curvature scale space.
IEEE Transactions on Pattern Analysis Machine In-
telligence, 20(12):1376–1381.
Morel, J.-M. and Yu, G. (2009). ASIFT: A new framework
for fully affine invariant image comparison. SIAM
Journal on Imaging Sciences, 2(2):438–469.
Nakagawa, Y. and Rosenfeld, A. (1979). A note on polyg-
onal and elliptical approximation of mechanical parts.
Pattern Recognition, 11:133–142.
Pantofaru, C., Dorko, G., Schmid, C., and Hebert, M.
(2006). Combining regions and patches for object
class localization. pages 23–30.
Sivic, J. and Zisserman, A. (2003). Video google: A text
retrieval approach to object matching in videos. In
IEEE International Conference on Computer Vision,
pages 1470–1477.
Smith, S. M. and Brady, J. M. (1995). Susan - a new ap-
proach to low level image processing. International
Journal of Computer Vision, 23:45–78.
Turina, A., Tuytelaars, T., and Gool, L. V. (2001). Effi-
cient grouping under perspective skew. In IEEE Inter-
national Conference on Computer Vision and Pattern
Recognition.
Tuytelaars, T. and Gool, L. V. (1999). Content-based im-
age retrieval based on local affinely invariant regions.
In In International Conference on Visual Information
Systems, pages 493–500.
Tuytelaars, T. and Mikolajczyk, K. (2008). Local Invariant
Feature Detectors: A Survey. Now Publishers Inc.,
Hanover, MA, USA.
Zhang, Y. Y. and Wang, P. S. P. (1996). A parallel thin-
ning algorithm with two-subiteration that generates
one-pixel-wide skeletons. In IEEE International Con-
ference on Pattern Recognition, pages 457–461.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
454
