A New Approach to Prevent Deadlock in S
3
PR Nets with Unreplicable
Resources
Asaftei Timotei
1
and Jos
´
e-Manuel Colom
2
1
Department of Automatic Control and Industrial Informatics, Technical University ”Gh. Asachi”, Iasi, Romania
2
Arag
´
on Insitute of Research, Engineering (I3A), University of Zaragoza, Zaragoza, Spain
Keywords:
S
3
PR, Deadlock Prevention, Minimal Siphons, Pruning Graph.
Abstract:
Deadlock prevention in Resource Allocation Systems with shared resources represents an important goal in
systems design. When using Petri net based modeling, typical methods for attaining this goal use syphon
analysis. This paper develops a new method to prevent deadlock in S
3
PR nets based on minimal siphons
and Pruning Graphs. The method consists in two steps: first is the increasing of the number of copies of
a replicable resource and second is the splitting of the total copies of the replicable resources. We use the
Pruning Graph to choose the replicable resources we are going to split. The algorithm uses only structural
information of the net and a simple example is used to illustrate its application.
1 INTRODUCTION
In general, health care enterprise processes have been
managed using limited forms of work flow. Some
example of these work flow are the clinical and ad-
ministrative protocols. These protocols use a limited
number of resources. Health care enterprise processes
can be seen as a particular type of systems: Resource
Allocation Systems. A very common problem which
occurs in these systems is the problem related to the
reachability of deadlock states. Deadlock states are
unacceptable scenarios in the normal work of this
kind of systems, because its existence means that a
set of activated processes cannot be finished because
each one needs a resource that is allocated to other
process in the same set.For these systems, the use of
Petri Net models has been proven very convenient for
the formal modeling and further analysis and correc-
tion of the their models.
In the last years many works (Chao, 2010),
(Ezpeleta et al., 1995) have been devoted to develop
formal methodologies able to detect these bad behav-
iors and introduce modifications in the original design
in such a way that is possible to guarantee that a dead-
lock state never will be reached. In particular, two im-
portant subclasses of Petri Nets have been defined for
modeling a wide class of Resource Allocation Sys-
tems: the S3PR nets (Ezpeleta et al., 1995) and the
S4PR nets (Tricas, 2003). For these classes of nets
characterizations of nonliveness have been obtained
that are based in the existence of certain structural ob-
jects named bad siphons that are the structural cause
of the appearing of the deadlock states. A bad siphon
is a set of places such that the set of input transitions
to these places is a subset of the output transitions of
these places. Therefore, if this set of places becomes
empty of tokens, it remains empty forever and all out-
put transitions are dead.
In this article we develop a new method to enforce
the liveness of the modeled system that it is not based
in the control of the bad siphons. The basic idea is
to transform the structure of the Petri Net in such a
way that the bad siphons disappear in the transformed
model. Therefore, if there are not bad siphons and the
net has an admissible initial marking then is live. To
conduct the computation of the structural transforma-
tions we will use the so called Pruning Relation be-
tween minimal siphons containing a unique resource
place. This relation is defined in (Cano et al., 2010)
for S4PR nets. Therefore, the resources to be split
must guarantee that the resulting Pruning Graph does
not contain a strongly connected subgraph character-
izing a minimal siphon.
We will see that this new technique is a different
strategy to those inspired in Control Theory because
we do not forbid states by constraining the allocation
of resources. This technique increases the set of states
giving rise to the appearing of new exit states from
104
Timotei A. and Colom J..
A New Approach to Prevent Deadlock in S3PR Nets with Unreplicable Resources.
DOI: 10.5220/0004275702520257
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 252-257
ISBN: 978-989-8565-40-2
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

each old deadlock state. This property makes that this
technique cannot be applied in a non-discriminated
way in the domain of Flexible Manufacturing Sys-
tems because the own nature of the resources. Never-
theless, in the context of the logistic inside a hospital
it seems a viable strategy to prevent the appearing of
deadlocks.
The article is organized as follows. Section 2 in-
troduce some preliminary concepts and an example
of an S
3
PR. Section 3 presents some introductive no-
tions and the motivation for this paper. In section 4
the main results of this paper are presented: the split-
ting of the siphons algorithm and the liveness enforc-
ing algorithm. Finally some conclusions are given in
section 5.
2 PRELIMINARIES
2.1 Petri Nets - S
3
PR
A nonempty set D ⊆ P is a siphon if
•
D ⊆ D
•
. A
siphon is a non-empty set of places which are con-
nected via transitions. One property of the siphons is
that once there is no token inside the places, it is not
possible to gain tokens coming from the rest of the
net.
We say that a siphon S is minimal if it does not
contain another siphon as a proper subset. In a min-
imal siphon it must exists at least two places; other-
wise the structure remained can not be considered a
siphon.
Definition 1. A system of Simple Sequential Pro-
cess with Resources (S
3
PR) N = O
k
i=1
N
i
= (P ∪ P
0
∪
P
R
, T, F) is defined as a union of a set of nets N
i
=
(P
i
∪{p
0
i
}∪ P
R
i
, T
i
, F
i
) sharing common places, where
the following conditions are true:
1. p
0
i
is called the process idle places on N
i
. P
i
and P
R
i
are called operation places and resource
places;
2. P
i
6=
/
0; P
R
i
6=
/
0; p
0
i
∈ P
i
; (P
i
∪ {p
0
i
}) ∩ P
R
i
=
/
0;
3. ∀p ∈ P
i
, ∀t ∈
•
p, ∀t
0
∈ p
•
, ∃r
p
∈ P
R
i
,
•
t ∩ P
R
i
=
t
0•
∩ P
R
i
= {r
p
};
4. ∀r ∈ P
R
i
,
••
r ∩ P
i
= r
••
∩ P
i
6=
/
0,
•
r ∩ r
•
=
/
0;
5.
••
(p
0
i
) ∩ P
R
i
= (p
0
i
)
••
∩ P
R
i
=
/
0;
6. N
0
i
is a strongly connected state machine, where
N
0
i
= (P
i
∪{p
0
i
}, T
i
, F
i
) is the resulting net after the
places in P
R
i
and related arcs are removed from
N
i
;
7. Every circuit of N
0
i
contains the place p
0
i
8. Any two N
i
are composable when they share a set
of common places. Every shared place must be a
resource place.
For example in Figure 2 there is an example of an
S
3
PR network.
Definition 2. Let N = hP ∪ p
0
∪ P
R
, T, Fi be a S
3
PR.
A initial marking m
0
is called an acceptable initial
marking for N if:
1. m
0
(p
0
) ≥ 1;
2. m
0
(p) = 0, ∀p ∈ P;
3. m
0
(r) ≥ 1, ∀r ∈ P
R
The definition points out that the acceptable mark-
ing is the marking for which the net has at least one
token in the idle place and at least one token in ev-
ery resource place (there is at least one copy of ev-
ery resource in that system). In S
3
PR there is no
a direct characterization of the liveness property but
some known results present characterizations of the
non-liveness of a net. In (Tricas, 2003) there are pre-
sented two theorems characterizing non-liveness of
S
4
PR nets.
2.2 An Introductory Example
In this article the example of an hospital will be con-
sidered, as in Figure 1. The elements from the hos-
pital considered will be the reception (PW) where the
patients are received and the administrative paper is
done, the consulting room (CR) where a doctor gives
the diagnostic to the patients, the surgery room (S)
where the surgeries of the patients are done and the
doctor (D) who will do all these procedures. It will be
considered that the person who work at the reception
and the doctor could serve one person at the time; in
the consulting room and in the surgery room only one
patient could be treated at the time too, i.e. we can
say that the capacity of them is equal to one.
If we want that the hospital to work in good con-
ditions, some protocols have to be respected by the
patients and the hospital stuff. The hospital has two
entrance: a normal one and the emergency one. The
patients who come at the normal entrance (IN1) have
to go first to the reception (PW - paper work). De-
pending on the problems(illness, disease) the patients
have, they can be sent to the consulting room (CR) or
to the surgery room (S). After the patients finish with
either one of these, they go to see doctor (Dr) for the
releasing certificate. With all these things done, the
patients can leave the hospital (OUT1). The hospital
has another entrance (IN2): for the emergency cases.
The patients who came at IN2, they are checked by
the doctor (D), and after that send to the surgery room.
From the surgery room they have to fill the papers, so
ANewApproachtoPreventDeadlockinS3PRNetswithUnreplicableResources
105

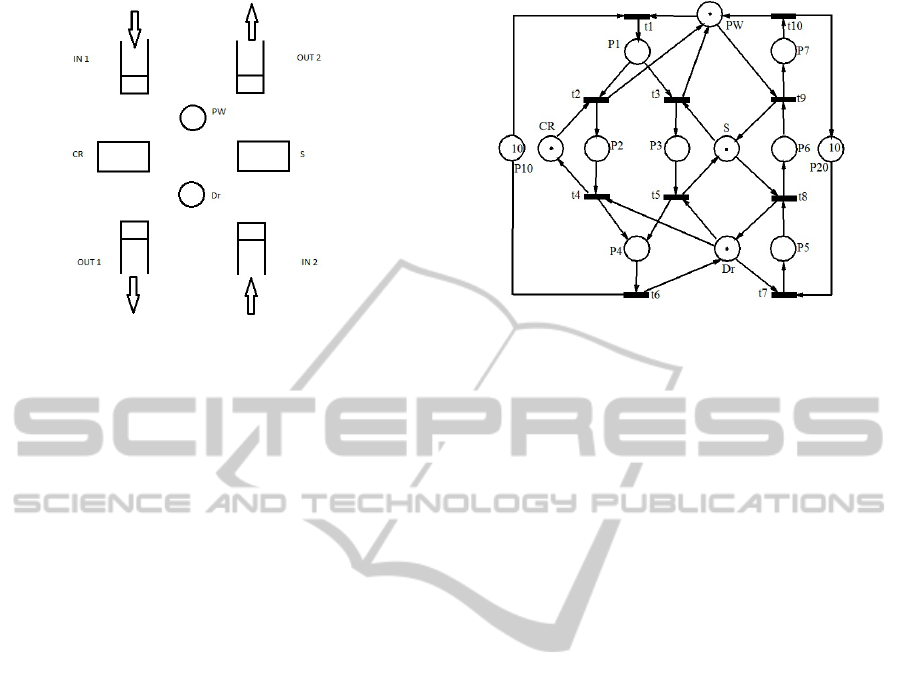
Figure 1: The layout of the hospital.
they have to go to PW first, and after that they can go
home. Basically, in this hospital, only this two sce-
narios can be encountered.
Figure 2 presents the Petri net model of the work-
ing plan of the hospital. The two cases presented
in this hospital, share the four resources: consult-
ing room, surgery room, the person who do the pa-
per work and the doctor. Each of the resources are
represented by means of places. Places P
10
and P
20
are initialized with a value equal to ten. That means
the number of patients who can be treated simul-
taneously. The model of the hospital is a particu-
lar one. It belongs to the class of S
3
PR nets. We
are interested in the liveness of this net. The live-
ness of this class net is related to the existence of
empty siphons (insufficiently marked) at the marking
m. For example, in this net there are siphons which
are not sufficiently marked. Let us consider the siphon
S
1
= {PW, Dr, CR, S, P
4
, P
7
} that under the marking
m = P
1
+ P
2
+ P
3
+ P
5
, +8 · P
10
+ 9 · P
20
becomes un-
marked.
In this paragraph the terms of replicable and non
replicable resources will be defined. We said that a
resource is replicable (P
R
R
) if in the Petri net we can
add another place(by adding a new place in the Petri
net we add a new object; identical as structure and
as functions). A resource is un-replicable (P
R
U
) if no
place can be added in the Petri net; the object repre-
sented by this non replicable place is unique.
In (Cano et al., 2010) all the resource places was
considered replicable but for this article we consider
that a part of the resources are replicable and a part
are un-replicable. If we consider the example form
Figure 1 and take in consideration the surgery room
(S) as an un-replicable resource, then if the room is
occupied by a patient, the new patient who arrives,
has to wait for the room to be released. The reason
why these resources from our system are, in general,
Figure 2: The Petri Net modeling the function of the hospi-
tal.
un-replicable is because they are unique or too im-
portant i.e. the surgery room (S) - there are a lot of
expensive equipments and the hospital can not afford
another room like this; the doctor (D) - is a very good
doctor and there is no doctor in the hospital who can
perform a surgery like he does.
3 THE NEW APPROACH
The approach presented in this paper share some ad-
vantages of the previously liveness enforcing tech-
niques that are based in the increasing of the number
of available resources at the initial marking or tech-
niques in which monitor places are added. Next, there
are briefly presented two of these methods.
A. Increasing the Number of the Resources
Increasing the number of the tokens for each resource
in the initial marking. This method it is not very good
because once we increased the number of resources,
we can increase the number of the ”customers”. By
increasing both the number of resources and the num-
ber of ”customers” the deadlock can appear again. In
other words, liveness is not monotonic with respect
of customers (the initial marking of the idle places).
Nevertheless, liveness in S
3
PR is monotonic with re-
spect to the number of resources.
B. Forbidden States Removing Method
This method has been classified traditionally inside
the deadlock prevention techniques (Hou et al., 2010)
and has been implemented using different strategies.
For example, using monitors places that can be inter-
preted as virtual resources; supervisory control (Lee
et al., 2005),(Wang et al., 2010),(Reveliotis, 2007)
strategies as marking dependent assertions guarding
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
106

Figure 3: The Pruning Graph for the S
3
PR from Figure 2
when there are unreplicable resources.
the firing of transitions. In all cases, this method
looks to remove all states that can be considered as
bad states. A bad state is a state where a token in
a process place is deadlocked forever or a marking
that inevitably leads to one of the previous one. In
the general case, this goal can not be reached because
for some remaining states is possible that some legal
states must be removed too. In the literature, there ex-
ist many papers presenting different tactics that try to
minimize the numbers of legal states that must be re-
moved in order to enforce the liveness property using
different permissiveness criteria (Li and M., 2008).
C. The New Approach
The approach proposed in this paper save the two pre-
vious drawbacks obtaining the advantages of the two
approaches. That is, we increase the number of re-
sources (the resources which are replicable) in order
to enforce the liveness without the reduction of the
concurrency of the system. Next the general steps of
the algorithm will pe presented:
1. Identification of a replicable resource belonging
to a bad siphon that can give rise to the appearing
of a deadlock state.
2. Classification of the holder places of the selected
replicable resources in two disjoint groups. That
is, the method proceeds increasing the number of
replicable resources but these new resources will
be used in a private way by only one of the clas-
sified groups. This is the idea of specialization of
the new resources.
3. Definition of two new resource places and remov-
ing the old one. Each one of these new resource
places has one the previous sets of holder places
and they are connected to the input and output
transitions of the holder places in the same way
than the original resource place. Observe that now
there exist two different types of resources where
previously existed only one type of resources. The
copies of each type of resource are used in a
private way by the corresponding set of holder
places.
4. Introduction of the same number of tokens in each
new resource place than the number of copies of
resources in the original resource place.
The method can be considered a structural one be-
cause the splitting of the original replicable resource
places into two new places is done in such a way that
the siphon is broken or at least, in what concerns to
the considered resource place, the siphon has been re-
duced. Therefore, proceeding with all bad siphons in
the same way we can obtain a net without bad siphons
and then by the non-liveness theorem of S
3
PR nets,
the admissibly marked net must be live: the method
enforces liveness.
Observe, that the method increases the number
of resources (replicable resources) although they are
used in a private way with respect to the way they are
used in the original net. This means that the method
does no cut bad markings, the method introduces new
states allowing to go out from the old deadlock states.
That is, the old deadlock states are reached but now
there are enough resources (that they are used in a
private way) to go out to a new state saving the bad
scenario. In classical control theory, probably, this
strategy is unsatisfactory because the strategy there is
to forbid all bad states and all states that inevitably
lead to a bad state. Nevertheless, in other application
domains as in the hospital logistics the important goal
is to reach a complete treatment for the patient, adding
all needed resources to reach this goal.
The method presented in the next sections try to
solve some technical questions in order to reduce the
number of resources to be added in order to enforce
the liveness of the net.
4 THE LIVENESS ENFORCING
ALGORITHM
4.1 Properties and Lemmas
In this section some properties and lemmas will be
presented.
Lemma 1. Let N be a S
3
PR net, D ⊆ P a minimal
siphon of N and D
R
= D ∩ P
R
are the resource places
of D. D is the unique minimal siphon of N containing
exactly the set of resource places D
R
= D ∩ P
R
.
Proof. In (Cano et al., 2010) the statement for the
lemma was proven for the more general class of S
4
PR.
Taking into account the S
3
PR is a strict subclass of
S
4
PR, the results holds also for S
3
PR.
Lemma 2. Let N be a S
3
PR net. For each r ∈ P
R
there
exists a minimal siphon D
r
, such that D
r
=k y
r
k
ANewApproachtoPreventDeadlockinS3PRNetswithUnreplicableResources
107

For the algorithm that will be presented in this ar-
ticle, the concept of pruning relation between siphons
will be used. The siphons we are working in this arti-
cle are the minimal siphons as depicted in lemma 3. It
is obviously that the union of two minimal siphons is
a siphon, but in general it is not a minimal. Let us con-
sider two siphon: S
a
and S
b
. We say that the siphon
S
a
prunes S
b
if and only if the two siphons share some
transitions (T
ab
= S
a
∩ S
b
6=
/
0) and there exists com-
mon transitions with an input process place belonging
to S
b
and also the resource a inputs to these transitions
(U
a
= a
•
∩ T
ab
∩ (
•
T
ab
∩ S
b
∩ P
s
)
•
6=
/
0).
The elements which can be pruned from the
siphon S
b
by the siphon S
a
are under the form (t,
•
t ∩
P
s
) where t ∈ U
a
. The positions that can be removed
are ones of the form
•
t ∩ P
s
. These places can be
removed because they are non-essential siphons in
S
a
∪ S
b
.
Definition 3. Let N be a S
3
PR net and P
R
the resource
places of the net. The Pruning Graph (PG) of N is a
graph G = (V, E) where:
1. V = P
R
2. E ⊆ V ×V and ∀a, b ∈ P
R
, a 6= b, (a, b) ∈ E if U
a
=
a
•
∩ T
ab
∩ (
•
T
ab
∩ S
b
∩ P
s
)
•
6=
/
0 with T
ab
= S
a
∩
S
b
6=
/
0
3. The resources replicable will be represented as
circles and the un-replicable resources will be
represented by squares.
Once we considered that there is a difference be-
tween the resource places from the Petri net (replica-
ble and un-replicable resources), then between these
two Pruning Graphs will appear some differences. We
will denote the non replicable resource places with a
square and the replicable resources with a circle.
If we consider the example where some of the re-
source are un-replicable then the Pruning Graph will
look like in Figure 3 and as representation, the un-
replicable resource is marked with an square instead
of a circle. It can be noticed that the relations between
the nodes are still the same; the pruning relations be-
tween the resource places does not modify.
4.2 The Algorithms
The pruning relation between siphons, the Pruning
Graph and the labeling function for a S
3
PR net were
defined in the previous section. For this new approach
of liveness enforcing we need an algorithm which de-
scribes how the splitting is done in the S
3
PR. The
splitting is needed in the S
3
PR so there will appear
new replicable resources. With these replicable re-
sources the deadlock state is avoided. The idea is that
after the construction of the initial Pruning Graph of
the S
3
PR, we need to find and eliminate all circuits
from the net. An elimination in the Pruning Graph
will be equivalent with a new replicable resource in
the S
3
PR (replicable resource added by splitting an
existing replicable resources). For this article we will
consider the case where two un-replicable resources
can not be situated one next to another, but between
them there must be at least one replicable resource.
Definition 4. Let N be a S
3
PR net and G = (V, E) the
pruning graph of N. We call the multiplicity of an arc
e ∈ E the cardinal of the label of e.
Next, an algorithm of splitting the siphon will be
presented. For this algorithm we consider r ∈ P
R
\P
R
U
is the resource we are working on.
Algorithm 1. The splitting of a replicable resource.
Input: replicable resource r which belongs at least to
one circuit, N, the Pruning Graph of N;
Output: N
0
, r is substituted with r
1
and r
2
;
1. Delete r and all arcs between r and the transitions
t
i
, t
i
∈ {r
•
∪
•
r};
2. Add places r
1
and r
2
in S
3
PR;
3. Connect place r
1
with the net such that all the in-
puts of v
i
are the inputs of v
1
i
: ∀(s, r) ∈ E and
∀p ∈ P
S
such that (t, p) ∈ L((s, r)) add an arc from
r
1
to all t ∈
•
p and an arc from each t ∈ p
•
to r
1
;
4. Connect place r
2
with the net such that all the out-
puts of v
i
are the outputs of v
2
i
: ∀(r, s) ∈ E and
∀p ∈ P
S
such that (t, p) ∈ L((r, s)) add an arc from
r
2
to all t ∈
•
p and an arc from each t ∈ p
•
to r
2
;
For the Algorithm 2 we use the fact that the mul-
tiplicity of the arcs from the Pruning Graph will be
the same. Using this algorithm, all strongly connected
components(cycles) will be eliminated. One way for a
graph to became acyclic is to use reversed edges. The
problem of finding a set of smallest number of feed-
back edges is a problem called minimum feedback arc
set problem(Garey and Johnson, 1993). This is used
in our algorithm when we compute the minimal set of
arcs.
Algorithm 2. The liveness enforcing approach.
Input: Pruning Graph - PG, N, the nodes V, the edges
E;
Output: the new Pruning Graph - PG
0
, N
0
, V
0
;
1. Compute the pruning graph (PG) G(V, E) of the
N;
2. While G contains some cycles do
3. Compute a set of arcs W S = e
j
using a mini-
mum feedback arc set algorithm;
4. While W S 6= 0 do
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
108

Figure 4: The evolution of the Pruning Graph according to Algorithm 1 and Algorithm 2.
5. Take o node v
i
- replicable resource, from V
which is connected to e
j
in PG;
6. Modify N according to the Algorithm1;
7. Remove all arcs between v
i
and the nodes
next to it in PG;
8. Remove v
i
and put v
1
i
and v
2
i
;
9. W S = W S \ {e
j
}
10. Endwhile
11. Endwhile
From the the two algorithms above, it can be seen
that if the Pruning Graph is acyclic then the S
3
PR net
is live. But, in the most cases, the Pruning Graph has
cycles which have to disappear. The Pruning Graph
of the S
3
PR net from Figure 2 is depicted in Figure 3.
The S
3
PR net has three siphons: S
1
= {P
1
, PW, P
7
},
S
2
= {P
3
, S, P
6
} and S
3
= {P
4
, Dr, P
5
}. The goal of
the approach is to split the siphons. Because of the
restriction we put at the beginning, the siphon S
2
can
not be split because it contains an un-replicable re-
source. For the rest of the siphons where all the re-
sources are replicable the order we split the siphons
is random (until now it does not exist an algorithm to
describe the order the siphons have to be split). In this
example we consider that first we split siphon S
1
and
after that we split siphon S
3
. After these two splits,
the pruning graph become acyclic, so the algorithm
stops.
5 CONCLUSIONS
In this paper, based on the fact that deadlocks in S
3
PR
nets are related to unmarked siphons, we propose a
new approach to prevent the deadlock appearance.
The main contribution of this paper lies in the fact
that uses the advantages of the previous work on dead-
lock prevention, and introduce the concept of replica-
ble/unreplicalbe resources. The idea is to modify (by
splitting resource places) the petri net so in the corre-
sponded pruning graph will not left any strongly con-
nected components. One advantage for this method is
that we work with high level objects (siphons). Fur-
ther research may extend this algorithm to more gen-
eral nets as S
4
PR.
REFERENCES
Cano, E. E., Rovetto, C. A., and Colom, J. M. (2010). On
the computation of the minimal siphons of s
4
pr nets
from a generating family of siphons. In ETFA, pages
1–8.
Chao, D. Y. (2010). A simple modification of deadlock pre-
vention policy of s3pr based on elementary siphons.
In Transactions of the Institute of Measurement and
Control, volume 33, pages 93–115.
Ezpeleta, J., Colom, J.-M., and Martinez, J. (1995). A petri
net based deadlock prevention policy for flexible man-
ufacturing systems. IEEE Transactions on Robotics
and Automation, 11:173–184.
Garey, M. and Johnson, D. (1993). Crossing number is np-
complete. SIAM Journal of Algebraic and Discrete
Methods, 4:312–316.
Hou, Y., Liu, D., Li, Z., and Zhao, M. (2010). Deadlock pre-
vention using divide-and-conquer strategy for ws3pr.
In International Conference on Mechatronics and Au-
tomation (ICMA), pages 1635–1640.
Lee, J.-S., Zhou, M.-C., and Hsu, P.-L. (2005). An appli-
cation of petri nets to supervisory control for human-
computer interactive systems. In IEEE Transactions
on Industrial Electronics, volume 52, pages 1220–
1225.
Li, Z. and M., S. (2008). On the existence of a maxi-
mally permissive liveness-enforcing petri net supervi-
sor for flexible manufacturing systems. In IEEE In-
ternational Conference on Networking, Sensing and
Control (ICNSC), pages 90–95.
Reveliotis, S. A. (2007). Implicit siphon control and its role
in the liveness-enforcing supervision of sequential re-
source allocation systems. IEEE Transactions on Sys-
tems, Man, and Cybernetics, Part A, 37(3):319–328.
Tricas, F. (2003). Deadlock analysis, prevention and avoid-
ance in sequential resource allocation systems. PhD
thesis, University of Zaragoza, Zaragoza.
Wang, S., Wang, C., and Yu, Y. (2010). An algorithm to find
the condition on initial markings of resource places
and job places for liveness of s3pmr. In 8th IEEE
International Conference on Control and Automation,
pages 1445–1449.
ANewApproachtoPreventDeadlockinS3PRNetswithUnreplicableResources
109