Pose Estimation using a Hierarchical 3D Representation of Contours and

Surfaces

Anders Glent Buch

, Dirk Kraft

, Joni-Kristian K

ainen

and Norbert Kr

uger

Maersk Mc-Kinney Moller Institute, University of Southern Denmark, Odense, Denmark

Tampere University of Technology, Tampere, Finland

Keywords:

Pose Estimation, Shape Context Descriptors, Early Cognitive Vision.

Abstract:

We present a system for detecting the pose of rigid objects using texture and contour information. From

a stereo image view of a scene, a sparse hierarchical scene representation is reconstructed using an early

cognitive vision system. We deﬁne an object model in terms of a simple context descriptor of the contour

and texture features to provide a sparse, yet descriptive object representation. Using our descriptors, we do

a search in the correspondence space to perform outlier removal and compute the object pose. We perform

an extensive evaluation of our approach with stereo images of a variety of real-world objects rendered in a

controlled virtual environment. Our experiments show the complementary role of 3D texture and contour

information allowing for pose estimation with high robustness and accuracy.

1 INTRODUCTION

The pose estimation problem is a crucial aspect in

many vision, robotic and cognition tasks. Many sys-

tems solve the problem of obtaining the location of

the object of interest by tailoring the implementa-

tion to a speciﬁc object class or by relying on a spe-

ciﬁc feature type. Many 2D or image-based meth-

ods (Bay et al., 2006; Belongie et al., 2002; Lowe,

1999; Payet and Todorovic, 2011) learn an object

model by discretizing over the set of possible views

on an object, and base the detection on this represen-

tation. In 3D methods (Bariya and Nishino, 2010;

Drost et al., 2010; Hetzel et al., 2001; Johnson and

Hebert, 1999; Novatnack and Nishino, 2008; Papa-

zov and Burschka, 2010; Rusu et al., 2009; Stein and

Medioni, 1992; Wahl et al., 2003), there is a tendency

towards the use of range data which provides a large

set of surface points in the scene. Correspondences

between these points and a 3D model are then sought,

from which a pose is calculated.

We address the problem of estimating the pose of

rigid objects with known geometry and appearance

based on calibrated stereo image views of the ob-

ject. From the input stereo image, we reconstruct a

3D scene representation using an early cognitive vi-

sion system (Jensen et al., 2010; Pugeault et al., 2010)

covering contour and surface information.

Based on our features, we deﬁne relations be-

tween feature pairs. These relations encapsulate both

appearance and shape information. Inspired by (Be-

longie et al., 2002), we call the total set of relations

for a feature in a given spatial region a context. The

feature context descriptor is used for discriminative

correspondence search during pose estimation.

In Figure 1, we show the effect of combining both

contour points (blue) and surface points (red) in the

estimation process from a training view (top). Even

though contour information is adequate for obtaining

an alignment, it is clear that the quality of the ﬁt is

poor, which can be easily seen by the misaligned edge

contours which should be on the corner of the object.

In summary, the work described in this article

makes two main contributions:

1. The potential of using viewpoint invariant 3D re-

lations for pose estimation and

2. By combining different 3D entities, i.e. contour

and surface information, higher precision and ro-

bustness in pose estimates can be achieved.

The paper is structured as follows. In Sect. 2 we

describe the feature extraction process. In Sect. 3,

we describe how the object representation is obtained.

Sect. 4 describes how model-scene correspondences

are obtained, and Sect. 5 how the estimation process

is performed. Finally, experiments provide an evalua-

tion of our process in Sects. 6 and 7.

105

Glent Buch A., Kraft D., Kämäräinen J. and Krüger N..

Pose Estimation using a Hierarchical 3D Representation of Contours and Surfaces.

DOI: 10.5220/0004275801050111

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 105-111

ISBN: 978-989-8565-47-1

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Pose estimates using contour features only, sur-

face features only and the combination of both. Top: a

frontal training stereo view used for generating a model.

The input view (bottom) is rotated 35

◦

compared to the

training view. The trained model points are shown in blue

(contours) and red (surﬂings). White points represent the

matched points in the input. The error is given as the ground

truth translation error. Left: Fit using only contours. Mid-

dle: Fit using only surfaces. Right: Fit using both kinds of

features.

1.1 Related Work

In the domain of 3D object alignment, a signiﬁcant

amount of research has been done. Methods based on

local descriptors have proven to be usable in resolving

correspondences between a stored model and a scene

in a stable manner. Many of these works involve 2D

descriptors (see e.g. (Bay et al., 2006; Belongie et al.,

2002; Lowe, 1999)). Since these methods do not need

any kind of 3D data, they can be directly applied to

monocular images. In general, for these methods the

accuracy of the pose estimate is limited since rather

signiﬁcant pose changes in 3D might result in only

small changes in the projected image.

A notable work using 3D entities is (Johnson and

Hebert, 1999) where descriptors are formed as spin

images which act essentially as a sub-sampling of the

shape information in the neighborhood of a surface

point. In a previous work (Stein and Medioni, 1992),

a splash descriptor is formed by the differential prop-

erties of the neighborhood. An interesting descrip-

tor is presented in (Bariya and Nishino, 2010; Novat-

nack and Nishino, 2008) where focus lies on scale-

dependent keypoint features providing rich shape in-

formation. In (Hetzel et al., 2001; Rusu et al., 2009),

local geometric descriptors are formed by histograms

of relative coordinate frames for capturing local char-

acteristics of the object. Some of the most convincing

results, however, have been reported based on very

local point pair representations (Drost et al., 2010;

Papazov and Burschka, 2010; Wahl et al., 2003) in

which the density of the full model representation is

utilized. In (Payet and Todorovic, 2011), contours are

used in a framework for monocular-based object de-

tection. Instead of a context descriptor, a summary

descriptor is generated on a lattice in the image.

All the methods mentioned above operate on geo-

metric information only on one scale and one kind of

descriptor without making use of any relational infor-

mation in 3D. In our approach we make use of the

different granularities in the visual hierarchy, show

the complementary role of surface and contour infor-

mation and apply viewpoint invariant relational fea-

ture descriptors. In addition, our method includes

appearance information by incorporating appropriate

descriptors.

The concept of using context information derives

from (Belongie et al., 2002; Frome et al., 2004) in

which such context information is encoded by deﬁn-

ing a 2D or 3D neighborhood around a point. The

difference to our approach is that the distal properties

encoded are not restricted to the spatial domain but

also apply to appearance attributes, and that we op-

erate on two kinds of descriptors at the same time on

different levels of granularity.

2 ECV SCENE

REPRESENTATION

The foundation of our work lies in the way 3D entities

are obtained given a stereo image pair. We make use

of an early cognitive vision (ECV) system described

in (Jensen et al., 2010; Pugeault et al., 2010), which

provides a processing hierarchy from the lowest level

(pixels) to increasingly higher level of abstraction (see

Figure 2).

The system ﬁrst performs linear image ﬁltering

operations for the extraction of 2D primitives, here

line segments and textured regions (texlets). Cor-

respondences between left and right image are then

searched for, and the line segments and texlets are re-

constructed in 3D. The result of this is a relatively

dense 3D scene representation in both the contour

and the surface domain containing line segments and

texlets. We refer to these entities as primitives. The

line segments are deﬁned by position, direction and

color, and texlets by a position, normal vector and

mean color. These 3D primitives can be grouped,

which results in higher-level entities, or simply fea-

tures, which we call contours and surﬂings. A contour

thus consists of a set of line segments with similar di-

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

106

Figure 2: Example of an ECV interpretation of a scene.

rection and color. Similarly, a surﬂing is made up of a

group of texlets with similar normal vector direction

and color. The grouping has a smoothing effect which

increases robustness of the generated features, even

under large viewpoint transformations. The ECV rep-

resentation of an example scene is shown in Figure 2.

3 ECV CONTEXT DESCRIPTORS

The result of the ECV processing presented in Sect. 2

is a scene representation consisting of a sparse set of

features with a high descriptive ability. These features

capture the object geometry and appearance in differ-

ent ways. Contours reﬂect distance and orientation

discontinuities as well as color borders. Surﬂings are

able to describe the local appearance of a surface. At

the current stage, we generate a training stereo image

based on a textured CAD model from which we ex-

tract the 3D feature set. This process could also be

done using views of real objects captured in an exper-

iment setup.

To obtain an even higher level of descriptive abil-

ity, we calculate relations between a feature and all

other features in a local spatial region. Inspired by

(Belongie et al., 2002; Frome et al., 2004), we refer

to the complete set of relations of a given feature as

a context. An object model thus consists of a set of

features and their contexts. The locality of a context

is controlled by a radius given as a distance in Eu-

clidean space. In contrast to many existing methods,

our context descriptors also include appearance infor-

mation. Figure 3 shows the whole processing pipeline

from input image to 2D primitives to 3D features (left

part), and ﬁnally to the context of a feature using a

Figure 3: ECV representation of the KIT object “Blue-

SaltCube” and an example of a surﬂing context descriptor.

Top part: left input image from rendered stereo image, ex-

tracted 2D primitives (line segments and texlets) and recon-

structed 3D contours and surﬂings (contours not shown by

intrinsic color, but using a unique color label). Bottom part:

an example context based on set of relations of a surﬂing

with a radius of 25 mm. Relation parameter distributions

shown by histograms.

radius of 25 mm (right part). The ﬁve histograms of

the context descriptor show the sampled distribution

of the relations to the neighboring features in terms of

geometry (angle and distance) as well as appearance

(RGB color differences). The object is taken from the

Karlsruhe Institute of Technology (KIT) database of

household objects (KIT, ), which is also used for the

experiments presented in Sect. 6.

As previously mentioned, we extract context in-

formation both in the model building phase as well

as in the execution phase. As the features represent

different visual modalities (Kr

uger et al., 2004), the

parametrization also differs. We list the relational fea-

ture parameters in Table 1. Contours are denoted by

C and surﬂings by S.

Table 1: Parameters of the different relation types for con-

tours C and surﬂings S.

Name Relation types Parameters

Angle C ↔ C, S ↔ S R

Distance C ↔ C, C ↔ S, S ↔ S R

Color difference C ↔ C, C ↔ S, S ↔ S R

Distances are calculated using the center points of

the features. For surﬂings, the angle is simply de-

PoseEstimationusingaHierarchical3DRepresentationofContoursandSurfaces

107

ﬁned as the dihedral angle. For contours, we perform

a principal component analysis on the contour line

segments and take the eigenvector corresponding to

the largest eigenvalue to get the main direction. This

direction vector is then used for calculating angle dif-

ferences. In Figure 4, we show how these spatial re-

lations are obtained.

Figure 4: Spatial relations for a contour pair (left) and a sur-

ﬂing pair (right). This ﬁgure also shows the line segments

making up a contour as well as the texlets making up a sur-

ﬂing.

The context descriptor D of a feature F ∈ {C, S}

is deﬁned as the complete set of feature relations R ∈

} in a neighborhood bounded by the radius

D(F ) = {R (F ,F

) | R

(F ,F

) < r} (1)

where F

is any other feature in the neighborhood. A

complete object/scene model, M and S , is thus ex-

tracted from the total set of descriptors, which we de-

note as:

M = {D

} (2)

S = {D

} (3)

4 CORRESPONDENCES

We perform a correspondence search between the

model M and the scene descriptors S in order to

eliminate scene features not expected to be part of

the model sought. This operation can be regarded

as a ﬁltering which removes scene entities which do

not match the model features according to some met-

ric. This metric is deﬁned in Sect. 4.1 where we ex-

plain the feature matching. In Sects. 4.2 and 4.3, we

show how this information is used for resolving cor-

respondences. While the correspondence matching in

Sect. 4.1 is done on entities extracted on higher lev-

els of the visual hierarchy (i.e. contours and surﬂings)

and their contexts, the actual computation of the pose

is done based on the local primitives which the higher

level entities consist of (i.e. 3D line segments and

texlets). Sect. 5 describes how the ﬁnal pose estima-

tion is done based on the remaining set of putative

feature correspondences between the model and the

scene.

4.1 Matching

For the relations in Table 1, we deﬁne a discrete func-

tion ξ ∈ {C ↔ C,C ↔ S, S ↔ S} for a given relation

R which enumerates the possible combinations of en-

tity pairs or relation types. This is done to assure that

only alike relations are compared. It would not make

sense to match e.g. a relation of type C ↔ C against a

relation of type C ↔ S.

Given the context descriptors of two features of

the same type, we perform matching using the follow-

ing cost function based on mean absolute differences:

c(D

) =

∑

∈D

min

∈D

: ξ(R

)=ξ(R

)}

abs(R

− R

)

(4)

where | ·| denotes the cardinality of a set. The term in-

side the sum calculates for each relation in the model

descriptor the “distance” to the nearest matching rela-

tion in the scene descriptor. This can also be regarded

as a local assignment using closest point matching

measured by absolute differences. Since the differ-

ent parameters have different ranges, we normalize

all parameters and thereby the cost c to the interval

[0,1]. Fortunately, all parameters except distances are

intrinsically bounded (e.g. angles are bounded to the

range [0, 90]

◦

). For the distance parameter, we simply

normalize using r since this represents the maximally

possible distance deviation between two relations.

4.2 Feature Assignment

To establish correspondences between a model and a

scene, we calculate all descriptors D

of the scene and

compare them to the model descriptors D

using (4).

We form an unbalanced weighted bipartite graph G =

(U,V,E) where



. Each edge is

labeled by c(D

). Clearly, edges can only be

drawn between features of the same type which makes

the graph incomplete.

To solve the assignment, we generate a cost ma-

trix of dimension |U | × |V | of all the edge labels. We

then apply the Hungarian method (Kuhn, 1955) which

produces a global minimum matching, i.e. a one-to-

one matching h between the model and the scene that

minimizes the following:

∑

∈M

c(D

,h(D

)) (5)

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

108

To remove outliers in this matching, we discard as-

signments with a cost larger than a predetermined

threshold ε

. The result is an injection h : M → S con-

taining putative feature correspondences for a subset

of the model features.

4.3 Point Correspondence Assignment

As will be clear from the following section, we need

3D correspondences between points in order to gen-

erate and validate pose hypotheses of the rigid ob-

ject transformation. This problem has been partially

solved by the feature assignment described in the pre-

vious section. However, taking only the center point

of the individual features provides too little informa-

tion of the object geometry for the pose estimation

step. We therefore exploit the fact that features are

the result of a grouping of lower-level point entities,

i.e. 3D line segments and texlets (see Figure 2). Since

the correspondence search relates each model feature

to one scene feature, we can transfer this knowledge

to the point entities simply by setting all points in the

corresponding scene feature as putative correspon-

dences of a point in the model feature. This choice

is based on the following observation: when a feature

assignment is performed, it is based on spatial and

appearance invariants. This does not give us any in-

formation of the absolute placement of the point enti-

ties making up the feature. Line segments and texlets

can thus ﬂoat around freely under different viewing

conditions. In other words, we do not know how the

individual line segments/texlets of a contour/surﬂing

are ordered under different viewing conditions since

we do not know the object pose yet. We only know

that the features correspond, so all line segment/texlet

points inside a scene contour/surﬂing can be potential

matches of each line segment/texlet point inside the

model contour/surﬂing.

Based on this, we end up with a one-to-many re-

lationship between the model/scene points which we

denote P and Q respectively. The point correspon-

dences are stored as a |P |× |Q | index or match matrix

M. In the pose estimation step, we ultimately seek a

bijection between the two sets, relating each model

point to one scene point.

5 POSE ESTIMATION

The pose estimation strategy puts all the previously

mentioned methods together in a strategy for obtain-

ing an object pose from 3D scene data. The input to

the algorithm is a previously generated context model

of an object and extracted 3D features of a scene. The

following steps are performed:

1. From 3D scene feature data, extract all feature re-

lations and thereby contexts with context radius

2. For all model features, match the context descrip-

tor up against each scene feature context using (4).

• If the cost c to the closest scene feature falls

below a threshold ε

, store the feature pair as a

putative feature correspondence.

3. Derive one to many point correspondences and

store the indexed matches in the matrix M.

• Contours: for each line segment point along

the model contour, store all line segment points

along the matched scene contour as putative

point correspondences.

• Surﬂings: for each texlet point on a model

surﬂing, store all texlet points on the matched

scene surﬂing as putative point correspon-

dences.

4. Find the pose estimate from the set of putative

point correspondences that gives the best ﬁt of the

model in the scene using RANSAC (Fischler and

Bolles, 1981).

• In the sampling stage, we start by sampling

three model points randomly from P . For each

of these, we sample a correspondence from

the putative correspondence subset of Q en-

coded in the match matrix M. To obtain a

pose hypothesis, we apply Umeyama’s method

(Umeyama, 1991).

• In the veriﬁcation stage, we use the median

Euclidean distance between the transformed

model and scene points to get a more robust es-

timation. This is referred to as the ﬁt error.

This strategy assures a robust search for point corre-

spondences between the model and the scene as well

as high accuracy in the resulting pose estimate.

6 RESULTS

We have performed extensive evaluation of our algo-

rithm using the KIT database (KIT, ) which at the cur-

rent stage consists of 112 textured objects. For each

object, we generate eight 45

◦

-spaced training views of

the object to cover the whole object. Then we rotate

the object with an increment of 5

◦

away from each

training view to generate input images. We thus eval-

uate each view up against eight rotations. In Figure 5,

we show example images for ﬁve different objects.

PoseEstimationusingaHierarchical3DRepresentationofContoursandSurfaces

109

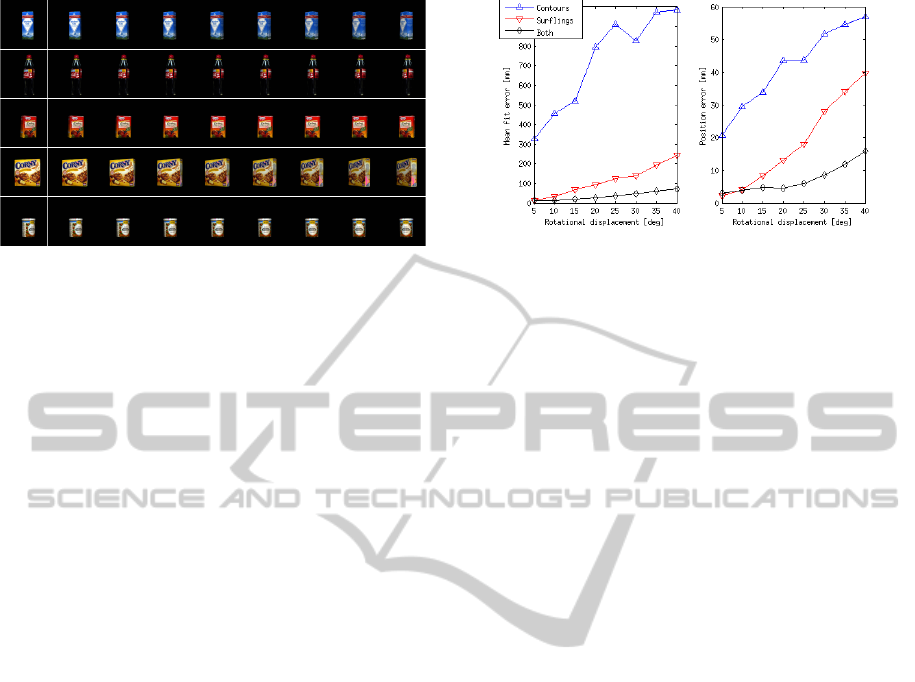
Figure 5: Example training images and test sequences (left

view only) for ﬁve different objects in the database. In the

leftmost column, the training images are shown, and on the

right side of the vertical white line, the test images corre-

sponding to the rotations {5

◦

,10

◦

,. . . , 40

◦

} away from the

training image are shown. Artifacts stem from the database

and were caused by imperfect scans.

Note that only one training case out of eight is shown

for each object.

As this is done in simulation using the textured

CAD model, we can compare our results with ground

truth and get an absolute error measure this way. An

instance of an alignment is visualized in Figure 1,

where we show these errors for contours only, sur-

ﬂings only and both.

In the experiments we set the context radius to

r = 25 mm. This parameter should always reﬂect a

compromise between descriptive ability and robust-

ness towards occlusions. We have found this value to

be a good compromise. For RANSAC, we set an up-

per bound of 500 iterations. In Figure 6 we show both

the ﬁt errors (left) and the ground truth errors (right)

of the experiments for all views of all objects.

As the ground truth errors reveal, we achieve

alignment errors well below 0.5 cm for rotation up

to 20

◦

and signiﬁcantly below 2 cm even under large

rotations up to 40

◦

when combining the feature types.

Pose estimation on contours alone produces on av-

erage worse results than matching based on surface

information. However, for non-textured objects con-

taining contour information this is in general the only

information available when visual stereo is used. Pose

estimation algorithms based on texture information

only would fail completely in that case. As shown

in Figure 6, the combination of surface and con-

tour information improves performance signiﬁcantly.

Hence, the experiments show that contours are an

important source of information for pose estimation,

even for textured objects.

Figure 6: Estimation results for all textured KIT objects.

Left: mean of all ﬁt errors. Right: mean of all ground truth

errors.

7 CONCLUSIONS

We have described a pose estimation algorithm which

makes use of viewpoint invariant representations in

terms of context descriptors organized in a visual hier-

archy covering two parallel streams, one correspond-

ing to contour structures and the other to texture struc-

tures. We have made quantitative evaluations on a

data set of 112 objects for which the ground truth is

known. We have shown that the combination of con-

tour and surface information increases the accuracy of

pose estimation, keeping the ground truth error mag-

nitudes below the errors in the estimation using only

contour or surface information.

ACKNOWLEDGEMENTS

The research leading to these results has received

funding from the European Community’s Seventh

Framework Programme FP7/2007-2013 (Speciﬁc

Programme Cooperation, Theme 3, Information and

Communication Technologies) under grant agree-

ment no. 269959, IntellAct.

REFERENCES

KIT ObjectModels Web Database http://i61p109.ira.uka.de/

ObjectModelsWebUI.

Bariya, P. and Nishino, K. (2010). Scale-hierarchical 3D

object recognition in cluttered scenes. In Computer

Vision and Pattern Recognition (CVPR), 2010 IEEE

Conference on, pages 1657 –1664.

Bay, H., Tuytelaars, T., and Gool, L. V. (2006). Surf:

Speeded up robust features. In Proceedings of the

ninth European Conference on Computer Vision.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

110

Belongie, S., Malik, J., and Puzicha, J. (2002). Shape

matching and object recognition using shape con-

texts. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 24(4):509 –522.

Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model

globally, match locally: Efﬁcient and robust 3D object

recognition. In Computer Vision and Pattern Recog-

nition (CVPR), 2010 IEEE Conference on, pages 998

–1005.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Commun. ACM, 24(6):381–395.

Frome, A., Huber, D., Kolluri, R., Bulow, T., and Malik,

J. (2004). Recognizing objects in range data using

regional point descriptors. In Proceedings of the Eu-

ropean Conference on Computer Vision (ECCV).

Hetzel, G., Leibe, B., Levi, P., and Schiele, B. (2001). 3D

object recognition from range images using local fea-

ture histograms. In Proceedings of the 2001 IEEE

Computer Society Conference on Computer Vision

and Pattern Recognition (CVPR)., volume 2, pages

394–399.

Jensen, L., Kjær-Nielsen, A., Pauwels, K., Jessen, J.,

Van Hulle, M., and Krger, N. (2010). A two-level

real-time vision machine combining coarse- and ﬁne-

grained parallelism. Journal of Real-Time Image Pro-

cessing, 5:291–304. 10.1007/s11554-010-0159-4.

Johnson, A. and Hebert, M. (1999). Using spin im-

ages for efﬁcient object recognition in cluttered 3D

scenes. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 21(5):433 –449.

uger, N., Felsberg, M., and W

org

otter, F. (2004).

Processing multi-modal primitives from image se-

quences. Fourth International ICSC Symposium on

Engineering of Intelligent Systems.

Kuhn, H. W. (1955). The hungarian method for the assign-

ment problem. Naval Research Logistics Quarterly,

2(1-2):83–97.

Lowe, D. (1999). Object recognition from local scale-

invariant features. In Computer Vision, 1999. The Pro-

ceedings of the Seventh IEEE International Confer-

ence on, volume 2, pages 1150 –1157 vol.2.

Novatnack, J. and Nishino, K. (2008). Scale-

dependent/invariant local 3D shape descriptors

for fully automatic registration of multiple sets of

range images. In Proceedings of the 10th European

Conference on Computer Vision: Part III, ECCV ’08,

pages 440–453, Berlin, Heidelberg. Springer-Verlag.

Papazov, C. and Burschka, D. (2010). An efﬁcient ransac

for 3D object recognition in noisy and occluded

scenes. In Proceedings of the 10th Asian Conference

on Computer Vision, pages 135–148. Springer-Verlag.

Payet, N. and Todorovic, S. (2011). From contours to 3D

object detection and pose estimation. In Computer Vi-

sion (ICCV), 2011 IEEE International Conference on,

pages 983 –990.

Pugeault, N., W

org

otter, F., and Kr

uger, N. (2010). Visual

primitives: Local, condensed, and semantically rich

visual descriptors and their applications in robotics.

International Journal of Humanoid Robotics (Special

Issue on Cognitive Humanoid Vision), 7(3):379–405.

Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point

feature histograms (FPFH) for 3D registration. In

Robotics and Automation, 2009. ICRA ’09. IEEE In-

ternational Conference on, pages 3212 –3217.

Stein, F. and Medioni, G. (1992). Structural indexing:

Efﬁcient 3-D object recognition. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

14(2):125 –145.

Umeyama, S. (1991). Least-squares estimation of transfor-

mation parameters between two point patterns. Pat-

tern Analysis and Machine Intelligence, IEEE Trans-

actions on, 13(4):376 –380.

Wahl, E., Hillenbrand, U., and Hirzinger, G. (2003). Surﬂet-

pair-relation histograms: a statistical 3D-shape repre-

sentation for rapid classiﬁcation. In 3-D Digital Imag-

ing and Modeling, 2003. 3DIM 2003. Proceedings.

Fourth International Conference on, pages 474 –481.

PoseEstimationusingaHierarchical3DRepresentationofContoursandSurfaces

111