
Three Dimensional Packing Algorithm
with Consideration of Loading and Unloading Order
Naoki Kobatake, Hidenori Ohta and Mario Nakamori
Department of Information and Computer Sciences,
Faculty of Engineering, Tokyo University of Agriculture and Technology, Koganei, Tokyo, Japan
Keywords: 3-Dimensional Packing, Re-Packing, The Order of Loading and Unloading.
Abstract: A novel packing problem for truck or containership transportation is considered. A truck or a ship visits
several accumulation places in a delivery tour, and items are loaded or unloaded at each accumulation place.
In order to carry items as many as possible at one delivery tour, we often have to unpack and repack some
items even at nondestination places if they blockade loading other items. Such packing and repacking,
however, will make the transportation cost increase. Thus, a packing that requirs smaller number of
unpacking and repacking is desired. In this paper, we extend the slicing-tree which is a method of a
representation of packing and propose an algorithm to pack items into the container with minimum the
number of unpacking and re-packing.
1 INTRODUCTION
From the viewpoint of reducing the cost of
transportation by truck or containership, it is desired
to carry as many items as possible at one delivery.
Developing a plan of loading items into a container
is often considered as “the rectangular solid packing
problem,” i.e., to allocate small rectangular solids
without overlapping in a big rectangular empty box,
and there have been published many papers on the
rectangular solid packing problem (S. D. Allen et al.,
2011), (G. Fuellerer et al., 2010), (H. Kawashima et
al., 2010), (F. K. Miyazawa, and Y. Wakabayashi,
2009), and (H. Ohta et al., 2008) .
In practice, we often have to take care about the
order of items loading and unloading when we
develop a loading plan. For example, suppose that a
ship or a truck visits several accumulation places in
a delivery tour, and items are loaded or unloaded at
each accumulation place. In such a case, the loading
and unloading order of items is subject to the order
of visiting the accumulation places, which is
difficult to be changed without changing the delivery
routing. There are, however, few preceding studies
about the packing problem where the order of both
loading and unloading is given.
Moreover, even if we consider only about either
loading or unloading, the packing problem is still
difficult. That is because, if we put each item in the
rear side of the container in the order of loading (or
the inverse order of unloading), all items may not be
put in the container.
Therefore, we should permit to unload
temporarily an item if it blockades other items
loading (unloading), and after the loading
(unloading), to reload the blockading item again into
the container. Hereafter we call such unloading of
blocking items unpacking and such reloading
repacking. Since repacking causes
increase of cost,
we should pack the items in the container so that
fewer items are to be repacked.
In this paper, we discuss the above packing
problem where the order of both loading and
unloading is given. An effective algorithm to put the
items with the minimum number of repacking is
proposed and its performance will be shown by
computational experiments.
2 DEFINITION OF THE
PROBLEM
In this paper, we assume that items are rectangular
solids and the container is also rectangular placed
along x-axis, y-axis and z-axis in three-dimensional
Euclidean space. The direction from left [resp. front,
top] to right [back, bottom] is viewed as the x[y, z]-
116
Kobatake N., Ohta H. and Nakamori M..
Three Dimensional Packing Algorithm with Consideration of Loading and Unloading Order.
DOI: 10.5220/0004277502640269
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 264-269
ISBN: 978-989-8565-40-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
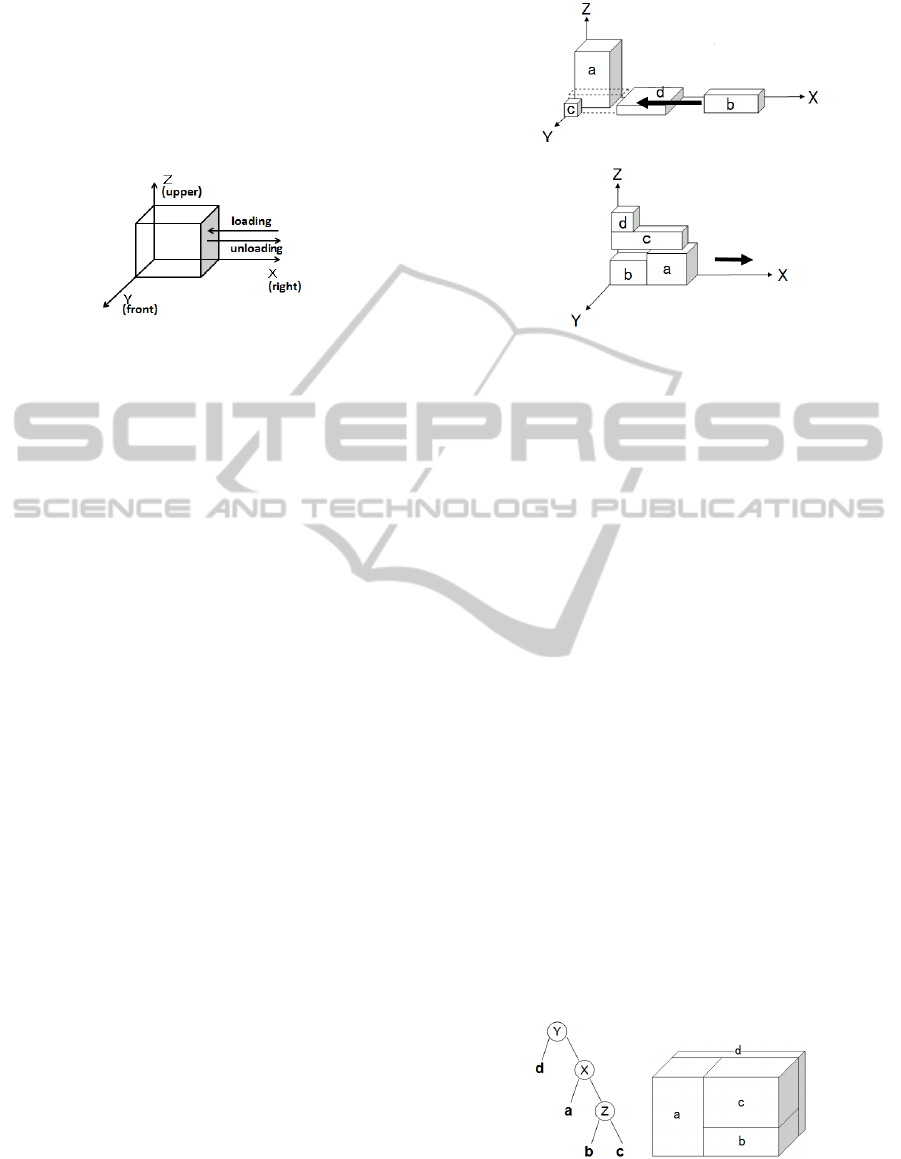
direction. The door of the container is located at the
right side. Figure 1 shows an aspect of the container
and directions of loading and unloading of items.
Centers of gravity of the items are out of
consideration in this paper, i.e., any allocations of
the items are permitted unless items overlap with
other items or walls of the container.
Figure 1: Container and direction of loading and unloading.
The loading and the unloading clock time are
already given for each item. In accordance with the
clock times, we obtain a partial order of loading and
unloading. In the process of an item loading
(unloading), other items which have been already
located in the container may blockade the loading
(unloading). In this case, we unload the items, which
we call “blocking items,” from the container. After
loading (unloading) of the item, we re-pack the
blocking items into the original position.
Now, we discuss the locations of the blocking
items when an item is loaded to or unloaded from
the container. When the item a is loaded into the
container, the locations of the blocking items are on
the left of or the upper of the place where the
loading item a is to be located. In this paper, if the
item b satisfies both of the following two conditions,
then b is defined as the blocking item against the
item a loading:
(i) After loading of the item a, the front face of the
item a is located in the front side of the rear face of
the item b, and the rear face of the item a is located
in the rear side of the front face of the item b;
(ii) After loading of the item a, both of the following
two conditions are satisfied:
(ii-1) The right face of the item a locates in left side
of the left face of the item b, and the bottom face of
the item a is lower than upper face of the item b:
(ii-2) The upper face of the item a is lower than the
bottom face of the item b, and the left face of the
item a locates in left side of the right face of the item
b.
Figure 2 (a) shows that the item d blocks when
the item b is loaded, where the space in which the
item b is to be located is represented by broken lines.
Item d has to be unloaded first and then be repacked
after the loading of the item b. Thus, the number of
repacking is one.
(a)
(b)
Figure 2: Blocking items against loading and unloading.
The blocking item against the item unloading is
also defined similarly. Figure 2 (b) shows that the
item c blocks when the item a is unloaded. Item c
has to be unloaded, but the item d blocks unloading
of the item c. Therefore the item c has to be also
unloaded and then to be repacked after the unloading
of the item a. Thus, the number of repacking is two.
The purpose of this paper is to propose an
algorithm of packing items into a container so that
the number of re-packing is the minimum.
3 THREE-DIMENSIONAL
SLICING-TREE
A rectangular solid dissection, which is a dissection
of a rectangular solid region into smaller rectangular
solids (rooms) by places
is often used to represent a
packing. That is,
items are assigned to the distinct
rooms (any two items do not share a single room). In
particular, a structure of a rectangular solid
dissection which is obtained by recursively cutting
by planes
perpendicular to x, y or z-axis is called
three-dimensional slicing-structure. Figure 3(a)
shows a three-dimensional slicing-structure.
(a) (b)
Figure 3: Three-dimensional slicing structure and the
corresponding slicing-tree.
ThreeDimensionalPackingAlgorithmwithConsiderationofLoadingandUnloadingOrder
117

A three-dimensional slicing-structure can be
represented by a binary tree, where internal nodes
and external nodes correspond to planes and rooms
respectively. In particular, the internal nodes are
classified into “X-nodes”, “Y-nodes” and “Z-nodes”.
X-nodes [resp. Y-nodes, Z-nodes] correspond to the
planes
perpendicular to x-axis [y-axis, z-axis] in the
rectangular solid dissection. The left subtree of the
X-node [resp. Y-node, Z-node] corresponds to the
leftward [frontward, upward] region of the
corresponding plane, and the right subtree of the X-
node [resp. Y-node, Z-node] corresponds to the
rightward [backward, downward] region of the
corresponding plane. The slicing tree does not allow
the representation of all packings, However the near
optimal packing can be modeled. Figure 3(b) shows
the slicing-tree which is the representation of the
slicing-structure shown in figure 3(a).
It is obvious that a region which corresponds to
an external node must be larger than the item. In
addition, the shape of each region which
corresponds to a subtree is a rectangular solid. Now
we express the size of rectangular solid A as
(
A
X
A
Y
A
Z
), where
A
X
[resp.
A
Y
,
A
Z
] is the
x[y, z]-length of the rectangular solid A. Assume the
size of the rectangular solid which corresponds to
the left subtree of a X-node P is (
L
X
L
Y
L
Z
),
the size of the rectangular solid which corresponds
to the right subtree of P is (
R
X
R
Y
R
Z ) and
the size of the rectangular solid which corresponds
to the subtree which is merged the trees and whose
root is P is (
P
X
P
Y
P
Z ) respectively. Then we
have the following inequalities.
RLP
XXX
,
),max(
RLP
YYY ,
),max(
RLP
ZZZ
In the case where P is Y-node or Z-node, similar
inequalities are also satisfied. The properties mean
that we can decode the slicing-tree into the
corresponding packing by the post order traverse of
the tree in O(n) time, where n is the number of items
(L. Cheng et al., 2004).
If the size of the rectangular solid which
corresponds to the entire slicing-tree is smaller than
the size of the container, every item can be located
into the container and the packing is feasible.
4 PROPOSED ALGORITHM
We extend the three-dimensional slicing-tree to
represent placement, loading and unloading of the
items. Using the extended representation, we search
for a packing that minimizes the number of re-
packing with simulated annealing. The search of
item placement consists of two phases. In Phase 1,
every item are put into the container. In Phase 2, the
number of re-packing is minimized.
4.1 Extension of Slicing-Tree
For any two items, if one is unloaded earlier than the
loading of the other, they never overlap with each
other. So these two items can be located into the
same place in the container. To represent the above
placement of two items, we introduce "T nodes" as
internal nodes of the slicing-tree. The meaning is
that any two items, which correspond to the external
nodes on the left and right subtree of the T-node
respectively, do not exist in a container at the same
time. Figure 4(a) shows an original three-
dimensional slicing-tree, and Figure 4(b) shows a
proposed slicing-tree which is obtained by
introducing T node into the slicing-tree shown in
Figure 4(a). Note that the clock time of loading and
unloading are set and each external node stores the
times. Figure 5 (a) and (b) show the placement of
items which is represented by the slice tree shown in
Figure 4(b).
(a) (b)
Figure 4: Introduction of T node to slicing-tree.
We can check whether any X(Y, Z) node in the
original slicing-tree can be changed to T-node by
comparing "clock times of loading of items in the
right subtree" and "clock times of unloading of items
in the left subtree". Therefore, we obtain the
extended slicing-tree by the original slicing-tree in
O(n) time.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
118
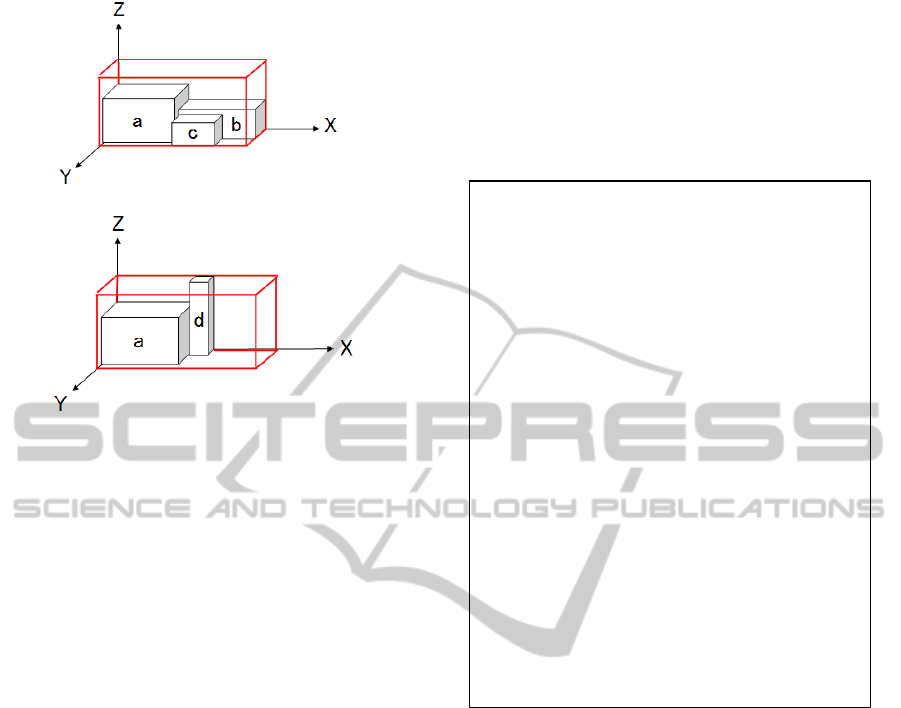
(a) Placement of items when time clock is 4
(b) Placement of items when time clock is 8
Figure 5: Placement of items corresponding to slicing-tree
shown in Figure 4 (b).
If the size of the rectangular solid which
corresponds to the left subtree of a T-node P is
(
L
X
L
Y
L
Z
), the size of the rectangular solid
which corresponds to the right subtree of P is
(
R
X
R
Y
R
Z
), and the size of rectangular solid
which corresponds to the subtree whose root is P is
(
P
X
P
Y
P
Z
) respectively, then the following
inequalities are satisfied.
),max(
RLP
XXX ,
),max(
RLP
YYY
,
),max(
RLP
ZZZ .
4.1.1 Counting the Number of Re-Packings
Using an extended slicing-tree, we can count the
number of re-packing of the placement of items. For
any pair of items a and b, the following necessary
conditio
ns are satisfied if b will block to a loading:
(i) The type of a least common ancestor of a and b is
X-node or Z-node;
(ii) a is contained in the left subtree of the least
common ancestor ;
(iii) When a is loaded into the container, b is located
in the container.
We can count the number of re-packing by using
above conditions in O(n
2
) time. However, since the
conditions are not a sufficient condition, we may
overestimate, if we count only by using the
conditions. Such overestimate can be detected by
considering the positional relation between a and b.
Thus, we present an algorithm to count the number
of re-packing by the proposed slicing-tree. The
running time of the algorithm is O(n
2
t), where t is
the number of clocking time when items are loaded
or unloaded.
4.2 Phase 1
In Phase 1, we don’t evaluate the number of re-
packings but evaluate the size of a rectangular solid
corresponding to the entire extended slice-tree to see
whether all items can be located into the container or
not.
An objective function of simulated annealing
search is the x-length of a rectangular solid
corresponding to the extended slice-tree. In addition,
if the y-length or z-length is larger than that of the
container, a penalty proportional to the surplus is
added to the cost function.
We search by using the original slicing-tree (The
tree does not include the T-node), and obtain the
extended slicing-tree for the evaluation. The initial
solution is that the items are laid out on the line.
Figure 6 (a) shows the placement of items in the
initial solution, Figure 6 (b) shows the
corresponding slicing-tree.
I
nput: extended slicing-tree
Output: N_r (the number of re-packing
for items loading)
Count_repacking (extended slicing-tree)
{
N_r = 0;
for(each clock time
t
){
for(each node n in post-order traverse of the
extended slicing-tree){
calculate num_of_blocked(
n,t
);
}
N_r = N_r + num_of_blocked(root of the extended
slicing-tree
,t
);
}
return N_r;
}
num_of_blocked(node
n,
clock time
t
)
{
if (node n is an external node){
check the positional relation between n and each item
if (when the clock time is
t
, there exists at least
one item whose loading is blocked by
n
) return 1;
else return 0;
}
else
return( num_of_blocked(left child of
n
,
t
)
+ num_of_blocked(right child of
n
,
t
)) ;
}
ThreeDimensionalPackingAlgorithmwithConsiderationofLoadingandUnloadingOrder
119
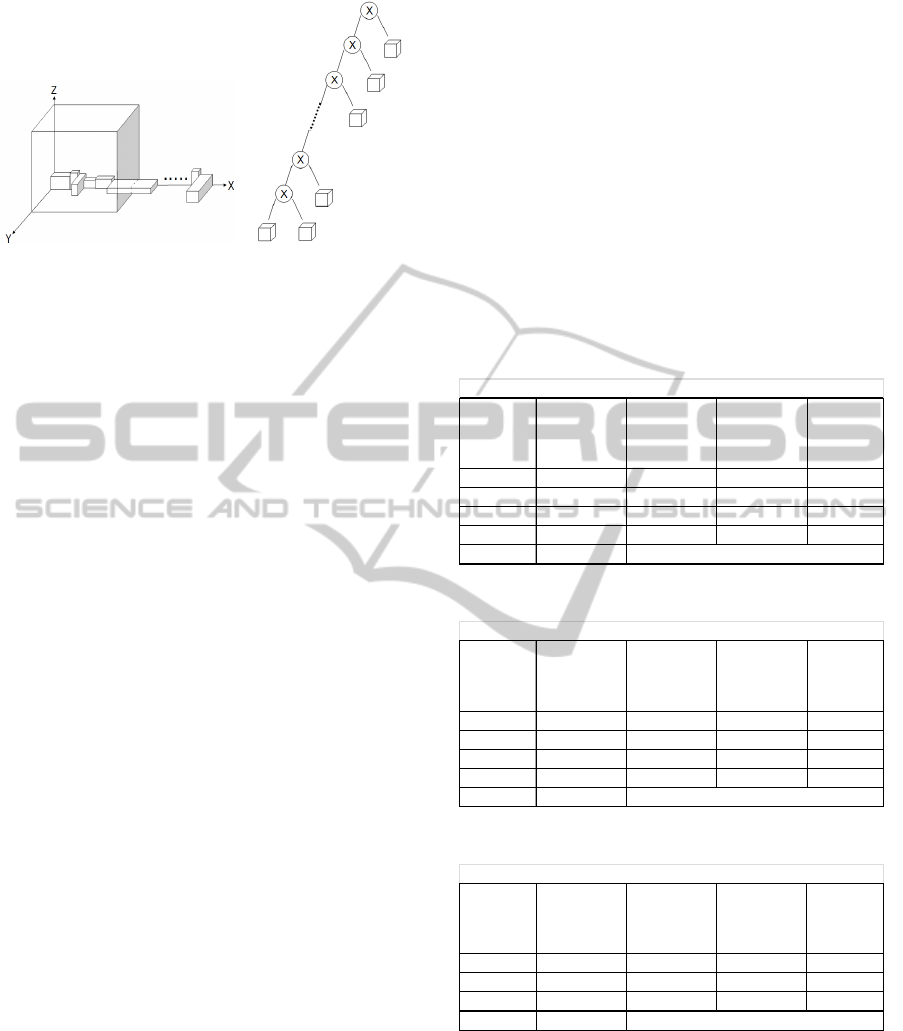
(a) (b)
Figure 6: Initial placement of items and corresponding
slicing-tree.
The neighbourhood solution is obtained by one
of the following four operations:
(a)Rotation of the item: One item is chosen at
random, and the direction of the item is changed;
(b)Exchange of subtrees: Two subtrees are chosen at
random, and exchanged with each other, if the sub-
trees do not contain each other;
(c)Exchange of items: Two external nodes are
chosen at random and are exchanged with each
other;
(d)Transposition of placement: an internal node is
chosen at random and its type (X-node, Y-node or
Z-node) is changed.
4.3 Phase 2
In Phase 2, we evaluate the number of re-packings
and minimize it. During the search, if a
neighbourhood solution is infeasible, the solution is
rejected and new neighbourhood solution is created.
The initial solution of the search is the result of
searching in Phase 1. The neighbourhood solution is
obtained by using the above four operations.
5 COMPUTER EXPERIMENTS
We carried out an experiment on a computer to
evaluate the performance of the proposed method.
The computer environment is an Intel Core i7-200
3.40 GHz CPU with 2 GB of memory. The
programming language used is C.
The instances for the experiment were made at
random. The number of items is 20, 30 or 50. The
length of each side of the items is 10 through 30.
The loading clock time and unloading clock time of
each item are 1 through 10. Several sets of
containers of different size are made. The ratio of
length along x, y, and z axis of a container is 5:2:3,
which reflects the side ratio of real trucks.
The results of the experiments are shown in table
1, 2 and 3. These results show that we obtain small
number of re-packings except in one instance.
Time_Phase1 is the average of the time until all
items be located into the container. We almost
obtained feasible solutions in a practical time. But
the increase of the packing ratio or the number of
items makes it difficult to gain the feasible solutions,
and we failed loading in some instances. To solve
them, we need more flexible re-packing.
Time_Phase2 is the average of the time until the
convergence of the search.
Table 1: Experiment results (20 items).
total
packing
ratio(%)
maximum
packing
ratio(%)
time_Phase1
(sec.)
time_Phase2
(sec.)
number of
re-
packings
64.80 34.15 0 2310 0
87.50 46.10 1 1167 2
122.16 64.37 1 1167 2
146.52 77.21 1546 113 21
177.82 93.70
20 items
loading failure
Table 2: Experiment results (30 items).
total
packing
ratio(%)
maximum
packing
ratio(%)
time_Phase1
(sec.)
time_Phase2
(sec.)
number of
re-
packings
79.46 43.31 2 23542 0
91.99 50.13 2 24161 3
107.29 58.47 3 23877 4
126.18 68.77 134 48683 10
149.79 81.63
30 items
loading failure
Table 3: Experiment results (50 items).
total
packing
ratio(%)
maximum
packing
ratio(%)
time_Phase1
(sec.)
time_Phase2
(sec.)
number of
re-
packings
86.89 44.26 53 11318 4
100.91 51.40 48 58699 4
118.17 60.19 491 550445 4
150.14 76.48
50 items
loading failure
In particular, we will show the detail of the result
of one of our instances. The instance has 30 items
whose length of each side is 10 through 30. The size
of the container is (90
36
54). The maximum
packing ratio is 68.77%, and the ratio of the sum of
volume of all items to the volume of the container
(total packing ratio) is 126.18%.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
120
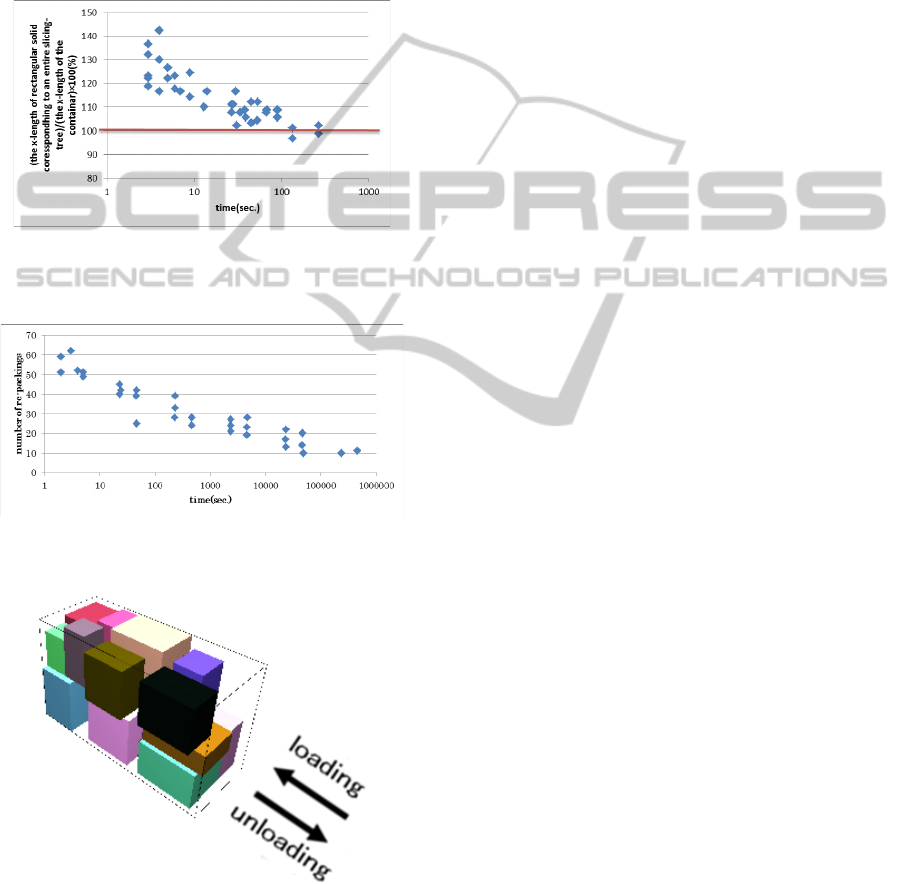
Figure 7 shows the result in the Phase 1, that is
the relation between the length of the rectangular
solid corresponding to the extended slicing-tree and
the searching time.
Figure 8 shows the relation between the number
of re-packings and the searching time.
Figure 9 shows the result of placement of items
when the packing ration is the maximum (68.77%).
The number of repacking of the placement is 10.
Figure 7: Relation between the length of the rectangular
solid corresponding to the extended slicing-tree and the
searching time.
Figure 8: Relation between the number of re-packing and
the searching time.
Figure 9: Placement of items when the packing ratio is the
maximum.
6 CONCLUSIONS
In this paper, we described a novel packing problem
which is the order of loading and unloading of items
is given and proposed an algorithm that minimizes
the number of repacking. Further works are as
follows:
(i) More flexible re-packing: when an item is
repacked, we would like to allow that the item is put
on arbitrary position in the container, i.e., the
position different from the position which the item
was unloaded from;
(ii) Application to a more practical case: we should
consider about a center of gravity of the items and
packaging materials.
REFERENCES
S. D. Allen et al., 2011. A hybrid placement strategy for
the three-dimensional strip packing problem, European
Journal of Operational Research, Vol. 209, pp.219-227.
L. Cheng et al., 2004, Floorplan Design for 3-D ICs, Proc.
SASIMI, pp.395-401.
G. Fuellerer et al., 2010. Metaheuristics for vehicle routing
problems with three-dimensional loading constraints,
European Journal of Operational Research, Vol. 201,
pp.751-759.
H. Kawashima et al., 2010, An efficient implementation of
a constructive algorithm for the three-dimensional
packing problem, Forum of Information Technology
2010 (FIT2010) Vol. 1,pp.31-38.
F. K. Miyazawa, and Y. Wakabayashi, 2009, "Three-
dimensional packings with rotations," Computers &
Operations Research, Vol. 36, pp.2801-2815.
H. Ohta et al., 2008. The O-Sequence: Representation of
3D-Dissection, IEICE Transactions on Fundamentals
of Electronics, Communications and Computer
Sciences, Vol. E91-A, pp.2111-2119.
ThreeDimensionalPackingAlgorithmwithConsiderationofLoadingandUnloadingOrder
121
