
TriSI: A Distinctive Local Surface Descriptor for 3D Modeling
and Object Recognition
Yulan Guo
1,2
, Ferdous Sohel
2
, Mohammed Bennamoun
2
, Min Lu
1
and Jianwei Wan
1
1
College of Electronic Science and Engineering, National University of Defense Technology, Changsha, P.R.China
2
School of Computer Science and Software Engineering, The University of Western Australia, Perth, Australia
Keywords:
Local Surface Descriptor, 3D Modeling, 3D Object Recognition, Range Image Registration.
Abstract:
Local surface description is a critical stage for surface matching. This paper presents a highly distinctive local
surface descriptor, namely TriSI. From a keypoint, we first construct a unique and repeatable local reference
frame (LRF) using all the points lying on the local surface. We then generate three spin images from the three
coordinate axes of the LRF. These spin images are concatenated and further compressed into a TriSI descriptor
using the principal component analysis technique. We tested our TriSI descriptor on the Bologna Dataset
and compared it to several existing methods. Experimental results show that TriSI outperformed existing
methods under all levels of noise and varying mesh resolutions. The TriSI was further tested to demonstrate
its effectiveness in 3D modeling. Experimental results show that it can accurately perform pairwise and
multiview range image registration. We finally used the TriSI descriptor for 3D object recognition. The results
on the UWA Dataset show that TriSI outperformed the state-of-the-art methods including spin image, tensor
and exponential map. The TriSI based method achieved a high recognition rate of 98.4%.
1 INTRODUCTION
Surface matching is a fundamental research topic in
both 3D Computer Vision and Computer Graphics. It
has a number of applications, including 3D modeling
(Mian et al., 2006), 3D shape retrieval (Shilane et al.,
2004), 3D object recognition (Attene et al., 2011; Guo
et al., 2012; Guo et al., 2013), 3D mapping (Huber
et al., 2000), robotics (Lai et al., 2011b), and reverse
engineering(Williams and Bennamoun, 2000). With
the rapid development of low-cost 3D scanners (e.g.,
Microsoft Kinect), range images are becoming more
available (Lai et al., 2011a; Rusu and Cousins, 2011).
The data availability together with the progress in
high-speed computing devices have increased the de-
mand for efficient and accurate range image represen-
tation techniques (Mian et al., 2010).
There are two basic approaches to represent a
range image, namely global feature and local feature
based approaches (Salti et al., 2011). A global fea-
ture based approach uses a global feature to represent
a surface. It is very popular in 3D shape retrieval, but
it is sensitive to occlusion and clutter. A local feature
based approach however, uses a set of 3D keypoints
and local surface descriptors to represent a surface. It
is therefore, suitable to surface matching in the pres-
ence of occlusion and clutter (Salti et al., 2011). In
the process of surface matching, the distinctiveness
and robustness of the local surface descriptors play a
significant role (Taati and Greenspan, 2011).
A number of papers on local surface descriptors
can be found in the literature (Bustos et al., 2005;
Bronstein et al., 2010; Boyer et al., 2011). Chua and
Jarvis (1997) proposed a Point Signature by record-
ing the signed distances between the neighboring sur-
face points and their correspondences in a fitted plane.
Point Signature is however, sensitive to noise and
varying mesh resolutions (Mian et al., 2005). Johnson
and Hebert (1999) proposed a Spin Image descriptor
by accumulating the neighboring points into a 2D his-
togram. The spin image is one of the most cited meth-
ods in the literature. It is however weakly distinc-
tive and sensitive to varying mesh resolutions (Mian
et al., 2010). Chen and Bhanu (2007) used Local Sur-
face Patches (LSP) to represent a range image. Since
the LSP descriptor requires the calculation of second-
order derivatives of a surface, it is sensitive to noise.
Flint et al. (2007) introduced the THRIFT descriptor
by generating a 1D histogram according to the surface
normal deviations. Tombari et al. (2010) proposed
a Signature of Histograms of OrienTations (SHOT)
by encoding the surface normal deviations in a parti-
86
Guo Y., Sohel F., Bennamoun M., Lu M. and Wan J..
TriSI: A Distinctive Local Surface Descriptor for 3D Modeling and Object Recognition.
DOI: 10.5220/0004277600860093
In Proceedings of the International Conference on Computer Graphics Theory and Applications and International Conference on Information
Visualization Theory and Applications (GRAPP-2013), pages 86-93
ISBN: 978-989-8565-46-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

tioned spherical neighborhood. The SHOT is highly
descriptive. It is however, also sensitive to varying
mesh resolutions. Other descriptors include Point’s
Fingerprint (Sun and Abidi, 2001), 3D Shape Context
(Frome et al., 2004), Tensor (Mian et al., 2006), Ex-
ponential Map (EM) (Novatnack and Nishino, 2008)
and Variable-Dimensional Local Shape Descriptors
(VD-LSD) (Taati and Greenspan, 2011).
Most of the existing local surface descriptors suf-
fer from low descriptiveness, or robustness to noise,
or sensitivity to varying mesh resolutions (Bariya
et al., 2012). Motivated by these limitations, we
propose a highly distinctive and robust local surface
descriptor called Tri-Spin-Image (TriSI). The TriSI
is an improvement of the Spin Image descriptor. It
first builds a unique and repeatable Local Reference
Frame (LRF) for each keypoint. It then generates
three spin images by spinning one sheet around each
axis of the LRF. The three images are concatenated to
form an overall TriSI descriptor. The TriSI descrip-
tor is further compressed using the Principal Compo-
nent Analysis (PCA) technique. Performance evalu-
ation results show that our proposed TriSI descriptor
is highly descriptive. It is very robust to both noise
and varying mesh resolutions. The effectiveness of
TriSI descriptor was also demonstrated by 3D mod-
eling including pairwise and multiview range image
registration. The TriSI descriptor was further used for
3D object recognition and was tested on the UWA
Dataset. Experimental results show that TriSI out-
performed the state-of-the-art methods including Spin
Image, Tensor, EM and VD-LSD.
The rest of this paper is organized as follows: Sec-
tion 2 describes the TriSI surface descriptor. Section
3 presents the feature matching performance. Section
4 demonstrates the TriSI based 3D modeling meth-
ods and their experimental results. Section 5 presents
the 3D object recognition results. Section 6 concludes
this paper.
2 TriSI SURFACE DESCRIPTOR
The process of generating a TriSI surface descriptor
includes three modules, i.e., LRF construction, TriSI
generation and TriSI compression.
2.1 LRF Construction
Given a triangular mesh surface S and a set of key-
points {o
o
o
1
,o
o
o
2
,··· , o
o
o
K
}, a set of local surface descrip-
tors { f
f
f
1
, f
f
f
2
,··· , f
f
f
K
} should be generated to repre-
sent the surface S . Here, K denotes the number of
keypoints on the surface S . For a given keypoint
o
o
o
k
,k = 1, 2,··· ,K, we first extract the local surface
L using a sphere of radius r centered at o
o
o
k
. We then
construct a LRF for o
o
o
k
using all the points lying on
the local surface L rather than using just the mesh
vertices.
Assume that the local surface L contains N trian-
gles and M vertices. For the ith triangle with vertices
q
q
q
i1
, q
q
q
i2
and q
q
q
i3
, we calculate the scatter matrix S
i
us-
ing the continuous PCA algorithm:
S
i
=
1
12
3
∑
j=1
3
∑
n=1
q
q
q
ij
− o
o
o
k
(q
q
q
in
− o
o
o
k
)
T
+
1
12
3
∑
j=1
q
q
q
ij
− o
o
o
k
q
q
q
ij
− o
o
o
k
T
. (1)
The overall scatter matrix S of the local surface L
is then calculated as:
S =
N
∑
i=1
γ
i1
γ
i2
S
i
, (2)
where the weights γ
i1
and γ
i2
are respectively defined
as:
γ
i1
=
|(q
q
q
i2
− q
q
q
i1
) × (q
q
q
i3
− q
q
q
i1
)|
∑
N
i=1
|(q
q
q
i2
− q
q
q
i1
) × (q
q
q
i3
− q
q
q
i1
)|
, (3)
γ
i2
=
r−
o
o
o
k
−
q
q
q
i1
+ q
q
q
i2
+ q
q
q
i3
3
2
. (4)
We perform an eigenvalue decomposition on the
scatter matrix S to get three orthogonal eigenvectors
v
v
v
1
, v
v
v
2
and v
v
v
3
. These eigenvectors are in the order
of decreasing magnitude of their associated eigenval-
ues. The eigenvectors v
v
v
1
, v
v
v
2
and v
v
v
3
form the basis
for the LRF. However, their directions are ambigu-
ous. That is, −v
v
v
1
, −v
v
v
2
and −v
v
v
3
are also eigenvectors
of the scatter matrix S. We therefore propose a sign
disambiguation technique.
We define the unambiguous vectors
e
v
v
v
1
and
e
v
v
v
3
as:
e
v
v
v
1
= v
v
v
1
· sgn
N
∑
i=1
γ
i1
γ
i2
3
∑
j=1
q
q
q
ij
− o
o
o
k
v
v
v
1
!!
, (5)
e
v
v
v
3
= v
v
v
3
· sgn
N
∑
i=1
γ
i1
γ
i2
3
∑
j=1
q
q
q
ij
− o
o
o
k
v
v
v
3
!!
, (6)
where sgn(·) denotes the signum function that ex-
tracts the sign of a real number. Vector
e
v
v
v
2
is then
defined as
e
v
v
v
3
×
e
v
v
v
1
.
Finally, we construct a LRF for the keypoint o
o
o
k
using o
o
o
k
as the origin and the unambiguous vectors
{
e
v
v
v
1
,
e
v
v
v
2
,
e
v
v
v
3
} as the three coordinate axes.
TriSI:ADistinctiveLocalSurfaceDescriptorfor3DModelingandObjectRecognition
87
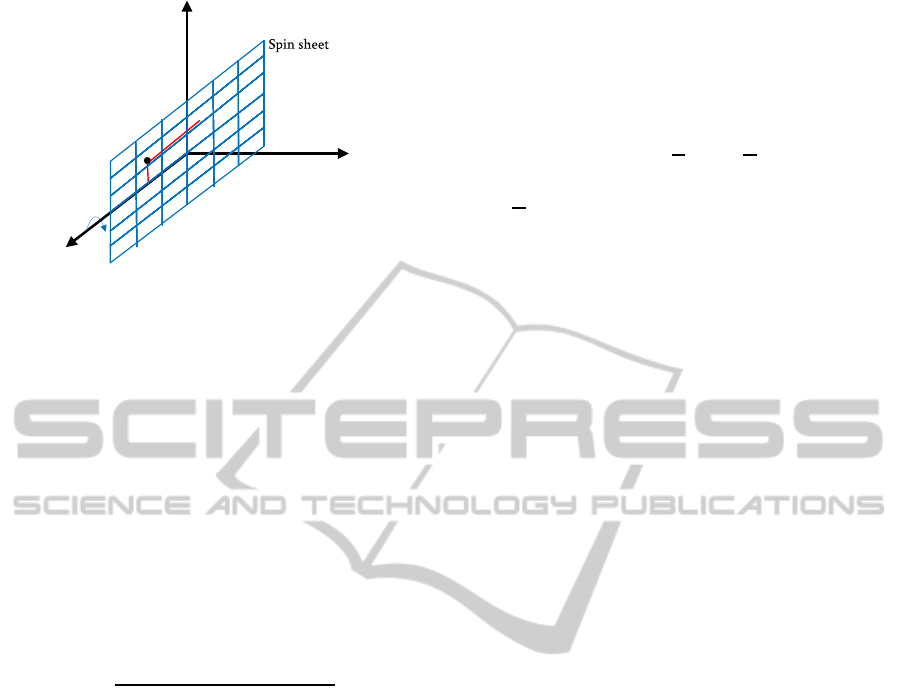
q
α
β
1
%
v
2
%
v
3
%
v
k
o
Figure 1: An illustration of the generation of a spin image.
(Figure best seen in color.)
2.2 TriSI Generation
Given a keypoint o
o
o
k
, the local surface L and the LRF
vectors {
e
v
v
v
1
,
e
v
v
v
2
,
e
v
v
v
3
}, we generate three spin images
{SI
1
,SI
2
,SI
3
} by respectively spinning a sheet about
the three axes of the LRF.
We first generate a spin image by spinning a sheet
about the
e
v
v
v
1
axis. An illustration is shown in Fig. 1.
Given the LRF, each point q
q
q on the local surface L is
represented by two parameters α and β. Here, α is the
perpendiculardistance of q
q
q from the line which passes
through o
o
o
k
and is parallel to
e
v
v
v
1
. β is the signed per-
pendicular distance to the plane which goes through
o
o
o
k
and is perpendicular to
e
v
v
v
1
, that is:
α =
q
kq
q
q− o
o
o
k
k
2
− (
e
v
v
v
1
· (q
q
q− o
o
o
k
))
2
, (7)
β =
e
v
v
v
1
· (q
q
q− o
o
o
k
). (8)
We accumulate the parameters (α,β) of all the
points on L into a B × B histogram, where B is the
number of bins along each dimension of the his-
togram. We further bilinearly interpolate this 2D his-
togram to account for noise. The interpolated his-
togram is our improved spin image SI
1
.
We then generate two other spin images SI
2
and
SI
3
by following the exact same way we adopted to
generate SI
1
. That is, SI
2
and SI
3
are generated by
substituting the
e
v
v
v
1
in Equations (7-8) with
e
v
v
v
2
and
e
v
v
v
3
,
respectively. We finally concatenate the three spin im-
ages to obtain our TriSI descriptor, that is:
TriSI = {SI
1
,SI
2
,SI
3
}. (9)
2.3 TriSI Compression
The dimensionality of the TriSI descriptor is 3B
2
, and
it is therefore too large for an efficient feature match-
ing. For example, if B is set to be 15, the dimension-
ality of a TriSI is 675. We therefore project the TriSI
to a PCA subspace to get a more compact feature de-
scriptor. The PCA subspace can be learned from a set
of training descriptors { f
f
f
1
, f
f
f
2
,··· , f
f
f
T
}, where T is
the number of training descriptors. We calculate the
scatter matrix M as:
M =
T
∑
i=1
f
f
f
i
− f
f
f
f
f
f
i
− f
f
f
T
, (10)
where f
f
f is the mean vector of all these training de-
scriptors.
We then perform an eigenvalue decomposition on
M:
MV = VD, (11)
where D is a diagonal matrix with diagonal entries
equal to the eigenvalue of M, V is a matrix with
columns equal to the eigenvectors of M.
We define the PCA subspace using the eigenvec-
tors corresponding to the highest n eigenvalues. The
value of n is chosen such that 95% of the fidelity is
preserved in the compressed data.
Therefore, the compressed vector
b
f
f
f
i
of a feature
descriptor f
f
f
i
is:
b
f
f
f
i
= V
T
n
f
f
f
i
, (12)
where V
T
n
is the transpose of the first n columns of V.
During feature matching, we use the Euclidean
distance to measure the distance between any two de-
scriptors
b
f
f
f
i
and
c
f
f
f
j
.
3 FEATURE MATCHING
PERFORMANCE
We tested the performance of TriSI descriptor on
the Bologna Dataset (Tombari et al., 2010). We
also compared it with several state-of-the-art descrip-
tors including Spin Image (SpinIm) (Johnson and
Hebert, 1999), Normal Histogram (NormHist) (Het-
zel et al., 2001), Local Surface Patches (LSP) (Chen
and Bhanu, 2007) and SHOT (Tombari et al., 2010).
The experimental results are presented in this section.
3.1 Experimental Setup
The Bologna Dataset (Tombari et al., 2010) contains
six models and 45 scenes. The models were taken
from the Stanford 3D Scanning Repository (Curless
and Levoy, 1996). The scenes were generated by ran-
domly placing different subsets of the models in order
to create clutter and pose variances. The ground-truth
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
88

Table 1: Tuned parameter settings for five feature descrip-
tors.
Support Radius (mr) Dimensionality Length
SpinIm 15 15*15 225
NormHist 15 15*15 225
LSP 15 15*15 225
SHOT 15 8*2*2*10 320
TriSI 15 29*1 29
transformations between each model and its instances
in the scenes were provided in the dataset.
We adopt the frequently used Recall vs 1-
Precision Curve (RP Curve) (Ke and Sukthankar,
2004) to measure the performance of a feature de-
scriptor. If the distance between a scene feature de-
scriptor and a model feature descriptor is smaller than
a threshold τ, this pair of feature descriptors is consid-
ered a match. Further, if the two feature descriptors
come from the same physical location, this match is
considered a true positive. Otherwise, it is considered
a false positive. Given the total number of positives as
a priori, the recall and 1-precision are calculated, as in
(Ke and Sukthankar,2004).A RP Curve can therefore,
be generated by varying the threshold τ.
We first randomly selected a set of keypoints from
each model (1000 keypoints in our case), and ob-
tained their corresponding points from the scene. We
then used a feature description method (e.g., TriSI) to
extract a set of feature descriptors. The scene feature
descriptors were finally matched against the model
feature descriptors to produce a RP Curve. The pa-
rameters for all the five feature description methods
were tuned by a Tuning Dataset which contains the
six models and their transformed versions (obtained
by resampling to
1
/2 of their original mesh resolution
and adding 0.1mr Gaussian Noise). Note that, ‘mr’
denotes the average mesh resolution of the six mod-
els, which is used as the unit for metric parameters.
We also trained the PCA subspace using the TriSI de-
scriptors of the six models. The tuned parameter set-
tings for all feature descriptors are shown in Table 1.
3.2 Robustness to Noise
In order to test performance of all these descriptors
in the presence of noise, we added different levels of
noise with standard deviations of 0.1mr, 0.3mr, and
0.5mr to the 45 scenes. We generated one RP Curve
for a feature descriptor at each noise level. The RP
Curves of these five descriptors are shown in Fig. 2.
It can be observed that our TriSI descriptor
achieved the best performance at all levels of noise,
while SHOT achieved the second best performance.
The performance of all these descriptors decreased
as the level of noise increased from 0.1mr to 0.5mr.
However, our TriSI was more robust to noise com-
pared to the others. It obtained a high recall of about
0.7 together with a high precision of about 0.7 even
with a high level noise (with a deviation of 0.5mr),
which is shown in Fig. 2(c). Moreover, the gap be-
tween SHOT and TriSI got larger when level of noise
increased. This validated the strong robustness and
consistency of our TriSI descriptor in the presence of
noise.
It can also be observed that NormHist and SpinIm
performed well under a low level of noise (with a de-
viation of 0.1 mr), as shown in Fig. 2(a). They how-
ever, failed to work when a medium level of noise
(with a deviation of 0.3mr) was added, as shown
in Fig. 2(b). This is because the generation of a
NormHist or a SpinIm requiressurface normals which
are very sensitive to noise. In contrast, LSP was
highly susceptible to noise. It achieved a very low
recall and precision even under a low level of noise
(with a deviation of 0.1mr), as shown in Fig. 2(a).
This is mainly due to the reason that LSP is based on
the shape index values of the local surface which are
even more sensitive to noise compared to surface nor-
mals.
3.3 Robustness to Varying Mesh
Resolutions
In order to test the performance of these descriptors
with respect to varying mesh resolutions, we resam-
pled the noise-free scenes down to
1
/2,
1
/4 and
1
/8 of
their original mesh resolution. We generated one RP
Curve for a feature descriptor at each level of mesh
decimation. The RP Curves of these descriptors are
shown in Fig. 3.
It was found that our TriSI was very robust to
varying mesh resolutions, and outperformed the other
descriptors by a large margin under all levels of mesh
decimation. TriSI achieved a high recall of about 0.95
under
1
/2 mesh decimation, as shown in Fig. 3(a). It
also achieved a recall of about 0.9 under
1
/4 mesh dec-
imation, as shown in Fig. 3(b). TriSI consistently
achieved a good performance even under
1
/8 mesh
decimation, with a recall of more than 0.8, as shown
in Fig. 3(c). It is worth noting that the performance
of TriSI under
1
/8 mesh decimation was even better
than the performance of SpinIm under
1
/2 mesh deci-
mation, as shown in Figures 3(a) and (c). This clearly
justifies the effectiveness and robustness of the TriSI
descriptor with respect to varying mesh resolutions.
Moreover, our TriSI descriptor is very compact.
As shown in Table 1, the length of a compressed TriSI
in this experiment is only 29. In contrast, the second
TriSI:ADistinctiveLocalSurfaceDescriptorfor3DModelingandObjectRecognition
89

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.80.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
11
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(a)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 11
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
11
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(b)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 11
0
0.1
0.2
0.3
0.4
0.5
0.6
0.70.7
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(c)
Figure 2: Recall vs 1- precesion curves in the presence of noise. (a) Noise with a deviation of 0.1mr. (b) Noise with a deviation
of 0.3mr. (c) Noise with a deviation of 0.5mr.
0 0.1 0.2 0.3 0.4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
11
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(a)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.80.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
11
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(b)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.80.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
11
1−Precision
Recall
SpinIm
NormHist
LSP
SHOT
TriSI
(c)
Figure 3: Recall vs 1- precision curves with respect to varying mesh resolutions. (a)
1
/2 mesh decimation. (b)
1
/4 mesh
decimation. (c)
1
/8 mesh decimation.
shortest length of the other descriptors is 225, which
is larger than the length of TriSI by an order of magni-
tude. This means that our TriSI can be matched more
efficiently compared to the other methods.
4 3D MODELING
In order to demonstrate the effectiveness of TriSI for
3D modeling, we used TriSI to perform pairwise and
multiview range image registration.
4.1 Pairwise Range Image Registration
Given a pair of range images {S
1
,S
2
} of an object,
we respectively generate a set of TriSI descriptors for
both S
1
and S
2
. We match the TriSI descriptors of S
1
against the TriSI descriptors of S
2
to obtain a set of
feature correspondences {C
1
,C
2
,··· ,C
N
c
}, where N
c
is the number of feature correspondences. For each
feature correspondence C
i
, we can generate a trans-
formation (R
i
,t
t
t
i
) between S
1
and S
2
using the LRFs
and the point positions. That is, the rotation matrix R
i
and translation vector t
t
t
i
are calculated as follows:
R
i
= F
T
s1i
F
s2i
, (13)
t
t
t
i
= o
o
o
s1i
− o
o
o
s2i
R, (14)
where o
o
o
s1i
and o
o
o
s2i
are respectively the positions of
the corresponding points from S
1
and S
2
, F
s1i
and F
s2i
are respectively the LRFs of o
o
o
s1i
and o
o
o
s2i
.
We calculate a total of N
c
transformations from
the N
c
feature correspondences. These transforma-
tions are then grouped into a few clusters. Each clus-
ter center gives a potential transformation between S
1
and S
2
. We sort these clusters based on their sizes
and their average feature distances. We verify several
most likely transformations and choose the transfor-
mation which produce the least registration error be-
tween S
1
and S
2
.
We applied our TriSI based pairwise range image
registration method to two range images of the Chef
model of the UWA Dataset (Mian et al., 2006). Fig.
4(a) shows the feature matching results between the
two range images. It is clear that the majority of fea-
ture matches are true positives. This feature matching
result further indicates the high descriptiveness of our
TriSI descriptor. Although there are a few false posi-
tives in the feature matching result, they can easily be
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
90

(a) (b)
Figure 4: Pairwise range image registration results. (a) Feature matching result between two range images of the Chef. (b)
Pairwise registration result. (Figure best seen in color.)
(a) (b) (c)
Figure 5: Multiview range image registration result. (a) Initial set of 22 range images of the Chef model. (b) Coarse registra-
tion result by TriSI based method. (c) The fine 3D model in the UWA Dataset. (Figure best seen in color.)
eliminated by the process of grouping. As shown in
Fig 4(b), the alignment between the two range images
are very accurate.
4.2 Multiview Range Image
Registration
Given a set of range images {S
1
,S
2
,··· ,S
N
r
} of an
object, we generate a set of TriSI descriptors for each
range image. Once the TriSI descriptors are obtained,
we use a tree based algorithm to perform multiview
range image registration. We first select the range im-
age S
i
which has the maximum surface area as the
root node of the tree. We then use the aforementioned
pairwise registration method to match S
i
with the re-
maining range images in the search space. Once a
range image S
j
is accurately registered with S
i
, the
range image S
j
is added to the tree as a new node
and removed from the search space. The arc between
the two nodes represents the rigid transformation be-
tween S
j
and S
i
. Once all range images have been
matched with S
i
, the algorithm proceeds to the next
node. This process continues until all range images in
the search space are added to the tree. Once the tree is
fully constructed, the transformation between any two
connected nodes is already available. Based on these
estimated transformations, we transform all range im-
ages to the coordinate basis of the range image at the
root node. These multiview range images can there-
fore be aligned without any manual intervention.
We applied our TriSI based multiview range im-
age registration method to 22 range images of the
Chef model of the UWA Dataset. Fig. 5(a) shows the
initial set of range images, and Fig. 5(b) illustrates
our registration result. It is clear that our TriSI based
method achieved a highly accurate alignment without
use of any priori information (e.g., the image order
or initial pose of each image). A visual comparison
between the coarse registered range images and the
original fine 3D model shows that the registration re-
sult is almost identical to the original model, as shown
in Figures 5 (b) and (c). This result further demon-
strates the effectiveness of our TriSI based method.
It is expected that the registration results can further
be improved by using a global registration algorithm,
e.g., (Williams and Bennamoun, 2001).
TriSI:ADistinctiveLocalSurfaceDescriptorfor3DModelingandObjectRecognition
91
5 OBJECT RECOGNITION
To further evaluate the performance of our TriSI de-
scriptor, we used TriSI to perform 3D object recogni-
tion on the UWA Dataset (Mian et al., 2006). The
UWA Dataset is one of the most frequently used
datasets. It contains five models and 50 real scenes.
Our 3D object recognition algorithm goes through
two phases: offline pre-processing and online recog-
nition. During the offline pre-processing phase, we
extract our TriSI descriptors from a set of randomly
selected keypoints from all models. We also index
these TriSI descriptors using a k-d tree structure for
efficient feature matching. During the online recogni-
tion phase, we first extract TriSI descriptors from a set
of randomly selected keypoints in a given scene. We
then match the scene descriptors against the model
descriptors using the k-d tree. The feature matching
results are used to vote for candidate models and to
generate transformation hypotheses. The candidate
models are then verified in turn by aligning them with
the scene using a transformation hypothesis. If the
candidate model is aligned accurately with a portion
of the scene, the candidate model and transforma-
tion hypothesis are accepted. Subsequently, the scene
points that correspond to this model are recognized
and segmented. Otherwise, the transformation hy-
pothesis is rejected and the next hypothesis is verified
by turn.
We conducted our experiments using the same
data and experimental setup as in (Mian et al., 2006)
and (Bariya et al., 2012) to achievea rigorous compar-
ison. The recognition rates of our TriSI based method
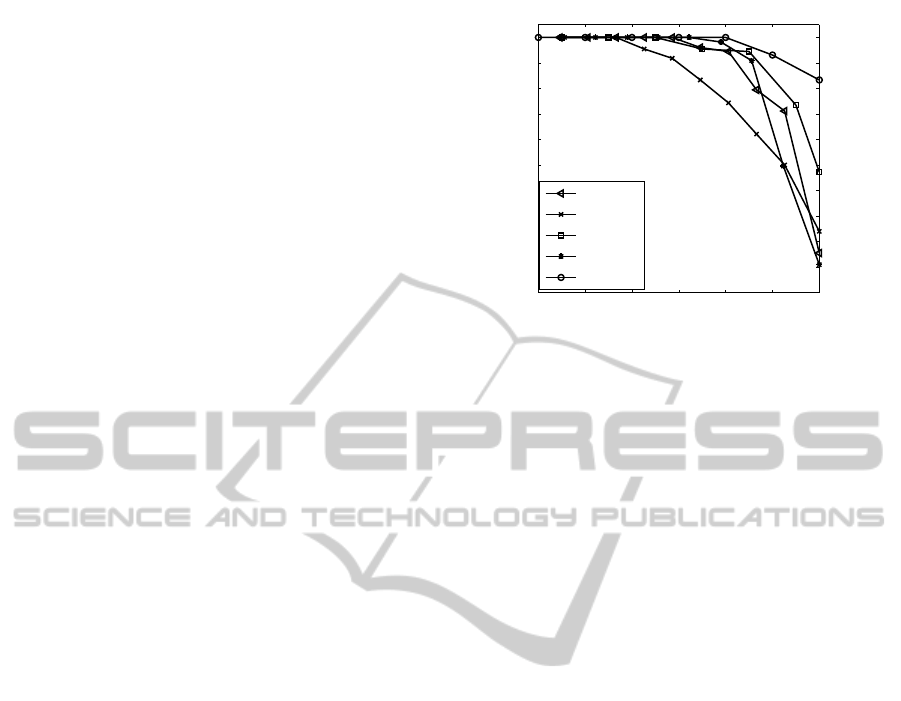
are shown in Fig. 6 with respect to varying levels
of occlusion. We also present the recognition results
of Tensor (Mian et al., 2006), SpinIm (Mian et al.,
2006), VD-LSD (Taati and Greenspan, 2011) and EM
(Bariya et al., 2012) based methods.
As shown in Fig. 6, our method achieved the best
recognition results. The average recognition rate of
our TriSI based methods was 98.4%. That is, only
three out of the 188 objects in the 50 scenes were
not correctly recognized. The second best results
were produced by EM based method with an aver-
age recognition rate of 97.5%. They were followed
by Tensor, VD-LSD and SpinIm based methods.
Our TriSI based method is also robust to occlu-
sion. It achieved a 100% recognition rate under upto
80% occlusion. As occlusion further increased, the
recognition rate decreased slightly. It obtained a
recognition rate of more than 80% even under 90%
occlusion. In contrast, the second best recognition
rate under 90% occlusion was only about 50%, which
was reported by the EM based method.
60 65 70 75 80 85 90
0
10
20
30
40
50
60
70
80
90
100
Occlusion (%)
Recognition rate (%)
Tensor
SpinIm
EM
VD−LSD
TriSI
Figure 6: Recognition rates on the UWA Dataset.
6 CONCLUSIONS
In this paper, we presented a distinctive TriSI local
descriptor. We evaluated the descriptiveness and ro-
bustness of our TriSI descriptor with respect to dif-
ferent levels of noise and mesh resolutions. Experi-
mental results show that TriSI is very robust to noise
and varying mesh resolutions. It outperformed all
existing method. We also used our TriSI descriptor
for both pairwise and multiview range image regis-
tration. TriSI achieved highly accurate registration
results. Moreover, we used TriSI based method to
perform 3D object recognition. Experimental results
revealed that our method achieved the best recogni-
tion rate. Overall, our TriSI based method is robust
to noise, occlusion and varying mesh resolutions. It
outperformed the state-of-the-art methods.
ACKNOWLEDGEMENTS
This research is supported by a China Scholar-
ship Council (CSC) scholarship (2011611067) and
Australian Research Council grants (DE120102960,
DP110102166).
REFERENCES
Attene, M., Marini, S., Spagnuolo, M., and Falcidieno, B.
(2011). Part-in-whole 3D shape matching and dock-
ing. The Visual Computer, 27(11):991–1004.
Bariya, P., Novatnack, J., Schwartz, G., and Nishino, K.
(2012). 3D geometric scale variability in range im-
ages: Features and descriptors. International Journal
of Computer Vision, 99(2):232–255.
Boyer, E., Bronstein, A., Bronstein, M., Bustos, B., Darom,
T., Horaud, R., Hotz, I., Keller, Y., Keustermans, J.,
GRAPP2013-InternationalConferenceonComputerGraphicsTheoryandApplications
92

Kovnatsky, A., et al. (2011). SHREC 2011: Robust
feature detection and description benchmark. In Euro-
graphics Workshop on Shape Retrieval, pages 79–86.
Bronstein, A., Bronstein, M., Bustos, B., Castellani, U.,
Crisani, M., Falcidieno, B., Guibas, L., Kokkinos, I.,
Murino, V., Ovsjanikov, M., et al. (2010). SHREC
2010: robust feature detection and description bench-
mark. In Eurographics Workshop on 3D Object Re-
trieval, volume 2, page 6.
Bustos, B., Keim, D., Saupe, D., Schreck, T., and Vrani´c, D.
(2005). Feature-based similarity search in 3D object
databases. ACM Computing Surveys, 37(4):345–387.
Chen, H. and Bhanu, B. (2007). 3D free-form object recog-
nition in range images using local surface patches.
Pattern Recognition Letters, 28(10):1252–1262.
Curless, B. and Levoy, M. (1996). A volumetric method
for building complex models from range images. In
23rd Annual Conference on Computer Graphics and
Interactive Techniques, pages 303–312.
Frome, A., Huber, D., Kolluri, R., B¨ulow, T., and Malik, J.
(2004). Recognizing objects in range data using re-
gional point descriptors. In 8th European Conference
on Computer Vision, pages 224–237.
Guo, Y., Bennamoun, M., Sohel, F., Wan, J., and Lu, M.
(2013). 3D free form object recognition using rota-
tional projection statistics. In IEEE 14th Workshop on
the Applications of Computer Vision. In press.
Guo, Y., Wan, J., Lu, M., and Niu, W. (2012).
A parts-based method for articulated tar-
get recognition in laser radar data. Optik.
http://dx.doi.org/10.1016/j.ijleo.2012.08.035.
Hetzel, G., Leibe, B., Levi, P., and Schiele, B. (2001). 3D
object recognition from range images using local fea-
ture histograms. In IEEE Conference on Computer
Vision and Pattern Recognition, volume 2, pages II–
394.
Huber, D., Carmichael, O., and Hebert, M. (2000). 3D map
reconstruction from range data. In IEEE International
Conference on Robotics and Automation, volume 1,
pages 891–897. IEEE.
Johnson, A. E. and Hebert, M. (1999). Using spin images
for efficient object recognition in cluttered 3D scenes.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 21(5):433–449.
Ke, Y. and Sukthankar, R. (2004). PCA-SIFT: A more
distinctive representation for local image descriptors.
In IEEE Conference on Computer Vision and Pattern
Recognition, volume 2, pages 498–506.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011a). A large-
scale hierarchical multi-view GRB-D object dataset.
In IEEE International Conference on Robotics and
Automation, pages 1817–1824.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011b). A scalable
tree-based approach for joint object and pose recogni-
tion. In Twenty-Fifth Conference on Artificial Intelli-
gence (AAAI).
Mian, A., Bennamoun, M., and Owens, R. (2005). Au-
tomatic correspondence for 3D modeling: An exten-
sive review. International Journal of Shape Modeling,
11(2):253.
Mian, A., Bennamoun, M., and Owens, R. (2006). Three-
dimensional model-based object recognition and seg-
mentation in cluttered scenes. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
28(10):1584–1601.
Mian, A., Bennamoun, M., and Owens, R. (2010). On the
repeatability and quality of keypoints for local feature-
based 3D object retrieval from cluttered scenes. Inter-
national Journal of Computer Vision, 89(2):348–361.
Novatnack, J. and Nishino, K. (2008). Scale-dependent/
invariant local 3D shape descriptors for fully auto-
matic registration of multiple sets of range images. In
10th European Conference on Computer Vision, pages
440–453.
Rusu, R. and Cousins, S. (2011). 3D is here: Point cloud
library (pcl). In 2011 IEEE International Conference
on Robotics and Automation, pages 1–4.
Salti, S., Tombari, F., and Stefano, L. (2011). A perfor-
mance evaluation of 3D keypoint detectors. In Inter-
national Conference on 3D Imaging, Modeling, Pro-
cessing, Visualization and Transmission, pages 236–
243.
Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T.
(2004). The Princeton shape benchmark. In Inter-
national Conference on Shape Modeling Applications,
pages 167–178.
Sun, Y. and Abidi, M. (2001). Surface matching by 3D
point’s fingerprint. In 8th IEEE International Confer-
ence on Computer Vision, volume 2, pages 263–269.
Taati, B. and Greenspan, M. (2011). Local shape descriptor
selection for object recognition in range data. Com-
puter Vision and Image Understanding, 115(5):681–
694.
Tombari, F., Salti, S., and Di Stefano, L. (2010). Unique
signatures of histograms for local surface description.
In European Conference on Computer Vision, pages
356–369.
Williams, J. and Bennamoun, M. (2000). A multiple view
3D registration algorithm with statistical error model-
ing. IEICE Transactions on Information and Systems,
83(8):1662–1670.
Williams, J. and Bennamoun, M. (2001). Simultaneous reg-
istration of multiple corresponding point sets. Com-
puter Vision and Image Understanding, 81(1):117–
142.
TriSI:ADistinctiveLocalSurfaceDescriptorfor3DModelingandObjectRecognition
93
