
Action Recognition by Matching
Clustered Trajectories of Motion Vectors
Michalis Vrigkas
1
, Vasileios Karavasilis
1
, Christophoros Nikou
1
and Ioannis Kakadiaris
2
1
Department of Computer Science, University of Ioannina, Ioannina, Greece
2
Department of Computer Science, University of Houston, Houston, Texas, U.S.A.
Keywords:
Human Action Recognition, Optical Flow, Motion Curves, Gaussian Mixture Modeling (GMM), Clustering,
Longest Common Subsequence.
Abstract:
A framework for action representation and recognition based on the description of an action by time series
of optical flow motion features is presented. In the learning step, the motion curves representing each action
are clustered using Gaussian mixture modeling (GMM). In the recognition step, the optical flow curves of
a probe sequence are also clustered using a GMM and the probe curves are matched to the learned curves
using a non-metric similarity function based on the longest common subsequence which is robust to noise and
provides an intuitive notion of similarity between trajectories. Finally, the probe sequence is categorized to
the learned action with the maximum similarity using a nearest neighbor classification scheme. Experimental
results on common action databases demonstrate the effectiveness of the proposed method.
1 INTRODUCTION
Action recognition is a preponderantand difficult task
in computer vision. Many applications, including
video surveillance systems, human-computer interac-
tion and robotics to human behavior characterization,
require a multiple activity recognition system.
The problem of categorizing a human action re-
mains a challenging task that has attracted much re-
search effort in the recent years. The surveys in
(Aggarwal and Ryoo, 2011) and (Poppe, 2010) pro-
vide a good overview of the numerous papers on ac-
tion/activity recognition and analyze the semantics of
human activity categorization. Several feature ex-
traction methods for describing and recognizing hu-
man actions have been proposed (Efros et al., 2003;
Schuldt et al., 2004; Jhuang et al., 2007; Niebles et al.,
2008; Fathi and Mori, 2008). A major family of meth-
ods relies on optical flow which has proven to be an
important cue. In (Efros et al., 2003), human actions
are recognized from low-resolution sports video se-
quences using the nearest neighbor classifier, where
humans are represented by windows of height of 30
pixels. The approach in (Fathi and Mori, 2008) is
based on mid-level motion features, which are also
constructed directly from the optical flow features.
Moreover, Wang and Mori employed motion fea-
tures as inputs to hidden conditional random fields
and support vector machine (SVM) classifiers (Wang
and Mori, 2011). Real time classification and pre-
diction of future actions is proposed in (Morris and
Trivedi, 2011), where an activity vocabulary is learnt
through a three step procedure. Other optical flow-
based methods which gained popularity are presented
in (Lin et al., 2009; Chaudhry et al., 2009).
The classification of a video sequence using local
features in a spatio-temporal environment has been
given much focus. Schuldt et al. represent local
events in a video using space-time features, while an
SVM classifier is used to recognize an action (Schuldt
et al., 2004). In (Gorelick et al., 2007), actions are
considered as 3D space time silhouettes of moving
humans. They take advantage of the Poisson equation
solution to efficiently describe an action by utilizing
spectral clustering between sequences of features and
applying nearest neighbor classification to character-
ize an action. Niebles et al. address the problem of
action recognition by creating a codebook of space-
time interest points (Niebles et al., 2008). A hierar-
chical approach was followed in (Jhuang et al., 2007),
where an input video is analyzed into several feature
descriptors depending on their complexity. The final
classification is performed by a multi-class SVM clas-
sifier. In (Doll´ar et al., 2005), spatio-temporal fea-
tures are proposed based on cuboid descriptors. An
action descriptor of histograms of interest points, re-
112
Vrigkas M., Karavasilis V., Nikou C. and Kakadiaris I..
Action Recognition by Matching Clustered Trajectories of Motion Vectors.
DOI: 10.5220/0004277901120117
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 112-117
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

lying on (Schuldt et al., 2004) was presented in (Yan
and Luo, 2012). Random forests for action represen-
tation have also been attracting widespread interest
for action recognition (Yao et al., 2010). Furthermore,
the key issue of how many frames are required for ac-
tion recognition is addressed in (Schindler and Gool,
2008).
In this paper, we address the problem of human
action recognition by representing an action with a
set of clustered motion trajectories. Motion curves
are generated by optical flow features which are then
clustered using a different Gaussian mixture (Bishop,
2006) for each distinct action. The optical flow curves
of a probe sequence are also clustered using a Gaus-
sian mixture model (GMM) and they are matched to
the learned curves using a similarity function (Vla-
chos et al., 2002) relying on the longest common sub-
sequence (LCSS) between trajectories. The LCSS is
robust to noise and provides an intuitive notion of
similarity between trajectories. Since different actors
perform the same action in different manners and at
different speeds, an advantage of the LCSS similarity
is that it can handle with motion trajectories of varied
lengths.
The main contribution of the paper is twofold. At
first, human motion is represented by a small set of
trajectories which are the mean curves of the mix-
ture components along with their covariance matri-
ces. The complexity of the model is considered low,
as it is determined by the Bayesian Information Cri-
terion (BIC), but any other model selection technique
may be applied. Secondly, the use of the longest com-
mon subsequence index allows input curves of differ-
ent length to be compared reliably.
The rest of the paper is organized as follows: we
represent the extraction of motion trajectories, the
clustering and the curve matching in Section 2. In
Section 3, we report results on the Weizmann (Blank
et al., 2005) and the KTH (Schuldt et al., 2004) action
classification datasets. Finally, conclusions are drawn
in Section 4.
2 ACTION REPRESENTATION
AND RECOGNITION
Our goal is to analyze and interpret different classes
of actions to build a model for human activity cat-
egorization. Given a collection of figure-centric se-
quences, we represent motion templates using optical
flow (Lucas and Kanade, 1981) at each frame. As-
suming that a bounding box can be automatically ob-
tained from the image data, we define a square region
of interest (ROI) around the human. A brief overview
of our approach is depicted in Figure 1. In the train-
ing mode, we assume that the video sequences con-
tain only one actor performing only one action per
frame. However, in the recognition mode, we allow
more than one action per video frame. The optical
flow vectors as well as the motion descriptors (Efros
et al., 2003) for each sequence are computed. These
motion descriptors are collected together to construct
motion curves, which are clustered using a mixture
model to describe a unique action. Then, the motion
curves are clustered and each action is characterized
by a set of clustered motion curves. Action recogni-
tion is performed by matching the clusters of motion
curves of the probe sequence and the clustered curves
in each training sequence.
2.1 Motion Representation
Following the work in (Efros et al., 2003), we com-
pute the motion descriptor for the ROI as a four-
dimensional vector F
i
=
F
+
x
i
,F
−
x
i
,F
+
y
i
,F
−
y
i
∈ R
4
,
where i = 1, ..., N, with N being the number of pixels
in the ROI. Also, the matrix F refers to the blurred,
motion compensated optical flow. We compute the
optical flow F, which has two components, the hori-
zontal F
x
, and the vertical F
y
, at each pixel. It is worth
noting that the horizontal and vertical components of
the optical flow F
x
and F
y
are half-wave rectified into
four non-negative channels F
+
x
,F
−
x
,F
+
y
,F
−
y
, so that
F
x
= F
+
x
−F
−
x
and F
y
= F
+
y
−F
−
y
. In the general case,
optical flow is suffering from noisy measurements and
analyzing data under these circumstances will lead to
unstable results. To handle any motion artifacts due
to camera movements, each half-wave motion com-
pensated flow is blurred with a Gaussian kernel. In
this way, the substantive motion information is pre-
served, while minor variations are discarded. Thus,
any incorrectly computed flows are removed.
2.2 Extraction of Motion Curves
Consider T to be the number of image frames and
C ={c
i
(t)},t ∈ [0, T], is a set of motion curves for the
set of pixels i = 1,...,N of the ROI. Each motion curve
is described as a set of points corresponding to the
optical flow vector extracted in the ROI. Specifically,
we describe the motion at each pixel by the optical
flow vector F
i
=
F
+
x
i
,F
−
x
i
,F
+
y
i
,F
−
y
i
. A set of motion
curves for a specific action is depicted in Figure 1.
Given the set of motion descriptors for all frames, we
construct the motion curves by following their optical
flow components in consecutive frames. If there is
no pixel displacement we consider a zero optical flow
vector displacement for this pixel.
ActionRecognitionbyMatchingClusteredTrajectoriesofMotionVectors
113
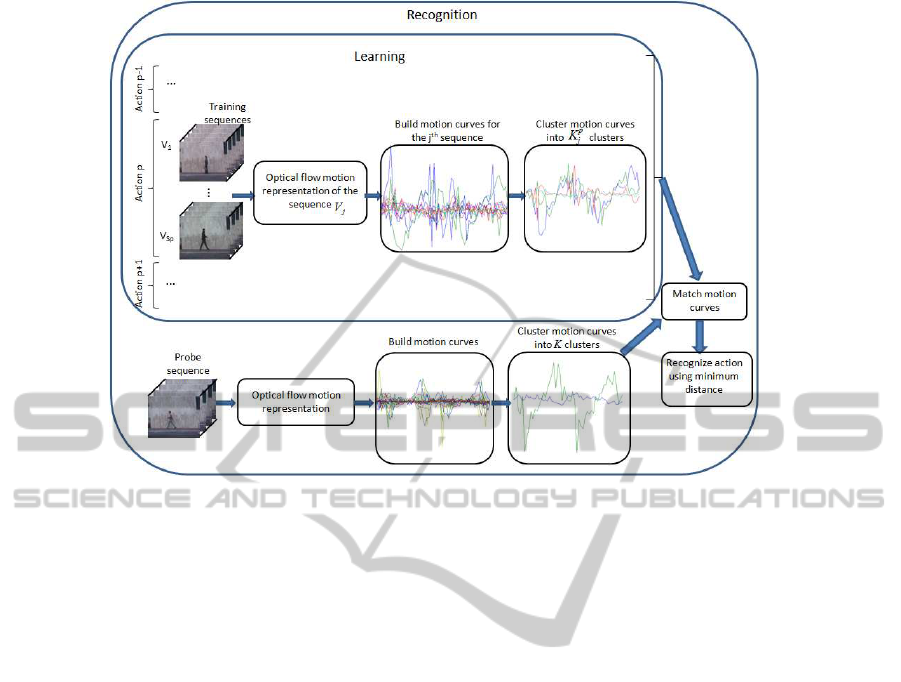
Figure 1: Overview of our approach.
The set of motion curves describes completely
the motion in the ROI. Once the motion curves are
created, pixels and therefore curves that belong to
the background are eliminated. This is accomplished
by discarding curves whose amplitude of the optical
flow vector is below a predefined threshold. In or-
der to establish a correspondence between the motion
curves and the actual motion, we perform clustering
of the motion curves using a Gaussian mixture model.
We estimate the characteristic motion which is repre-
sented by the mean trajectory of each cluster.
2.3 Motion Curves Clustering
A motion curve is considered to be a 2D time sig-
nal c
ji
(t) =
F
x
ji
(t),F
y
ji
(t)
, t ∈ [0, T] where the index
i = 1, . . . , N represents the i
th
pixel, for the j
th
video
sequence in the training set. To efficiently learn hu-
man action categories, each action is represented by
a GMM by clustering the motion curves in every se-
quence of the training set. The p
th
action (p = 1, ..., A)
in the j
th
video sequence (j = 1, . . . ,S
p
) is modeled
by a set of K
p
j
mean curves (learned by the GMM)
denoted by x
p
jk
(t), k = 1, ..., K
p
j
.
The GMM is trained using the Expectation-
Maximization (EM) algorithm (Bishop, 2006), which
provides a solution to the problem of estimating the
model’s parameters. However, the number of mixture
components should be determined. To select the num-
ber of the Gaussians K
p
j
, for the j
th
training sequence,
representing the p
th
action, the Bayesian Information
criterion (BIC) (Bishop, 2006) is used. Thus, when
EM converges the cluster labels of the motion curves
are obtained. This is schematically depicted in Figure
1, where a set of motion trajectories, representing a
certain action (e.g., p), in a video sequence (e.g., la-
beled by j) is clustered by a GMM into K
p
j
= 2 curves
for action representation. Note that, a given action is
generally represented by a varying number of mean
trajectories as the BIC criterion may result in a differ-
ent number of components in different sequences.
2.4 Matching of Motion Curves
Once a new probe video is presented, where we must
recognize the action depicted, the optical flow is com-
puted, motion trajectories are created and clustered,
and they are compared with the learned mean trajecto-
ries of the training set. Recall that human actions are
not uniform sequences in time, since different actors
perform the same action in different manner and at
different speeds. This means that motion curves have
varied lengths. An optimal matching may be per-
formed using dynamic programming which detects
similar pairs of curve segments. The longest com-
mon subsequence (LCSS) (Vlachos et al., 2002) is
robust to noise and provides a similarity measure be-
tween motion trajectories since not all points need to
be matched.
Let c
1
(t), t ∈ [0, T] and c
2
(t
′
), t
′
∈ [0, T
′
] be two
curves of different lengths. Then, we define the affin-
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
114

ity between the two curves as:
α
c
1
(t),c
2
(t
′
)
=
LCSS
c
1
(t),c
2
(t
′
)
min(T,T
′
)
, (1)
where the LCSS
c
1
(t),c
2
(t
′
)
(Eq. (2)) indicates
the quality of the matching between the curves c
1
(t)
and c
2
(t
′
) and measures the number of the matching
points between two curves of different lengths. Note
that the LCSS is a modification of the edit distance
(Theodoridis and Koutroumbas, 2008) and its value is
computed within a constant time window δ and a con-
stant amplitude ε, that control the matching thresh-
olds. The terms c
1
(t)
T
t
and c
2
(t
′
)
T
′
t
′
denote the num-
ber of curve points up to time t and t
′
, accordingly.
The idea is to match segments of curves by perform-
ing time stretching so that segments that lie close to
each other (their temporal coordinates are within δ)
can be matched if their amplitudes differ at most by ε.
When a probe video sequence is presented, its mo-
tion trajectories are clustered using GMMs of various
numbers of components using the EM algorithm. The
BIC criterion is employed to determine the optimal
value of the number of Gaussians K, which represent
the action. Thus, we have a set of K mean trajectories
y
k
, k = 1, . . . , K modeling the probe action.
Recognition of the action present in the probe
video sequence is performed by assigning the probe
action to the action of the labeled sequence which is
most similar. As both the probe sequence y and the j
th
labeled sequence of the p
th
action in the training set
x
p
j
are represented by a number of GMM components,
the overall distance between them is computed by:
d(x
p
j
,y) =
K
p
j
∑
k=1
K
∑
ℓ=1
π
p
jk
π
ℓ
h
1− α
x
p
jk
(t),y
ℓ
(t
′
)
i
, (3)
where π
p
jk
and π
ℓ
are the GMM mixing proportions
for the labeled and probe sequence, respectively, that
is
∑
k
π
p
jk
= 1 and
∑
ℓ
π
ℓ
= 1. The probe sequence y
is categorized with respect to its minimum distance
from an already learned action:
[ j
∗
, p
∗
] = argmin
j, p
d(x
p
j
,y). (4)
3 EXPERIMENTAL RESULTS
We evaluated the proposed method on action recog-
nition by conducting a set of experiments over pub-
licly available datasets. At first we applied the algo-
rithm to the Weizmann human action dataset (Blank
et al., 2005). The Weizmann dataset is a collection
of 90 low-resolution videos, which consists of 10 dif-
ferent actions such as run, walk, skip, jumping jack,
jump forward, jump in place, gallop sideways, wave
with two hands, wave with one hand, and bend, per-
formed by nine different people. The videos were ac-
quired with a static camera and contain uncluttered
background.
To test the proposed method on action recognition
we adopted the leave-one-out scheme. We learned the
model parameters from the videos of eight subjects
and tested the recognition results on the remaining
video set. The procedure was repeated for all sets
of video sequences and the final result is the aver-
age of the individual results. The optimal number of
mixture components K
p
j
for the j
th
video sequence,
j = 1, . . . , S
p
of the p
th
action p = 1, . . . , A is found by
employing the BIC criterion. The value of BIC was
computed for K
p
j
= 1 to 10.
In the recognition step, in our implementation of
the LCSS (2), the constants δ and ε were estimated us-
ing cross validation. Parameter δ, was set to 1% of the
trajectories’ lengths, and parameter ε was determined
as the smallest standard deviation of the two trajecto-
ries to be compared. As shown in Table 1, the average
correct classification of the algorithm on this dataset
is 98.8%. The performances of other state-of-the-art
methods on the same dataset are shown in Table 1.
As it can be observed, we achieve better results with
respect to four out of seven state-of-the-art methods.
However, the proposed method provided only one er-
roneous categorization as one jump-in-place (pjump)
action was wrongly categorized as run. It seems that
in this case the number of Gaussian components K
p
j
computed by the BIC criterion was not optimal. Fig-
ure 2 depicts the confusion matrix for this experiment.
Weizmann database, accuracy = 98.8%
Figure 2: Confusion matrix for the classification results for
the Weizmann dataset for the estimation of the number of
components using the BIC criterion for both the training
and probe sequences.
ActionRecognitionbyMatchingClusteredTrajectoriesofMotionVectors
115

LCSS
c
1
(t),c
2
(t
′
)
=
0, if T = 0 or T
′
= 0,
1+ LCSS
c
1
(t)
T
t
−1
,c
2
(t
′
)
T
′
t
′
−1
, if |c
1
(t) − c
2
(t
′
)| < ε and |T − T
′
| < δ,
max
LCSS
c
1
(t)
T
t
−1
,c
2
(t
′
)
T
′
t
′
, LCSS
c
1
(t)
T
t
,c
2
(t
′
)
T
′
t
′
−1
,otherwise
(2)
Table 1: Recognition accuracy and execution time over the
Weizmann dataset. The results of (Blank et al., 2005; Seo
and Milanfar, 2011; Niebles et al., 2008; Chaudhry et al.,
2009; Lin et al., 2009; Jhuang et al., 2007; Fathi and Mori,
2008) are taken from the original papers.
Method Accuracy (%)
Proposed Method 98 .8
(Blank et al., 2005) 100.0
(Chaudhry et al., 2009) 95 .7
(Fathi and Mori, 2008) 100.0
(Jhuang et al., 2007) 98 .8
(Lin et al., 2009) 100.0
(Niebles et al., 2008) 90 .0
(Seo and Milanfar, 2011) 97 .5
We have further assessed the performance rate of
our method by conducting experiments on the KTH
dataset (Schuldt et al., 2004). This dataset consists of
2391 sequences and contains six types of human ac-
tions such as walking, jogging, running, boxing, hand
waving, and hand clapping. These actions are repeat-
edly performed by 25 different people in four differ-
ent environments: outdoors (s1), outdoors with scale
variation (s2), outdoors with different clothes (s3),
and indoors (s4). The video sequences were acquired
using a static camera and include a uniform back-
ground. The average length of the video sequences
is four seconds, while they were downsampled to the
spatial resolution of 160× 120 pixels.
We tested the action recognition capability of the
proposed method by using a leave-one-out cross vali-
dation approach. Accordingly, we learned the model
from the videos of 24 subjects while we tested the
algorithm on the remaining subject and averaged the
recognition results. The confusion matrix over the
KTH dataset for this leave-one-out approach is de-
picted in Figure 3. We achieved a recognition rate
of 96.71%, which to the best of our knowledge is a
very high performance for this dataset. In addition,
comparison of the proposed method with other state-
of-the-art methods is reported in Table 2. As can be
observed, the proposed method provides the more ac-
curate recognition rates. The proposed method attains
high action classification accuracy as the BIC crite-
rion determines the optimal value of Gaussians K
p
j
for
this dataset.
The average recognition time depends on the
Table 2: Recognition results over the KTH dataset. The
results of (Fathi and Mori, 2008; Jhuang et al., 2007; Lin
et al., 2009; Niebles et al., 2008; Schuldt et al., 2004; Seo
and Milanfar, 2011) are taken from the original papers.
Method Accuracy (%)
Proposed Method 96.71
(Fathi and Mori, 2008) 90.5
(Jhuang et al., 2007) 90.5
(Lin et al., 2009) 95.77
(Niebles et al., 2008) 83.33
(Schuldt et al., 2004) 71.72
(Seo and Milanfar, 2011) 95.1
KTH database, accuracy = 96.71%
Figure 3: Confusion matrix for the classification results for
the KTH dataset for the estimation of the number of compo-
nents using the BIC criterion for both the training and probe
sequences.
value of Gaussians K
p
j
and it is approximately 2 sec
for both datasets, on a standard PC (dual core, 2 GHz
RAM).
4 CONCLUSIONS
In this paper, we presented an action recognition ap-
proach, where actions are represented by a set of mo-
tion curves assumed to be generated by a probabilis-
tic model. The performance of the extracted motion
curves is interpreted by discovering similarities be-
tween the motion trajectories, followed by a classifi-
cation scheme. Although a perfect recognition perfor-
mance is accomplished with a fixed number of Gaus-
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
116

sian mixtures, there are still some open issues in fea-
ture representation. Our next step is to apply this
work to other benchmark databases with richer mo-
tion variations and more information to be modeled
by a Gaussian mixture where more Gaussian compo-
nents would be necessary. Moreover, an extension
of the action classification method is envisioned in
order to integrate it into a complete scheme consist-
ing of motion detection, background subtraction, and
action recognition in natural and cluttered environ-
ments, which is a difficult and more challenging topic.
REFERENCES
Aggarwal, J. K. and Ryoo, M. S. (2011). Human activ-
ity analysis: A review. ACM Compututing Surveys,
43(3):1–43.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer.
Blank, M., Gorelick, L., Shechtman, E., Irani, M., and
Basri, R. (2005). Actions as space-time shapes. In
Proc. 10
th
IEEE International Conference on Com-
puter Vision, pages 1395–1402, Beiging, China.
Chaudhry, R., Ravichandran, A., Hager, G. D., and Vidal,
R. (2009). Histograms of oriented optical flow and
Binet-Cauchy kernels on nonlinear dynamical sys-
tems for the recognition of human actions. In Proc.
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition, pages 1932–1939, Mi-
ami, Florida, USA.
Doll´ar, P., Rabaud, V., Cottrell, G., and Belongie, S. (2005).
Behavior recognition via sparse spatio-temporal fea-
tures. In Proc. 14
th
International Conference on Com-
puter Communications and Networks, pages 65–72,
Beijing, China.
Efros, A. A., Berg, A. C., Mori, G., and Malik, J. (2003).
Recognizing action at a distance. In Proc. 9
th
IEEE
International Conference on Computer Vision, vol-
ume 2, pages 726–733, Nice, France.
Fathi, A. and Mori, G. (2008). Action recognition by learn-
ing mid-level motion features. In Proc. IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition, pages 1–8, Anchorage, Alaska,
USA.
Gorelick, L., Blank, M., Shechtman, E., Irani, M., and
Basri, R. (2007). Actions as space-time shapes. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 29(12):2247–2253.
Jhuang, H., Serre, T., Wolf, L., and Poggio, T. (2007). A
biologically inspired system for action recognition. In
Proc. IEEE International Conference on Computer Vi-
sion, pages 1–8, Rio de Janeiro, Brazil.
Lin, Z., Jiang, Z., and Davis, L. S. (2009). Recognizing ac-
tions by shape-motion prototype trees. In Proc. IEEE
International Conference on Computer Vision, pages
444–451, Miami, Florida, USA.
Lucas, B. D. and Kanade, T. (1981). An iterative image
registration technique with an application to stereo vi-
sion. In Proc. 7
th
International Joint Conference on
Artificial Intelligence, pages 674–679, Nice, France.
Morris, B. T. and Trivedi, M. M. (2011). Trajectory learn-
ing for activity understanding: Unsupervised, multi-
level, and long-term adaptive approach. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
33(11):2287–2301.
Niebles, J. C., Wang, H., and Fei-Fei, L. (2008). Un-
supervised learning of human action categories us-
ing spatial-temporal words. International Journal of
Computer Vision, 79(3):299–318.
Poppe, R. (2010). A survey on vision-based human action
recognition. Image and Vision Computing, 28(6):976–
990.
Schindler, K. and Gool, L. V. (2008). Action snippets: How
many frames does human action recognition require?
pages 1–8, Anchorage, Alaska, USA.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recogniz-
ing human actions: A local SVM approach. In Proc.
17
th
International Conference on Pattern Recognition,
pages 32–36, Cambridge, UK.
Seo, H. J. and Milanfar, P. (2011). Action recognition from
one example. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 33(5):867–882.
Theodoridis, S. and Koutroumbas, K. (2008). Pattern
Recognition. Academic Press, 4th edition.
Vlachos, M., Gunopoulos, D., and Kollios, G. (2002). Dis-
covering similar multidimensional trajectories. In
Proc. 18
th
International Conference on Data Engi-
neering, pages 673–682, San Jose, California, USA.
Wang, Y. and Mori, G. (2011). Hidden part models for
human action recognition: Probabilistic versus max
margin. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 33(7):1310–1323.
Yan, X. and Luo, Y. (2012). Recognizing human actions us-
ing a new descriptor based on spatial-temporal interest
points and weighted-output classifier. Neurocomput-
ing, 87:51–61.
Yao, A., Gall, J., and Gool, L. V. (2010). A Hough
transform-based voting framework for action recog-
nition. In Proc. IEEE Computer Society Conference
on Computer Vision and Pattern Recognition, pages
2061–2068, San Francisco, CA, USA.
ActionRecognitionbyMatchingClusteredTrajectoriesofMotionVectors
117
