
Segmentation of Crystal Defects via Local Analysis of Crystal Distortion
Matt Elsey and Benedikt Wirth
Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, U.S.A.
Keywords:
Segmentation, Crystal Defect, Dislocation, Crystal Distortion, Variational Method, Sparse Curl.
Abstract:
We propose a variational method to simultaneously detect dislocations and grain boundaries in an image of
a crystal as well as the local crystal distortion. To this end we extract a distortion field F from the image
which is nearly curl-free except at dislocations and grain boundaries. The sparsity of the curl is promoted by
an L
1
-regularization of curlF in the employed energy functional. The structure of the functional admits a fast
and parallelizable minimization such that fairly large images can be analyzed in a few minutes.
1 INTRODUCTION
Imagine we are given a large transmission electron
microscopy image or a simulated snapshot of a crys-
talline structure as in Fig. 1 left, and we want to de-
tect all crystal defects, statistically analyze the size
of defect-free regions, and evaluate correlations be-
tween crystal orientations in different regions, per-
haps even for a whole time sequence of such images.
Such tasks are of fundamental importance in materi-
als science and physics to better understand the be-
havior and properties of crystalline materials such as
metals, to validate mathematical models of such ma-
terials, to fit model parameters, or even to optimize
material parameters. Often, the detection of crystal
defects and crystal orientation is accomplished man-
ually, e. g. (Wu and Voorhees, 2012), obviously with
limited feasibility for larger images or sets of data.
We here devise a new automatic crystal segmenta-
tion method which yields the crystal defects, the local
crystal orientation at each point, and the local crys-
tal strain and which can be computed efficiently via
a split Bregman iteration. The algorithm permits par-
allelization on a graphics processing unit (GPU) and
thereby allows for the automatic analysis of images of
a size as in Fig. 1 within few minutes.
We here restrict ourselves to two spatial dimen-
sions which is sufficient for the classical application
of examining microscope images. A generalization to
three dimensions is straightforward.
The two subsequent sections provide the neces-
sary background on crystal structures and introduce
existing related methods before we present our model
and algorithm in Sec. 2 and 3 as well as some numer-
ical examples and a discussion in Sec. 4 and 5.
1.1 Grain Boundaries and Dislocations
We restrict our discussion to two dimensions. In a per-
fect atomic crystal, atoms are arranged in a Bravais
lattice: the atom positions are given by n
1
a
1
+ n
2
a
2
for two fixed vectors a
1
,a
2
∈ R
2
and all integers
n
1
,n
2
. Real materials form polycrystals, that is, crys-
talline regions (so-called grains) of different orienta-
tions, meeting at grain boundaries (Fig. 2 left). These
grain boundaries are often denoted low or high angle
boundaries, depending on the orientation mismatch
between the adjacent grains.
Another type of crystal defect is a dislocation,
where a line of atoms terminates inside a crystal
(Fig. 2 middle). If we draw a closed curve (a so-
called Burgers circuit) on the perfect lattice and map
it onto the crystal around the dislocation (Fig. 2 right),
a gap remains whose direction and length define the
so-called Burgers vector.
Low angle grain boundaries are typically com-
posed of a sequence of dislocations (see e. g. Fig. 1).
Physicists are interested for instance in how de-
fects move and grain boundaries behave or in how the
grain size distribution evolves over time. To this end
crystal images are often analyzed manually.
1.2 Related Methods
Several efficient approaches for the automatic analy-
sis of crystals do already exist, but they either only ap-
ply to molecular dynamics simulation results or they
only provide a segmentation into different grains but
ignore crystal strains or dislocations.
In (Berkels et al., 2008), the authors perform a
piecewise constant Mumford–Shah segmentation of a
294
Elsey M. and Wirth B..
Segmentation of Crystal Defects via Local Analysis of Crystal Distortion.
DOI: 10.5220/0004281502940302
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 294-302
ISBN: 978-989-8565-47-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
(
(
(
(
(
(
(
(
b
b
b
(
(
(
(
(
(
(
(
b
b
b
(
(
(
(
(
(
(
(
b
b
b
(
(
(
(
(
(
(
(
b
b
b
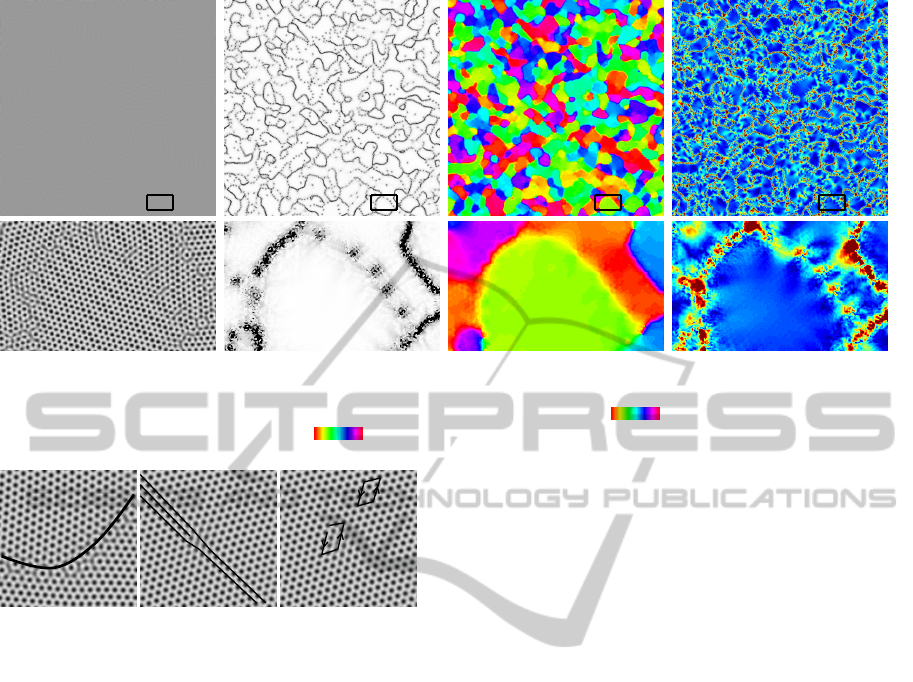
Figure 1: Given a crystal image (left), our method computes a distortion map F : Ω → R
2×2
whose curl magnitude indicates
crystal defects (second image; single spots are dislocations, dotted and continuous lines are low and high angle grain bound-
aries). Polar decomposition of F yields the local crystal orientation (third image, 0
π/3), and dist(F,SO(2)) can be
taken as a measure of crystal strain (right, 0 0.1).
Figure 2: Grain boundary between two grains (left), dislo-
cation with a terminating line of atoms (middle), and same
dislocation enclosed by a curve on the lattice which would
be closed away from the dislocation (right).
crystal image u : Ω → R into disjoint regions Ω
i
⊂ Ω
of constant crystal orientation α
i
∈ [0,2π), using a
Chan–Vese level set approximation. The model can
be augmented by a global deformation φ : Ω → R
2
de-
scribing the elastic crystal deformation in each region.
This approach involves a large number of nonlinearly
coupled degrees of freedom (the orientations α
i
, mul-
tiple level set functions, the deformation φ) and thus
is rather slow; also it concentrates on crystal grains
and ignores the structure of their boundaries or sin-
gle dislocations. Restricting to unstrained grains, the
authors in (Boerdgen et al., 2010) were able to give
a convex formulation of the above Mumford–Shah
segmentation problem based on functional lifting (in-
stead of using the orientation map α : Ω → [0,2π) one
rephrases the functional in terms of 1
α
: Ω × [0, 2π] →
[0,1], 1
α
(x,γ) = 1 if α(x) ≥ γ and 0 else). They also
propose a more efficient version in which the inter-
faces between the Ω
i
are penalized according to the
local angle difference, a method which can be im-
proved further by taking into account the periodic-
ity of the angle (Strekalovskiy and Cremers, 2011).
A GPU implementation of this approach is fast, but
needs lots of memory due to the lifted variable 1
α
.
The method in (Singer and Singer, 2006) assumes
a rather clean crystal image with a perfectly regular,
unstrained grain interior. In that case the grain orien-
tation can be found very rapidly by first convolving
with a wavelet resembling a grid cell and then locally
smoothing out the oscillatory pattern in the convolu-
tion. The resulting grey value indicates the average
mismatch between the crystal and the wavelet and can
thereby be identified with a crystal orientation. How-
ever, for slightly strained crystals this identification is
erroneous; also one cannot distinguish between crys-
tal orientations which equally mismatch the wavelet.
The method seems to incidentally also identify dislo-
cations by a different gray value.
A fast, non-variational dislocation detection
method for three-dimensional molecular dynamics
data is proposed in (Stukowski and Albe, 2010a).
They first identify perfectly crystalline regions by a
nearest neighbor analysis and then find shortest Burg-
ers circuits around the non-perfect regions. This
yields the Burgers vector and location of all dislo-
cations. The method gains in robustness (but can
no longer be used on the fly) by a technique of
sweeping out tubes around the dislocation lines in 3D
(Stukowski and Albe, 2010b). Additionally the au-
thors identify and triangulate grain boundaries which
are not composed of strings of dislocations. A simi-
larly efficient method is introduced in (Begau et al.,
2012). Like our approach, it is based on identify-
ing the curl of the local crystal distortion, which in
a molecular dynamics simulation is readily obtained
from the positions of the nearest neighbor atoms.
In contrast to the above approaches, our method
SegmentationofCrystalDefectsviaLocalAnalysisofCrystalDistortion
295

simultaneously finds dislocations, grain boundaries,
and crystal distortion, just based on a crystal image.
2 VARIATIONAL MODEL
In this section we explain how to identify crystal
defects with curl concentrations of a distortion map
which arises from interpreting an imperfect crystal as
a deformed perfect crystal. We then introduce a sim-
ple energy functional whose minimization leads to the
detection of such curl concentrations.
2.1 Defects as Curl Concentrations
Imagine that a domain Ω ⊂ R
2
is occupied by a per-
fect, unstrained crystal without defects. If this crystal
is deformed according to a smooth deformation φ :
Ω → R
2
, which maps each position x inside the crys-
tal onto a new position φ(x), then the deformed crys-
tal is still defect-free, though it might be strained. A
polycrystal or a crystal with dislocations has a defect-
free, albeit strained, crystal structure away from grain
boundaries and dislocations. In those regions it can
thus be interpreted as a smoothly deformed perfect
crystal. Finding crystal defects hence amounts to the
identification of places where such an interpretation
is not possible. How to accomplish this task?
In their variational approach (Berkels et al., 2008),
the authors attempt to directly find the global defor-
mation φ together with a segmentation of the crys-
tal into different regions across whose boundaries φ
is discontinuous. These boundaries can then be in-
terpreted as grain boundaries, separating defect-free
crystal regions from each other. However, searching
a joint global segmentation and global deformation is
a highly nonlinear problem which makes the method
rather slow. Instead, it would be advantageous to
identify crystal defects based only on the local crystal
structure.
Assume, at each point x inside the crystal we know
the local crystal distortion, that is, the local amount
of rotation, stretching, and shearing (as compared to
an unstrained perfect crystal). This distortion can be
described by a linear map F(x) ∈ R
2×2
. In case of
a smoothly deformed perfect crystal, F : Ω → R
2×2
is given by the gradient of the crystal deformation φ,
F = ∇φ
T
= (∇φ
1
,∇φ
2
)
T
. In order to identify places
where the crystal cannot be described via a smooth
deformation of an unstrained perfect crystal, we now
have to find those regions where F cannot be inter-
preted as the gradient of a deformation, that is, where
F is not conservative. It is well-known that a tensor
Figure 3: Photograph of a synthetic reptile skin (courtesy
http://www.stoff4you.de ) and detected regions of curl con-
centration encoded by color (inset), showing various dislo-
cations.
field F is conservative if and only if it is curl-free,
curlF = (∂
x
F
12
− ∂
y
F
11
,∂
x
F
22
− ∂
y
F
21
) = 0.
The curl-free regions thus represent the defect-free in-
terior of crystal grains, while grain boundaries and
dislocations are characterized by nonzero curlF.
In particular, if the boundary between two grains
is sharp, F is simply discontinuous there and thus
has a measure-valued nonzero curl concentrated along
the boundary, while real crystals typically exhibit a
thin transition region across which the nonzero curl is
spread out. Likewise, the curl of F at a dislocation
behaves like a δ-peak. Its strength
R
curlF dx can be
computed via a line integral around the dislocation,
Z
B
curlF(x)dx =
Z
∂B
Fn
⊥
dx ,
where B is a ball around the dislocation and n
⊥
its
unit outward normal rotated counterclockwise by
π
2
.
The integrand describes how the curve ∂B is locally
stretched by the distortion F, and a nonzero integral
value shows that if one traces the distorted curve one
does not arrive at the starting point, but under- or over-
shoots according to the dislocation’s Burgers vector.
Indeed,
R
∂B
Fn
⊥
dx has the interpretation of the vector
spanning the gap in Fig. 2 right.
Fig. 3 shows the curl concentrations in the scales
pattern of a synthetic reptile skin. These are clearly
located in places where an additional row of scales
squeezes in between two rows. As discussed above,
the shown direction of the curl is related to the Burg-
ers vector and indicates the direction in which the ad-
ditional row of scales is inserted. A red dot for in-
stance implies that
R
∂B
Fn
⊥
dx points upwards, thus
there is vertical dilation left and compression right of
the dislocation so that additional scales are inserted
left of it.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
296

2.2 Variational Curl Segmentation
Given an image u : Ω → R or some other measure-
ment of a crystal structure, we would like to extract
the distortion field F : Ω → R
2×2
, which we expect
to have sparse curl, concentrated at dislocations and
grain boundaries.
We shall follow the usual paradigm in variational
image processing and devise an energy functional as
the sum of a fidelity or fitting term E
fit
[F], which pe-
nalizes a mismatch between F and the given data u,
and a regularization term, which incorporates a priori
knowledge of the structure of F and correspondingly
regularizes F in the case of noisy input data. For regu-
larization we propose the L
1
(Ω)-norm of curlF since
the L
1
-norm is expected to promote sparseness. Thus
we arrive at an energy of the form
E
fit
[F] + ω
1
kcurlFk
1
for some positive weight ω
1
. As for the fitting term,
we restrict ourselves to images u as input data, in
which case we can use the term proposed in (Boerd-
gen et al., 2010),
E
fit
[F] =
Z
Ω
∑
k
(u(x + F(x)v
k
) − u(x))
2
dx , (1)
where v
1
,...,v
K
∈ R
2
represent a stencil of lattice
vectors such that in an image u of a perfect refer-
ence crystal we have u(x + v
k
) = u(x) for all x and
k = 1,. . . , K. The stencil elements v
k
can for instance
be chosen to agree with the K-fold rotational symme-
try of the crystal by
v
k
= `(cos(
2πk
K
),sin(
2πk
K
))
T
,
where ` represents the lattice spacing or characteristic
period of the input image. In the case of a hexagonal
crystal as in Fig. 1 we have K = 6.
Unfortunately, from an analytical viewpoint, the
regularization kcurlFk
1
in combination with a non-
convex fitting term does not provide sufficient com-
pactness to ensure existence of energy-minimizing
tensor fields F, even away from crystal defects, where
a classical minimizer would be expected. Also, exper-
imental results are improved by an additional smooth-
ing term so that for our crystal segmentation problem
we finally choose to minimize the energy
E[F] = E
fit
[F] + ω
1
kcurlFk
1
+ ω
2
k∇Fk
2
2
(2)
with weights ω
1
,ω
2
> 0. For images with gray
values between 0 and 255, the choice (ω
1
,ω
2
) =
(4000`,8000`) seems to generally yield satisfactory
results.
3 MINIMIZATION ALGORITHM
Here we describe the algorithm used to segment im-
ages based on the energy (2). We begin by describ-
ing some of the properties of the model and make
the observation that we seek a local minimizer of (2).
For this reason, a good initial guess for F is required.
We propose one simple technique for initializing F.
Then we discuss the split Bregman formulation of
(Goldstein and Osher, 2009) for problems with L
1
-
type structure and indicate how we apply it to the pro-
posed segmentation model.
3.1 Initialization of F as Rotations
The fitting term (1) makes the variational energy (2)
nonconvex. It can be readily seen that the global min-
imizer of (2), F ≡ 0, is not of interest. Instead, we are
interested in finding a local minimizer of (2) which is
close to an appropriately-chosen initial guess F
0
.
Two observations guide our choice of F
0
: The im-
ages of interest consist of large defect-free, perfectly
crystalline regions, and in those regions the local crys-
tal distortion can be very well described by a mere
rotation.
We choose F
0
(x) at each x ∈ Ω to be the rotation
matrix
F
0
(x) =
cos(α(x)) −sin(α(x))
sin(α(x)) cos(α(x))
=: R
α(x)
,
paramaterized by the angle α(x) which approximately
minimizes (1). To this end we consider a discrete
set of p angles, α
j
=
2π j
K p
with j = 0,. . . , p − 1.
At each pixel x we now identify that rotation R
α
j
which minimizes the integrand of (1) and either set
F
0
(x) = R
α
j
or F
0
(x) = R
α
∗
where α
∗
minimizes the
quadratic interpolation of
∑
k
(u(x + R
α
v
k
) − u(x))
2
at
α = α
j
,α
j±1
(the subscript ( j ± 1) is to be interpreted
mod p). In practice, we find it sufficient to choose
p ∼ 24/K.
3.2 L
1
-Type Minimization
The split Bregman formulation of (Goldstein and Os-
her, 2009) applies the Bregman iteration idea pro-
posed in (Bregman, 1967) and popularized by (Osher
et al., 2005) to a convex energy composed of both L
1
-
and L
2
-type terms. The idea is to introduce a new
variable ψ which corresponds to the L
1
-type term and
then to add the appropriate constraint term to enforce
this correspondence. Suppose E
c
[v] = kζ[v]k
1
+ H[v],
with both kζ[v]k
1
and H[v] convex. This approach ad-
vocates solving
min
v,ψ
kψk
1
+ H[v] subject to ζ[v] = ψ
SegmentationofCrystalDefectsviaLocalAnalysisofCrystalDistortion
297

via Bregman iteration, which is in this context given
by
{v
k+1
,ψ
k+1
}=argmin
v,ψ
kψk
1
+H[v]+λkψ−ζ[v]−b
k
k
2
2
, (3)
b
k+1
= b
k
− ψ
k+1
+ ζ[v
k+1
]. (4)
The split Bregman simplification is to perform alter-
nating minimization on v
k+1
and ψ
k+1
, which allows
for v
k+1
to depend only on L
2
-type terms, and gives
an explicit form for ψ
k+1
:
v
k+1
= argmin
v
H[v]+ λkψ
k
− ζ[v] − b
k
k
2
2
, (5)
ψ
k+1
= shrink(ζ[v
k+1
] + b
k
,
2
λ
), (6)
b
k+1
= b
k
− ψ
k+1
+ ζ[v
k+1
], (7)
with
shrink(z,ω) :=
z
|z|
max(|z| − ω,0).
Theorems proven in (Osher et al., 2005) and
(Goldstein and Osher, 2009) guarantee that if the min-
imization problem (3) can be solved exactly, a mini-
mizer of kψk
1
+H[v] is found which satisfies the con-
straint ψ = ζ[v], i. e. one which solves the original
minimization problem. The split Bregman simplifi-
cation suggests that a single alternating minimization
step for v
k+1
and ψ
k+1
is taken to approximate (3),
however very good results and fast convergence are
still observed in practice. The advantage is that the
original energy, which had both L
1
- and L
2
-character,
has now been reduced to a standard convex L
2
mini-
mization problem to advance v and to a pointwise and
explicitly known update in the new variable ψ.
The minimization problem considered here does
not satisfy the hypothesis of the theorem, as E
fit
[F]
is nonconvex, but the Bregman scheme appears to be
very successful at locating a local minimum of our
energy anyhow. We set
H[F] = E
fit
[F] + ω
2
k∇Fk
2
2
,
ζ[F] = ω
1
curl(F)
and apply the update (5)–(7).
In order to perform the update (5), we apply the
Fletcher–Reeves nonlinear conjugate gradient method
with Armijo stepsize control, as Hessian-based meth-
ods are not expected to (and in practice do not) pro-
vide much benefit for the nonconvex fitting energy E
fit
which also requires interpolation of the image u. We
employed biquadratic interpolation which does not in
general guarantee a continuous interpolation, much
less one which is continuously twice differentiable.
4 NUMERICAL EXPERIMENTS
Fig. 1 already showed a result of our method, applied
to a snapshot from a phase field crystal simulation
Figure 4: Original image and algorithm output for an ini-
tialization of F with rotations in [0,π/3) (left) and rotations
in [π/6,π/2) (right). The top row shows the crystal orien-
tation (0 π/2, obtained via polar decomposition), the
bottom row shows |curlF|. The interpretation of the bottom
left grain as being oriented at 0 rather than the equivalent
π/3 leads to spurious curl.
(PFC, see e. g. (Elder and Grant, 2004)) with hexago-
nal crystals. Our method provides the crystal distor-
tion field F at each pixel from which useful and intu-
itive output can readily be derived: The locations of
high |curlF| represent crystal defects (either disloca-
tions or grain boundaries, second image in Fig. 1), the
rotation R of a polar decomposition F = HR (where
H ∈ R
2×2
is symmetric and R ∈ SO(2)) reveals the
local crystal orientation and thus the extent of crystal
grains (third image), and the distance of F to SO(2)
has the interpretation of an elastic strain (right image).
Together, these pieces of information fully describe
the mesoscopic state of the polycrystal.
In the following sections we provide more exam-
ples of how to deal with large polycrystal images or
crystals of different symmetries, and we report the
typical computational effort.
4.1 Accounting for Point Groups
Especially in images of polycrystals there still re-
mains an issue with the interpretation of our results:
Any two matrices F
1
,F
2
should actually be interpreted
as equivalent if they only differ by the point group
P of the crystal (the set of all rotations and reflec-
tions that leave {v
1
,...,v
K
} invariant). Indeed, if
F
2
= F
1
P for a P ∈ P, then the crystal distorted by
F
2
looks identical to the one distorted by F
1
. Our
model does not automatically account for that fact
and interprets F
1
and F
2
as different distortions, which
can lead to spurious curl accumulations as shown in
Fig. 4. As a remedy, we once initialize F with ro-
tations between [0,
2π
K
) and once with rotations be-
tween [
π
K
,
3π
K
). The result F
1
from the first initializa-
tion typically shows spurious curl along boundaries
of grains at an orientation close to 0 or
2π
K
, while the
second result, F
2
, does so at grain orientations around
π
K
and
3π
K
. We now simply identify regions of spuri-
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
298

Figure 5: After smoothing out the curl of both results in
Fig. 4 (left, middle) we identify the region where the first
has higher values (blue region in right image). In this region
we replace the first output by the second output, yielding the
shown curl (right).
ous curl by comparing |curlF| in both results: in re-
gions where F
1
has a significantly higher curl than F
2
we use F
2
instead of F
1
. In detail, we first smooth
|curlF
1
| and |curlF
2
| (e. g. convolving with a Gaussian
G of roughly two unit cell widths), then we pick the
region where G ∗ |curlF
1
| − G ∗ |curlF
2
| lies above a
certain small threshold (in our simulations 0.01) and
dilate this region by two unit cells. Within this region
we consider F
2
as the correct distortion, outside F
1
(Fig. 5).
4.2 Coarsening Simulations
As a demonstration of this method, we segment a time
series of crystals chosen from a PFC evolution. In
Fig. 6, four time snapshots of the PFC evolution are
considered (left to right). The resulting rotation map,
local volume distortion map (measured as det F − 1),
elastic strain map, and curl magnitude map are dis-
played for each time point (top to bottom). Though
each segmentation is performed independently, it can
be seen that rotations are assigned in a consistent way.
Volume distortion and strain are nonzero near grain
boundaries and dislocations. High magnitude of curl
(|curlF|) is seen to denote grain boundaries and iso-
lated dislocations, which can be easily distinguished
from each other. Note that each dislocation creates a
dipole structure in the volume distortion map, since
the crystal is dilated on one side of the dislocation
and compressed on the other. The orientation of this
dipole can hence also be used as an indicator of the
Burgers vector.
4.3 Strained Crystals
In contrast to the approaches from Sec. 1.2, our
method directly provides the crystal strain, which can
be of interest in particular for the analysis of non-
equilibrated crystals. As a simple example, we per-
formed a PFC simulation, where in regular time inter-
vals we artificially shift a stripe of the simulated ma-
terial horizontally by one pixel, thereby emulating the
effect of a shearing force. The resulting strained crys-
tals are shown in Fig. 7, once for a defect-free crystal
and once for a crystal with three dislocations. The
distribution of elastic strains indicates that the dislo-
cations effectively reduce the strain in the bulk of the
material (while there is a higher peak strain in close
vicinity to the crystal defects).
4.4 Different Crystal Types
The method seems to work robustly on different types
of input images, including real experimental images.
Fig. 8 shows a HRTEM image of a nanocrystalline
palladium thin film, courtesy of Nick Schryvers, from
the work (Wang et al., 2012). The tensor field F is
robustly extracted, even though the coloring varies
across the image, and |curlF| correctly identifies an
isolated dislocation. The crystalline orientation ob-
tained from polar decomposition of F reveals that
three distinct regions separated by twin boundaries
are identified correctly despite no more than 10
◦
dif-
ference in orientation.
In Fig. 3 we used an even more challenging input
image of a reptile skin, whose pattern is rather irreg-
ular compared to an atomic crystal. Nevertheless, us-
ing the six-point stencil of hexagonal symmetry, the
locations as well as the types of the dislocations in
the scales pattern are correctly identified. Note that
the unit cells of the pattern vary strongly in size so
that our initialization of F with pure rotations seems
much less appropriate, yet it obviously still suffices to
achieve the desired local minimizer.
Lattices of different than six-fold rotational sym-
metry can be analyzed using an appropriately adapted
stencil v
1
,...,v
K
. Fig. 9 shows a snapshot of a PFC
simulation with cubic lattice symmetry, for which
an appropriate stencil is given by v
1
= (`,0)
T
, v
2
=
(0,`)
T
, v
3
= (−`,0)
T
, v
4
= (0,−`)
T
(where again,
` is the characteristic spacing). The underlying PFC
model is a modification of the standard PFC model,
presented in (Wu et al., 2010, Sec. VI) and originally
proposed in (Lifshitz and Petrich, 1997) in the context
of the Swift–Hohenberg equation. Isolated disloca-
tions as well as low- and high-angle grain boundaries
are properly identified. The local crystal orientation
indicates that most grains have similar orientations,
with atoms that in this particular simulation tend to
align well with the computational grid.
4.5 Computational Effort
For images as in Fig. 1 we generally found twenty
split Bregman steps to be sufficient, in each of which
we perform five nonlinear conjugate gradient steps
SegmentationofCrystalDefectsviaLocalAnalysisofCrystalDistortion
299
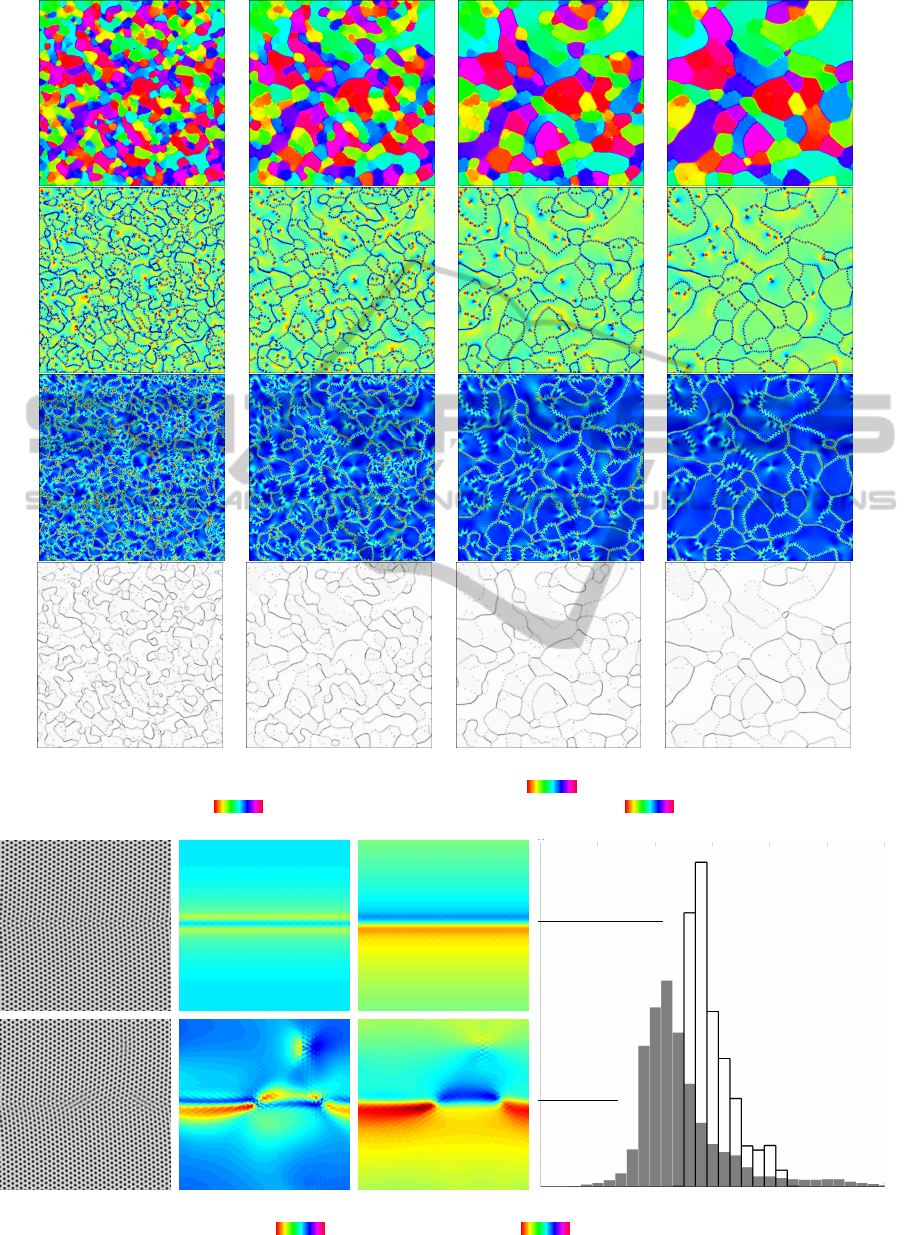
Figure 6: Results of our algorithm applied to different snapshots of a phase field crystal (PFC) coarsening simulation. From
top to bottom we show the time evolution of local crystal orientation (0 π/3), local volume distortion of the crystal
measured as detF − 1 (−0.05 0.05), elastic strain measured as dist(F,SO(2)) (0 0.05), and |curlF|.
0.0 0.5 1.0
-
-
Figure 7: PFC simulation of a sheared crystal without (top) and with (bottom) defects, showing the crystal image (left), the
elastic strain dist(F,SO(2)) (middle, 0 0.15), and F
12
(right, −0.2 0.2). The rightmost graph shows a histogram
of dist(F, SO(2)). The crystal with defects has a higher peak strain, but lower overall strain.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
300

Figure 8: HRTEM image of a nanocrystalline palladium
thin film, from (Wang et al., 2012), detected regions of
curl concentration showing an isolated dislocation, and
the crystal orientation obtained from polar decomposition
(8
◦
18
◦
) showing two twin boundaries.
Table 1: Rounded computation times of GPU implementa-
tion in Matlab for image in Fig. 1 and segments thereof.
image total split NCG inter-
size time Bregman descent polation
2048
2
380 s 312 s 296 s 160 s
1024
2
140 s 108 s 104 s 56 s
512
2
88 s 66 s 62 s 34 s
256
2
68 s 48 s 46 s 26 s
128
2
58 s 40 s 38 s 20 s
for (5). The code is implemented in Matlab, using
the included basic GPU support. Computation times
on a Tesla S10 GPU are displayed in Tab. 1 for dif-
ferent image sizes. For an image with 2048
2
pix-
els, the minimization takes slightly above six minutes
of which the net time inside the split Bregman iter-
ation (without screen output of the energy values) is
roughly 82%. Most of the iteration time is spent in
the nonlinear conjugate gradient steps which in turn
spend more than half of their time interpolating the
image u to evaluate the fitting energy and its gradient.
We observe a strongly sublinear scaling with image
size due to the high GPU parallelization.
Q
Q
Q
Q
Q
Q
Figure 9: Results of our algorithm applied to microstruc-
ture with cubic symmetry. We show the local crystal orien-
tation (0 π/2, top left), local volume distortion of the
crystal measured as det F −1 (−0.05
0.05, top right),
elastic strain measured as dist(F,SO(2)) (0 0.05,
middle left), |curlF| (middle right), a zoom-in on the mi-
crostructure (bottom left), and a zoom in on |curlF| (bottom
right).
The bottleneck seems to lie in the evaluation of
u(x + F(x)v
k
) at each pixel x and for each stencil vec-
tor v
k
(computation times are reported for a six-point
stencil). This image interpolation requires almost un-
structured memory access which without code opti-
mization is not very efficient on a GPU. Nevertheless
a speedup can be expected from a non-Matlab imple-
mentation tailored to the GPU architecture.
5 DISCUSSION
The proposed model is an efficient tool for the
mesoscale analysis of polycrystals, an important task
in materials science. It can analyze fairly large images
in reasonable time, providing information about de-
fect locations and local crystal distortion, from which
different types of statistical data can readily be de-
SegmentationofCrystalDefectsviaLocalAnalysisofCrystalDistortion
301

rived. However, the simple Matlab implementation is
limited in its applicability to image sizes up to around
2000
2
pixels, which can resolve roughly 5·10
4
atoms.
With a tailored GPU implementation, this limit could
probably be pushed back considerably.
Note that in some cases simpler methods are avail-
able. If the atom positions do not have to be ex-
tracted from images, but are known for instance from
a molecular dynamics simulation, then the faster non-
variational methods from Sec. 1.2 can be employed.
The advantage of our approach over these methods
lies in the higher generality of the input data. Also,
for images from phase field crystal (PFC) simula-
tions, the PFC energy density already identifies de-
fect locations (but not the local distortion) quite well
for a range of model parameters. Furthermore, even
though the local crystal orientation does indicate grain
regions and can easily be obtained from our results,
our method does not provide a sharp image segmen-
tation into grains. The segmentation methods from
Sec. 1.2 are better suited for such a purpose, however,
they necessarily ignore single dislocations and details
of the grain boundary structure. Overall, our method
robustly yields more detailed and versatile informa-
tion of the mesoscopic crystal structure (such as local
strain or dislocation character) than previously exist-
ing methods, and it does so much faster than methods
that try to extract a slightly lower level of detail from
similarly general input data.
Finally, let us mention that our model is noncon-
vex and thus requires a sufficiently good initialization
before minimization (which can be obtained at low
cost in most cases). Also, the nonconvexity implies
that the analytical convergence results for the split
Bregman method cannot be relied on. Furthermore,
a better mathematical understanding of the mutual in-
fluence and relative importance between the curl reg-
ularization and the smoothing of the distortion field
might help to further improve the algorithm.
ACKNOWLEDGEMENTS
The authors thank Bob Kohn for continual advice and
suggestions throughout the preparation of this work.
ME and BW gratefully acknowledge the support of
NSF grant OISE–0967140 and a Courant Instructor-
ship, respectively.
REFERENCES
Begau, C., Hua, J., and Hartmaier, A. (2012). A novel ap-
proach to study dislocation density tensors and lattice
rotation patterns in atomistic simulations. Journal of
the Mechanics and Physics of Solids, 60(4):711–722.
Berkels, B., R
¨
atz, A., Rumpf, M., and Voigt, A. (2008). Ex-
tracting grain boundaries and macroscopic deforma-
tions from images on atomic scale. J. Sci. Comput.,
35(1):1–23.
Boerdgen, M., Berkels, B., Rumpf, M., and Cremers, D.
(2010). Convex relaxation for grain segmentation at
atomic scale. In Fellner, D., editor, VMV 2010 - Vi-
sion, Modeling & Visualization, pages 179–186. Eu-
rographics Association.
Bregman, L. M. (1967). The relaxation method of finding
the common point of convex sets and its application
to the solution of problems in convex programming.
USSR Comput. Math. Math. Phys., 7(2):200–217.
Elder, K. R. and Grant, M. (2004). Modeling elastic and
plastic deformations in nonequilibrium processing us-
ing phase field crystals. Phys. Rev. E, 70:051605.
Goldstein, T. and Osher, S. (2009). The split Bregman
method for L1–regularized problems. SIAM J. Imag.
Sci., 2(2):323–343.
Lifshitz, R. and Petrich, D. M. (1997). Theoretical model
for Faraday waves with multiple-frequency forcing.
Phys. Rev. Lett., 79(7):1261–1264.
Osher, S., Burger, M., Goldfarb, D., Xu, J., and Yin, W.
(2005). An iterative regularization method for total
variation-based image restoration. Multiscale Model.
Simul., 4(2):460–489.
Singer, H. M. and Singer, I. (2006). Analysis and visu-
alization of multiply oriented lattice structures by a
two-dimensional continuous wavelet transform. Phys.
Rev. E, 74:031103.
Strekalovskiy, E. and Cremers, D. (2011). Total varia-
tion for cyclic structures: Convex relaxation and ef-
ficient minimization. In Computer Vision and Pat-
tern Recognition (CVPR), 2011 IEEE Conference on,
pages 1905–1911.
Stukowski, A. and Albe, K. (2010a). Dislocation detec-
tion algorithm for atomistic simulations. Modelling
and Simulation in Materials Science and Engineering,
18(2):025016.
Stukowski, A. and Albe, K. (2010b). Extracting disloca-
tions and non-dislocation crystal defects from atom-
istic simulation data. Modelling and Simulation in
Materials Science and Engineering, 18(8):085001.
Wang, B., Idrissi, H., Galceran, M., Colla, M., Turner,
S., Hui, S., Raskin, J., Pardoen, T., Godet, S., and
Schryvers, D. (2012). Advanced TEM investigation
of the plasticity mechanisms in nancrystalline free-
standing palladium films with nanoscale twins. Int.
J. Plast., 37:140–156.
Wu, K.-A., Adland, A., and Karma, A. (2010). Phase-
field-crystal model for fcc ordering. Phys. Rev. E,
81:061601.
Wu, K.-A. and Voorhees, P. W. (2012). Phase field crys-
tal simulations of nanocrystalline grain growth in two
dimensions. Acta Materialia, 60(1):407–419.
VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications
302
