GAIL: Geometry-aware Automatic Image Localization

Luca Benedetti, Massimiliano Corsini, Matteo Dellepiane, Paolo Cignoni and Roberto Scopigno

Visual Computing Lab, ISTI-CNR, Pisa, Italy

Keywords:

Image-based Localization, 2D/3D Registration.

Abstract:

The access and integration of the massive amount of information, that can be provided by the web, can be of

great help in a number of ﬁelds, including tourism and advertising of artistic sites. A “virtual visit” of a place

can be a valuable experience before, during and after the experience on-site. For this reason, the contribution

from the public could be merged to provide a realistic and immersive visit of known places. We propose an

automatic image localization system, which is able to recognize the site that has been framed, and calibrate

it on a pre-existing 3D representation. The system is characterized by very high accuracy and it is able to

validate, in a completely unsupervised manner, the result of the localization. Given an unlocalized image, the

system selects a relevant set of pre-localized images, performs a Structure from Motion partial reconstruction

of this set and then obtain an accurate camera calibration of the image with respect to the model by minimizing

distances between projections on the model surface of corresponding image features. The accuracy reached is

enough to seamlessly view the input image correctly super-imposed in the 3D scene.

1 INTRODUCTION

Automatic image localization is an active research

ﬁeld in Computer Vision and Computer Graphics,

with many important applications. This has become

especially important given the potentials of all the im-

ages coming from the web community. Traditional lo-

calization solutions, e.g. Global Positioning System

(GPS), may present issues in certain urban areas or

indoor environments, or may not be accurate enough.

Moreover, both the position and the orientation of the

camera could be a valuable source of data. Alterna-

tives, like inertial drift-free systems, are too expen-

sive to be applied on a large scale. In this case, the

only class of solutions realistically feasible today is

the use of image-based localization systems. Many

aspects of the automatic image localization problem

have been independently tackled, and tremendous ad-

vances have been obtained in recent years.

Here, we are interested in the automatic user local-

ization through the use of digital consumer cameras

or smartphones to support information services for

tourists. In particular, we cope with a particular im-

age localization scenario, that, to our knowledge, has

never been faced in literature: exploiting pre-existing

high quality 3D models of the photographs’ environ-

ment for performing an ofﬂine, fully automatic, pre-

cise, unsupervised image localization. We aim to ob-

tain such an accuracy to allow a seamless view im-

mersion into the 3D scene by projecting the photos on

the 3D models. High accuracy allows to re-visualize

the picture of the tourist in PhotoCloud (Brivio et al.,

2012) that is a CG application which shares some sim-

ilarities with Photo Tourism (Snavely et al., 2006).

This is one of the main goal of an ongoing project

related to tourism and valorization of artistic sites.

The proposed system effectively merges solutions

from image retrieval, Structure from Motion and

2D/3D registration. In this context, our contribution

is twofold: an image-based localization algorithm ca-

pable to obtain very high accuracy by exploiting pre-

existing high quality 3D models of the locations of in-

terest, and an unsupervised validation algorithm that

guarantees to present only correct results to the user.

The developed system works by exploiting a dataset

of pre-aligned digital photographs on 3D models of

the locations of interest.

2 RELATED WORK

Image localization is a vast ﬁeld. Here, we present a

brief overview of some of the most relevant publica-

tions.

Morris and Smelyanskiy (Morris and Smelyan-

skiy, 2001) faced the problem of single image calibra-

tion over a 3D surface and the simultaneous surface

Benedetti L., Corsini M., Dellepiane M., Cignoni P. and Scopigno R..

GAIL: Geometry-aware Automatic Image Localization.

DOI: 10.5220/0004281800310040

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 31-40

ISBN: 978-989-8565-48-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

reﬁnement based on additional information given by

the image. The algorithm is based on the extraction

of image salient points (using Harris detector (Har-

ris and Stephens, 1988)) and employs minimization

of an objective function via gradient calculation. The

approach works relatively well only when there is a

good initial estimate of the surface, moreover it is not

scalable.

Shao et al. (Shao et al., 2003) treated the prob-

lem of database-based image recognition, by compar-

ing them to a reference image through the use of lo-

cal salient features that are described independently

of possible afﬁne transformations between them.

Wang et al. (Wang et al., 2004) proposed a so-

lution for the Simultaneous Localization And Track-

ing (SLAM) robotic problem (Smith and Cheeseman,

1986). A database of salient points, extracted from

the robot camera, is used for the localization. SLAM

approaches suffer from the “Kidnap problem”, i.e. the

inability to continue the localization and mapping be-

tween non-contiguous locations.

Cipolla et al. (Cipolla et al., 2004) tried to

solve this by applying wide baseline matching al-

gorithm techniques between a digital photo and a

geo-referenced database. The main limitation of this

approach comes from the manual construction of

the database correspondences between the map and

the photos. Robertson and Cipolla (Robertson and

Cipolla, 2004) proposed an improvement of it by ex-

ploiting the perspective lines relative to the vertical

edges of buildings.

Zhang and Kosecka (Zhang and Kosecka, 2006)

built a prototype for urban localization of images that

relies on a photographic database augmented with

GPS information. The system extracts one or more

reference images and from these localized the input

image.

Paletta et al. (Paletta et al., 2006) deﬁned a speciﬁc

system devoted to the improvement in the descrip-

tion of the images’ salient points, called “informative-

SIFT”.

Gordon and Lowe (Gordon and Lowe, 2006) pro-

posed the ﬁrst work which exploited Structure-from-

Motion (SFM) for precise localization of the input im-

age. This approach provided interesting ideas in later

works (Irschara et al., 2009; Li et al., 2010; Sattler

et al., 2011).

Schindler et al. (Schindler et al., 2007) faced

the problem of localization in very large datasets of

streets’ photographs using a tree data structure that

indexes the salient features for scalability.

Zhu et al. (Zhu et al., 2008) built another system

for large-scale global localization, with very high ac-

curacy thanks to the use of 4 cameras, arranged as two

stereo pairs.

Xiao et al. (Xiao et al., 2008) proposed a method

for the recognition and localization of generic ob-

jects from uncalibrated images. The system includes

an interesting algorithm for simultaneous localiza-

tion of objects and camera positions, which combines

segmentation techniques, example models and voting

techniques. The main purpose of the system is ob-

ject recognition using structural representation in 3D

space.

Irschara et al. (Irschara et al., 2009) proposed a

localization system that effectively exploited image-

based 3D reconstruction. After the reconstruction,

each 3D point is associated to a compressed descrip-

tion of the features of the images incidents therein.

Such descriptions are indexed using a tree-based vo-

cabularies for efﬁcient searching.

Li et al. (Li et al., 2010) proposed another feature-

based approach based on a prioritization scheme. The

priority of a point is related to the number of cameras

from the reconstruction it is visible in. The use of a

reduced set of points of highest priority has several

advantages w.r.t. to using all 3D points. This method,

in terms of the number of images that can be regis-

tered, outperforms the algorithm by Irschara et al.

Recently, Sattler et al. (Sattler et al., 2011) pro-

posed a direct 2D-to-3D matching framework. By

associating 3D points to visual words, they quickly

identify possible correspondences for 2D features

which are then veriﬁed in a linear search. The ﬁnal

2D-to-3D correspondences are then used to localize

the image using N-point pose estimation.

Our work shares some similarities with the meth-

ods of Irschara (Irschara et al., 2009) and Sattler (Sat-

tler et al., 2011). The novelty stands in the use of

a more advanced image retrieval algorithm, the ex-

ploitation of 3D geometric information that is not de-

pendant on the photographic dataset, and the valida-

tion through an unsupervised validation algorithm.

3 GEOMETRY-AWARE

AUTOMATIC IMAGE

LOCALIZATION

Our system deals with two speciﬁc requirements: the

localization hast to be automatic and accurate enough

to allow correct superimposition of the input image on

the 3D model for presentation purposes to the tourists.

There are no strict time constraints.

Our solution combines a state-of-the-art image re-

trieval system, an SFM algorithm and solutions com-

ing from 2D/3D registration to recast the problem in

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

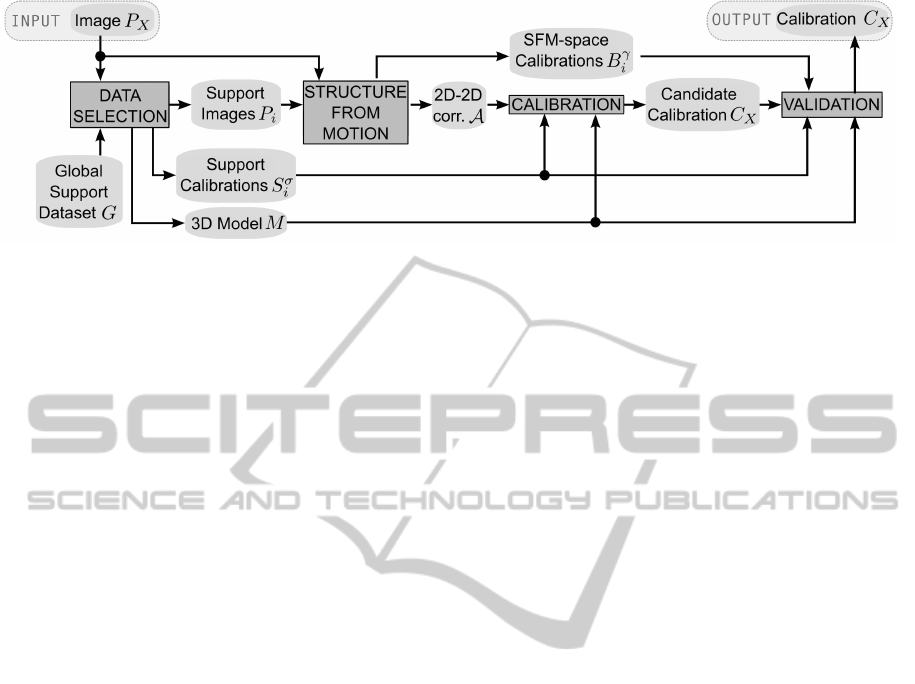
Figure 1: Overview of the algorithm and data ﬂow.

a large-scale 2D/3D calibration problem.

In the following the camera model is deﬁned by

7 parameters: position, orientation, and the focal

length. For the intrinsic parameters we assume that

the skew factor is zero, the principal point is the cen-

ter of the images and the scale factors are assumed to

be known from the resolution and the CCD dimen-

sions.

3.1 Overview

The basic idea of the algorithm is to use an efﬁcient

image retrieval system in order to select relevant and

local information from the support data (implicitly

obtaining a rough approximation of the location), then

use such support data to calibrate the camera. Subse-

quently, the obtained calibration is validated in an un-

supervised way to guarantee high accuracy. The data

ﬂow is shown in Figure 1.

The input is represented by an image P

that needs

to be localized and calibrated. The Data Selection

stage takes advantage of a global support dataset G.

This dataset contains a set of high-resolution 3D mod-

els (one for each location of interest), a set of images

registered on the respective 3D model called support

images and the corresponding camera parameters.

A retrieval image system is used to obtain a lo-

cal subset of G composed by the k images P

which

are most similar to the input image P

. The corre-

sponding support calibration parameters S

and the

3D model M of the location of interest are also ex-

tracted.

The Structure From Motion stage uses P

and the

support images P

to perform a Structure from Motion

(SFM) algorithm to obtain 2D-2D image correspon-

dences A and auxiliary camera calibrations B

(in a

coordinate reference system γ which is generally dif-

ferent from the reference system of the support 3D

model, σ).

Calibration uses the 2D-2D image correspon-

dences (computed at the previous stage), the 3D

model M and the support calibrations S

to calculate

a candidate calibration C

of the input image.

Finally, the Validation stage uses the auxiliary

camera calibrations B

, the 3D model M and the sup-

port calibrations S

to validate C

3.1.1 Creation of the Global Support Dataset

Concerning the creation of G, for each location of

interest a set of images that covers as much as pos-

sible the model surface is acquired through a photo-

graphic campaign. Then, Bundler SFM tool (Snavely

et al., 2006) is used to produce an initial camera cal-

ibration of the images for each location, including a

corresponding point cloud.

Since the results lie on a 3D frame coordinate sys-

tem that is generally different from the coordinates

frame σ of the 3D model, we align the 3D points using

Meshlab (Cignoni et al., 2008). We obtain a similarity

matrix Θ that brings the set of calibrated images (and

the calibrated data) in the σ reference system. The

user can remove bad calibrated images or attempt to

adjust slightly wrong calibrated images by launching

the ﬁne alignment registration algorithm implemented

in Meshlab. If some area of interest is not covered

more images can be added to the set; in this case the

Bundler SFM tool has to be re-launched on the ex-

panded dataset.

3.2 Data Selection Stage

In this stage, Amato and Falchi (Amato and Falchi,

2010) image classiﬁer is used to obtain the subset {P

}

of the global support images. The subset is composed

by the k images which are classiﬁed as the most sim-

ilar to P

. This ensures the scalability of the system

since this image retrieval algorithm is able to work

very efﬁciently for ten of thousands of images. The

algorithm performs a kNN classiﬁcation using local

2D features (SIFT (Lowe, 2004)). We remind the

reader to the original publication for the details of the

algorithm.

GAIL:Geometry-awareAutomaticImageLocalization

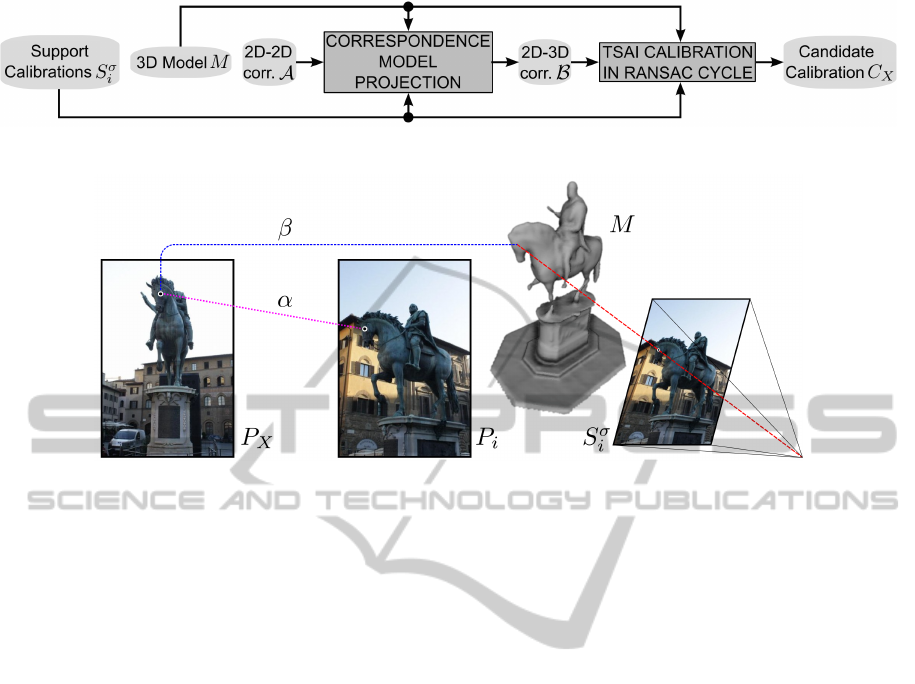
Figure 2: Scheme of the Calibration stage.

Figure 3: Correspondence projection scheme.

We retrieve a list of 15 similar images (P

) that

form the local support images. This list is further

pruned from possible outliers by thresholding over

the similarity metric returned in order to have sup-

port images that shares at least a partial set of features

w.r.t. P

. Then, a voting scheme is used to retrieve

the 3D model of the location from the set of the avail-

able ones. At this point the list is pruned by removing

those images that refer to a different 3D model from

the one chosen by the voting scheme. If the ﬁnal list

is smaller than a minimal set (3 images) the alignment

fails and the image is rejected. The local support im-

ages just represent a rough approximation of the loca-

tion of P

, since they are associated to a portion of a

speciﬁc 3D model M.

3.3 Structure from Motion Stage

The local support images together with P

are given

in input to Bundler (Snavely et al., 2006) to obtain a

set of camera calibrations B

, in a coordinate system

γ, a set of 2D-2D correspondences A between salient

features of the images, and a set of reconstructed 3D

points in γ. A is employed in the Calibration stage,

are used in the Validation stage.

3.4 Calibration Stage

The Calibration stage follows the scheme in Figure 2.

The goal is to obtain a candidate calibration C

on the 3D model M. In order to compute it, we

need a set of 2D-3D correspondences B that matches

points on P

with a set of surface points of the 3D

model. These correspondences are not known in ad-

vance. Nevertheless, we can take advantage of the

2D-2D correspondences A between the local support

images P

and P

, and the corresponding calibrations

, that allow us to project features of P

on the sur-

face of M.

The procedure to build β ∈ B is shown in Figure 3:

we project the feature point in P

on the surface of

M using the camera calibration S

and assign the 3D

point with the corresponding 2D feature point in P

The projection is the intersection between the 3D sur-

face and the ray connecting the feature point in the

image plane with the point of view of the camera. If

no intersection is found, no 2D-3D correspondence is

generated.

During the construction of B, there are many pos-

sible sources of error, such as false positives in A ,

holes or incongruences between the model and the

photographs (i.e. due to movable elements), small er-

rors in camera parameters, etc. Even if multiple 2D-

2D correspondences of the same visual feature in P

are present, we keep all the possible 2D-3D corre-

spondences. This is because our policy is to keep ev-

erything that is potentially correct and to deal with

outliers in the following processing step. After ob-

taining the set of 2D-3D correspondences, we proceed

with the effective calibration.

The calibration step follows a RANSAC (Fischler

and Bolles, 1981) approach, that in each iteration se-

lect a subset of B, making sure to not take dupli-

cates of the same 2D feature on P

. Then, it com-

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

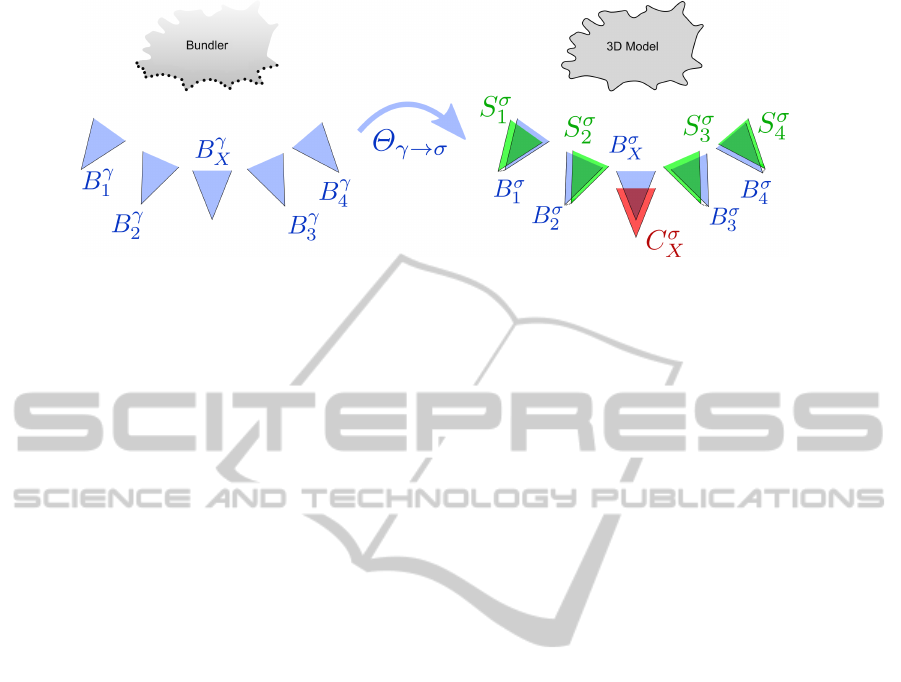
Figure 4: Least Square Mapping scheme.

putes a tentative calibration C

using the well-known

Tsai (Tsai, 1987) algorithm, and computes a projec-

tion error metric to select the “best” calibration. This

approach guarantees robustness with respect to out-

liers in B . It also has a controlled processing time

and avoids “local minima” problems. The RANSAC

cycle is limited in time, because the processing time

of each iteration is variable and depends on the num-

ber of correspondences. The time limit is set to one

minute, but we make sure to do between 250 to 1000

iterations.

In each iteration, we randomly sample a constant

amount of 20 2D-3D correspondences β ∈ B that are

used for the calibration with the Tsai algorithm. Tsai

calibration works with a minimal amount of 9 corre-

spondences but from our experience we found that 20

correspondences are preferable to obtain good results

in presence of noisy data.

After computing the candidate calibration C

, we

measure its quality. For each β ∈ B, we project its 2D

point on the model surface using C

, obtaining the 3D

point ρ. If the projection misses the model surface or

if the distance of ρ from the 3D point in β exceeds a

robust threshold we declare a miss, otherwise a suc-

cess. C

is chosen as the calibration candidate C

there is any success, the misses are less than 10% of

the total, and the average of the distances in successes

is the best one.

4 VALIDATION STAGE

The idea beyond our validation algorithm is to check

the consistency between the estimated calibration C

and the calibration parameters provided by the image-

based reconstruction done with Bundler (see Section

3.3). Measuring the difference between two camera

parameters set is not trivial. We decide to compare

what the two cameras are “seeing” in the scene. To

calculate such consistency measure, we do the follow-

ing two steps:

1. We take the calibration B

given by the image-

based reconstruction for image P

and we map it

in our coordinate frame σ, obtaining B

2. We measure how differently B

and C

view the

same scene comparing two depth maps generated

from these data.

To obtain B

, we exploit relationships between the

support calibrations S

and the calibrations B

com-

puted through Bundler (see Figure 4). The set of

cameras have similar geometrical relationships in the

camera positions, but differences in estimation are

generated, e.g. due to the focal length/view direction

ambiguity.

The estimation of the similarity matrix to obtain

is performed following a RANSAC approach in

order to account for outliers. A subset of the cali-

brations obtained is selected. The difference in scale

is adjusted using the bounding box of the two set of

cameras. Then, the Horn’s method (Horn, 1987) is

applied to estimate a similarity matrix Θ

γ→σ

to trans-

form the coordinate frame from γ to σ.

We evaluate the quality of the similarity matrix by

applying it to all calibrations B

and measuring the

Euclidean distances between the viewpoints with re-

spect to S

. The most accurate Θ

γ→σ

is applied to B

In the second stage, we check the consistency of

and C

, by doing an image-based comparison on

two virtual range maps. We opt for this novel ap-

proach since small changes in camera parameters can

lead to major differences in the framed area, e.g. due

to obstacles.

We proceed by obtaining two low-resolution syn-

thetic range maps R

and R

of the 3D model as seen

by the two cameras obtained. Then, we measure two

errors: the XOR consistency (E

XOR

) of model occlu-

sion versus the background, and the Sum of Squared

Differences (SSD) of depth values (E

SSD

) between R

and R

. The values of R

and R

are normalized to-

gether in the [0 . . . 1] range. Background values are

GAIL:Geometry-awareAutomaticImageLocalization

XOR

∑

0<x<w

0<y<h

RX(R

, R

, x, y)

(1)

SSD

∑

0<x<w

0<y<h

BH(R

, R

, x, y) · (R

(x, y) − R

(x, y))

∑

0<x<w

0<y<h

BH(R

, R

, x, y)

(2)

Almost Correct

XOR

= 0.0115

SSD

= 0.0002

Bad XOR consistency

XOR

= 0.2416,

SSD

= 0.0349

Bad SSD error

XOR

= 0.0339

SSD

= 0.1720

Figure 5: (Left) Input image. (Center) Range map obtained from C

. (Right) Range map obtained from B

set to ∞.

The XOR consistency (Eq. 1) is the percent of pix-

els that in R

are background and in R

are not and

vice-versa, where w and h are the size of the range

maps and RX(R

, R

, x, y) assumes the value 1.0 when

the condition (R

(x, y) = ∞) ⊕ (R

(x, y) = ∞) is true

and 0.0 otherwise. It essentially accounts for different

positions and directions of view.

The SSD error (Eq. 2) measures the dissimilarity

in non-background areas, where BH(R

, R

, x, y) as-

sumes the value 1.0 when both the pixels of R

(x, y)

and R

(x, y) are foreground pixels and 0.0 otherwise.

This measure accounts for errors in position and fo-

cal length, that could lead to the different framing of

objects which are near to the camera.

Examples of the consistency measures are shown

in Figure 5. The second and the third rows show two

calibrations which are incorrect due to different rea-

sons: in the ﬁrst case, the XOR consistency results to

be very high; in the second case, the problem is indi-

cated by the value of the SSD error.

5 EXPERIMENTAL RESULTS

In this section, we will describe and discuss the re-

sults of the experimental evaluation of both the full

image localization algorithm and the validation step.

The global support dataset is composed by images

and 3D models for 2 locations: “Piazza Cavalieri” in

Pisa (Italy) and “Piazza della Signoria” in Florence

(Italy). The “Signoria” location is covered by 304

calibrated images while the “Cavalieri” location by

202 calibrated images. The corresponding 3D models

(485k and 4083k faces respectively) have been ob-

tained through ToF laser scanning, and prepared as

explained in Section 3.1.1.

5.1 Comparison with Previous Work

In order to assess the performance of our system, we

compared it with two recent state-of-the-art works

in image localization (Li et al., 2010; Sattler et al.,

2011). Both these systems were tested using the same

“Dubrovnik” dataset

, which is composed by 6844

images. The authors test their systems by extracting

800 images from the dataset, and try to localize them.

Each test is repeated 10 times.

It was not possible to use the Dubrovnik dataset

in our case, because no 3D model of the city is pro-

vided, However we applied the same testing approach

on our image datasets by attempting to re-align all the

pre-calibrated images 10 times. Results are shown in

Table 1.

Available at http://grail.cs.washington.edu/rome/

dubrovnik/index.html

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

Table 1: Comparison of localization performances between our method and (Li et al., 2010; Sattler et al., 2011).

Tested method average localization # of registered

error (m) images

Li et al (Li et al., 2010) 18.3 94%

Sattler et al (Sattler et al., 2011) 15.7 96%

GAIL (before validation) 3.9 59%

GAIL (after validation) 2.1 26%

Regarding the localization error, our method out-

performs the others. The percentage of acceptance is

lower due to the different goal, accurate calibration,

of our approach with respect to the goal, localization,

of previous work.

Figure 6 shows some examples of the calibra-

tions obtained, we divide the calibration accuracy in:

“high quality” (near pixel-perfect superimposition),

“medium quality” (small misalignments are present),

and “low quality” (severe misalignments with the 3D

models or completely wrong result). It has to be noted

that several of what we refer as “low quality” align-

ments could be accepted as correct by a typical local-

ization system where only the position of the camera

is important and not the orientation as well. Our goal

force us to be more selective to ensure a satisfying

navigation of the localized photographs. The thresh-

olds set in the current system implementation, relative

to the results here reported, allow for “high quality”

calibration.

5.2 Result Evaluation

In order to evaluate the performance of the system, the

validation algorithm in particular, 568 input images

were retrieved from Flickr, in order to cover many

possible cases that the system must face. These im-

ages have been manually inspected before the tests,

in order to have an “a priori” knowledge of which

ones we expect to locate and which ones we expect

to refuse.

This classiﬁcation is based only on the visual in-

spection; we consider “not localizable” images that

are either relative to part not covered by the 3D model,

in very poor lighting condition (i.e. night), or depict-

ing objects that are not strictly part of the scene (e.g. a

bicycle, a cup of coffee). See examples in Figure 7.

After this inspection, we expect to accept 319 (56%)

of the 568 images and to refuse the remaining 249.

Of these 568 images:

• 180 (31.7%) were rejected in the classiﬁcation

step

• 12 (2.1%) were rejected in the reconstruction step

• 146 (25.7%) were rejected in the calibration step.

This means that 230 images (40.5%) were accepted

by calibration. Among these:

• 119 (21.0% of total, 51.7% of selected) failed the

Validation stage.

• 111 (19.5% of total, 48.3% of selected) were val-

idated.

The thresholds used for the validation are E

XOR

≤

0.15 and E

SSD

≤ 0.05.

The method proves to be very selective, since

38.7% of the images which were judged to be accept-

able were discarded during the ﬁrst three stages. On

the other side, only 2 images (0.4% of the total) were

wrongly accepted. This is a key feature for a system

which does not need any human-based validation of

the results.

Moreover, the datasets which were used were not

ideal, both in terms of input data (covering of the sup-

port images, quality of 3D model) and type of envi-

ronment (Piazza della Signoria contains several stat-

ues, so that some images depict details which are hard

to match due to several occlusions).

We expect that the performance could be im-

proved using a more complete (in terms of coverage)

global support dataset.

5.3 Timing

Concerning the processing time of the different stages

of the system, the time to retrieve the local support

set is negligible, since the algorithm by Amato et al.

is designed to deal with millions of images, and the

global support set is usually composed by hundreds

of images. This makes the time to ﬁnd the similar im-

ages practically instantaneous. The calibration stage,

as previously stated, is limited to 1 minute (ensuring

that a certain number of iterations is reached) in the

current implementation, but further optimization to

reduce this processing time can be achieved. Finally,

the validation stage is quite fast, in the order of tenths

of ms on a average-end PC.

5.4 Discussion

The main advantage of the proposed system is that

it is able to work in a completely automatic and un-

supervised way producing very high accurate camera

calibrations for urban context. This implies also a

very accurate localization. The selection of images

GAIL:Geometry-awareAutomaticImageLocalization

Figure 6: Calibration accuracy examples. (1st Row) High quality. (2nd Row) Medium quality. (3rd Row) Low quality.

(a) ETL (b) ETL (c) ETL (d) ETL (e) ETL

(f) ETL (g) ETR (h) ETR (i) ETR (j) ETR

(k) ETR (l) ETR (m) ETR (n) ETR

Figure 7: Examples of images that we expect to locate (ETL): (a) building; (b) statue; (c) partial fac¸ade; (d) small clutter;

(e) moderate clutter; (f) moderate reﬂexes. Examples of images that we expect to refuse (ETR): (g) night time; (h) against

the light; (i) uncovered area (visually similar to covered areas); (j) small detail of statue; (k) ambiguous detail containing

major reﬂection; (l) major clutter; (m) ambiguous detail; (n) panoramic montage. Note that the image (i), that is visually very

similar to a picture of “Piazza della Signoria” in Florence but it is the picture of another plaza, is correctly discarded by the

algorithm.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

Figure 8: Results example. (Center Top) Input image immersed in 3D. (Center Bottom) 3D model view from C

. (Side

Columns) Superimpositions of details.

is very strict, in order to ensure the lowest possible

rate of false positives.

This also gives the possibility to the system to

“train” and increase the robustness, since the success-

fully calibrated images can be added to G in order

to increase the performance of the system itself dur-

ing its use. Moreover, a very high number of pre-

calibrated images could be used, due to the scalability

of the image retrieval algorithm employed.

The main limitation is related to the fact that the

validation step discards a calibration more frequently

for errors in B

than for errors in the Calibration

stage C

. More research in this direction could be of

great interest. Another limitation is that a 3D model

of the scene is needed. Nevertheless, current multi-

view stereo reconstruction techniques are probably

able to provide an accurate enough reconstruction of

the scene.

6 CONCLUSIONS

In this paper we proposed a novel localization algo-

rithm that allows for an accurate 2D/3D registration

of the input image in a large scale context, typically

an urban context.

An unsupervised validation algorithm of the lo-

calization obtained is also proposed. The algorithm

is composed of several stages that take advantage

of a large amount of information that can be ex-

tracted from 2D/3D data: 2D-2D feature correspon-

dences, sparse reconstructions, depth maps from de-

ﬁned points of view.

The performance and the advantages/limitations

of the method are assessed and discussed. The sys-

tem proved to selective, but very accurate and robust.

Thus, all the calibrated images could be directly used

in a photo navigation system without the need of hu-

man validation. Figure 8 shows an example of an im-

age that was perfectly aligned to a complex 3D scene,

with objects of different sizes at different distances

w.r.t. the point of view.

A possible improvement regards optimizing the

system to reduce registration time. Another improve-

ment could be to extract further information from

the image to reduce false negatives. Furthermore,

the calibration could be further reﬁned before vali-

dation. For example, reﬁnement could be obtained

using feature matching (Stamos et al., 2008) or statis-

tical (Corsini et al., 2012) methods.

ACKNOWLEDGEMENTS

This paper has been supported by the Tuscany Region

(POR CREO FESR 2007-2013) in the framework of

the VISITO-Tuscany project and by the EU FP7 IN-

DIGO Innovative Training and Decision Support for

Emergency Operations project (grant no. 242341).

We would also thank Fabio Ganovelli for useful sug-

gestions and insights about this work.

GAIL:Geometry-awareAutomaticImageLocalization

REFERENCES

Amato, G. and Falchi, F. (2010). kNN based image clas-

siﬁcation relying on local feature similarity. In Proc.

SISAP’10, pages 101–108. ACM.

Brivio, P., Benedetti, L., Tarini, M., Ponchio, F., Cignoni, P.,

and Scopigno, R. (2012). Photocloud: interactive re-

mote exploration of large 2D-3D datasets. IEEE Com-

puter Graphics and Applications, pages 1–20.

Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M.,

Ganovelli, F., and Ranzuglia, G. (2008). Meshlab:

an open-source mesh processing tool. In Sixth Euro-

graphics Italian Chapter Conference, pages 129–136.

Cipolla, R., Robertson, D., and Tordoff, B. (2004). Image-

based localisation. In Proc. of 10th Int. Conf. on Vir-

tual Systems and Multimedia, pages 22–29.

Corsini, M., Dellepiane, M., Ganovelli, F., Gherardi, R.,

Fusiello, A., and Scopigno, R. (2012). Fully automatic

registration of image sets on approximate geometry.

International Journal of Computer Vision, pages 1–

21.

Fischler, M. and Bolles, R. (1981). Random sample con-

sensus: a paradigm for model ﬁtting with applications

to image analysis and automated cartography. Com-

munications of the ACM, 24(6):381–395.

Gordon, I. and Lowe, D. (2006). What and where: 3d object

recognition with accurate pose. Toward category-level

object recognition, pages 67–82.

Harris, C. and Stephens, M. (1988). A combined corner and

edge detector. In Alvey vision conference, volume 15.

Manchester, UK.

Horn, B. (1987). Closed-form solution of absolute orienta-

tion using unit quaternions. JOSA A, (April).

Irschara, A., Zach, C., Frahm, J.-M., and Bischof, H.

(2009). From structure-from-motion point clouds to

fast location recognition. In CVPR, pages 2599–2606.

Li, Y., Snavely, N., and Huttenlocher, D. P. (2010). Loca-

tion recognition using prioritized feature matching. In

ECCV, pages 791–804.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Morris, R. and Smelyanskiy, V. (2001). Matching images

to models - camera calibration for 3-d surface recon-

struction. Energy Minimization Methods, pages 105–

117.

Paletta, L., Fritz, G., Seifert, C., Luley, P., and Almer, A.

(2006). A mobile vision service for multimedia tourist

applications in urban environments. 2006 IEEE Intel-

ligent Transportation Systems Conference, pages 566–

572.

Robertson, D. and Cipolla, R. (2004). An image-based sys-

tem for urban navigation. In Proc. BMVC, volume 1,

pages 260–272.

Sattler, T., Leibe, B., and Kobbelt, L. (2011). Fast image-

based localization using direct 2d-to-3d matching. In

IEEE International Conference on Computer Vision

(ICCV), pages 667–674.

Schindler, G., Brown, M., and Szeliski, R. (2007).

City-scale location recognition. In IEEE Confer-

ence on Computer Vision and Pattern Recognition

(CVPR2007), pages 1–7. IEEE Computer Society.

Shao, H., Svoboda, T., Tuytelaars, T., and Van Gool, L.

(2003). HPAT indexing for fast object/scene recogni-

tion based on local appearance. CIVR’03, pages 307–

312.

Smith, R. and Cheeseman, P. (1986). On the representa-

tion and estimation of spatial uncertainty. The inter-

national journal of Robotics Research, 5(4):56.

Snavely, N., Seitz, S. M., and Szeliski, R. (2006). Photo

tourism: exploring photo collections in 3d. In SIG-

GRAPH ’06, pages 835–846.

Stamos, I., Liu, L., Chen, C., Wolberg, G., Yu, G., and

Zokai, S. (2008). Integrating automated range regis-

tration with multiview geometry for the photorealistic

modeling of large-scale scenes. Int. J. Comput. Vision,

78:237–260.

Tsai, R. (1987). A versatile camera calibration technique

for high-accuracy 3d machine vision metrology using

off-the-shelf tv cameras and lenses. IEEE Journal of

Robotics and Automation, 3(4):323–344.

Wang, J., Cipolla, R., and Hongbin, Z. (2004). Image-based

localization and pose recovery using scale invariant

features. pages 711–715.

Xiao, J., Chen, J., Yeung, D.-Y., and Quan, L. (2008). Struc-

turing visual words in 3d for arbitrary-view object lo-

calization. In ECCV ’08, pages 725–737.

Zhang, W. and Kosecka, J. (2006). Image based localization

in urban environments. 3DPVT’06, pages 33–40.

Zhu, Z., Oskiper, T., Samarasekera, S., Kumar, R., and

Sawhney, H. (2008). Real-time global localization

with a pre-built visual landmark database. In CVPR,

pages 1–8.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications