OpenOF

Framework for Sparse Non-linear Least Squares Optimization on a GPU

Cornelius Wefelscheid and Olaf Hellwich

Computer Vision and Remote Sensing, Berlin University of Technology,

Sekr. MAR 6-5, Marchstrasse 23, D-10587, Berlin, Germany

Keywords:

Least Squares Optimization, Bundle Adjustment, Levenberg Marquardt, GPU, Open Source.

Abstract:

In the area of computer vision and robotics non-linear optimization methods have become an important tool.

For instance, all structure from motion approaches apply optimizations such as bundle adjustment (BA). Most

often, the structure of the problem is sparse regarding the functional relations of parameters and measurements.

The sparsity of the system has to be modeled within the optimization in order to achieve good performance.

With OpenOF, a framework is presented, which enables developers to design sparse optimizations regarding

parameters and measurements and utilize the parallel power of a GPU. We demonstrate the universality of our

framework using BA as example. The performance and accuracy is compared to published implementations

for synthetic and real world data.

1 INTRODUCTION

Non-linear least squares optimization is used in many

research ﬁelds where measurements with an under-

lying model are present. Most of the problems con-

sist of hundreds of measurements and are represented

by hundreds of parameters that need to be estimated.

Minimizing the L2-norm between the actual measure-

ment and the estimated value is established by e.g.

solving a least squares system. Usually, as the un-

derlying model is not linear, an iterative method for

solving non-linear least squares needs to be applied.

Such methods linearize the cost function in each it-

eration. The Levenberg-Marquardt (LM) algorithm

has more or less become a standard. It combines

the Gauss-Newton algorithm with the gradient de-

scent approach. In contrast to other approaches, LM

guarantees convergence. The computationally most

intensive part within LM is solving Ax = b in each

iteration. Finding the solution of this normal equa-

tion for a dense matrix has a complexity of O(n

This is not effective when dealing with 100k - 1M

parameters on a standard computer. As most of the

entries in A are zero, a sparse matrix representation

is feasible. Different parametrization for sparse ma-

trices have been used in the past. Most commonly a

coordinate list (COO) is used, which stores for each

entry row, column and value. A more compact stor-

age is represented by the compressed sparse column

(CSC) format. For each entry, the row and the value

are stored in an array. Additionally, the starting in-

dex of each column is saved separately, requiring less

space than COO. The reduction of space between

COO and CSC is neglectable, while the implemen-

tation of efﬁcient algorithms for matrix-vector multi-

plications is important. Since the operations on ma-

trices can be implemented in a highly parallel man-

ner, we believe that multiprocessors, such as GPUs,

are most suitable for this task. The operations within

LM are as well highly parallel, as each cost function

can be evaluated independently. To our knowledge

no library has been developed which can solve gen-

eral sparse non-linear least squares optimizations on

a GPU. Two libraries address this problem in general,

sparseLM (Lourakis, 2010) and g2o (Kummerle et al.,

2011), both operating on a CPU. For solving the nor-

mal equation, they implemented interfaces to various

external sparse math libraries, which provide differ-

ent algorithms for direct solving the normal equation.

In most cases a Cholesky decomposition A = LDL

is applied. In contrast to sparseLM, our approach

works on a GPU (presently only NVIDIA graphics

cards are supported) and uses the high parallel power

of the graphics card to solve the normal equation with

a conjugate gradient (CG) approach, which can also

be chosen as a solver in g2o. The potential of paral-

lelizing CG is the main advantage over a Cholesky

decomposition. Our framework is built upon three

260

Wefelscheid C. and Hellwich O..

OpenOF - Framework for Sparse Non-linear Least Squares Optimization on a GPU.

DOI: 10.5220/0004282702600267

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2013), pages 260-267

ISBN: 978-989-8565-48-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

major libraries, Thrust, CUSP and SymPy. Thrust

enhances the productivity of developers by providing

high level interfaces for massive parallel operations

on multiprocessors. Thrust is integrated in the current

CUDA version 4.2 and supported by NVIDIA. The

framework presented in this paper can directly take

advantage of any improvements. The library CUSP

is based on Thrust and provides developers with rou-

tines for sparse linear algebra. The library SymPy is

an open source library for symbolic mathematics in

Python. The aim of our work is to give scientists a

new tool to test new models in less amount of time.

Using SymPy in our framework enables us to deﬁne

least squares models within a high level scripting lan-

guage. Starting from this, our framework automati-

cally generates C++ code which is compiled, gener-

ating the OpenOF optimization library, which can ei-

ther be called from C++ programmes for efﬁcient use,

or from Python for rapid prototyping. OpenOF will

be published as open source library under the GNU

GPL v3 license.

2 RELATED WORK

Recently, non-linear optimization has gathered a lot

of attention. It has been successfully applied in dif-

ferent areas, e.g. Simultaneous Localization and Map-

ping (SLAM) or BA. We will use BA for evaluating

our framework, as it is a perfect example for a rather

complex but sparse system. Several libraries can be

used to solve BA. The SBA library (Lourakis and Ar-

gyros, 2009) which is used by several research groups

takes advantage of the special structure of the Hessian

matrix to apply the Schur complement for solving the

linear system. Nevertheless it has several drawbacks.

Integrating additional parameters which remain iden-

tical for all measurements (e.g. camera calibration) is

not possible, as the structure would change such that

the Schur complement could not be applied anymore.

With OpenOF, we provide a solution for those prob-

lems.

sparseLM (Lourakis, 2010) provides a software

package which is supposed to be general enough to

handle the same kind of problems as OpenOF does.

However, integrating new models within sparseLM is

time consuming. The performance is slow for prob-

lems with many parameters, as no multithreading is

integrated.

More recently another framework was developed

for similar purposes in graph optimization (Kum-

merle et al., 2011). In g2o, the Jacobian is evaluated

by numerical differentiation which is time consuming

and also degrades the convergence rate. Developers

can choose between direct (Davis, 2006) and itera-

tive solver such as CG. Kummerle et al. (2011) claims

that CG is most often slower than a direct solver. In

our experience direct solvers are more precise. How-

ever utilizing the parallelism of multiprocessors, CG

can be signiﬁcantly faster. Applying a preconditioner

to CG has a large impact on the speed of conver-

gence. g2o uses a block Jacobi preconditioner. For

simplicity we use a diagonal preconditioner which has

been applied successfully for various tasks. A big

advantage of the diagonal preconditioner is, that the

least squares CG is computed directly from the Ja-

cobian without explicitly calculating the Hessian ma-

trix. Several other approaches (Kaess et al., 2011),

which address only a subset of problems, have been

presented previously for least squares optimization.

But so far no library provides the speed, the ease of

use and the generality to become a milestone within

the communities of computer vision or robotics.

3 LEVENBERG-MARQUARDT

LM is regarded as standard for solving non-linear

least squares optimization. It is an iterative approach

which was ﬁrst developed by Levenberg in 1944 and

rediscovered by Marquardt in 1963. The algorithm

determines the local minimum of the sum of least

squares of a multivariant function. An overview of the

family of non-linear least squares optimization tech-

niques can be found in (Madsen et al., 2004). LM

combines a Gauss-Newton method with a steepest de-

scent approach. Given a parameter vector x we want

to ﬁnd a vector x

min

that minimizes the function g(x)

which is deﬁned as the sum of squares of the vector

function f (x).

min

= argmin

g(x) = argmin

∑

i=0

(x)

(1)

As the function is usually not convex, a suitable initial

solution x

needs to be provided. Otherwise, LM will

not converge to the global optimum, but get stuck in

a local minimum, which might be far away from the

optimal solution. In each iteration i, g(x) is approxi-

mated by a second order Tailor series expansion.

˜g(x) = g(x

) + g(x

)

(x − x

) +

g(x

)

(x − x

)

(2)

To ﬁnd the minimum the ﬁrst derivative of Equation

2 is set to zero, resulting in

∂ ˜g(x)

∂x

= g(x

)

+ g(x

)

(x − x

) = 0 . (3)

The ﬁrst order derivative at the point x

can be re-

placed by the transposed Jacobian J

multiplied with

OpenOF-FrameworkforSparseNon-linearLeastSquaresOptimizationonaGPU

261

the residual. The second order derivative is approxi-

mated by the Hessian matrix given as J

J. The pa-

rameter update h = x −x

in each iteration is acquired

by solving the normal equation.

Jh = −J

f (x

) (4)

To include the gradient descent approach, Equation 4

is extended by a damping factor µ. For µ → 0 LM

applies the Gauss-Newton method and for µ → ∞ a

gradient descent step is executed.

J + µI)h = −J

f (x

) (5)

If the update step does not result in a smaller error the

damping factor is increased pushing the parameters

further towards the steepest descent. Else, the update

is performed and the damping factor is reduced. In

cases with a known covariance of the measurements,

Equation 5 is extended to

−1

J + µI)h = −J

−1

f (x

) . (6)

Instead of the Euclidean norm the Mahalanobis dis-

tance is minimized. Solving the normal equation is

the most demanding part of the algorithm. If the nor-

mal matrix has a certain structure, approaches such

as the Schur complement can be applied. Generally,

the normal equation can be solved with a Cholesky

decomposition. Another alternative is an iterative ap-

proach such as CG, which is incorporated in OpenOF.

In the next section, the CG approach will be described

in more detail.

4 CONJUGATE GRADIENT

The CG method is a numerical algorithm for solving

a linear equation system Ax = b with A being sym-

metric positive deﬁnite and x, b ∈ R

. As CG is an

iterative algorithm, there exists a residual vector r

each step k deﬁned as:

= Ax

− b . (7)

CG belongs to the Krylov subspace methods. Krylov

subspace is described by

(A, r

) = span{r

, Ar

, A

, .. . , A

k−1

} . (8)

It is the basis for many iterative algorithms. There

is proof that those methods terminate in at most n

steps. CG is a highly economical method which does

not require much memory or time demanding matrix-

matrix multiplication. While applying CG, a set of

conjugate vectors (p

, p

, ..,p

k−1

, p

) is computed be-

longing to the Krylov subspace. In each step the al-

gorithm computes a vector p

being conjugate to all

previous vectors. A great advantage is that only the

previous vector p

k−1

is needed. Thus, the other vec-

tors can be omitted, thereby saving memory. The al-

gorithm is based on the principle that p

minimizes

the residual over one spanning direction in every it-

eration. CG is initialized with r

= Ax

− b, p

−r

, k = 0. In each iteration a step length α is com-

puted, which minimizes the residual over the current

spanning vector p

= −

(9)

The update of the current approximate solution is

given by

k+1

= x

+ α

(10)

which results in a new residual

k+1

= r

+ α

. (11)

The new conjugate direction is computed from Equa-

tions 12 and 13.

k+1

= −

k+1

(12)

k+1

= r

k+1

+ β

k+1

(13)

Finally k is increased. This procedure is repeated as

long as ||r

|| > ε and k < k

max

. In most cases, only

a few iterations are necessary as the CG method is

used within the iterative LM algorithm. For prove of

convergence and full derivation we refer to (Nocedal

and Wright, 1999).

For practical considerations the explicit computa-

tion of the matrix A = J

J can be omitted. Concate-

nating matrix-vector multiplications for J

and J is

faster and the numerical precision is higher. Such an

approach is known as least squares CG.

5 FRAMEWORK

OpenOF aims at making development cycles faster. It

saves the time of the developer searching for errors by

automatic code generation, but not at the expense of

computational efﬁciency. As we use fast high level

libraries on a GPU, the generated executable gains

performance. The design of the underlying model

assumes different types of objects containing groups

of parameters.These objects are linked by measure-

ments. The objects can be combined in arbitrary ways

(see Fig. 1). Usually, the computation of the Jacobi

matrix is either done by hand, or with the help of a

symbolic toolbox (SymPy, Matlab). Both cases are

error prone. The mistakes easily occure when ei-

ther transferring the code into an optimization library

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

262

Opt. Obj. Type 1 Opt. Obj. Type 3Opt. Obj. Type 2

Meas. Type 1 Meas. Type 2

Figure 1: Optimization objects interact with different mea-

surement types.

such as sparseLM (Lourakis, 2010) or from generat-

ing the derivatives by hand. This step needs to be done

each time small changes are made in the underlying

model. As the cost function usually can be described

in various ways, exploring which modeling of e.g. re-

lations between unknowns and measurements works

best is time consuming. Additionally the convergence

rate highly depends on the chosen model e.g. a con-

vex cost function is most preferable. In OpenOF the

model can be adjusted without further low level pro-

gramming steps, as the necessary code is generated

automatically. The main optimization is designed in

a modular way, enabling developers to easily mod-

ify the optimization algorithm or add new algorithms

while still having the advantage of the high perfor-

mance of a GPU.

An optimization task often comprises thousands

of parameters. Usually several entities have the same

meaning, e.g. (x, y) refer to the coordinate of a point.

Furthermore, these parameters can be grouped to ob-

jects. Within OpenOF all parameters are assigned to

an object. When designing optimization objects, we

distinguish between two different kinds of parame-

ters:

• Variable parameters

• Fixed parameters

The variable parameters will be adjusted within the

optimization. The ﬁxed parameters remain constant

but are necessary to evaluate the cost function. Most

often we end up with a small number of different

types of objects. These objects are linked by so

called measurement types. A measurement represents

a function on which the least squares optimization is

performed. The user deﬁnes the function representing

relations between the different objects. Usually, not

all types of objects are necessary to evaluate a certain

measurement (see Figure 1). Sometimes we have a di-

rect but noisy observation X

obs

, e.g. the position given

from a GPS sensor. In this case we deﬁne a mea-

surement f (X

est

, X

obs

) = X

est

− X

obs

. It is clear that

the observation X

obs

is not allowed to change. This

function can be modeled in two ways in OpenOF. For

the ﬁrst option two different object types are deﬁned,

where the ﬁrst object type has only variable parame-

ters and the second has only ﬁxed parameters. In this

case there are two almost identical object types which

only differ regarding which parameters are allowed to

be changed. It would be more intuitive to have only

one object type which deﬁnes a position with vari-

able parameters. To still be able to ﬁx the parameters

of the observation X

obs

, it is possible in OpenOF to

also ﬁx complete object types within a measurement

function. Getting back to the example, one would de-

ﬁne for the function f , X

est

to be variable and X

obs

to be ﬁxed. This enables researchers to incorporate

constraints such that certain parameters stay close to

the initial values without the need to generate a new

type of object with identical parameters. Being able to

deﬁne an object as constant in one measurement and

variable in another measurement gives much ﬂexibil-

ity for deﬁning an optimization.

Each measurement forms an equation, which is

transformed to a cost function. This cost function

is designed with SymPy. The Jacobian of the cost

function is computed automatically and transformed

to C++ code. Different measurement types as well as

object types combined, result in a graph similar to the

one presented in (Kummerle et al., 2011) (see Figure

1).

By now only the structure of the optimization has

been deﬁned. Next, the optimization needs to be ﬁlled

with actual data. Therefore, a list containing the data

of each type of object is created. A measurement is

deﬁned by the type of measurement as well as the in-

dex pointing to the corresponding data within the data

list.

6 EXAMPLES

We present two examples, ﬁrst the classic BA and

second an alternative BA parametrization inspired

by (Civera et al., 2008) using inverse distances.

BA contains four kinds of optimization objects.

The ﬁrst object is a 3D point parametrized by

a name and its coordinates (pt3:[X,Y,Z]). The

second object type deﬁnes the external camera

parameters (cam:[CX,CY,CZ,q1,q2,q3,q4]) with

the center point and a quaternion representing the

rotation of the camera. Since the same camera

is repeatedly used within one reconstruction, an

extra object for the internal camera parameters

(cam in:[fx,fy,u0,v0,s,k1,k2,k3]) is deﬁned.

This enables us to constrain the optimization. Several

cameras then share the same internal calibration

(focal length, principle point, skew and distortion pa-

rameters). At last a constant object which contains the

pixel measurements (pt2:[x,y]) is speciﬁed. These

parameters remain unchanged within the optimization

OpenOF-FrameworkforSparseNon-linearLeastSquaresOptimizationonaGPU

263

Figure 2: Inverse point parametrization with source camera

and destination camera.

but are generated as the same type of structure. Next,

different measurement types are described. We create

a measurement (quat:[cam],[0]) where the object

is a quaternion enforced to have unit length. The

indices written in the second pair of square brackets

specify the indices of the objects to be optimized.

The next measurement represents the error of the

reprojection in the image with ﬁxed intrinsic parame-

ters (projMetric:[pt2,pt3,cam,cam in],[1,2]).

Only the objects pt3 and cam are part of the

optimization. Adjusting the measurement in a

way that the intrinsic parameters are optimized as

well, the last list is extended by the fourth object

(projRadial:[pt2,pt3,cam,cam in],[1,2,3]).

The user provides the system with information,

closely related to the bracket notation above. Using

OpenOF, it is easy and fast to test different kinds of

parametrizations.

We compare a new BA parametrization with the

one previously described. This new method is called

inverse bundle adjustment (IBA) due to the inverse

depth parametrization (Civera et al., 2008). A 3D

point is no longer described by three parameters, but

with a source camera, a unit vector and an inverse

depth. So the point is linked to the camera of ﬁrst

appearance (see Fig. 2). For the parametrization we

end up with the following list:

• pt3inv:[d][nx,ny,nz]

• cam:[CX,CY,CZ,q1,q2,q3,q4]

• cam in:[fx,fy,u0,v0,s,k1,k2,k3]

• pt2:[x,y]

In this example we distinguish between ﬁx and opti-

mizable parameters. For pt3inv, d is part of the opti-

mization, but nx,ny,nz remain constant. The coordi-

nates (X,Y, Z) of a 3D point are computed according

X =













−1

nq +

C (14)

with q being the quaternion corresponding to the

source camera and C is the camera center. The tilde

above the variable denotes a quaternion representa-

tion of a 3D vector. The described parametrization

has several advantages. The degrees of freedom of the

complete optimization are reduced by 2n with n rep-

resenting the number of points. The part of the state

vector which holds the parameters of the cameras has

the same size, since a camera can be a source and a

destination camera at the same time. At the same time

the amount of measurements is reduced by n. The

measurement in the source camera is neglected. This

might be a disadvantage as more measurements make

the optimization more stable. Regarding the opti-

mization, more important is the ratio between param-

eters and measurements. Assuming that each point is

seen by each camera and n > 7, m > 3, with m be-

ing the number of cameras, the ratio of parameters to

measurements is always smaller for IBA than for BA.

7m + n

2n(m − 1)

7m + 3n

2nm

(15)

For Equation 15 we assumed that the intrinsic

camera parameters are ﬁxed. We investigated a

depth parametrization as well but found the inverse

parametrization to be superior due to a more linear

behavior.

7 RESULTS

For evaluation we compare IBA to BA both computed

with OpenOF. Both methods are evaluated against

simulated data as well as a real world dataset. The

performance is compared against two open source BA

implementations, Simple Sparse Bundle Adjustment

(SSBA) (Zach, 2012) and PBA (Wu et al., 2011). The

latter stands for Parallel Bundle Adjustment imple-

mented for the GPU and CPU. In contrast to SSBA,

PBA uses CG as presented in our approach. We show

that the performance of the specially optimized PBA

is comparable to OpenOF. All evaluations are per-

formed on an Intel i7 with 3.07 GHz, 24 GB RAM

and an NVIDIA GTX 570 graphics card with 2.5

GB memory. For both versions of PBA as well as

for OpenOF we use single precision. In contrast

SSBA runs with double precision. For evaluation we

use synthetic data shown in Fig. 3. The 3D points

are randomly generated and placed on the walls of a

cube. The points are only projected into cameras for

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

264

Figure 3: Setup of points (blue) and cams (red) for the sim-

ulated data.

which the points are directly visible in reality, assum-

ing the cube is not transparent. The cube has a size

of 10x10x10. The cameras are positioned on a cir-

cle with a radius of 8, facing the center of the cube.

The points are projected into a virtual camera with

an image size of 640x480 and a focal length of 1000

measured in pixels. The principle point is assumed to

lie in the center of the image. To simulate structure

from motion approaches, where the initial camera po-

sition is rather a rough estimate, we apply noise to the

camera position. Normally distributed noise of 0.5

pixels is applied to the measurement. Furthermore,

we triangulate new points from the virtual projections

instead of using the original 3D point, resulting in

a more realistic setup. With known positions of the

cameras, we investigate the convergence of the ﬁve

BA implementations stated earlier by continuously

increasing the noise of the camera position. Within

this simulation we use 100 cameras and 1000 points.

The overall estimate of each method is transformed

to the original cameras with a Helmert transforma-

tion. The mean distance error between the estimated

and true camera position is shown in Fig. 4(a) for

different amounts of noise. For each noise level the

mean of several iterations is plotted. Within our test

the GPU implementation of PBA did not converge in

most cases, which is shown in Fig. 4(a). The rea-

son for the failure could not be identiﬁed but we can

exclude a wrong usage as there is only a single line

of code which toggles PBA from a CPU version to

a GPU one. Every other method shows similar preci-

sion for σ < 0.6. For σ > 0.6, IBA shows a better con-

vergence than the other methods due to less degrees

of freedom. Especially the CPU version of PBA most

often did not converge for noise σ > 1.2. The con-

vergence problem of PBA causes also an increasing

time (Fig. 4(b)), while the other approaches stay con-

(a) Precision

(b) Performance

Figure 4: Applying normal distributed noise on the camera

positions (100 cameras).

stant in time. To evaluate the speed of the algorithms,

we run each method with a constant amount of noise

while concomitantly increasing the number of cam-

eras. This reduces the distance between two cameras

and increases the number of projections of one 3D

point. As expected, SSBA, using a direct solver im-

plemented on a CPU, shows the lowest performance.

Regarding this example, the CG approach (OpenOF

and PBA) operates much faster than a direct solver

(see Figs. 5(a) and 5(b)). The GPU version of PBA

cannot be taken into account because it did not con-

verge.

The real world data evaluation is performed on

a dataset with 390 images taken with a Canon EOS

7D camera (see Fig. 6(b)). The pictures were taken

in the American Museum of Natural History within

the scope of a project aiming at the reconstruction

of mammoths. Fig. 6(a) shows the ﬁnal reconstruc-

tion computed with PMVS2 (Furukawa and Ponce,

2010). The path computed with OpenOF is illustrated

in Fig. 6(c). We compare the convergence rates be-

tween SSBA and OpenOF, respectively. PBA is not

OpenOF-FrameworkforSparseNon-linearLeastSquaresOptimizationonaGPU

265

(a) Precision

(b) Performance

Figure 5: Changing the number of cameras with constant

amount of noise on the camera position (σ = 0.5).

included in this part of the evaluation. It has an in-

ternally different error metric for the residuals so that

SSBA and PBA can not be compared at the same time.

As shown in Fig. 7(a), the convergence of SSBA and

OpenOF is similar for BA with respect to the num-

ber of iterations. Regarding the number of iterations

relative to the overall time, the CG approach outper-

forms the direct solver. This success is even larger for

datasets where the amount of overlapping images is

higher, as shown in the synthetic evaluation. The con-

vergence rate of IBA is better than of BA. This might

not hold in any case, but developers are encouraged to

try out different parametrizations to determine the op-

timal solution. Additionally a different parametriza-

tion for the rotation is feasible, e.g. Euler angles.

8 CONCLUSIONS

We present OpenOF, an open source framework for

sparse non-linear least squares optimization. The cost

functions to be optimized are described in a high

(a) Quasi-dense point cloud

(b) Sample image

Figure 6: Three mammoths acquired at the American Mu-

seum of Natural History.

level scripting language. Reducing the implementa-

tion time enables developers to comfortably try dif-

ferent modelings of functions. The estimates are

optimized on a GPU considering the sparse struc-

ture of the model. We showed that the generality

of OpenOF is not accomplished at the expense of

speed. OpenOF can compete with implementations

that are speciﬁcally designed for certain applications.

VISAPP2013-InternationalConferenceonComputerVisionTheoryandApplications

266

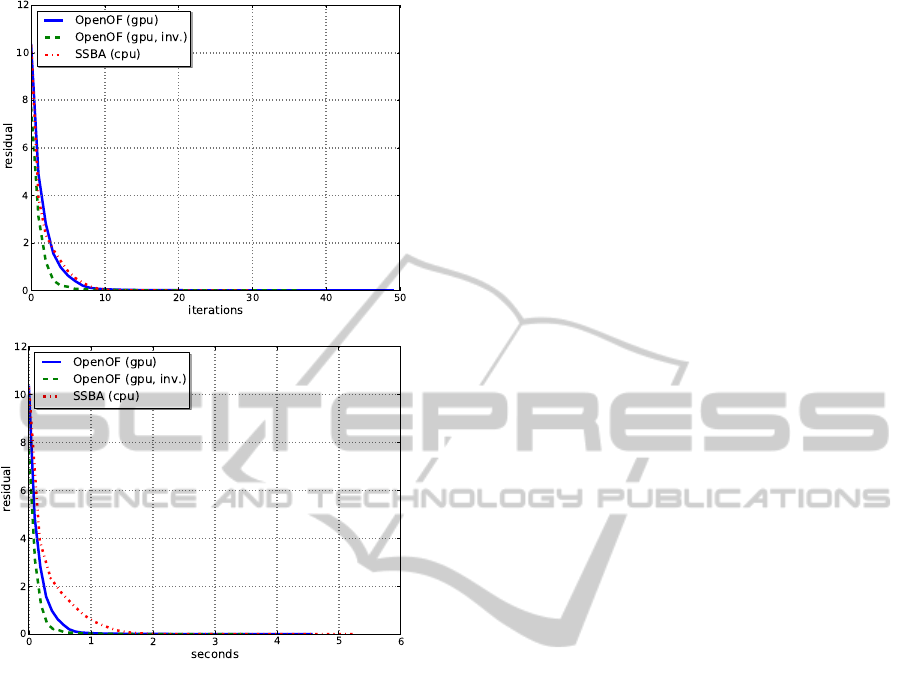
(a) Iterations

(b) Time

Figure 7: Convergence of the mammoth dataset.

OpenOF works successful on BA. A fair comparison

to the GPU version of PBA was not possible since

PBA did not provide reliable results. We will further

investigate why PBA shows just a poor convergence

behavior on our data. With IBA a new parametriza-

tion for BA has been introduced which often converge

for examples in which BA gets stuck in a local min-

imum. As in IBA the reprojection error of a point in

the source camera is zero, IBA probably does not ﬁnd

the overall best solution. In practice we experienced

that IBA still converges for multiple datasets where

BA found a poor solution. In this case the result of

IBA can be further optimized with an additional BA

step.

The main aim of OpenOF is not to be another

BA implementation but to solve much more complex

least squares optimizations problems. Recently a fea-

ture has been added to OpenOF which allows the cost

function to include numerical parts. This is useful for

minimizing pixel differences in multiview stereo ap-

proaches. A set of various robust cost functions such

as Huber or a truncated L2 norm is available as well.

For future releases we want to integrate a CPU ver-

sion especially for developers which does not need

the speed, but want to have the ﬂexibility in their de-

sign of cost functions.

REFERENCES

Civera, J., a.J. Davison, and Montiel, J. (2008). Inverse

Depth Parametrization for Monocular SLAM. IEEE

Transactions on Robotics, 24(5):932–945.

Davis, T. A. (2006). Direct Methods for Sparse Linear

Systems, volume 75 of Fundamentals of Algorithms.

SIAM.

Furukawa, Y. and Ponce, J. (2010). Accurate, dense, and ro-

bust multiview stereopsis. IEEE transactions on pat-

tern analysis and machine intelligence, 32(8):1362–

76.

Kaess, M., Johannsson, H., Roberts, R., Ila, V., Leonard, J.,

and Dellaert, F. (2011). iSAM2: Incremental smooth-

ing and mapping with ﬂuid relinearization and incre-

mental variable reordering. In Robotics and Automa-

tion (ICRA), 2011 IEEE International Conference on,

pages 3281–3288. IEEE.

Kummerle, R., Grisetti, G., Strasdat, H., Konolige, K.,

and Burgard, W. (2011). g2o: A general framework

for graph optimization. In Robotics and Automa-

tion (ICRA), 2011 IEEE International Conference on,

pages 3607–3613. IEEE.

Lourakis, M. (2010). Sparse non-linear least squares op-

timization for geometric vision. Computer Vision -

ECCV 2010, pages 43–56.

Lourakis, M. I. A. and Argyros, A. A. (2009). SBA: A

software package for generic sparse bundle adjust-

ment. ACM Transactions on Mathematical Software,

36(1):1–30.

Madsen, K., Nielsen, H. B., and Tingleff, O. (2004). Meth-

ods for Non-Linear Least Squares Problems (2nd ed.).

Nocedal, J. and Wright, S. J. (1999). Numerical Optimiza-

tion, volume 43 of Springer Series in Operations Re-

search. Springer.

Wu, C., Agarwal, S., Curless, B., and Seitz, S. (2011). Mul-

ticore bundle adjustment. In Computer Vision and Pat-

tern Recognition (CVPR), 2011 IEEE Conference on,

number x, pages 3057–3064. IEEE.

Zach, C. (2012). Sources. http://www.inf.ethz.ch/personal/

chzach/ opensource.

OpenOF-FrameworkforSparseNon-linearLeastSquaresOptimizationonaGPU

267